Provides a magnetic field. The magnetic field of a current-carrying conductor. Changes in the magnetic properties of materials

Magnetic field and its characteristics

Lecture plan:

Magnetic field, its properties and characteristics.

A magnetic field- the form of existence of matter surrounding moving electric charges (conductors with current, permanent magnets).

This name is due to the fact that, as the Danish physicist Hans Oersted discovered in 1820, it has an orienting effect on the magnetic needle. Oersted's experiment: a magnetic needle was placed under a wire with current, rotating on a needle. When the current was turned on, it was installed perpendicular to the wire; when changing the direction of the current, it turned in the opposite direction.

Basic properties magnetic field:

generated by moving electric charges, conductors with current, permanent magnets and an alternating electric field;

acts with force on moving electric charges, conductors with current, magnetized bodies;

an alternating magnetic field generates an alternating electric field.

It follows from Oersted's experience that the magnetic field is directional and must have a vector force characteristic. It is designated and called magnetic induction.

The magnetic field is depicted graphically using magnetic lines of force or lines of magnetic induction. magnetic force lines are called lines along which iron filings or axes of small magnetic arrows are located in a magnetic field. At each point of such a line, the vector is directed tangentially.

The lines of magnetic induction are always closed, which indicates the absence of magnetic charges in nature and the vortex nature of the magnetic field.

Conventionally, they leave the north pole of the magnet and enter the south. The density of the lines is chosen so that the number of lines per unit area perpendicular to the magnetic field is proportional to the magnitude of the magnetic induction.

Magnetic solenoid with current

The direction of the lines is determined by the rule of the right screw. Solenoid - a coil with current, the turns of which are located close to each other, and the diameter of the turn is much less than the length of the coil.

The magnetic field inside the solenoid is uniform. A magnetic field is called homogeneous if the vector is constant at any point.

The magnetic field of a solenoid is similar to the magnetic field of a bar magnet.

FROM

The olenoid with current is an electromagnet.

Experience shows that for a magnetic field, as well as for an electric field, superposition principle: the induction of the magnetic field created by several currents or moving charges is equal to the vector sum of the inductions of the magnetic fields created by each current or charge:

The vector is entered in one of 3 ways:

a) from Ampère's law;

b) by the action of a magnetic field on a loop with current;

c) from the expression for the Lorentz force.

BUT mper experimentally established that the force with which the magnetic field acts on the element of the conductor with current I, located in a magnetic field, is directly proportional to the force

current I and the vector product of the length element and the magnetic induction:

- Ampère's law

H
the direction of the vector can be found according to the general rules of the vector product, from which follows the rule of the left hand: if the palm of the left hand is positioned so that the magnetic lines of force enter it, and 4 outstretched fingers are directed along the current, then the bent thumb will show the direction of the force.

The force acting on a wire of finite length can be found by integrating over the entire length.

For I = const, B=const, F = BIlsin

If  =90 0 , F = BIl

Magnetic field induction- a vector physical quantity numerically equal to the force acting in a uniform magnetic field on a conductor of unit length with unit current, located perpendicular to the magnetic field lines.

1Tl is the induction of a uniform magnetic field, in which a 1m-long conductor with a current of 1A, located perpendicular to the magnetic field lines, is acted upon by a force of 1N.

So far, we have considered macrocurrents flowing in conductors. However, according to Ampere's assumption, in any body there are microscopic currents due to the movement of electrons in atoms. These microscopic molecular currents create their own magnetic field and can turn in the fields of macrocurrents, creating an additional magnetic field in the body. The vector characterizes the resulting magnetic field created by all macro- and microcurrents, i.e. for the same macrocurrent, the vector in different media has different values.

The magnetic field of macrocurrents is described by the magnetic intensity vector .

For a homogeneous isotropic medium

 0 \u003d 410 -7 H / m - magnetic constant,  0 \u003d 410 -7 N / A 2,

 - magnetic permeability of the medium, showing how many times the magnetic field of macrocurrents changes due to the field of microcurrents of the medium.

magnetic flux. Gauss' theorem for magnetic flux.

vector flow(magnetic flux) through the pad dS is called a scalar value equal to

where is the projection onto the direction of the normal to the site;

 - angle between vectors and .

directional surface element,

The vector flux is an algebraic quantity,

if - when leaving the surface;

if - at the entrance to the surface.

The flux of the magnetic induction vector through an arbitrary surface S is equal to

For a uniform magnetic field =const,

1 Wb - magnetic flux passing through a flat surface of 1 m 2 located perpendicular to a uniform magnetic field, the induction of which is equal to 1 T.

The magnetic flux through the surface S is numerically equal to the number of magnetic lines of force crossing the given surface.

Since the lines of magnetic induction are always closed, for a closed surface the number of lines entering the surface (Ф 0), therefore, the total flux of magnetic induction through a closed surface is zero.

- Gauss theorem: the flux of the magnetic induction vector through any closed surface is zero.

This theorem is a mathematical expression of the fact that in nature there are no magnetic charges on which the lines of magnetic induction would begin or end.

Biot-Savart-Laplace law and its application to the calculation of magnetic fields.

The magnetic field of direct currents of various shapes was studied in detail by fr. scientists Biot and Savart. They found that in all cases the magnetic induction at an arbitrary point is proportional to the strength of the current, depends on the shape, dimensions of the conductor, the location of this point in relation to the conductor and on the medium.

The results of these experiments were summarized by fr. mathematician Laplace, who took into account the vector nature of magnetic induction and hypothesized that the induction at each point is, according to the principle of superposition, the vector sum of the inductions of the elementary magnetic fields created by each section of this conductor.

Laplace in 1820 formulated a law, which was called the Biot-Savart-Laplace law: each element of a conductor with current creates a magnetic field, the induction vector of which at some arbitrary point K is determined by the formula:

- Biot-Savart-Laplace law.

It follows from the Biot-Sovar-Laplace law that the direction of the vector coincides with the direction of the cross product. The same direction is given by the rule of the right screw (gimlet).

Given that ,

Conductor element co-directional with current;

Radius vector connecting with point K;

The Biot-Savart-Laplace law is of practical importance, because allows you to find at a given point in space the induction of the magnetic field of the current flowing through the conductor of finite size and arbitrary shape.

For an arbitrary current, such a calculation is a complex mathematical problem. However, if the current distribution has a certain symmetry, then the application of the superposition principle together with the Biot-Savart-Laplace law makes it possible to calculate specific magnetic fields relatively simply.

Let's look at some examples.

A. Magnetic field of a rectilinear conductor with current.

for a conductor of finite length:

for a conductor of infinite length:  1 = 0,  2 = 

B. Magnetic field at the center of the circular current:

=90 0 , sin=1,

Oersted in 1820 experimentally found that the circulation in a closed circuit surrounding a system of macrocurrents is proportional to the algebraic sum of these currents. The coefficient of proportionality depends on the choice of the system of units and in SI is equal to 1.

C
the circulation of a vector is called a closed-loop integral.

This formula is called circulation theorem or total current law:

the circulation of the magnetic field strength vector along an arbitrary closed circuit is equal to the algebraic sum of the macrocurrents (or total current) covered by this circuit. his characteristics In the space surrounding currents and permanent magnets, there is a force field called magnetic. Availability magnetic fields shows up...

On the real structure of the electromagnetic fields and his characteristics propagation in the form of plane waves.

Article >> Physics

ON THE REAL STRUCTURE OF ELECTROMAGNETIC FIELDS And HIS CHARACTERISTICS PROPAGATIONS IN THE FORM OF PLANE WAVES ... other components of a single fields: electromagnetic field with vector components and, electric field with components and magnetic field with components...

Magnetic field, circuits and induction

Abstract >> Physics

... fields). Basic characteristic magnetic fields is his vector force magnetic induction (induction vector magnetic fields). in SI magnetic... with magnetic moment. Magnetic field and his parameters Direction magnetic lines and...

Magnetic field (2)

Abstract >> Physics

Section of conductor AB with current in magnetic field perpendicular his magnetic lines. When shown in the figure ... the value depends only on magnetic fields and can serve his quantitative characteristic. This value is taken...

Magnetic materials (2)

Abstract >> Economics

Materials that interact with magnetic field expressed in his change, as well as in others ... and after the cessation of exposure magnetic fields.one. Main characteristics magnetic materialsThe magnetic properties of materials are characterized by...

For a long time, the magnetic field has raised many questions in humans, but even now it remains a little-known phenomenon. Many scientists tried to study its characteristics and properties, because the benefits and potential of using the field were indisputable facts.

Let's take everything in order. So, how does any magnetic field act and form? That's right, from electric current. And the current, according to physics textbooks, is a stream of charged particles with a direction, isn't it? So, when a current passes through any conductor, a certain kind of matter begins to act around it - a magnetic field. The magnetic field can be created by the current of charged particles or by the magnetic moments of electrons in atoms. Now this field and matter have energy, we see it in electromagnetic forces that can affect the current and its charges. The magnetic field begins to act on the flow of charged particles, and they change the initial direction of motion perpendicular to the field itself.

Another magnetic field can be called electrodynamic, because it is formed near moving particles and affects only moving particles. Well, it is dynamic due to the fact that it has a special structure in rotating bions in a region of space. An ordinary electric moving charge can make them rotate and move. Bions transmit any possible interactions in this region of space. Therefore, the moving charge attracts one pole of all bions and causes them to rotate. Only he can bring them out of a state of rest, nothing else, because other forces will not be able to influence them.

In an electric field are charged particles that move very fast and can travel 300,000 km in just a second. Light has the same speed. There is no magnetic field without an electric charge. This means that the particles are incredibly closely related to each other and exist in a common electromagnetic field. That is, if there are any changes in the magnetic field, then there will be changes in the electric field. This law is also reversed.

We talk a lot about the magnetic field here, but how can you imagine it? We cannot see it with our human naked eye. Moreover, due to the incredibly fast propagation of the field, we do not have time to fix it with the help of various devices. But in order to study something, one must have at least some idea of it. It is also often necessary to depict the magnetic field in diagrams. In order to make it easier to understand it, conditional field lines are drawn. Where did they get them from? They were invented for a reason.

Let's try to see the magnetic field with the help of small metal filings and an ordinary magnet. Let's pour on flat surface these sawdust and introduce them into the action of a magnetic field. Then we will see that they will move, rotate and line up in a pattern or pattern. The resulting image will show the approximate effect of forces in a magnetic field. All forces and, accordingly, lines of force are continuous and closed in this place.

The magnetic needle has similar characteristics and properties to a compass and is used to determine the direction of the lines of force. If it falls into the zone of action of a magnetic field, we can see the direction of action of forces by its north pole. Then we will single out several conclusions from here: the top of an ordinary permanent magnet, from which the lines of force emanate, is designated by the north pole of the magnet. Whereas the south pole denotes the point where the forces are closed. Well, the lines of force inside the magnet are not highlighted in the diagram.

The magnetic field, its properties and characteristics are quite widely used, because in many problems it has to be taken into account and studied. This is the most important phenomenon in the science of physics. More complex things are inextricably linked with it, such as magnetic permeability and induction. To explain all the reasons for the appearance of a magnetic field, one must rely on real scientific facts and confirmations. Otherwise, more difficult tasks the wrong approach can break the integrity of the theory.

Now let's give examples. We all know our planet. You say that it has no magnetic field? You may be right, but scientists say that the processes and interactions inside the Earth's core create a huge magnetic field that stretches for thousands of kilometers. But any magnetic field must have its poles. And they exist, just located a little away from the geographic pole. How do we feel it? For example, birds have developed navigation abilities, and they orient themselves, in particular, by the magnetic field. So, with his help, the geese arrive safely in Lapland. Special navigation devices also use this phenomenon.

Magnetic field sources

The magnetic field is created (generated) by the current of charged particles, or by the time-varying electric field, or by the intrinsic magnetic moments of the particles (the latter, for the sake of uniformity of the picture, can be formally reduced to electric currents).

calculation

In simple cases, the magnetic field of a current-carrying conductor (including the case of a current distributed arbitrarily over volume or space) can be found from the Biot-Savart-Laplace law or the circulation theorem (it is also Ampère's law). In principle, this method is limited to the case (approximation) of magnetostatics - that is, the case of constant (if we are talking about strict applicability) or rather slowly changing (if we are talking about approximate application) magnetic and electric fields.

In more complex situations, it is sought as a solution to Maxwell's equations.

Manifestation of a magnetic field

The magnetic field manifests itself in the effect on the magnetic moments of particles and bodies, on moving charged particles (or current-carrying conductors). The force acting on an electrically charged particle moving in a magnetic field is called the Lorentz force, which is always directed perpendicular to the vectors v and B. It is proportional to the charge of the particle q, the velocity component v, perpendicular to the direction of the magnetic field vector B, and the magnitude of the magnetic field induction B. In the SI system of units, the Lorentz force is expressed as follows:

in the CGS system of units:

where square brackets denote the vector product.

Also (due to the action of the Lorentz force on charged particles moving along the conductor), the magnetic field acts on the conductor with current. The force acting on a current-carrying conductor is called ampere force. This force is the sum of the forces acting on individual charges moving inside the conductor.

Interaction of two magnets

One of the most common in ordinary life manifestations of the magnetic field - the interaction of two magnets: identical poles repel, opposite ones attract. It seems tempting to describe the interaction between magnets as an interaction between two monopoles, and from a formal point of view, this idea is quite realizable and often very convenient, and therefore practically useful (in calculations); however, a detailed analysis shows that in fact this is not completely correct description phenomenon (the most obvious question that cannot be explained within the framework of such a model is the question of why the monopoles can never be separated, that is, why the experiment shows that no isolated body actually has a magnetic charge; in addition, the weakness of the model is that it is inapplicable to a magnetic field created by a macroscopic current, and therefore, if not considered as a purely formal technique, it only leads to a complication of the theory in a fundamental sense).

It would be more correct to say that a magnetic dipole placed in an inhomogeneous field is subject to a force that tends to rotate it so that the magnetic moment of the dipole is co-directed with the magnetic field. But no magnet experiences a (total) force from a uniform magnetic field. Force acting on a magnetic dipole with a magnetic moment m is expressed by the formula:

The force acting on a magnet (which is not a single point dipole) from an inhomogeneous magnetic field can be determined by summing all the forces (defined by this formula) acting on the elementary dipoles that make up the magnet.

However, an approach is possible that reduces the interaction of magnets to the Ampère force, and the formula itself above for the force acting on a magnetic dipole can also be obtained based on the Ampère force.

The phenomenon of electromagnetic induction

vector field H measured in amperes per meter (A/m) in the SI system and in oersteds in the CGS. Oersteds and gausses are identical quantities, their separation is purely terminological.

Magnetic field energy

The increment in the energy density of the magnetic field is:

H- magnetic field strength, B- magnetic induction

In the linear tensor approximation, the magnetic permeability is a tensor (we denote it ) and the multiplication of a vector by it is a tensor (matrix) multiplication:

or in components.

The energy density in this approximation is equal to:

- components of the magnetic permeability tensor , - tensor represented by a matrix inverse to the matrix of the magnetic permeability tensor, - magnetic constant

When the coordinate axes are chosen to coincide with the principal axes of the magnetic permeability tensor, the formulas in the components are simplified:

are the diagonal components of the magnetic permeability tensor in its own axes (the other components in these special coordinates - and only in them! - are equal to zero).

In an isotropic linear magnet:

- relative magnetic permeability

In vacuum and:

The energy of the magnetic field in the inductor can be found by the formula:

Ф - magnetic flux, I - current, L - inductance of a coil or coil with current.

Magnetic properties of substances

From a fundamental point of view, as mentioned above, a magnetic field can be created (and therefore - in the context of this paragraph - and weakened or strengthened) by an alternating electric field, electric currents in the form of streams of charged particles or magnetic moments of particles.

The specific microscopic structure and properties of various substances (as well as their mixtures, alloys, states of aggregation, crystalline modifications, etc.) lead to the fact that at the macroscopic level they can behave quite differently under the action of an external magnetic field (in particular, weakening or amplifying it to varying degrees).

In this regard, substances (and media in general) in relation to their magnetic properties are divided into the following main groups:

Antiferromagnets are substances in which the antiferromagnetic order of the magnetic moments of atoms or ions is established: the magnetic moments of substances are directed oppositely and are equal in strength.
Diamagnets are substances that are magnetized against the direction of an external magnetic field.
Paramagnets are substances that are magnetized in an external magnetic field in the direction of the external magnetic field.
Ferromagnets are substances in which, below a certain critical temperature (Curie point), a long-range ferromagnetic order of magnetic moments is established.
Ferrimagnets - materials in which the magnetic moments of the substance are directed oppositely and are not equal in strength.
The above groups of substances mainly include ordinary solid or (to some) liquid substances, as well as gases. The interaction with the magnetic field of superconductors and plasma differs significantly.

Toki Foucault

Foucault currents (eddy currents) - closed electric currents in a massive conductorarising from a change in the magnetic flux penetrating it. They are induction currents formed in a conducting body either due to a change in time of the magnetic field in which it is located, or as a result of the movement of the body in a magnetic field, leading to a change in the magnetic flux through the body or any part of it. According to Lenz's rule, the magnetic field of Foucault currents is directed so as to oppose the change in magnetic flux that induces these currents.

The history of the development of ideas about the magnetic field

Although magnets and magnetism were known much earlier, the study of the magnetic field began in 1269, when the French scientist Peter Peregrine (the knight Pierre of Méricourt) noted the magnetic field on the surface of a spherical magnet using steel needles and determined that the resulting magnetic field lines intersected at two points, which he called "poles" by analogy with the poles of the Earth. Nearly three centuries later, William Gilbert Colchester used the work of Peter Peregrinus and for the first time definitively stated that the earth itself was a magnet. Published in 1600, Gilbert's work De Magnete, laid the foundations of magnetism as a science.

Three discoveries in a row have challenged this "basis of magnetism." First, in 1819, Hans Christian Oersted discovered that an electric current creates a magnetic field around itself. Then, in 1820, André-Marie Ampère showed that parallel wires carrying current in the same direction attract each other. Finally, Jean-Baptiste Biot and Félix Savard discovered a law in 1820 called the Biot-Savart-Laplace law, which correctly predicted the magnetic field around any live wire.

Expanding on these experiments, Ampère published his own successful model of magnetism in 1825. In it, he showed the equivalence of electric current in magnets, and instead of the dipoles of magnetic charges in the Poisson model, he proposed the idea that magnetism is associated with constantly flowing current loops. This idea explained why the magnetic charge could not be isolated. In addition, Ampère deduced the law named after him, which, like the Biot-Savart-Laplace law, correctly described the magnetic field created by direct current, and the magnetic field circulation theorem was also introduced. Also in this work, Ampère coined the term "electrodynamics" to describe the relationship between electricity and magnetism.

Although the magnetic field strength of a moving electric charge implied in Ampère's law was not explicitly stated, in 1892 Hendrik Lorentz derived it from Maxwell's equations. At the same time, the classical theory of electrodynamics was basically completed.

The twentieth century expanded views on electrodynamics, thanks to the emergence of the theory of relativity and quantum mechanics. Albert Einstein, in his paper in 1905, where his theory of relativity was substantiated, showed that electric and magnetic fields are part of the same phenomenon considered in different systems reference. (See The moving magnet and the conductor problem - the thought experiment that eventually helped Einstein develop special relativity). Finally, quantum mechanics was combined with electrodynamics to form quantum electrodynamics (QED).

Notes

TSB. 1973, "Soviet Encyclopedia".
In special cases, a magnetic field can exist even in the absence of electric field, but generally speaking, the magnetic field is deeply interconnected with the electric field, both dynamically (mutual generation of each other by alternating electric and magnetic fields), and in the sense that upon transition to new system reference, the magnetic and electric fields are expressed through each other, that is, generally speaking, they cannot be unconditionally separated.
Yavorsky B. M., Detlaf A. A. Handbook of Physics: 2nd ed., Revised. - M .: Science, Main edition of physical and mathematical literature, 1985, - 512 p.
In SI, magnetic induction is measured in teslas (T), in the cgs system in gauss.
Exactly coincide in the CGS system of units, in SI they differ by a constant coefficient, which, of course, does not change the fact of their practical physical identity.
The most important and superficial difference here is that the force acting on a moving particle (or on a magnetic dipole) is calculated in terms of and not in terms of . Any other physically correct and meaningful method of measurement will also make it possible to measure it, although sometimes it turns out to be more convenient for a formal calculation - what, in fact, is the point of introducing this auxiliary quantity (otherwise we would do without it at all, using only
However, it must be well understood that a number of fundamental properties of this "matter" are fundamentally different from the properties of that normal look"matter", which could be denoted by the term "substance".
See Ampère's theorem.
For a homogeneous field, this expression gives zero force, since all derivatives are equal to zero B by coordinates.
Sivukhin D.V. General course physics. - Ed. 4th, stereotypical. - M .: Fizmatlit; MIPT Publishing House, 2004. - Vol. III. Electricity. - 656 p. - ISBN 5-9221-0227-3; ISBN 5-89155-086-5.

Magnetic fields occur naturally and can be created artificially. The man noticed them useful features which have learned to apply in Everyday life. What is the source of the magnetic field?

How the doctrine of the magnetic field developed

The magnetic properties of some substances were noticed in antiquity, but their real study began in medieval Europe. Using small steel needles, a scientist from France, Peregrine, discovered the intersection of magnetic lines of force at certain points - the poles. Only three centuries later, guided by this discovery, Gilbert continued to study it and subsequently defended his hypothesis that the Earth has its own magnetic field.

The rapid development of the theory of magnetism began at the beginning of the 19th century, when Ampère discovered and described the influence of an electric field on the occurrence of a magnetic field, and the discovery by Faraday electromagnetic induction established an inverse relationship.

What is a magnetic field

The magnetic field manifests itself in the force effect on electric charges that are in motion, or on bodies that have a magnetic moment.

conductors through which electric current passes;
permanent magnets;
changing electric field.

The root cause of the occurrence of a magnetic field is identical for all sources: electric microcharges - electrons, ions or protons - have their own magnetic moment or are in directed motion.

Important! Mutually generate each other electric and magnetic fields that change over time. This relationship is determined by Maxwell's equations.

Magnetic field characteristics

The characteristics of the magnetic field are:

Magnetic flux, a scalar quantity that determines how many magnetic field lines pass through a given section. Designated with the letter F. Calculated according to the formula:

F = B x S x cos α,

where B is the magnetic induction vector, S is the section, α is the angle of inclination of the vector to the perpendicular drawn to the section plane. Unit of measurement - weber (Wb);

The magnetic induction vector (B) shows the force acting on the charge carriers. It is directed towards the north pole, where the usual magnetic needle points. Quantitatively, magnetic induction is measured in teslas (Tl);
MP tension (N). It is determined by the magnetic permeability of various media. In a vacuum, permeability is taken as unity. The direction of the intensity vector coincides with the direction of the magnetic induction. Unit of measurement - A / m.

How to represent a magnetic field

It is easy to see the manifestations of the magnetic field on the example of a permanent magnet. It has two poles, and depending on the orientation, the two magnets attract or repel. The magnetic field characterizes the processes occurring in this case:

MP is mathematically described as a vector field. It can be constructed by means of many vectors of magnetic induction B, each of which is directed towards the north pole of the compass needle and has a length depending on the magnetic force;
An alternative way of representing is to use lines of force. These lines never intersect, never start or stop anywhere, forming closed loops. The MF lines combine in more frequent regions where the magnetic field is strongest.

Important! The density of field lines indicates the strength of the magnetic field.

Although in reality the MF cannot be seen, the lines of force are easy to visualize in real world, placing iron filings in MP. Each particle behaves like a tiny magnet with a north and south pole. The result is a pattern similar to lines of force. A person is not able to feel the impact of MP.

Magnetic field measurement

Since this is a vector quantity, there are two parameters for measuring MF: force and direction. Direction is easy to measure with a compass connected to the field. An example is a compass placed in the Earth's magnetic field.

Measurement of other characteristics is much more difficult. Practical magnetometers only appeared in the 19th century. Most of them work using the force that the electron feels when moving through the magnetic field.

Very accurate measurement of small magnetic fields has become practical since the discovery in 1988 of giant magnetoresistance in layered materials. This discovery in fundamental physics was quickly applied to magnetic hard disk technology for data storage in computers, resulting in a thousandfold increase in storage capacity in just a few years.

In generally accepted measurement systems, MF is measured in tests (T) or in gauss (Gs). 1 T = 10000 gauss. Gauss is often used because the Tesla is too large a field.

Interesting. A small fridge magnet creates an MF equal to 0.001 T, and the Earth's magnetic field, on average, is 0.00005 T.

The nature of the magnetic field

Magnetism and magnetic fields are manifestations of the electromagnetic force. There are two possible ways how to organize an energy charge in motion and, consequently, a magnetic field.

The first is to connect the wire to a current source, an MF is formed around it.

Important! As the current (the number of charges in motion) increases, the MP increases proportionally. As you move away from the wire, the field decreases with distance. This is described by Ampère's law.

Some materials with higher magnetic permeability are capable of concentrating magnetic fields.

Since the magnetic field is a vector, it is necessary to determine its direction. For an ordinary current flowing through a straight wire, the direction can be found by the right hand rule.

To use the rule, you must imagine that the wire is wrapped right hand, and the thumb indicates the direction of the current. Then the other four fingers will show the direction of the magnetic induction vector around the conductor.

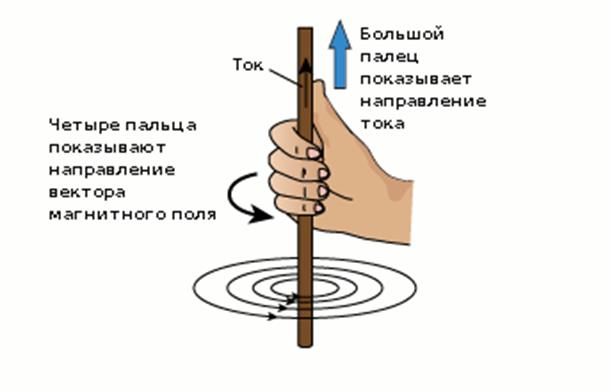
The second way to create an MF is to use the fact that electrons appear in some substances that have their own magnetic moment. This is how permanent magnets work:

Although atoms often have many electrons, they are mostly connected in such a way that the total magnetic field of the pair cancels out. Two electrons paired in this way are said to have opposite spins. Therefore, in order to magnetize something, you need atoms that have one or more electrons with the same spin. For example, iron has four such electrons and is suitable for making magnets;
Billions of electrons in atoms can be randomly oriented, and there will be no common magnetic field, no matter how many unpaired electrons the material has. It must be stable at a low temperature in order to provide an overall preferred electron orientation. The high magnetic permeability causes the magnetization of such substances under certain conditions outside the influence of the magnetic field. These are ferromagnets;
Other materials may exhibit magnetic properties in the presence of an external magnetic field. The external field serves to equalize all electron spins, which disappears after the removal of the MF. These substances are paramagnetic. Refrigerator door metal is an example of a paramagnet.

The earth can be represented in the form of capacitor plates, the charge of which has opposite sign: "minus" - at earth's surface and "plus" - in the ionosphere. Between them is atmospheric air as an insulating pad. The giant capacitor retains a constant charge due to the influence of the earth's magnetic field. Using this knowledge, it is possible to create a scheme for obtaining electrical energy from the Earth's magnetic field. True, the result will be low voltage values.

Have to take:

grounding device;
the wire;
Tesla transformer, capable of generating high-frequency oscillations and creating a corona discharge, ionizing the air.

The Tesla coil will act as an electron emitter. The whole structure is connected together, and in order to ensure a sufficient potential difference, the transformer must be raised to a considerable height. Thus, it will be created electrical circuit through which a small current will flow. Get a large number of electricity using this device is not possible.

Electricity and magnetism dominate many of the worlds surrounding man: from the most fundamental processes in nature to cutting-edge electronic devices.

Video

Just as an electric charge at rest acts on another charge through an electric field, an electric current acts on another current through magnetic field. The action of a magnetic field on permanent magnets is reduced to its action on charges moving in the atoms of a substance and creating microscopic circular currents.

Doctrine of electromagnetism based on two assumptions:

the magnetic field acts on moving charges and currents;
a magnetic field arises around currents and moving charges.

Interaction of magnets

Permanent magnet(or magnetic needle) is oriented along the magnetic meridian of the Earth. The end pointing north is called north pole(N) and the opposite end is south pole(S). Approaching two magnets to each other, we note that their like poles repel, and opposite ones attract ( rice. one ).

If we separate the poles by cutting the permanent magnet into two parts, then we will find that each of them will also have two poles, i.e. will be a permanent magnet ( rice. 2 ). Both poles - north and south - are inseparable from each other, equal.

The magnetic field created by the Earth or permanent magnets is depicted, like the electric field, by magnetic lines of force. A picture of the magnetic field lines of any magnet can be obtained by placing a sheet of paper over it, on which iron filings are poured in a uniform layer. Getting into a magnetic field, the sawdust is magnetized - each of them has a north and south poles. Opposite poles tend to approach each other, but this is prevented by the friction of sawdust on paper. If you tap the paper with your finger, the friction will decrease and the filings will be attracted to each other, forming chains that represent the lines of a magnetic field.

On the rice. 3 shows the location in the field of a direct magnet of sawdust and small magnetic arrows indicating the direction of the magnetic field lines. For this direction, the direction of the north pole of the magnetic needle is taken.

Oersted's experience. Magnetic field current

AT early XIX in. Danish scientist Oersted did important discovery, discovering action of electric current on permanent magnets . He placed a long wire near the magnetic needle. When a current was passed through the wire, the arrow turned, trying to be perpendicular to it ( rice. four ). This could be explained by the appearance of a magnetic field around the conductor.

The magnetic lines of force of the field created by a direct conductor with current are concentric circles located in a plane perpendicular to it, with centers at the point through which the current passes ( rice. 5 ). The direction of the lines is determined by the right screw rule:

If the screw is rotated in the direction of the field lines, it will move in the direction of the current in the conductor .

The force characteristic of the magnetic field is magnetic induction vector B . At each point, it is directed tangentially to the field line. Electric field lines start at positive charges and end in negative, and the force acting in this field on the charge is directed tangentially to the line at each of its points. Unlike the electric field, the lines of the magnetic field are closed, which is due to the absence of "magnetic charges" in nature.

The magnetic field of the current is fundamentally no different from the field created by a permanent magnet. In this sense, an analogue of a flat magnet is a long solenoid - a coil of wire, the length of which is much greater than its diameter. The diagram of the lines of the magnetic field he created, depicted in rice. 6 , similar to that for a flat magnet ( rice. 3 ). The circles indicate the sections of the wire forming the solenoid winding. The currents flowing through the wire from the observer are indicated by crosses, and the currents in the opposite direction - towards the observer - are indicated by dots. The same designations are accepted for magnetic field lines when they are perpendicular to the plane of the drawing ( rice. 7 a, b).

The direction of the current in the solenoid winding and the direction of the magnetic field lines inside it are also related by the right screw rule, which in this case is formulated as follows:

If you look along the axis of the solenoid, then the current flowing in the clockwise direction creates a magnetic field in it, the direction of which coincides with the direction of movement of the right screw ( rice. eight )

Based on this rule, it is easy to figure out that the solenoid shown in rice. 6 , its right end is the north pole, and its left end is the south pole.

The magnetic field inside the solenoid is homogeneous - the magnetic induction vector has a constant value there (B = const). In this respect, the solenoid is similar to a flat capacitor, inside which a uniform electric field is created.

The force acting in a magnetic field on a conductor with current

It was experimentally established that a force acts on a current-carrying conductor in a magnetic field. In a uniform field, a rectilinear conductor of length l, through which current I flows, located perpendicular to the field vector B, experiences the force: F = I l B .

The direction of the force is determined left hand rule:

If the four outstretched fingers of the left hand are placed in the direction of the current in the conductor, and the palm is perpendicular to the vector B, then the retracted thumb will indicate the direction of the force acting on the conductor (rice. 9 ).

It should be noted that the force acting on a conductor with current in a magnetic field is not directed tangentially to its lines of force, like an electric force, but perpendicular to them. A conductor located along the lines of force is not affected by the magnetic force.

The equation F = IlB allows to give a quantitative characteristic of the magnetic field induction.

Attitude does not depend on the properties of the conductor and characterizes the magnetic field itself.

The module of the magnetic induction vector B is numerically equal to the force acting on a conductor of unit length located perpendicular to it, through which a current of one ampere flows.

In the SI system, the unit of magnetic field induction is tesla (T):

A magnetic field. Tables, diagrams, formulas

(Interaction of magnets, Oersted's experiment, magnetic induction vector, vector direction, superposition principle. Graphic image magnetic fields, lines of magnetic induction. Magnetic flux, energy characteristic of the field. Magnetic forces, Ampere force, Lorentz force. Movement of charged particles in a magnetic field. Magnetic properties of matter, Ampere's hypothesis)