Properties of roots, formulations, proofs, examples. Square root. Detailed theory with examples Square root, arithmetic square root

\(\sqrt(a)=b\) if \(b^2=a\), where \(a≥0,b≥0\)

Examples:

\(\sqrt(49)=7\) because \(7^2=49\)
\(\sqrt(0.04)=0.2\),because \(0.2^2=0.04\)

How to extract the square root of a number?

To extract the square root of a number, you need to ask yourself the question: what number squared will give the expression under the root?

for example. Extract the root: a)\(\sqrt(2500)\); b) \(\sqrt(\frac(4)(9))\); c) \(\sqrt(0.001)\); d) \(\sqrt(1\frac(13)(36))\)

a) What number squared will give \(2500\)?

\(\sqrt(2500)=50\)

b) What number squared will give \(\frac(4)(9)\) ?

\(\sqrt(\frac(4)(9))\) \(=\)\(\frac(2)(3)\)

c) What number squared will give \(0.0001\)?

\(\sqrt(0.0001)=0.01\)

d) What squared number will \(\sqrt(1\frac(13)(36))\) give? To give an answer to the question, you need to translate into the wrong one.

\(\sqrt(1\frac(13)(36))=\sqrt(\frac(49)(16))=\frac(7)(6)\)

Comment: Although \(-50\), \(-\frac(2)(3)\) , \(-0,01\),\(- \frac(7)(6)\) also answer the given questions, but they are not taken into account, since the square root is always positive.

The main property of the root

As you know, in mathematics, any action has an inverse. Addition has subtraction, multiplication has division. The opposite of squaring is taking the square root. Therefore, these actions cancel each other out:

\((\sqrt(a))^2=a\)

This is the main property of the root, which is most often used (including in the OGE)

Example . (task from the OGE). Find the value of the expression \(\frac((2\sqrt(6))^2)(36)\)

Decision :\(\frac((2\sqrt(6))^2)(36)=\frac(4 \cdot (\sqrt(6))^2)(36)=\frac(4 \cdot 6)(36 )=\frac(4)(6)=\frac(2)(3)\)

Example . (task from the OGE). Find the value of the expression \((\sqrt(85)-1)^2\)

Decision:

Of course, when working with a square root, you need to use others.

Example . (task from the OGE). Find the value of the expression \(5\sqrt(11) \cdot 2\sqrt(2)\cdot \sqrt(22)\)
Decision:

Answer: \(220\)

4 rules that are always forgotten

The root is not always extracted

Example: \(\sqrt(2)\),\(\sqrt(53)\),\(\sqrt(200)\),\(\sqrt(0,1)\) etc. - extracting a root from a number is not always possible and this is normal!

Root of a number, also a number

No need to treat \(\sqrt(2)\), \(\sqrt(53)\) in any special way. These are numbers, but not integers, yes, but not everything in our world is measured in integers.

The root is taken only from non-negative numbers

Therefore, in textbooks you will not see such entries \(\sqrt(-23)\),\(\sqrt(-1)\), etc.

I looked again at the plate ... And, let's go!

Let's start with a simple one:

Wait a minute. this, which means we can write it like this:

Got it? Here's the next one for you:

The roots of the resulting numbers are not exactly extracted? Don't worry, here are some examples:

But what if there are not two multipliers, but more? The same! The root multiplication formula works with any number of factors:

Now completely independent:

Answers: Well done! Agree, everything is very easy, the main thing is to know the multiplication table!

Root division

We figured out the multiplication of the roots, now let's proceed to the property of division.

Let me remind you that the formula in general looks like this:

And that means that the root of the quotient is equal to the quotient of the roots.

Well, let's look at examples:

That's all science. And here's an example:

Everything is not as smooth as in the first example, but as you can see, there is nothing complicated.

What if the expression looks like this:

You just need to apply the formula in reverse:

And here's an example:

You can also see this expression:

Everything is the same, only here you need to remember how to translate fractions (if you don’t remember, look at the topic and come back!). Remembered? Now we decide!

I am sure that you coped with everything, everything, now let's try to build roots in a degree.

Exponentiation

What happens if the square root is squared? It's simple, remember the meaning of the square root of a number - this is a number whose square root is equal to.

So, if we square a number whose square root is equal, then what do we get?

Well, of course, !

Let's look at examples:

Everything is simple, right? And if the root is in a different degree? It's OK!

Stick to the same logic and remember the properties and possible actions with degrees.

Read the theory on the topic "" and everything will become extremely clear to you.

For example, here's an expression:

In this example, the degree is even, but what if it is odd? Again, apply the power properties and factor everything:

With this, everything seems to be clear, but how to extract the root from a number in a degree? Here, for example, is this:

Pretty simple, right? What if the degree is greater than two? We follow the same logic using the properties of degrees:

Well, is everything clear? Then solve your own examples:

And here are the answers:

Introduction under the sign of the root

What we just have not learned to do with the roots! It remains only to practice entering the number under the root sign!

It's quite easy!

Let's say we have a number

What can we do with it? Well, of course, hide the triple under the root, while remembering that the triple is the square root of!

Why do we need it? Yes, just to expand our capabilities when solving examples:

How do you like this property of roots? Makes life much easier? For me, that's right! Only we must remember that we can only enter positive numbers under the square root sign.

Try this example for yourself:
Did you manage? Let's see what you should get:

Well done! You managed to enter a number under the root sign! Let's move on to the equally important - consider how to compare numbers containing a square root!

Root Comparison

Why should we learn to compare numbers containing a square root?

Very simple. Often, in large and long expressions encountered in the exam, we get an irrational answer (remember what it is? We already talked about this today!)

We need to place the received answers on the coordinate line, for example, to determine which interval is suitable for solving the equation. And this is where the snag arises: there is no calculator on the exam, and without it, how to imagine which number is larger and which is smaller? That's it!

For example, determine which is greater: or?

You won't say right off the bat. Well, let's use the parsed property of adding a number under the root sign?

Then forward:

Well, obviously, the larger the number under the sign of the root, the larger the root itself!

Those. if means .

From this we firmly conclude that And no one will convince us otherwise!

Extracting roots from large numbers

Before that, we introduced a factor under the sign of the root, but how to take it out? You just need to factor it out and extract what is extracted!

It was possible to go the other way and decompose into other factors:

Not bad, right? Any of these approaches is correct, decide how you feel comfortable.

Factoring is very useful when solving such non-standard tasks as this one:

We don't get scared, we act! We decompose each factor under the root into separate factors:

And now try it yourself (without a calculator! It will not be on the exam):

Is this the end? We don't stop halfway!

That's all, it's not all that scary, right?

Happened? Well done, you're right!

Now try this example:

And an example is a tough nut to crack, so you can’t immediately figure out how to approach it. But we, of course, are in the teeth.

Well, let's start factoring, shall we? Immediately, we note that you can divide a number by (recall the signs of divisibility):

And now, try it yourself (again, without a calculator!):

Well, did it work? Well done, you're right!

Summing up

1. The square root (arithmetic square root) of a non-negative number is a non-negative number whose square is equal.
   .
2. If we just take the square root of something, we always get one non-negative result.
3. Arithmetic root properties:
4. When comparing square roots, it must be remembered that the larger the number under the sign of the root, the larger the root itself.

How do you like the square root? All clear?

We tried to explain to you without water everything you need to know in the exam about the square root.

It's your turn. Write to us whether this topic is difficult for you or not.

Did you learn something new or everything was already so clear.

Write in the comments and good luck on the exams!

Congratulations: today we will analyze the roots - one of the most mind-blowing topics of the 8th grade. :)

Many people get confused about the roots, not because they are complex (which is complicated - a couple of definitions and a couple more properties), but because in most school textbooks the roots are defined through such wilds that only the authors of the textbooks themselves can understand this scribbling. And even then only with a bottle of good whiskey. :)

Therefore, now I will give the most correct and most competent definition of the root - the only one that you really need to remember. And only then I will explain: why all this is necessary and how to apply it in practice.

But first, remember one important point, which for some reason many compilers of textbooks “forget” about:

Roots can be of even degree (our favorite $\sqrt(a)$, as well as any $\sqrt(a)$ and even $\sqrt(a)$) and odd degree (any $\sqrt(a)$, $\ sqrt(a)$ etc.). And the definition of the root of an odd degree is somewhat different from the even one.

Here in this fucking “somewhat different” is hidden, probably, 95% of all errors and misunderstandings associated with the roots. So let's clear up the terminology once and for all:

Definition. Even root n from the number $a$ is any non-negative a number $b$ such that $((b)^(n))=a$. And the root of an odd degree from the same number $a$ is generally any number $b$ for which the same equality holds: $((b)^(n))=a$.

In any case, the root is denoted like this:

\(a)\]

The number $n$ in such a notation is called the root exponent, and the number $a$ is called the radical expression. In particular, for $n=2$ we get our “favorite” square root (by the way, this is a root of an even degree), and for $n=3$ we get a cubic root (an odd degree), which is also often found in problems and equations.

Examples. Classic examples of square roots:

\[\begin(align) & \sqrt(4)=2; \\ & \sqrt(81)=9; \\ & \sqrt(256)=16. \\ \end(align)\]

By the way, $\sqrt(0)=0$ and $\sqrt(1)=1$. This is quite logical since $((0)^(2))=0$ and $((1)^(2))=1$.

Cubic roots are also common - do not be afraid of them:

\[\begin(align) & \sqrt(27)=3; \\ & \sqrt(-64)=-4; \\ & \sqrt(343)=7. \\ \end(align)\]

Well, a couple of "exotic examples":

\[\begin(align) & \sqrt(81)=3; \\ & \sqrt(-32)=-2. \\ \end(align)\]

If you do not understand what is the difference between an even and an odd degree, reread the definition again. It is very important!

In the meantime, we will consider one unpleasant feature of the roots, because of which we needed to introduce a separate definition for even and odd exponents.

Why do we need roots at all?

After reading the definition, many students will ask: “What did mathematicians smoke when they came up with this?” And really: why do we need all these roots?

To answer this question, let's go back to elementary school for a moment. Remember: in those distant times, when the trees were greener and the dumplings were tastier, our main concern was to multiply the numbers correctly. Well, something in the spirit of "five by five - twenty-five", that's all. But after all, you can multiply numbers not in pairs, but in triplets, fours, and generally whole sets:

\[\begin(align) & 5\cdot 5=25; \\ & 5\cdot 5\cdot 5=125; \\ & 5\cdot 5\cdot 5\cdot 5=625; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5=3125; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5=15\ 625. \end(align)\]

However, this is not the point. The trick is different: mathematicians are lazy people, so they had to write down the multiplication of ten fives like this:

So they came up with degrees. Why not write the number of factors as a superscript instead of a long string? Like this one:

It's very convenient! All calculations are reduced by several times, and you can not spend a bunch of parchment sheets of notebooks to write down some 5 183 . Such an entry was called the degree of a number, a bunch of properties were found in it, but happiness turned out to be short-lived.

After a grandiose booze, which was organized just about the “discovery” of degrees, some especially stoned mathematician suddenly asked: “What if we know the degree of a number, but we don’t know the number itself?” Indeed, if we know that a certain number $b$, for example, gives 243 to the 5th power, then how can we guess what the number $b$ itself is equal to?

This problem turned out to be much more global than it might seem at first glance. Because it turned out that for the majority of “ready-made” degrees there are no such “initial” numbers. Judge for yourself:

\[\begin(align) & ((b)^(3))=27\Rightarrow b=3\cdot 3\cdot 3\Rightarrow b=3; \\ & ((b)^(3))=64\Rightarrow b=4\cdot 4\cdot 4\Rightarrow b=4. \\ \end(align)\]

What if $((b)^(3))=50$? It turns out that you need to find a certain number, which, when multiplied by itself three times, will give us 50. But what is this number? It is clearly greater than 3 because 3 3 = 27< 50. С тем же успехом оно меньше 4, поскольку 4 3 = 64 >50. I.e. this number lies somewhere between three and four, but what it is equal to - FIG you will understand.

This is exactly why mathematicians came up with $n$-th roots. That is why the radical icon $\sqrt(*)$ was introduced. To denote the same number $b$, which, to the specified power, will give us a previously known value

\[\sqrt[n](a)=b\Rightarrow ((b)^(n))=a\]

I do not argue: often these roots are easily considered - we saw several such examples above. But still, in most cases, if you think of an arbitrary number, and then try to extract the root of an arbitrary degree from it, you are in for a cruel bummer.

What is there! Even the simplest and most familiar $\sqrt(2)$ cannot be represented in our usual form - as an integer or a fraction. And if you drive this number into a calculator, you will see this:

\[\sqrt(2)=1.414213562...\]

As you can see, after the decimal point there is an endless sequence of numbers that do not obey any logic. You can, of course, round this number to quickly compare with other numbers. For example:

\[\sqrt(2)=1.4142...\approx 1.4 \lt 1.5\]

Or here's another example:

\[\sqrt(3)=1.73205...\approx 1.7 \gt 1.5\]

But all these roundings are, firstly, rather rough; and secondly, you also need to be able to work with approximate values, otherwise you can catch a bunch of non-obvious errors (by the way, the skill of comparison and rounding is necessarily checked at the profile exam).

Therefore, in serious mathematics, one cannot do without roots - they are the same equal representatives of the set of all real numbers $\mathbb(R)$, like fractions and integers that we have long known.

The impossibility of representing the root as a fraction of the form $\frac(p)(q)$ means that this root is not a rational number. Such numbers are called irrational, and they cannot be accurately represented except with the help of a radical, or other constructions specially designed for this (logarithms, degrees, limits, etc.). But more on that another time.

Consider a few examples where, after all the calculations, irrational numbers will still remain in the answer.

\[\begin(align) & \sqrt(2+\sqrt(27))=\sqrt(2+3)=\sqrt(5)\approx 2,236... \\ & \sqrt(\sqrt(-32 ))=\sqrt(-2)\approx -1,2599... \\ \end(align)\]

Naturally, by the appearance of the root, it is almost impossible to guess which numbers will come after the decimal point. However, it is possible to calculate on a calculator, but even the most advanced date calculator gives us only the first few digits of an irrational number. Therefore, it is much more correct to write the answers as $\sqrt(5)$ and $\sqrt(-2)$.

That's what they were invented for. To make it easy to write down answers.

Why are two definitions needed?

The attentive reader has probably already noticed that all the square roots given in the examples are taken from positive numbers. Well, at least from zero. But cube roots are calmly extracted from absolutely any number - even positive, even negative.

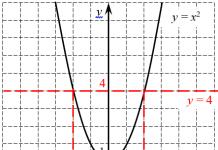
Why is this happening? Take a look at the graph of the function $y=((x)^(2))$:

Let's try to calculate $\sqrt(4)$ using this graph. To do this, a horizontal line $y=4$ (marked in red) is drawn on the graph, which intersects the parabola at two points: $((x)_(1))=2$ and $((x)_(2)) =-2$. This is quite logical, since

Everything is clear with the first number - it is positive, therefore it is the root:

But then what to do with the second point? Does the 4 have two roots at once? After all, if we square the number −2, we also get 4. Why not write $\sqrt(4)=-2$ then? And why do teachers look at such records as if they want to eat you? :)

The trouble is that if no additional conditions are imposed, then the four will have two square roots - positive and negative. And any positive number will also have two of them. But negative numbers will not have roots at all - this can be seen from the same graph, since the parabola never falls below the axis y, i.e. does not take negative values.

A similar problem occurs for all roots with an even exponent:

1. Strictly speaking, each positive number will have two roots with an even exponent $n$;
2. From negative numbers, the root with even $n$ is not extracted at all.

That is why the definition of an even root $n$ specifically stipulates that the answer must be a non-negative number. This is how we get rid of ambiguity.

But for odd $n$ there is no such problem. To see this, let's take a look at the graph of the function $y=((x)^(3))$:

Two conclusions can be drawn from this graph:

1. The branches of a cubic parabola, unlike the usual one, go to infinity in both directions - both up and down. Therefore, at whatever height we draw a horizontal line, this line will definitely intersect with our graph. Therefore, the cube root can always be taken, absolutely from any number;
2. In addition, such an intersection will always be unique, so you don’t need to think about which number to consider the “correct” root, and which one to score. That is why the definition of roots for an odd degree is simpler than for an even one (there is no non-negativity requirement).

It's a pity that these simple things are not explained in most textbooks. Instead, our brains begin to soar with all sorts of arithmetic roots and their properties.

Yes, I do not argue: what is an arithmetic root - you also need to know. And I will talk about this in detail in a separate lesson. Today we will also talk about it, because without it, all reflections on the roots of the $n$-th multiplicity would be incomplete.

But first you need to clearly understand the definition that I gave above. Otherwise, due to the abundance of terms, such a mess will begin in your head that in the end you will not understand anything at all.

And all you need to understand is the difference between even and odd numbers. Therefore, once again we will collect everything that you really need to know about the roots:

1. An even root exists only from a non-negative number and is itself always a non-negative number. For negative numbers, such a root is undefined.
2. But the root of an odd degree exists from any number and can itself be any number: for positive numbers it is positive, and for negative numbers, as the cap hints, it is negative.

Is it difficult? No, it's not difficult. Understandably? Yes, it's obvious! Therefore, now we will practice a little with the calculations.

Basic properties and restrictions

Roots have a lot of strange properties and restrictions - this will be a separate lesson. Therefore, now we will consider only the most important "chip", which applies only to roots with an even exponent. We write this property in the form of a formula:

\[\sqrt(((x)^(2n)))=\left| x\right|\]

In other words, if we raise a number to an even power, and then extract the root of the same degree from this, we will get not the original number, but its modulus. This is a simple theorem that is easy to prove (it suffices to consider separately non-negative $x$, and then separately consider negative ones). Teachers constantly talk about it, it is given in every school textbook. But as soon as it comes to solving irrational equations (i.e. equations containing the sign of the radical), the students forget this formula together.

To understand the issue in detail, let's forget all the formulas for a minute and try to count two numbers ahead:

\[\sqrt(((3)^(4)))=?\quad \sqrt(((\left(-3 \right))^(4)))=?\]

These are very simple examples. The first example will be solved by most of the people, but on the second, many stick. To solve any such crap without problems, always consider the procedure:

1. First, the number is raised to the fourth power. Well, it's kind of easy. A new number will be obtained, which can even be found in the multiplication table;
2. And now from this new number it is necessary to extract the root of the fourth degree. Those. there is no "reduction" of roots and degrees - these are sequential actions.

Let's deal with the first expression: $\sqrt(((3)^(4)))$. Obviously, you first need to calculate the expression under the root:

\[((3)^(4))=3\cdot 3\cdot 3\cdot 3=81\]

Then we extract the fourth root of the number 81:

Now let's do the same with the second expression. First, we raise the number −3 to the fourth power, for which we need to multiply it by itself 4 times:

\[((\left(-3 \right))^(4))=\left(-3 \right)\cdot \left(-3 \right)\cdot \left(-3 \right)\cdot \ left(-3 \right)=81\]

We got a positive number, since the total number of minuses in the product is 4 pieces, and they will all cancel each other out (after all, a minus by a minus gives a plus). Next, extract the root again:

In principle, this line could not be written, since it is a no brainer that the answer will be the same. Those. an even root of the same even power "burns" the minuses, and in this sense the result is indistinguishable from the usual module:

\[\begin(align) & \sqrt(((3)^(4)))=\left| 3\right|=3; \\ & \sqrt(((\left(-3 \right))^(4)))=\left| -3 \right|=3. \\ \end(align)\]

These calculations are in good agreement with the definition of the root of an even degree: the result is always non-negative, and the radical sign is also always a non-negative number. Otherwise, the root is not defined.

Note on the order of operations

1. The notation $\sqrt(((a)^(2)))$ means that we first square the number $a$, and then take the square root of the resulting value. Therefore, we can be sure that a non-negative number always sits under the root sign, since $((a)^(2))\ge 0$ anyway;
2. But the notation $((\left(\sqrt(a) \right))^(2))$, on the contrary, means that we first extract the root from a certain number $a$ and only then square the result. Therefore, the number $a$ in no case can be negative - this is a mandatory requirement embedded in the definition.

Thus, in no case should one thoughtlessly reduce the roots and degrees, thereby supposedly "simplifying" the original expression. Because if there is a negative number under the root, and its exponent is even, we will get a lot of problems.

However, all these problems are relevant only for even indicators.

Removing a minus sign from under the root sign

Naturally, roots with odd exponents also have their own feature, which, in principle, does not exist for even ones. Namely:

\[\sqrt(-a)=-\sqrt(a)\]

In short, you can take out a minus from under the sign of the roots of an odd degree. This is a very useful property that allows you to "throw" all the minuses out:

\[\begin(align) & \sqrt(-8)=-\sqrt(8)=-2; \\ & \sqrt(-27)\cdot \sqrt(-32)=-\sqrt(27)\cdot \left(-\sqrt(32) \right)= \\ & =\sqrt(27)\cdot \sqrt(32)= \\ & =3\cdot 2=6. \end(align)\]

This simple property greatly simplifies many calculations. Now you don’t need to worry: what if a negative expression got under the root, and the degree at the root turned out to be even? It is enough just to “throw out” all the minuses outside the roots, after which they can be multiplied by each other, divided and generally do many suspicious things, which in the case of “classic” roots are guaranteed to lead us to an error.

And here another definition enters the scene - the very one with which most schools begin the study of irrational expressions. And without which our reasoning would be incomplete. Meet!

arithmetic root

Let's assume for a moment that only positive numbers or, in extreme cases, zero can be under the root sign. Let's score on even / odd indicators, score on all the definitions given above - we will work only with non-negative numbers. What then?

And then we get the arithmetic root - it partially intersects with our "standard" definitions, but still differs from them.

Definition. An arithmetic root of the $n$th degree of a non-negative number $a$ is a non-negative number $b$ such that $((b)^(n))=a$.

As you can see, we are no longer interested in parity. Instead, a new restriction appeared: the radical expression is now always non-negative, and the root itself is also non-negative.

To better understand how the arithmetic root differs from the usual one, take a look at the graphs of the square and cubic parabola already familiar to us:

As you can see, from now on, we are only interested in those pieces of graphs that are located in the first coordinate quarter - where the coordinates $x$ and $y$ are positive (or at least zero). You no longer need to look at the indicator to understand whether we have the right to root a negative number or not. Because negative numbers are no longer considered in principle.

You may ask: “Well, why do we need such a castrated definition?” Or: "Why can't we get by with the standard definition given above?"

Well, I will give just one property, because of which the new definition becomes appropriate. For example, the exponentiation rule:

\[\sqrt[n](a)=\sqrt(((a)^(k)))\]

Please note: we can raise the radical expression to any power and at the same time multiply the root exponent by the same power - and the result will be the same number! Here are some examples:

\[\begin(align) & \sqrt(5)=\sqrt(((5)^(2)))=\sqrt(25) \\ & \sqrt(2)=\sqrt(((2)^ (4)))=\sqrt(16) \\ \end(align)\]

Well, what's wrong with that? Why couldn't we do it before? Here's why. Consider a simple expression: $\sqrt(-2)$ is a number that is quite normal in our classical sense, but absolutely unacceptable from the point of view of the arithmetic root. Let's try to convert it:

$\begin(align) & \sqrt(-2)=-\sqrt(2)=-\sqrt(((2)^(2)))=-\sqrt(4) \lt 0; \\ & \sqrt(-2)=\sqrt(((\left(-2 \right))^(2)))=\sqrt(4) \gt 0. \\ \end(align)$

As you can see, in the first case, we took the minus out from under the radical (we have every right, because the indicator is odd), and in the second, we used the above formula. Those. from the point of view of mathematics, everything is done according to the rules.

WTF?! How can the same number be both positive and negative? No way. It's just that the exponentiation formula, which works great for positive numbers and zero, starts to give complete heresy in the case of negative numbers.

Here, in order to get rid of such ambiguity, they came up with arithmetic roots. A separate large lesson is devoted to them, where we consider in detail all their properties. So now we will not dwell on them - the lesson turned out to be too long anyway.

Algebraic root: for those who want to know more

I thought for a long time: to make this topic in a separate paragraph or not. In the end, I decided to leave here. This material is intended for those who want to understand the roots even better - no longer at the average “school” level, but at the level close to the Olympiad.

So: in addition to the "classical" definition of the root of the $n$-th degree from a number and the associated division into even and odd indicators, there is a more "adult" definition, which does not depend on parity and other subtleties at all. This is called an algebraic root.

Definition. An algebraic $n$-th root of any $a$ is the set of all numbers $b$ such that $((b)^(n))=a$. There is no well-established designation for such roots, so just put a dash on top:

\[\overline(\sqrt[n](a))=\left\( b\left| b\in \mathbb(R);((b)^(n))=a \right. \right\) \]

The fundamental difference from the standard definition given at the beginning of the lesson is that the algebraic root is not a specific number, but a set. And since we are working with real numbers, this set is of only three types:

1. Empty set. Occurs when it is required to find an algebraic root of an even degree from a negative number;
2. A set consisting of a single element. All roots of odd powers, as well as roots of even powers from zero, fall into this category;
3. Finally, the set can include two numbers - the same $((x)_(1))$ and $((x)_(2))=-((x)_(1))$ that we saw on the chart quadratic function. Accordingly, such an alignment is possible only when extracting the root of an even degree from a positive number.

The last case deserves more detailed consideration. Let's count a couple of examples to understand the difference.

Example. Compute expressions:

\[\overline(\sqrt(4));\quad \overline(\sqrt(-27));\quad \overline(\sqrt(-16)).\]

Decision. The first expression is simple:

\[\overline(\sqrt(4))=\left\( 2;-2 \right\)\]

It is two numbers that are part of the set. Because each of them squared gives a four.

\[\overline(\sqrt(-27))=\left\( -3 \right\)\]

Here we see a set consisting of only one number. This is quite logical, since the exponent of the root is odd.

Finally, the last expression:

\[\overline(\sqrt(-16))=\varnothing \]

We got an empty set. Because there is not a single real number that, when raised to the fourth (that is, even!) Power, will give us a negative number −16.

Final note. Please note: it was not by chance that I noted everywhere that we are working with real numbers. Because there are also complex numbers - it is quite possible to calculate $\sqrt(-16)$ and many other strange things there.

However, in the modern school curriculum of mathematics, complex numbers are almost never found. They have been omitted from most textbooks because our officials consider the topic "too difficult to understand."

That's all. In the next lesson, we will look at all the key properties of roots and finally learn how to simplify irrational expressions. :)

Root formulas. properties of square roots.

Attention!
There are additional
material in Special Section 555.
For those who strongly "not very..."
And for those who "very much...")

In the previous lesson, we figured out what a square root is. It's time to figure out what are formulas for roots, what are root properties and what can be done about it all.

Root Formulas, Root Properties, and Rules for Actions with Roots- it's essentially the same thing. There are surprisingly few formulas for square roots. Which, of course, pleases! Rather, you can write a lot of all sorts of formulas, but only three are enough for practical and confident work with roots. Everything else flows from these three. Although many stray in the three formulas of the roots, yes ...

Let's start with the simplest. Here she is:

If you like this site...

By the way, I have a couple more interesting sites for you.)

You can practice solving examples and find out your level. Testing with instant verification. Learning - with interest!)

you can get acquainted with functions and derivatives.

Husband. root, necks, root · detract. contemptuous rhizome, magnifying rhizome, underground part of every plant. In trees, the backbone and lateral roots are distinguished, and with them there are roots and small lobes. absorbing moisture. The root happens: bulbous, ... ... Dahl's Explanatory Dictionary

ROOT, pH, pl. rni, rni, husband. 1. The underground part of the plant, which serves to strengthen it in the soil and absorb water and nutrients from it. Main, lateral, adnexal to. Aerial roots (in lianas and some other plants high above the ground ... Explanatory dictionary of Ozhegov

- (radix), one of the main vegetative organs of leafy plants, which serves to attach to the substrate, absorb water from it and nourish. substances. Phylogenetically, K. arose later than the stem, and probably descended from root-like ... ... Biological encyclopedic dictionary

See beginning, reason, origin uproot, take root... Dictionary of Russian synonyms and expressions similar in meaning. under. ed. N. Abramova, M .: Russian dictionaries, 1999. root, beginning, reason, origin; radical; spine, stem, ... ... Synonym dictionary

root- ROOT, rnya, m. 1. Friend, buddy. 2. Male sexual organ A small man grows into a root root A strong root is an old, faithful friend. 1. possible contamination with sidekick… Dictionary of Russian Argo

In mathematics ..1) the root of degree n from the number a is any number x (denoted, a is called a radical expression), the nth degree of which is equal to a (). The action of finding the root is called extracting the root2)] The root of the equation is the number that after ... ...

The primary root is preserved in many conifers for life and develops in the form of a powerful tap root, from which the lateral ones extend. Less commonly, as in some pines, the primary root is underdeveloped and replaced by lateral ones. Apart from the long... Biological Encyclopedia

- (mathematical), 1) The root of the degree n of the number a A number whose nth power is equal to the given number a (denoted; a is called a radical expression). The act of finding a root is called extracting the root. 2) Solution of the equation value ... ... Modern Encyclopedia

In biology, one of the main organs of plants, which serves to strengthen in the soil, absorb water, minerals, synthesize organic compounds, and also to isolate some metabolic products. The root can be a storage place for spare ... ... Big Encyclopedic Dictionary

In linguistics, a non-derivative (simple) word stem that does not include any affixes. The root is the lexical core of the word, that is, it carries its main real meaning ... Big Encyclopedic Dictionary

Books

• The Root of All Evil, Williams R. Donald Bailey is not a difficult teenager, but simply unhappy. Having committed an irreparable act, he lost the trust of friends, the love of his mother and his own peace. What is left for him? Run away from...
• The Root of the Problem, Henry R. Brandt. The author of this book offers a very simple Biblical truth of deliverance from all kinds of mental disorders: awareness of sin as the root cause of all problems and repentance for sins committed. AT…