TEKST OBJAŠNJENJE LEKCIJE:
Ideja o ravnini u prostoru omogućuje vam da dobijete, na primjer, površinu stola ili zida. Međutim, stol ili zid imaju konačne dimenzije, a ravnina se proteže izvan njihovih granica u beskonačnost.
Razmotrimo dvije ravnine koje se sijeku. Kada se sijeku, tvore četiri diedralna kuta sa zajedničkim rubom.
Prisjetimo se što je diedralni kut.
U stvarnosti se susrećemo s objektima koji imaju oblik diedralnog kuta: na primjer, odškrinuta vrata ili poluotvorena mapa.
Na presjeku dviju ravnina alfa i beta dobivamo četiri diedralna kuta. Neka je jedan od diedralnih kutova jednak (phi), tada je drugi jednak (1800 -), treći, četvrti (1800-).
Razmotrimo slučaj kada je jedan od diedarskih kutova jednak 900.
Tada su svi diedralni kutovi u ovom slučaju jednaki 900.
Uvedemo definiciju okomitih ravnina:
Za dvije ravnine kažemo da su okomite ako je diedralni kut između njih 90°.
Kut između sigma i epsilon ravnine je 90 stupnjeva, što znači da su ravnine okomite
Navedimo primjere okomitih ravnina.
Zid i strop.

Bočni zid i ploča stola.
Formulirajmo znak okomitosti dviju ravnina:
TEOREM: Ako jedna od dvije ravnine prolazi kroz pravac okomit na drugu ravninu, tada su te ravnine okomite.
Dokažimo ovu značajku.
Pod uvjetom je poznato da pravac AM leži u ravnini α, pravac AM okomita na ravninu β,
Dokažite: ravnine α i β su okomite.
Dokaz:
1) Ravnine α i β sijeku se duž prave AR, dok je AM AR, budući da je AM β po uvjetu, odnosno AM okomita na bilo koji pravac koji leži u ravnini β.
2) Nacrtajmo pravac AT okomit na AP u ravnini β.
Dobivamo kut TAM - linearni kut diedralnog kuta. Ali kut TAM = 90°, budući da MA β. Dakle, α β.

Q.E.D.
Iz znaka okomitosti dviju ravnina imamo važnu posljedicu:
POSLJEDICA: Ravnina okomita na pravu duž koje se sijeku dvije ravnine okomita je na svaku od ovih ravnina.
To jest: ako je α∩β=s i γ s, onda γ α i γ β.
Dokažimo ovu posljedicu: ako je gama ravnina okomita na ravnu crtu c, tada je, zbog paralelizma dviju ravnina, gama okomita na alfu. Slično, gama je okomita na beta.
Preformulirajmo ovaj korolar za diedarski kut:
Ravnina koja prolazi kroz linearni kut diedralnog kuta okomita je na rub i površine ovog diedralnog kuta. Drugim riječima, ako smo konstruirali linearni kut diedralnog kuta, tada je ravnina koja prolazi kroz njega okomita na rub i površine ovog diedralnog kuta.
Zadano: ΔABC, C = 90°, AC leži u ravnini α, kut između ravnina α i ABC = 60°, AC = 5 cm, AB = 13 cm.
Nađi: udaljenost od točke B do ravnine α.

1) Konstruirajmo VC α. Tada je CS projekcija BC na ovu ravninu.
2) BC AS (prema uvjetu), dakle, prema teoremu o tri okomice (TTP), CS AS. Prema tome, VSK je linearni kut diedralnog kuta između ravnine α i ravnine trokuta ABC. To jest, WSC = 60°.
3) Iz ΔBCA prema Pitagorinoj teoremi:
Odgovor VK jednak je 6 korijena od tri cm
Praktična uporaba (primijenjeni karakter) okomitosti dviju ravnina.
Dvije ravne u prostoru nazivaju se okomiti ako je kut između njih 90 o .
riža. 37 |
Okomite linije se mogu sijeći i mogu biti nagnute. Lema. Ako je jedan od dvaju paralelnih pravaca okomit na treći pravac, onda je i drugi pravac također okomit na ovaj pravac. Definicija. Za pravac se kaže da je okomit na ravninu ako je okomit na bilo koji pravac koji leži u ravnini. Također kažemo da je ravnina okomita na pravac a. |
riža. 38 |
Ako je pravac a okomit na ravninu, onda očito siječe ovu ravninu. Doista, ako pravac a ne siječe ravninu, tada bi ležao u ovoj ravnini ili bi bio paralelan s njom. Ali u oba slučaja u ravnini bi postojali pravci koji nisu okomiti na pravac a, na primjer, s njom paralelni, što je nemoguće. Dakle, pravac a siječe ravninu. |
Odnos između paralelnih pravaca i njihova okomitost na ravninu.
Znak okomitosti ravne i ravnine.
Opaske.
- Kroz bilo koju točku u prostoru prolazi ravnina okomita na zadanu liniju, štoviše, jedina.
- Kroz bilo koju točku u prostoru prolazi ravna crta okomita na danu ravninu, i štoviše, samo jedna.
- Ako su dvije ravnine okomite na pravu, onda su paralelne.
Zadaci i testovi na temu "Tema 5. "Okomitost ravne i ravnine."
- Okomitost pravca i ravnine
- Diedarski kut. Okomitost ravnine - Okomitost pravaca i ravnina 10 razred
Lekcije: 1 zadatak: 10 kvizova: 1
- Okomito i koso. Kut između linije i ravnine - Okomitost pravaca i ravnina 10 razred
Lekcije: 2 zadatka: 10 Testovi: 1
- Paralelnost pravaca, pravca i ravnine - Paralelnost pravih i ravnina 10. razred
Lekcije: 1 zadaci: 9 testovi: 1
- Okomite linije - Osnovni geometrijski podaci 7. razred
Lekcije: 1 Zadaci: 17 Testovi: 1
Materijal teme sažima i sistematizira podatke o okomitosti linija koje su vam poznate iz planimetrije. Proučavanje teorema o odnosu paralelnosti i okomitosti pravaca i ravnina u prostoru, kao i gradivo o okomici i kosi, poželjno je kombinirati sa sustavnim ponavljanjem relevantnog gradiva iz planimetrije.
Rješenja gotovo svih računskih problema svode se na primjenu Pitagorinog teorema i njegovih posljedica. U mnogim problemima mogućnost primjene Pitagorinog teorema ili njegovih posljedica opravdava se teoremom o tri okomice ili svojstvima paralelizma i okomitosti ravnina.
Koncept okomitih ravnina
Kada se dvije ravnine sijeku, dobivamo diedralne kutove od $4$. Dva kuta su $\varphi $, a druga dva su $(180)^0-\varphi $.
Definicija 1
Kut između ravnina najmanji je od diedarskih kutova koje čine te ravnine.
Definicija 2
Dvije ravnine koje se sijeku nazivaju se okomiti ako je kut između tih ravnina jednak $90^\circ$ (slika 1).
Slika 1. Okomite ravnine
Znak okomitosti dviju ravnina
Teorem 1
Ako je pravac ravnine okomit na drugu ravninu, tada su te ravnine okomite jedna na drugu.
Dokaz.
Neka su nam zadane ravnine $\alpha $ i $\beta $ koje se sijeku duž pravca $AC$. Neka je pravac $AB$ koja leži u ravnini $\alpha $ okomita na ravninu $\beta $ (slika 2).

Slika 2.
Budući da je pravac $AB$ okomit na ravninu $\beta $, također je okomit na pravac $AC$. Dodatno nacrtajmo pravac $AD$ u ravnini $\beta $, okomitoj na pravac $AC$.
Dobivamo da je kut $BAD$ linearni kut diedralnog kuta jednak $90^\circ$. To jest, prema definiciji 1, kut između ravnina je jednak $90^\circ$, što znači da su te ravnine okomite.
Teorem je dokazan.
Iz ovog teorema slijedi sljedeći teorem.
Teorem 2
Ako je ravnina okomita na pravac duž kojeg se sijeku dvije druge ravnine, onda je i ona okomita na te ravnine.
Dokaz.
Neka su nam zadane dvije ravnine $\alpha $ i $\beta $ koje se sijeku duž ravne $c$. Ravnina $\gamma $ okomita je na pravu $c$ (slika 3.)

Slika 3
Budući da pravac $c$ pripada ravnini $\alpha $, a ravnina $\gamma $ okomita na pravac $c$, tada su prema teoremu 1 ravnine $\alpha $ i $\gamma $ okomite.
Kako pravac $c$ pripada ravnini $\beta $, a ravnina $\gamma $ okomita na pravac $c$, tada su prema teoremu 1 ravnine $\beta $ i $\gamma $ okomite.
Teorem je dokazan.
Za svaki od ovih teorema vrijedi i obrnute tvrdnje.
Primjeri zadataka
Primjer 1
Neka nam je dan pravokutni okvir $ABCDA_1B_1C_1D_1$. Pronađite sve parove okomitih ravnina (slika 5).
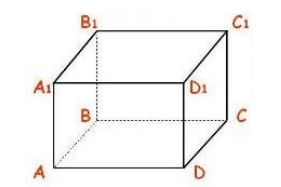
Slika 4
Odluka.
Prema definiciji kockaste i okomite ravnine, vidimo sljedećih osam parova ravnina okomitih jedna na drugu: $(ABB_1)$ i $(ADD_1)$, $(ABB_1)$ i $(A_1B_1C_1)$, $(ABB_1) $ i $(BCC_1) $, $(ABB_1)$ i $(ABC)$, $(DCC_1)$ i $(ADD_1)$, $(DCC_1)$ i $(A_1B_1C_1)$, $(DCC_1)$ i $(BCC_1)$, $(DCC_1)$ i $(ABC)$.
Primjer 2
Neka su nam zadane dvije međusobno okomite ravnine. Iz točke u jednoj ravnini povučena je okomica u drugu ravninu. Dokažite da ovaj pravac leži u zadanoj ravnini.
Dokaz.
Neka su nam $\alpha $ i $\beta $ okomite na ravnine i sijeku se duž ravne $c$. Iz točke $A$ ravnine $\beta $ povučena je okomica $AC$ na ravninu $\alpha $. Pretpostavimo da $AC$ ne leži u ravnini $\beta $ (slika 6).
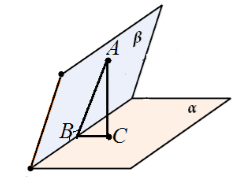
Slika 5
Razmotrimo trokut $ABC$. Pravokutna je s pravim kutom $ACB$. Stoga $\ugao ABC\ne (90)^0$.
Ali, s druge strane, $\ugao ABC$ je linearni kut diedralnog kuta kojeg čine ove ravnine. To jest, diedralni kut koji formiraju ove ravnine nije jednak 90 stupnjeva. Dobivamo da kut između ravnina nije jednak $90^\circ$. Kontradikcija. Stoga $AC$ leži u ravnini $\beta $.
Ova lekcija pomoći će onima koji žele steći ideju o temi "Znak okomitosti dviju ravnina". Na početku ćemo ponoviti definiciju diedralnog i linearnog kuta. Zatim ćemo razmotriti koje se ravnine nazivaju okomitima, te ćemo dokazati kriterij za okomitost dviju ravnina.
Tema: Okomitost pravaca i ravnina
Lekcija: Znak okomitosti dviju ravnina
Definicija. Diedralni kut je lik kojeg čine dvije poluravnine koje ne pripadaju istoj ravnini, a njihova zajednička ravna crta a (a je brid).
Riža. jedan
Razmotrimo dvije poluravnine α i β (slika 1). Zajednička im je granica l. Ova figura naziva se diedralni kut. Dvije ravnine koje se sijeku tvore četiri diedralna kuta sa zajedničkim bridom.
Diedarski kut mjeri se njegovim linearnim kutom. Biramo proizvoljnu točku na zajedničkom bridu l diedralnog kuta. U poluravninama α i β iz ove točke povučemo okomice a i b na pravu l i dobijemo linearni kut diedralnog kuta.
Prave a i b tvore četiri kuta jednaka φ, 180° - φ, φ, 180° - φ. Podsjetimo da se najmanji od ovih kutova naziva kut između linija.
Definicija. Kut između ravnina najmanji je od diedarskih kutova koje čine te ravnine. φ - kut između ravnina α i β, ako
Definicija. Dvije ravnine koje se sijeku nazivaju se okomite (međusobno okomite) ako je kut između njih 90°.

Riža. 2
Na bridu l bira se proizvoljna točka M (slika 2). Povucimo dvije okomite prave MA = a i MB = b na brid l u ravnini α, odnosno u ravnini β. Dobili smo kut AMB. Kut AMB je linearni kut diedralnog kuta. Ako je kut AMB 90°, tada se za ravnine α i β kaže da su okomite.
Pravac b je po konstrukciji okomit na pravac l. Pravac b okomit je na pravac a, budući da je kut između ravnina α i β 90°. Dobivamo da je pravac b okomit na dva pravca a i l koja se sijeku iz ravnine α. Dakle, pravac b okomita na ravninu α.
Slično, može se dokazati da je pravac a okomit na ravninu β. Pravac a je po konstrukciji okomit na pravac l. Pravac a je okomit na pravac b, jer je kut između ravnina α i β 90°. Dobivamo da je pravac a okomit na dva pravca b i l koja se sijeku iz ravnine β. Dakle, pravac a je okomit na ravninu β.
Ako jedna od dvije ravnine prolazi kroz pravac okomit na drugu ravninu, tada su takve ravnine okomite.
Dokazati:

Riža. 3
Dokaz:
Neka se ravnine α i β sijeku duž prave AC (slika 3). Da biste dokazali da su ravnine međusobno okomite, trebate konstruirati linearni kut između njih i pokazati da je taj kut jednak 90 °.
Pravac AB je po uvjetu okomit na ravninu β, a time i na pravac AC koji leži u ravnini β.
Nacrtajmo pravac AD okomit na pravac AC u ravnini β. Tada je BAD linearni kut diedralnog kuta.
Pravac AB okomit je na ravninu β, a time i na pravac AD koji leži u ravnini β. Dakle, linearni kut BAD je 90°. Dakle, ravnine α i β su okomite, što je trebalo dokazati.
Ravnina okomita na pravu duž koje se sijeku dvije zadane ravnine okomita je na svaku od ovih ravnina (slika 4).
Dokazati:

Riža. 4
Dokaz:
Pravac l okomit je na ravninu γ, a ravnina α prolazi kroz pravac l. Dakle, prema kriteriju okomitosti ravnina, ravnine α i γ su okomite.
Pravac l okomit je na ravninu γ, a ravnina β prolazi kroz pravac l. Dakle, prema znaku okomitosti ravnina, ravnine β i γ su okomite.
Predavanje na temu "Znak okomitosti dviju ravnina"
Ideja o ravnini u prostoru omogućuje vam da dobijete, na primjer, površinu stola ili zida. Međutim, stol ili zid imaju konačne dimenzije, a ravnina se proteže izvan njihovih granica u beskonačnost.Razmotrimo dvije ravnine koje se sijeku. Kada se sijeku, tvore četiri diedralna kuta sa zajedničkim rubom.
Prisjetimo se što je diedralni kut.
U stvarnosti se susrećemo s objektima koji imaju oblik diedralnog kuta: na primjer, odškrinuta vrata ili poluotvorena mapa.

Na presjeku dviju ravnina alfa i beta dobivamo četiri diedralna kuta. Neka je jedan od diedarskih kutova jednak (phi), tada je drugi jednak (180 0 -), treći, četvrti (180 0 -).

α iβ, 0°< 90 °
Razmotrimo slučaj kada je jedan od diedarskih kutova jednak 90 0 .
Tada su svi diedralni kutovi u ovom slučaju jednaki 90 0 .
diedralni kut između ravninaα iβ,
90º
Uvedemo definiciju okomitih ravnina:
Za dvije ravnine kažemo da su okomite ako je diedralni kut između njih 90°.
Kut između sigma i epsilon ravnine je 90 stupnjeva, što znači da su ravnine okomite
Jer =90°
Navedimo primjere okomitih ravnina.
Zid i strop.
Bočni zid i ploča stola.

Zid i strop
Formulirajmo znak okomitosti dviju ravnina:
TEOREMA:Ako jedna od dvije ravnine prolazi kroz pravac okomit na drugu ravninu, tada su te ravnine okomite.
Dokažimo ovu značajku.
Po pretpostavci je poznato da je linijaAM leži u ravnini α, pravac AM okomita je na ravninu β,
Dokažite: ravnine α i β su okomite.
Dokaz:
1) Ravnine α iβ sijeku se duž prave AR, dok je AM AR, budući da je AM β po uvjetu, odnosno AM okomito na bilo koji pravac koji leži u ravnini β.
2) Nacrtaj ravnu u ravnini βAT okomitoAR.
Dobivamo kut TAM je linearni kut diedralnog kuta. Ali kut TAM = 90°, budući da MA β. Dakle, α β.
Q.E.D.
TEOREMA:Ako ravnina prolazi kroz pravac okomit na drugu ravninu, tada su te ravnine okomite.

dano:α, β, AM α, AMβ, AM∩=A
Dokazati: αβ.
Dokaz:
1) α∩β = AR, dok je AM AR, budući da je AM β prema uvjetu, to jest, AM okomito na bilo koji pravac koji leži u ravnini β.
2) ATβ,ATAR.
TAM je linearni kut diedralnog kuta. TAM = 90°, jer MA β. Dakle, α β.
Q.E.D
Iz znaka okomitosti dviju ravnina imamo važnu posljedicu:
POSLJEDICA:Ravnina okomita na pravu duž koje se sijeku dvije ravnine okomita je na svaku od ovih ravnina.
Dokažimo ovu posljedicu: ako je gama ravnina okomita na ravnu crtu c, tada je, zbog paralelizma dviju ravnina, gama okomita na alfu. Slično, gama je okomita na beta.

To jest: ako je α∩β=s i γs, onda γα i γβ.
jerγs i sα iz znaka okomitosti γα.
Slično, γ β
Preformulirajmo ovaj korolar za diedarski kut:
Ravnina koja prolazi kroz linearni kut diedralnog kuta okomita je na rub i površine ovog diedralnog kuta. Drugim riječima, ako smo konstruirali linearni kut diedralnog kuta, tada je ravnina koja prolazi kroz njega okomita na rub i površine ovog diedralnog kuta.

Zadatak.
Zadano: ΔABC, C = 90°, AC leži u ravnini α, kut između ravnina α iABC= 60°, AC = 5 cm, AB = 13 cm.
Nađi: udaljenost od točke B do ravnine α.
Odluka:
1) Konstruirajmo VC α. Tada je CS projekcija BC na ovu ravninu.
2) BC AS (prema uvjetu), dakle, prema teoremu o tri okomice (TTP), CS AS. Prema tome, VSK je linearni kut diedralnog kuta između ravnine α i ravnine trokuta ABC. To jest, WSC = 60°.
3) Iz ΔBCA prema Pitagorinoj teoremi:
Od ΔVKS: ![]()


















