4. Examples of constructing Shewhart control charts using GOST R 50779.42–99
Shewhart control charts come in two main types: for quantitative and alternative data. There are two situations for each control chart:
a) standard values are not set;
b) standard values are set.
Standard values– values set according to some specific requirement or purpose.
The purpose of control charts for which standard values are not set is to detect deviations in the values of characteristics (for example, or some other statistics) that are caused by reasons other than those that can only be explained by chance. These control charts are based entirely on the data of the samples themselves and are used to detect variations that are due to non-random causes.
The purpose of control charts, given standard values, is to determine whether the observed values are different, etc. for several subgroups (each with a volume of observations) from the corresponding standard values (or ), etc. more than can be expected from the action of only random causes. A feature of maps with predetermined standard values is an additional requirement related to the position of the center and process variation. The set values can be based on experience gained from using control charts on predetermined standard values, as well as on economic indicators, established after considering the need for the service and the cost of production, or specified in the technical requirements for products.
4.1 Control charts for quantitative data
Control charts for quantitative data are classic control charts used for process control where the characteristics or results of the process are measurable and measured with the required accuracy. actual values controlled parameter are recorded.
Control charts for quantitative data allow you to control both the location of the center (level, average, center of adjustment) of the process, and its spread (range, standard deviation). Therefore, control charts for quantitative data are almost always used and analyzed in pairs, one for location and one for scatter.
The most commonly used are pairs and -cards, as well as -cards. Formulas for calculating the position of the control boundaries of these maps are given in Table. 1. The values of the coefficients included in these formulas and depending on the sample size are given in Table. 2.
It should be emphasized that the coefficients given in this table were obtained on the assumption that the quantitative values of the controlled parameter have a normal or close to normal distribution.
Table 1
Control Limit Formulas for Shewhart Maps Using Quantitative Data
| Statistics | Standard values are set | |||
| central line | UCL and LCL | central line | UCL and LCL | |
| Note: Default values are either , , or . |
||||
table 2
Coefficients for calculating control chart lines
| Number of observations in subgroup n | Coefficients for calculating control limits | Coefficients for calculating the center line | |||||||||||||
| 2 | 2,121 | 1,880 | 2,659 | 0,000 | 3,267 | 0,000 | 2,606 | 0,000 | 3,686 | 0,000 | 3,267 | 0,7979 | 1,2533 | 1,128 | 0,8865 |
| 3 | 1,732 | 1,023 | 1,954 | 0,000 | 2,568 | 0,000 | 2,276 | 0,000 | 4,358 | 0,000 | 2,574 | 0,8886 | 1,1284 | 1,693 | 0,5907 |
| 4 | 1,500 | 0,729 | 1,628 | 0,000 | 2,266 | 0,000 | 2,088 | 0,000 | 4,696 | 0,000 | 2,282 | 0,9213 | 1,0854 | 2,059 | 0,4857 |
| 5 | 1,342 | 0,577 | 1,427 | 0,000 | 2,089 | 0,000 | 1,964 | 0,000 | 4,918 | 0,000 | 2,114 | 0,9400 | 1,0638 | 2,326 | 0,4299 |
| 6 | 1,225 | 0,483 | 1,287 | 0,030 | 1,970 | 0,029 | 1,874 | 0,000 | 5,078 | 0,000 | 2,004 | 0,9515 | 1,0510 | 2,534 | 0,3946 |
| 7 | 1,134 | 0,419 | 1,182 | 0,118 | 1,882 | 0,113 | 1,806 | 0,204 | 5,204 | 0,076 | 1,924 | 0,9594 | 1,0423 | 2,704 | 0,3698 |
| 8 | 1,061 | 0,373 | 1,099 | 0,185 | 1,815 | 0,179 | 1,751 | 0,388 | 5,306 | 0,136 | 1,864 | 0,9650 | 1,0363 | 2,847 | 0,3512 |
| 9 | 1,000 | 0,337 | 1,032 | 0,239 | 1,761 | 0,232 | 1,707 | 0,547 | 5,393 | 0,184 | 1,816 | 0,9693 | 1,0317 | 2,970 | 0,3367 |
| 10 | 0,949 | 0,308 | 0,975 | 0,284 | 1,716 | 0,276 | 1,669 | 0,687 | 5,469 | 0,223 | 1,777 | 0,9727 | 1,0281 | 3,078 | 0,3249 |
| 11 | 0,905 | 0,285 | 0,927 | 0,321 | 1,679 | 0,313 | 1,637 | 0,811 | 5,535 | 0,256 | 1,744 | 0,9754 | 1,0252 | 3,173 | 0,3152 |
| 12 | 0,866 | 0,266 | 0,886 | 0,354 | 1,646 | 0,346 | 1,610 | 0,922 | 5,594 | 0,283 | 1,717 | 0,9776 | 1,0229 | 3,258 | 0,3069 |
| 13 | 0,832 | 0,249 | 0,850 | 0,382 | 1,618 | 0,374 | 1,585 | 1,025 | 5,647 | 0,307 | 1,693 | 0,9794 | 1,0210 | 3,336 | 0,2998 |
| 14 | 0,802 | 0,235 | 0,817 | 0,406 | 1,594 | 0,399 | 1,563 | 1,118 | 5,696 | 0,328 | 1,672 | 0,9810 | 1,0194 | 3,407 | 0,2935 |
| 15 | 0,775 | 0,223 | 0,789 | 0,428 | 1,572 | 0,421 | 1,544 | 1,203 | 5,741 | 0,347 | 1,653 | 0,9823 | 1,0180 | 3,472 | 0,2880 |
| 16 | 0,750 | 0,212 | 0,763 | 0,448 | 1,552 | 0,440 | 1,526 | 1,282 | 5,782 | 0,363 | 1,637 | 0,9835 | 1,0168 | 3,532 | 0,2831 |
| 17 | 0,728 | 0,203 | 0,739 | 0,466 | 1,534 | 0,458 | 1,511 | 1,356 | 5,820 | 0,378 | 1,622 | 0,9845 | 1,0157 | 3,588 | 0,2784 |
| 18 | 0,707 | 0,194 | 0,718 | 0,482 | 1,518 | 0,475 | 1,496 | 1,424 | 5,856 | 0,391 | 1,608 | 0,9854 | 1,0148 | 3,640 | 0,2747 |
| 19 | 0,688 | 0,187 | 0,698 | 0,497 | 1,503 | 0,490 | 1,483 | 1,487 | 5,891 | 0,403 | 1,597 | 0,9862 | 1,0140 | 3,689 | 0,2711 |
| 20 | 0,671 | 0,180 | 0,680 | 0,510 | 1,490 | 0,504 | 1,470 | 1,549 | 5,921 | 0,415 | 1,585 | 0,9869 | 1,0133 | 3,735 | 0,2677 |
| 21 | 0,655 | 0,173 | 0,663 | 0,523 | 1,477 | 0,516 | 1,459 | 1,605 | 5,951 | 0,425 | 1,575 | 0,9876 | 1,0126 | 3,778 | 0,2647 |
| 22 | 0,640 | 0,167 | 0,647 | 0,534 | 1,466 | 0,528 | 1,448 | 1,659 | 5,979 | 0,434 | 1,566 | 0,9882 | 1,0119 | 3,819 | 0,2618 |
| 23 | 0,626 | 0,162 | 0,633 | 0,545 | 1,455 | 0,539 | 1,438 | 1,710 | 6,006 | 0,443 | 1,557 | 0,9887 | 1,0114 | 3,858 | 0,2592 |
| 24 | 0,612 | 0,157 | 0,619 | 0,555 | 1,445 | 0,549 | 1,429 | 1,759 | 6,031 | 0,451 | 1,548 | 0,9892 | 1,0109 | 3,895 | 0,2567 |
| 25 | 0,600 | 0,153 | 0,606 | 0,565 | 1,434 | 0,559 | 1,420 | 1,806 | 6,056 | 0,459 | 1,541 | 0,9896 | 1,0105 | 3,931 | 0,2544 |
An alternative to maps are median control maps (– maps), which are less computationally intensive than maps. This can facilitate their introduction into production. The position of the central line on the map is determined by the average value of the medians () for all controlled samples. The positions of the upper and lower control boundaries are determined by the relations
 (4.1)
(4.1)
The values of the coefficient depending on the sample size are given in Table. 3.
Table 3
Coefficient values
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1,88 | 1,19 | 0,80 | 0,69 | 0,55 | 0,51 | 0,43 | 0,41 | 0,36 |
Usually – map is used together with – map, sample size
In some cases, the cost or duration of the measurement of the controlled parameter is so great that it is necessary to control the process based on the measurement of individual values of the controlled parameter. In this case, the sliding range serves as a measure of process variation, i.e. the absolute value of the difference between the measurements of the controlled parameter in successive pairs: the difference between the first and second measurements, then the second and third, etc. Based on the moving ranges, the average moving range is calculated, which is used to build control charts of individual values and moving ranges (and -maps). Formulas for calculating the position of the control boundaries of these maps are given in Table. 4.
Table 4
Control Limit Formulas for Individual Value Maps
| Statistics | Standard values are not set | Standard values are set | ||
| central line | UCL and LCL | central line | UCL and LCL | |
| individual value | ||||
| Sliding | ||||
| Note: Standard values and or and are set. |
||||
The values of the coefficients and can be obtained indirectly from Table 2 at n=2.
4.1.1 and -cards. Standard values are not set
In table. 6 shows the results of measurements of the outer radius of the sleeve. Four measurements were taken every half an hour, for a total of 20 samples. The averages and ranges of subgroups are also given in Table. 5. Fitted to the limit allowed values outer radius: 0.219 and 0.125 dm. The goal is to determine the performance of the process and control it by tuning and dispersion so that it corresponds to established requirements.
Table 5
Production data for bushing outside radius
| Subgroup number | Radius | |||||
| 1 | 0,1898 | 0,1729 | 0,2067 | 0,1898 | 0,1898 | 0,038 |
| 2 | 0,2012 | 0,1913 | 0,1878 | 0,1921 | 0,1931 | 0,0134 |
| 3 | 0,2217 | 0,2192 | 0,2078 | 0,1980 | 0,2117 | 0,0237 |
| 4 | 0,1832 | 0,1812 | 0,1963 | 0,1800 | 0,1852 | 0,0163 |
| 5 | 0,1692 | 0,2263 | 0,2066 | 0,2091 | 0,2033 | 0,0571 |
| 6 | 0,1621 | 0,1832 | 0,1914 | 0,1783 | 0,1788 | 0,0293 |
| 7 | 0,2001 | 0,1937 | 0,2169 | 0,2082 | 0,2045 | 0,0242 |
| 8 | 0,2401 | 0,1825 | 0,1910 | 0,2264 | 0,2100 | 0,0576 |
| 9 | 0,1996 | 0,1980 | 0,2076 | 0,2023 | 0,2019 | 0,0096 |
| 10 | 0,1783 | 0,1715 | 0,1829 | 0,1961 | 0,1822 | 0,0246 |
| 11 | 0,2166 | 0,1748 | 0,1960 | 0,1923 | 0,1949 | 0,0418 |
| 12 | 0,1924 | 0,1984 | 0,2377 | 0,2003 | 0,2072 | 0,0453 |
| 13 | 0,1768 | 0,1986 | 0,2241 | 0,2022 | 0,2004 | 0,0473 |
| 14 | 0,1923 | 0,1876 | 0,1903 | 0,1986 | 0,1922 | 0,0110 |
| 15 | 0,1924 | 0,1996 | 0,2120 | 0,2160 | 0,2050 | 0,0236 |
| 16 | 0,1720 | 0,1940 | 0,2116 | 0,2320 | 0,2049 | 0,0600 |
| 17 | 0,1824 | 0,1790 | 0,1876 | 0,1821 | 0,1828 | 0,0086 |
| 18 | 0,1812 | 0,1585 | 0,1699 | 0,1680 | 0,1694 | 0,0227 |
| 19 | 0,1700 | 0,1567 | 0,1694 | 0,1702 | 0,1666 | 0,0135 |
| 20 | 0,1698 | 0,1664 | 0,1700 | 0,1600 | 0,1655 | 0,0100 |
![]()
![]()
where is the number of subgroups,
The first step: building a map and determining the state of the process from it.
central line:
The values of the factors and are taken from Table. 2 for n=4. Since the values in Table. 5 are within the control limits, the map indicates a statistically controlled state. The value can now be used to calculate map control boundaries.
center line: g
The multiplier values are taken from Table. 2 for n=4.
and -maps are shown in Fig. 5. Analysis of the map shows that the last three points are out of bounds. This indicates the possibility of some special causes of variation being at work. If limits have been calculated from previous data, then action must be taken at the point corresponding to the 18th subgroup.

Fig.5. Medium and Span Cards
At this point in the process, appropriate corrective action should be taken to eliminate special causes and prevent recurrence. The work with the maps continues after the establishment of the revised control boundaries without excluded points that have gone beyond the old boundaries, i.e. values for samples no. 18, 19 and 20. The values and lines of the control chart are recalculated as follows:
revised value ![]()
revised value ![]()
the revised map has following parameters:
center line: g
revised map:
central line:
(because the central line: , then there is no LCL).
For a stable process with revised control limits, the possibilities can be assessed. We calculate the index of opportunities:
where is the upper limit value of the controlled parameter; – lower limit value of the controlled parameter; - estimated by the average variability within subgroups and expressed as . The value of the constant is taken from table 2 for n=4.

Rice. 6. Revised and -maps

Since , the possibilities of the process can be considered acceptable. However, upon close examination, it can be seen that the process is not set up correctly in relation to the tolerance and therefore about 11.8% of the units will be outside the set upper limit value. Therefore, before setting the constant parameters of the control charts, one should try to set up the process correctly, while maintaining it in a statistically controlled state. 

The tool is used when processing is carried out with a tool whose design and dimensions are approved by GOST and OST or are available in industry standards. When developing technological processes for manufacturing parts, a normalized tool should be used as the cheapest and easiest. Special cutting tool used in cases where processing is normalized ...





Such control is very expensive. Therefore, from continuous control, they pass to selective with the use of statistical methods for processing the results. However, such control is effective only when the technological processes, being in an established state, have the accuracy and stability sufficient to “automatically” guarantee the manufacture of defect-free products. Hence the need...




And the organization of the control process. Control status In this course project terms of reference the development of the stages of the process of acceptance control of the part of the gearbox of a cylindrical coaxial two-stage two-flow gearbox - a gear wheel and active control of the hole grinding operation is envisaged. The methods of active and acceptance control complement each other and are combined. Active...
Plan:
10.1 Basics of Shewhart's Control Charts
10.2 Types of Shewhart control charts
10.1 Basics of Shewhart's Control Charts
The task of statistical process control is to ensure and maintain processes at an acceptable and stable level, ensuring that products and services meet specified requirements. The main statistical tool used for this is the control chart. The control chart method helps to determine whether the process has indeed reached or remains in a statistically controlled state at the right level, and then to maintain control and a high degree of uniformity of the most important characteristics of the product or service by continuously recording information about the quality of the product during the production process. The use of control charts and their careful analysis lead to a better understanding and improvement of processes.
Shewhart Control Charts (CCC) are the main tool of statistical quality management. The CCF is used to compare the information obtained from the samples about the current state of the process with the control limits, which represent the limits of the intrinsic variability (scatter) of the process. The KKH is used to assess whether or not a manufacturing process, service process, or management process is in a statistically controlled state. Initially, KKSH were developed for use in industrial production. Currently, they are widely used in the service industry and other areas.
Control card is a graphical way of presenting and comparing information based on a sequence of samples reflecting the current state of a process, with boundaries set based on the intrinsic variability of the process.
Control chart theory distinguishes between two kinds of variability. The first type is variability due to “random (ordinary variables) due to an innumerable set of diverse causes that are constantly present, which are not easy or impossible to detect. Each of these causes constitutes a very small fraction of the total variability, and none of them is significant on its own. However, the sum of all these causes is measurable and is assumed to be intrinsic to the process. Eliminating or reducing the impact of common causes requires management decisions and the allocation of resources to improve the process and system. The second kind is real change in the process. They may be the result of some identifiable causes that are not inherent in the process internally, and can be eliminated. These identifiable causes are considered as "non-random" or "special" causes of change. These may include tool breakage, insufficient homogeneity of material, production or control equipment, qualification of personnel, failure to follow procedures, etc.
The purpose of control charts is to detect unnatural changes in data from repetitive processes and provide criteria for detecting a lack of statistical control. A process is in a statistically controlled state if the variability is caused only by random causes. When determining this acceptable level of variability, any deviation from it is considered the result of special causes that should be identified, eliminated or reduced.
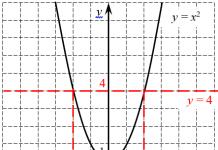
The Shewhart map requires data to be sampled from the process at roughly equal intervals. Intervals can be set either by time (eg hourly) or by quantity (each batch). Typically, each sub-group consists of the same type of product or service with the same controlled indicators, and all sub-groups have equal volumes. For each subgroup, one or more characteristics are determined, such as the arithmetic mean of the subgroup and the range of the subgroup R or the sample standard deviation S. The Shewhart map is a graph of the values of certain characteristics of the subgroups depending on their numbers. It has a center line (CL) corresponding to the characteristic reference value. When assessing whether a process is in a statistically controlled state, the reference is usually the arithmetic mean of the data under consideration. In process control, the reference value is the long-term characteristic value set in specifications, or its nominal value based on previous information about the process, or the intended target value of a product or service characteristic. The Shewhart map has two statistically defined control limits about the center line, called the upper control limit (UCL) and the lower control limit (LCL) (Figure 9).
Sequence number of the sample
Figure 9 - View of the control chart
The control lines on Shewhart's map are at a distance of 3  from the center line where
from the center line where  is the general standard deviation of the statistics used. Variation within subgroups is a measure of random variation. To get an estimate
is the general standard deviation of the statistics used. Variation within subgroups is a measure of random variation. To get an estimate  calculate the sample standard deviation or multiply the sample range by the appropriate factor. This measure does not include intergroup variation, but only assesses variation within subgroups.
calculate the sample standard deviation or multiply the sample range by the appropriate factor. This measure does not include intergroup variation, but only assesses variation within subgroups.
Limits ±3  indicate that about 99.7% of the values of the characteristics of the subgroups will fall within these limits, provided that the process is in a statistically controlled state. In other words, there is a risk equal to 0.3% (or an average of three in a thousand cases) that the plotted point will be outside the control limits when the process is stable. The word "approximately" is used because deviations from initial assumptions, such as the distribution of the data, will affect the probability values.
indicate that about 99.7% of the values of the characteristics of the subgroups will fall within these limits, provided that the process is in a statistically controlled state. In other words, there is a risk equal to 0.3% (or an average of three in a thousand cases) that the plotted point will be outside the control limits when the process is stable. The word "approximately" is used because deviations from initial assumptions, such as the distribution of the data, will affect the probability values.
Some consultants prefer 3.09 instead of a factor of 3 to provide a nominal probability of 0.2% (an average of two misleading observations per thousand), but Shewhart chose 3 to avoid considering exact probabilities. Similarly, some consultants use actual probabilities for maps based on non-normal distributions, such as range and disparity maps, in which case the Shewhart map also uses boundaries at a distance of ± 3  instead of probabilistic limits, simplifying the empirical interpretation.
instead of probabilistic limits, simplifying the empirical interpretation.
The probability that a boundary violation is indeed a random event, and not a real signal, is considered so small that when a point outside the boundaries appears, certain actions should be taken. Since the action is taken at this point, then  control boundaries are sometimes referred to as "action boundaries".
control boundaries are sometimes referred to as "action boundaries".
Often on the control map, the boundaries are also drawn at a distance of 2  .Then any sample value that falls outside the boundaries of 2a can serve as a warning about the imminent situation of the process exiting the state of statistical controllability. Therefore, the limits ±2
.Then any sample value that falls outside the boundaries of 2a can serve as a warning about the imminent situation of the process exiting the state of statistical controllability. Therefore, the limits ±2  sometimes called "warning".
sometimes called "warning".
When using control charts, two types of errors are possible: the first and second kind.
A Type I error occurs when the process is in a statistically controlled state and the point jumps out of control bounds by accident. As a result, it is incorrectly determined that the process is out of statistical control and an attempt is made to find and eliminate the cause of a non-existent problem.
A Type II error occurs when the process in question is out of control and the points happen to be inside the control boundaries. In this case, they incorrectly conclude that the process is statistically controlled and miss the opportunity to prevent an increase in the yield of nonconforming products. Type II error risk is a function of three factors: the width of the control limits, the degree of uncontrollability, and the sample size. Their nature is such that only a general statement about the magnitude of the error can be made.
The Shewhart charting system takes into account only Type I errors of 0.3% within bounds 3  . Since it is generally impractical to make a full estimate of the losses from a Type II error in specific situation, while it is convenient to arbitrarily take a small volume of the subgroup (4 or 5 units), it is advisable to use boundaries at a distance of ± 3
. Since it is generally impractical to make a full estimate of the losses from a Type II error in specific situation, while it is convenient to arbitrarily take a small volume of the subgroup (4 or 5 units), it is advisable to use boundaries at a distance of ± 3  and focus mainly on managing and improving the quality of the process itself.
and focus mainly on managing and improving the quality of the process itself.
If the process is statistically controlled, the control charts implement a method of continuous statistical testing of the null hypothesis that the process has not changed and remains stable. But since the value of a particular deviation of a process characteristic from the target that could attract attention can usually not be determined in advance, as well as the risk of a type II error, and the sample size is not calculated to satisfy the corresponding level of risk, the Shewhart map should not be considered from the point of view of testing hypotheses. . Shewhart emphasized the empirical utility of control charts in establishing deviations from the state of statistical control, and not their probabilistic interpretation. Some users use performance curves as a means of interpreting hypothesis tests.
When the plotted value is outside any of the control limits, or the series of values exhibits unusual patterns, the state of statistical control is questioned. In this case, it is necessary to investigate and detect non-random (special) causes, and the process can be stopped or corrected. Once special causes are found and ruled out, the process is ready to continue again. When a Type I error occurs, no particular cause can be found. Then it is believed that the point going beyond the boundaries is a rather rare random phenomenon when the process is in a statistically controlled state.
When a process control chart is built for the first time, it often turns out that the process is statistically uncontrollable. Control limits calculated from data from such a process will sometimes lead to erroneous conclusions because they may be too wide. Therefore, before setting the constant parameters of the control charts, it is necessary to bring the process into a statistically controlled state.
SAINT PETERSBURG STATE UNIVERSITY
FACULTY OF ECONOMICS
Department of Economics and Management at the Enterprise
Shewhart control charts in the quality management system
Course work
2nd year students of the EUP group - 22
day department
specialty 080502 - "Economics and management at the enterprise"
Supervisor:
Saint Petersburg
Introduction
Chapter 1. The concept of a quality management system
Chapter 2. Importance of statistical methods in quality management
Chapter 2.1. Shewhart control charts as a method of statistical control and quality management
Chapter 3
Conclusion
Literature
Appendix 1
The peak of development of quality management fell on 1980-1990, when the quality management system was widely introduced. Early in its development, the concept helped many companies rethink their manufacturing process and avoid the multi-million dollar costs associated with manufacturing defective products.
In parallel with reducing defects and improving product quality, companies began to pay more attention to consumers and their desires. After all, as you know, attracting a new client can cost 6 times more than a company than retaining an existing one.
On the early stages From its inception, quality management was not much different from careful administration or dispatching, but as time went on, the theory developed and the practice of applying the concept expanded. Now, not only industrial, but also service companies practice a qualitative approach and use modern facilities quality control; usually it is automated systems(ERP, MRP, process control systems), which have in their arsenal applications for building diagrams, maps, accounting for the number of defects, or simply convenient organization of customer data (CRM).
The purpose of this work is to systematize knowledge in the field of quality management. This is what gave rise to the structure. term paper, to consider the historical aspects of the development of the concept, the first chapter is allotted; a description of the significance of statistical methods - the second chapter; and the construction of control charts, on the example of a random sample of some process - in the third. The consideration of Shewhart's control charts, and not other, later developments, is explained, first of all, by the fact that Shewhart's work gave impetus to the development of the concept in this direction. And for a deeper understanding of the entire quality management, it is necessary to have knowledge about the emergence of significant discoveries.
Quality management has many definitions, depending on the position taken by the author. Some emphasize the special role of the human factor, others emphasize the importance systems approach and quantitative measurements, others emphasize the evolution of management schools.
So, quality management is, in a broad sense, such enterprise management that allows you to most fully meet the needs of customers and anticipate their expectations. Natural, in my opinion, questions arise: firstly, how is their satisfaction carried out, and secondly, how does the quality management approach in this regard differ from the usual process of planning and manufacturing products?
Answering the question about customer satisfaction, we can say that quality management takes the attitude of the consumer to the quality of the products received as the main condition. In this case, product quality becomes the most significant indicator for the consumer and, as a result, the main competitive advantage.
The second question concerns the differences between conventional production and one where the principles of quality are applied. The position of Japanese authors is interesting, relating the process of product quality management to a special philosophy of the enterprise, a new look at production and inextricably linked with the concept of continuous improvement. Besides this slightly idealized attitude, another difference can be shown; the normal production process involves a series of activities aimed at identifying and meeting the needs of consumers, which is also referred to in the definition of quality management. However, the quality approach emphasizes the inherent importance of manufacturing quality products, at all stages of production, from product development to timely delivery to the consumer. This approach dictates the priority task facing the enterprise - the manufacture of high-quality products from cycle to cycle, which undoubtedly guarantees the stability of the consumer receiving good products. For the enterprise, this, first of all, means gaining the respect of consumers and developing their loyalty, which in modern conditions, is by no means an unimportant feature.
Summing up, we see that consumers receive quality products, and manufacturers receive stable profits. Modern Markets show a rapid pace of development, which sets the condition for firms: "develop to survive." And in this case, a good, high-quality product, but not meeting the requirements of the market, will also not be able to provide significant competition, just like a company whose 30% of its products are defective goods. That is why quality management assigns an important role to anticipating the expectations and needs of the consumer, creating new needs for him and satisfying them, in accordance with the approach of ensuring product quality.
As shown above, quality management is an extensive process, and affects all production, all levels of management (from controllers to managers). top management) and all production processes. But where and under what conditions did it originate? What contributed to the emergence of a new approach to management? Let's look at quality management in retrospect.
Product quality management is a red line that runs through the entire history of management development. Beginning with Towne's famous 1866 work, "The Engineer as Economist," it is customary to talk about the birth of management.
Inspired by the work of Town, the founder of the scientific school of management was F. Taylor. His approach literally revolutionized production. In addition to introducing the practice of measuring the time spent on performing various operations, Taylor established requirements for the quality of products, in the form of tolerance fields (through and non-through calibers). He also established a system of fines for marriage (up to dismissal), motivation and training of employees. Taylor's revolutionary approach gave impetus to the further development of management.
Another notorious manager of the 20th century was Henry Ford, who founded the car company that still exists today. By developing the Model T, Ford doomed himself to perpetuate. He not only invented a light, durable (at that time) and unpretentious car, but also introduced a system of mass conveyor production. He unified and standardized all operations, included after-sales service in the scope of production. Engaged in labor protection and the creation of normal working conditions. “According to Henry Ford, the main factor in the success of an enterprise is quality product which it produces. Until the quality is proven, the production of the product cannot be started.
Emerson made a major contribution to the development of management, with a book published in 1912, The 12 Principles of Productivity. Emerson noted the importance of goal setting, scheduling, performance rewards, and other principles. He saw efficiency as a key aspect of the organization of production, by increasing which it is possible to achieve high results, avoiding overstrain.
During further development management of the enterprise faced the need to reduce labor costs for quality control, since the old methods of quality control, which involved the control of each unit of output, led to the growth of the staff of controllers. The problem was solved by the methods that replaced them - the methods of statistical quality control. G. Dodge and G. Roming proposed sampling methods that made it possible to check not all products, but a certain amount from the entire batch. Statistical control was carried out by new specialists - quality engineers.
A great contribution to the application of statistical methods belongs to Walter Shewhart, who, while working at Bell's company (Bell Telephone Laboratories, now AT & T) as part of a group of quality specialists, in the mid-1920s. laid the foundation for statistical quality control. Shewhart is listed among the patriarchs modern philosophy quality . Shewhart devoted much attention to the compilation and analysis of control charts, which will be discussed in subsequent chapters.
The contribution of Edward Deming, an American specialist in the field of quality, is great. During World War II, he trained US engineers in quality control as part of the national defense program. After the war, in 1950, Deming was invited to occupied Japan to present a joint theory with Shewhart. Speaking to the owners and managers of most enterprises, Deming exhorted that if statistical methods were followed, then very soon Japanese manufacturers would be able to enter world markets. Which was vital to post-war Japan.
Deming's teachings set the direction for the development of Japanese companies. Deming, inspired the audience with his ideas, "no nation is obliged to be poor" was his opening phrase. Very soon, Japan entered the world markets, with goods superior in quality to their American and European counterparts.
The next scientist to come to Japan from America was Juran. Juran considered quality issues at the level of the entire company and individual departments. Juran's lectures were of a practical nature, and the emphasis was placed on determining the indicators of quality products, setting standards and methods of measurement, and conformity of products to specifications.
The goal of a quality approach is to create a better product that can better meet the needs of customers. And such difficult problem cannot be solved by only taking the necessary measurements and analyzing the data obtained. To achieve such a goal, it is sometimes necessary to modernize existing equipment, improve the technological process of production, or completely change it. It is also worth considering necessary work up to ( marketing research, design, procurement) and after (packaging, storage, supply, sales and after-sales service) production of products. All this proves the need to consider quality management in unified system and manage it with a single enterprise-wide strategy.
In parallel with Deming and Juran, Dr. Feigenbaum (USA), in the 50s, in the monograph "Total Quality Management" outlines the importance of a systematic (complex) approach to product quality management.
In 1922, an expert group from the United States introduced the concept of Total Quality: “Total quality (TQ) is a management system focused on people, the goal of which is to constantly increase the degree of customer satisfaction while constantly reducing real costs. TQ is a system-wide approach (rather than individual sites or programs) and an integral part of the strategy top level; it works horizontally, spanning functions and departments, engaging all employees from the top down and transcending traditional boundaries to include the overall supply chain and, ultimately, the customer chain. In TQ big influence is given to mastering the policy of constant change and its adaptation, since these components are considered powerful levers that significantly affect the success of the organization.
The next step in the development of a quality management system is the development of a process approach and the popularization of reengineering. Reengineering proposes to replace the principle of division of labor in management with a process approach. At the head of the organization are processes that have their own performers. Enterprises were embraced by a new idea, a massive review of the work of processes began, their optimization, change and implementation of new ones. Until it was discovered that reengineering is by no means a universal remedy.
Now, in the 21st century, an adaptive model of organization is taking root in science and the concept of knowledge management is spreading.
But, despite the widespread knowledge of quality management methods and systems, many enterprises do not realize the importance of quality control. In an effort to keep up with world standards, establish software products, build control charts, not understanding how it can help them.
No matter how simple or complex the methods of quality management are, by themselves they will not be able to provide any benefit to the enterprise, because, even after conducting all the necessary research and receiving conclusions, it is still necessary to develop and implement changes. A significant part of Russian enterprises, starting to develop a quality management system (QMS), does not set the task of achieving effectiveness, and even more so, the effectiveness of the QMS, which is prerequisite quality management. The implementation of the widespread ISO system is more like an expensive certification than a management aimed at satisfying consumers.
The introduction of total quality management in Russia is associated with significant difficulties, and above all, this is the rejection of the concept of quality by managers, the unwillingness to be leaders committed to the implementation of quality and to follow the chosen goal. The specificity of Russia, its people, customs and practices, apparently, will not soon be ready for cardinal changes in the system of views on the management of the organization.
These are the main milestones in the development of product quality management systems.
map shewhart quality control
The value of statistical methods can hardly be overestimated, since without such methods of control, it would be difficult, almost impossible, to identify the dependence of defects on certain factors. At the same time, organizations should strive to reduce the variability of factors, and as a result, the manifestation of greater stability in product quality. For example, during machining metal, a cutter is used, which, after processing a new unit of metal, becomes a little dull. In addition, changes in temperature, coolant composition, or other influences can lead to product defects.
Not all factors involved in production are stable, and statistical methods of quality control and management are aimed at reducing their variability. There are, however, other ways to reduce the level of product defects, such as using expert intuition or past experience to eliminate such problems.
The proposed methods can either be very effective or fail to correctly diagnose and solve the problem. And here it is up to the person who manages the control, the conformity of methods to achieve the goals of the study, the objectivity of the selected indicators, the reliability of measurements, etc.
Let's consider statistical methods of quality control. Kaeru Ishikawa, professor emeritus at the University of Tokyo, proposed the division of statistical methods into three groups:
1. elementary methods, these include "seven simple quality tools"
control sheet
æ allows you to conveniently record data on defects that the controller encounters. In the future, it becomes a source of statistical information.
quality histogram
æ It is built on the basis of a control sheet and shows the frequency of the values of the controlled parameter falling within the specified intervals.
causal diagram
æ is also called a fishbone diagram. The diagram is based on one quality indicator, which takes the form of a straight horizontal line (“backbone”), to which the main causes that affect the indicator (“big bones of the ridge”) are joined by lines. Secondary and tertiary causes that influence the older causes are also connected by straight lines (“medium and small bones”). After construction, it is necessary to rank all the reasons according to the degree of influence on the indicator.
Pareto chart
æ The main assumption of the diagram is that in most cases, the vast majority of defects arise from a small number of important causes. The consequence of the sharpened diagram will be the conclusion about what types of defects have a large share among the rest and, accordingly, what should be paid special attention to.
·Stratification
æ Data stratification or stratification is carried out when it is necessary to compare the results of similar processes performed by different workers, or on different machines, using different materials and in other cases.
scatter diagram
æ is built on the basis of paired data (for example, the number of defects on the air temperature in the furnace), the dependence of which must be investigated. The diagram can give information about the shape of the distribution of pairs. Based on the diagram, it is possible to carry out correlation and regression analysis.
control card
æ principles and methods of constructing control charts will be discussed in the third chapter of the work.
2. intermediate methods, these are acceptance control methods, distribution theories, statistical estimates and criteria.
3. advanced methods, these are methods based on the use of computer technology:
experiment planning,
multivariate analysis
· methods of research of operations.
Product quality is determined by a set of quantities and features, which in general can be called quality indicators. On their basis, statistical studies are carried out. The indicators characterize the consumer properties of products and may have different meaningful meanings.
Control cards belong to the "seven simple methods» quality management, according to the classification of K. Ishikawa. Like other methods, control charts are aimed at identifying factors that affect the variability of processes. Since, variability can be influenced by random or certain (non-random) reasons. Random causes can be attributed to such causes, whose occurrence cannot be avoided, even using the same raw materials, equipment and workers serving the process (for example, temperature fluctuations environment, material characteristics, etc.). Certain (non-random) reasons imply the presence of some dependence between the change in factors and the variability of the process. Such reasons can be identified and eliminated during process tuning (for example, loosening of fasteners, tool wear, insufficient sharpening of the machine, etc.). Ideally, the variability of certain factors should be reduced to zero, and by improving technological process to reduce the influence and random factors.
Control charts are used to adjust already existing processes in which the products meet the technical requirements.
The construction of control charts is mainly aimed at confirming or rejecting the hypothesis about the stability and controllability of the process. Due to the fact that the maps are of a multiple nature, they allow you to determine whether the course of the process under study is random, if so, then the process should tend to a normal, Gaussian distribution. Otherwise, trends, series and other abnormal deviations can be traced on the chart.
The next chapter will deal with the practical side of Shewhart's control charts.
Before proceeding to the direct construction of control charts, let's get acquainted with the main stages of the task. So, in view of the fact that different authors pursue their own goals, describing the construction of control charts, the original vision of the stages of construction of Shewhart's control charts will be presented below.
Algorithm for constructing Shewhart control charts:
I. Process analysis.
First of all, it is necessary to ask a question about the existing problem, because, in the absence of these, the analysis will not make sense. For greater clarity, you can use the cause-and-effect diagram of Ishikawa (mentioned above, ch. 2). To compile it, it is recommended to involve employees from different departments and use brainstorming. After a thorough analysis of the problem, and finding out the factors influencing it, we proceed to the second stage.
II. Process selection.
Having clarified in the previous stage the factors influencing the process, having drawn a detailed skeleton of the “fish”, it is necessary to choose the process that will be subject to further research. This step is very important because choosing the wrong indicators will make the whole control chart less effective due to the examination of insignificant indicators. At this stage, it is worth realizing that the choice of the appropriate process and indicator determines the outcome of the entire study and the costs associated with it.
Here are some examples of possible indicators:
Table 1. The use of control cards in service organizations
Source Evans J. Quality Management: textbook. Allowance/J. Evans.-M.: Unity-Dana, 2007.
At the same time, the indicator should be chosen, guided by the main goal of the company, namely, customer satisfaction. When the process and the indicator that characterizes it are selected, you can proceed to data collection.
III. Data collection.
The purpose of this stage is to collect data about the process. To do this, it is necessary to design the most suitable way to collect data, find out who and at what time will take measurements. If the process is not equipped technical means, allowing to automate the entry and processing of data, it is possible to use one of the seven simple ways Ishikawa - control sheets. Control sheets, in fact, are forms for registering the parameter under study. Their advantage lies in ease of use and ease of training employees. If there is a computer at the workplace, it is possible to enter data through the appropriate software products.
Depending on the specifics of the indicator, the frequency, time of collection and sample size are determined to ensure representativeness of the data. The collected data is the basis for further operations and calculations.
After collecting information, the researcher must decide on the need to group the data. Grouping often determines the performance of control charts. Here, with the help of the analysis already carried out using the cause-and-effect diagram, it is possible to establish factors by which it will be possible to group the data in the most rational way. It should be noted that data within one group should have little variability, otherwise the data may be misinterpreted. Also, if the process is divided into parts using stratification, each part should be analyzed separately (example: the manufacture of the same parts by different workers).
Changing the way grouping will change the factors that form within-group variation. Therefore, it is necessary to study the factors influencing the change in the indicator in order to be able to apply the correct grouping.
IV. Calculation of control chart values.
Shewhart's control charts are divided into quantitative and qualitative (alternative) depending on the measurability of the studied indicator. If the value of the indicator is measurable (temperature, weight, size, etc.), maps of the value of the indicator, ranges and double maps of Shewhart are used. On the contrary, if the indicator does not allow the use of numerical measurements, use card types for an alternative feature. In fact, the indicators studied on this basis are defined as meeting or not meeting the requirements. Hence the use of maps for the proportion (number) of defects and the number of conformances (inconsistencies) per unit of production.
For any type of Shewhart maps, the definition of the central and control lines, where the central line (CL-controllimit) actually represents the average value of the indicator, and the control limits (UCL-uppercontrollimit; LCL-lowercontrollimit) are the allowable tolerance values.
The values of the upper and lower control limits are determined by the formulas for different types charts, as can be seen from the diagram in Appendix 1. To calculate them, in order to replace cumbersome formulas, coefficients from special tables are used to build control charts, where the value of the coefficient depends on the sample size (Appendix 2). If the sample size is large, then maps are used that provide the most complete information.
At this stage, the researcher must calculate the values of CL, UCL, LCL.
V. Construction of a control chart.
So, we have come to the most interesting process - a graphical representation of the data obtained. So, if the data was entered into a computer, then using the Statistica or Excel program environment, you can quickly graphically display the data. However, it is possible to build a control chart and, without special programs, then, along the OY axis of the control charts, we plot the values of the quality indicator, and along the OX axis, the time points of registering the values, in the following sequence:
1. plot the center line (CL) on the control chart
2. draw borders (UCL; LCL)
3. We reflect the data obtained during the study by applying an appropriate marker to the point of intersection of the value of the indicator and the time of its registration. It is recommended to use different types of markers for values that are inside and outside the tolerance limits.
4. In case of using double cards, repeat steps 1-3 for the second card.
VI. Checking the stability and controllability of the process.
This stage is designed to show us what the research was conducted for - whether the process is stable. Stability (statistical controllability) is understood as a state in which the repeatability of parameters is guaranteed. Thus, the process will be stable only if the following cases do not occur.
Consider the main criteria for process instability:
1. Going beyond the control limits
2. A series is a certain number of points, which invariably turns out to be on one side of the center line - (top) bottom.

A series of seven points is considered abnormal. In addition, the situation should be considered abnormal if:
a) at least 10 out of 11 points are on the same side of the center line;
b) at least 12 out of 14 points are on the same side of the center line;
c) at least 16 out of 20 points are on the same side of the center line.
3. trend - a continuously rising or falling curve.

4. approaching the control limits. If 2 or 3 points are very close to the control limits, this indicates an abnormal distribution.

5. approaching the center line. If the values are concentrated near the center line, this may indicate an incorrect choice of grouping method, which makes the range too wide and leads to data mixing with different distributions.

6. periodicity. When, after certain equal intervals of time, the curve goes either to "decline", or to "rise".

VII. Analysis of control charts.
Further actions are based on the conclusion about the stability or instability of the process. If the process does not meet the stability criteria, the influence of non-random factors should be reduced and, by collecting new data, a control chart should be built. But, if the process meets the stability criteria, it is necessary to evaluate the process capabilities (Cp). The smaller the spread of parameters within the tolerance limits, the higher the value of the process capability indicator. The indicator reflects the ratio of the width of the parameter and the degree of its dispersion. Opportunity index is calculated as ![]() , where can be calculated as .
, where can be calculated as .
If the calculated index is less than 1, then the researcher needs to improve the process, either stop the production of the product, or change the requirements for the product. With index value:
Wed<1 возможности процесса неприемлемы,
Cр=1 the process is on the verge of the required capabilities,
Cp>1 the process satisfies the criterion of possibility.
If there is no displacement relative to the central line Cp=Cpk, where ![]() . These two indicators are always used together to determine the status of the process, for example, in mechanical engineering it is considered the norm
. These two indicators are always used together to determine the status of the process, for example, in mechanical engineering it is considered the norm ![]() , which means that the probability of non-compliance does not exceed 0.00006.
, which means that the probability of non-compliance does not exceed 0.00006.
Now, having considered the algorithm for constructing control charts, we will analyze a specific example.
Task: Chromium content in steel castings is controlled. Measurements are carried out in four swimming trunks. Table 2 shows data for 15 subgroups. You need to build a map.
Solution: Since it is already known in advance what type of map needs to be built, we calculate the values
| subgroup number | X1 | X2 | X3 | X4 | R | |
| 1 | 0,74 | 0,76 | 0,62 | 0,73 | 0,713 | 0,14 |
| 2 | 0,72 | 0,74 | 0,84 | 0,69 | 0,748 | 0,15 |
| 3 | 0,87 | 0,79 | 0,70 | 0,92 | 0,820 | 0,22 |
| 4 | 0,78 | 0,66 | 0,71 | 0,74 | 0,723 | 0,12 |
| 5 | 0,81 | 0,66 | 0,82 | 0,67 | 0,740 | 0,16 |
| 6 | 0,63 | 0,71 | 0,68 | 0,82 | 0,710 | 0,19 |
| 7 | 0,63 | 0,73 | 0,64 | 0,80 | 0,700 | 0,17 |
| 8 | 0,66 | 0,68 | 0,85 | 0,91 | 0,775 | 0,25 |
| 9 | 0,63 | 0,66 | 0,62 | 0,85 | 0,690 | 0,23 |
| 10 | 0,85 | 0,61 | 0,75 | 0,77 | 0,745 | 0,24 |
| 11 | 0,73 | 0,65 | 0,74 | 0,90 | 0,755 | 0,25 |
| 12 | 0,85 | 0,77 | 0,65 | 0,69 | 0,740 | 0,20 |
| 13 | 0,67 | 0,69 | 0,83 | 0,62 | 0,703 | 0,21 |
| 14 | 0,74 | 0,73 | 0,62 | 0,88 | 0,743 | 0,26 |
| 15 | 0,81 | 0,82 | 0,69 | 0,73 | 0,763 | 0,13 |
| medium: | 0,738 | 0,19 |
The next step is to calculate , where, according to the above scheme, , and ![]() . Now, having the values of the central line, the average value of the indicator and the average deviation, we will find the values of the control borders of the maps.
. Now, having the values of the central line, the average value of the indicator and the average deviation, we will find the values of the control borders of the maps.
![]()
![]() , where is according to the table of coefficients for calculating the lines of control charts and is equal to 0.729. Then UCL=0.880 , LCL=0.596.
, where is according to the table of coefficients for calculating the lines of control charts and is equal to 0.729. Then UCL=0.880 , LCL=0.596.
For values, the lower and upper control limits are determined by the formulas:
where and are found according to the table of coefficients for calculating the lines of control charts and are equal to 0.000 and 2.282, respectively. Then UCL=0.19*2.282=0.444 and LCL=0.19*0.000=0.
Let's build control charts for the averages and ranges of this sample using Excel:


As we can verify, the control charts did not reveal non-random values, out-of-control limits, series or trends. However, the graph of average values tends to the central position, which may indicate both incorrectly chosen tolerance limits, and the abnormality of the distribution and instability of the process. To make sure, we calculate the process capability index. ![]() , where can be calculated as , according to the table of coefficients, we find the value equal to ;
, where can be calculated as , according to the table of coefficients, we find the value equal to ;

Since, the computed index<1, что свидетельствует о неприемлемости возможностей процесса, его статистической неуправляемости и не стабильности. Необходимо провести усовершенствования процесса, установить контроль над его протеканием, с целью уменьшения влияния не случайных факторов.
Studying specialized literature and delving into quality management, I was able to gather a large amount of interesting and useful information. For example, the breadth of the use of quality management has affected all areas of production from heavy industry and oil procurement to small organizations providing services (catering places, bookstores, etc.).
In recent years, under the overarching influence of thinking aimed at improving quality and customer satisfaction, systems such as CRM-customer-oriented management are attributed to quality management; ERP enterprise resource management system; TPM - system of general care of the equipment, and many other systems. Based on this, we can conclude that there has been a shift in interests from quality management of a specific process to the use of quality systems and software packages that allow one way or another to contribute to customer satisfaction in the most convenient ways. The contribution of Walter Shewhart to statistical quality management is great, and the control charts he proposed are still used, but more often, in conjunction with other methods, due to the provision of a systematic approach and the consideration of many factors that were not taken into account back in the 20th century.
In conclusion, I would like to say that the main problem of modern quality systems is that, with all the apparent ease of use, they cannot guarantee their effective use in the enterprise. The reasons lie in the origins! After all, the main advantage of using the "7 Simple Methods" of quality management is that without the penetration of the quality philosophy, it is hardly possible to obtain any significant results. Thus, companies that are not yet ready for fundamental changes could save themselves from the introduction of expensive systems and unnecessary spending.
Quality management is the philosophy of success for modern companies!
1. GOST R 50779.42-99 " Statistical Methods. Shewhart's Control Charts"
2. Goldrat E.M., Cox J. Purpose. The process of continuous improvement / E.M. Goldrat, J. Cox. - Potpourri Publishing House -2007.
3. Yosio Kondo. Quality management across the company: formation and stages of development. / Per. from English. E.P. Markova, I.N. Rybakov. - Nizhny Novgorod: SMC "priority", 2002.
4. Prosvetov G.I. Forecasting and planning: tasks and solutions: teaching aid./G.I. Prosveov-M.: RDL Publishing House, 2005.
5. Kane M.M., Ivanov B.V., Koreshkov V.N., Skhirtladze A.G. Systems, methods and tools of quality management / M.M. Canet, B.V. Ivanov, V.N. Koreshkov, A.G. Skhirtladze. - St. Petersburg: Peter, 2009
6. Kachalov V.A. What is “continuous improvement of the effectiveness of the QMS”?// Methods of quality management.-2006.-№10.
7. Klyachkin V.N. Statistical methods in quality management: computer technology: textbook. Allowance / V.N. Klyachkin.-M.: Finance and statistics, 2007.
8. Kruglov M.G., Shishkov G.M. Quality management as it is / M.G. Kruglov, G.M. Shishkov.-M.: Eksmo, 2006.
9. Kuznetsov L.A. Control and evaluation of multidimensional quality//Methods of quality management.-2008.-№10.-p. 40-45.
10. Sazhin Yu.V., Pletneva N.P. On the question of the effectiveness of QMS in Russia// Methods of quality management.-2008.-№10.-P.20-24.
11. Statistical methods of quality improvement: monograph / trans. from English. Yu.P.Adler, L.A. Konareva; ed. Kume.-M.: Finance and statistics, 1990.
12. Feigenbaum A. Product quality control / A. Feigenbaum. - M.: Economics, 1986.
13. Evans J. Quality management: textbook. Allowance/J. Evans.-M.: Unity-Dana, 2007.
Shewhart's chart of control charts

Coefficients for calculating lines of control charts.

Kane M.M., Ivanov B.V., Koreshkov V.N., Skhirtladze A.G. Systems, methods and tools of quality management / M.M. Canet, B.V. Ivanov, V.N. Koreshkov, A.G. Skhirtladze. - St. Petersburg: Peter, 2009
Kane M.M., Ivanov B.V., Koreshkov V.N., Skhirtladze A.G. Systems, methods and tools of quality management / M.M. Canet, B.V. Ivanov, V.N. Koreshkov, A.G. Skhirtladze. - St. Petersburg: Peter, 2009.
Federal Agency for Education
State educational institution
higher professional education
"Kuzbass State Technical University"
Department of Plastics Processing Technology
Department of Chemical Technology of Inorganic Substances
Shewhart Control Charts
Methodological instructions for practical exercises in the discipline
"Metrology, standardization, certification"
for students of specialties
250100 (240401) "Chemical technology of organic substances"
250200 (240301) "Chemical technology of inorganic substances"
250400 (240403) "Chemical technology of natural energy carriers
and carbon materials"
250600(240502) "Technology for processing plastics and elastomers"
Compiled by N. M. Igolinskaya
E. B. Silinina
M. A. Igolinskaya
Approved at the meeting of the department
educational and methodological commission
specialties 250200
Minutes No. 8 dated 30.03.2006
The electronic copy is
in the library of the main building
GU KuzGTU
Kemerovo 2006
OBJECTIVES OF PRACTICAL EXERCISES
Familiarize yourself with the methods of constructing Shewhart control charts; according to the assignment option, calculate the boundaries and build a map to control the process.
Make a conclusion about the process and its statistical controllability.
Perform procedures for bringing the map to the form of a statistically controlled process.
1. MAIN PROPOSITIONS OF THE THEORY
SHUKHART CONTROL CHARTS
Control charts are graphical tools that use statistical approaches to control production processes. The purpose of such a control is to determine whether a statistically controlled state of the process has been reached and whether it remains in this state with continuous information about the quality of the product.
Controlling the stability of the process allows you to reduce the cost of quality control of the finished product, choose the right raw material base and the price of products as a commodity.
Control chart theory distinguishes between two types of variability:
- variability due to random causes that are constantly present and cannot be identified and eliminated;
- variability, which is real changes in the process due to certain reasons that can be identified and eliminated. Such variability is considered as “non-random” (tool breakage, heterogeneity of raw materials, violation of the technological regime, personnel qualification, etc.).
Variability due to random causes is usually described by the parameters of a normal distribution and a Gaussian curve, which must be within the process tolerance band. This position is shown in Fig. one.
The ratio of the boundaries shown in the figure makes it possible to establish, in relation to the areas of the ranges σ, the relationship between the hit frequency X 0 into and out of range. These frequencies are given in Table. one.
Rice. 1. The ratio of distribution boundaries (B) and technological tolerance (T) for an established statistically controlled process
Table 1
Relationship between the specified parameter deviation range X
and frequency of hits and misses X in this range
|
Target range parameter deviation X |
Hit frequency parameter X in the range, % |
Parameter hit frequency X out of range, % |
|
|
| |
|
| ||
|
| ||
|
|
Therefore, if the requirements for the process are determined in such a way that the spread of control parameters does not exceed  , then the output of any, taken at random, given control parameter X i out of range
, then the output of any, taken at random, given control parameter X i out of range  possible with a probability of 0.06, i.e. unlikely.
possible with a probability of 0.06, i.e. unlikely.
We introduce the characteristic I B - "process capability index". This value determines the possibilities of the process and its statistical regulation. It is determined by the formula
 ,
(1)
,
(1)
where I B is the process capability index;
T– requirement for the process;
AT– process capabilities.
If a I B< 1, то процесс невозможен (не может быть обеспечено требуемое качество).
If a I B = 1, then the process is on the verge of the possible. At the same time, despite the fact that the process under favorable conditions can provide a given quality, its statistical regulation is impossible.
If a I B > 1, then the process is possible and statistical regulation of its quality can be implemented.
A general view of one of the possible control charts is shown in fig. 2.

Rice. 2. Control chart of the distribution of the current values of the controlled parameter X by 18 measurement groups
Statistical quality control of the process is clearly shown in fig. 3 .

Rice. 3. Schematic representation of a statistically controlled process
I recently posted mine here, where enough plain language, in places abusing foul language, under a 20-minute laughter of listeners, he talked about how to separate systemic variations from variations caused by special reasons.
Now I want to analyze in detail an example of constructing a Shewhart control chart based on real data. As real data, I took historical information about completed personal tasks. I have this information thanks to the adaptation of David Allen's personal effectiveness model Getting Things (I also have an old slidecast about this in three parts: Part 1, Part 2, Part 3 + Excel table with macros for analyzing tasks from Outlook).
The task statement looks like this. I have a distribution of the average number of completed tasks depending on the day of the week (below in the graph) and I need to answer the question: “is there anything special about Mondays or is it just a system error?”
Let's answer this question with the help of the Shewhart control chart, the main tool of statistical process control.
So, Shewhart's criterion for the presence of a special cause of variation is quite simple: if some point goes beyond the control limits, calculated in a special way, then it indicates a special cause. If the point lies within these limits, then the deviation is due to the general properties of the system itself. Roughly speaking, is the measurement error.
The formula for calculating the control limits looks like this:
Where
- the average value of the average values for the subgroup,
- average range,
- some engineering coefficient depending on the size of the subgroup.
All formulas and tabular coefficients can be found, for example, in GOST 50779.42-99, where the approach to statistical management is briefly and clearly stated (honestly, I myself did not expect that there is such a GOST. The topic of statistical management and its place in business optimization is disclosed in more detail in book by D. Wheeler).
In our case, we group the number of completed tasks by day of the week - these will be the subgroups of our sample. I took data on the number of completed tasks for 5 weeks of work, that is, the size of the subgroup is 5. Using table 2 from GOST, we find the value of the engineering coefficient:
Calculating the average value and range (the difference between the minimum and maximum values) for a subgroup (in our case, by the day of the week) is a fairly simple task, in my case the results are as follows:
The central line of the control chart will be the mean of the group means, i.e.:
We also calculate the average range:
Now we know that the lower control limit for the number of completed tasks will be equal to:
That is, those days on which I complete fewer tasks on average are special from the point of view of the system.
Similarly, we obtain the upper control limit:
Now plot the center line (red), upper control limit (green), and lower control limit (purple) on the chart:

And, oh, miracle! We see three clearly distinct groups outside the control limits, in which there are clearly not systemic causes variations!
I don't work on Saturdays and Sundays. Fact. And Monday was a really special day. And now you can think and look for what is really special on Mondays.
However, if the average number of tasks completed on Monday were within the control limits and even if it stood out strongly against the background of other points, then from the point of view of Shewhart and Deming, it would be pointless to look for any features on Mondays, since such behavior is determined solely by general causes. . For example, I built a control chart for another 5 weeks at the end of last year:

And it seems like there is some kind of feeling that Monday somehow stands out, but according to the Shewhart criterion, this is just a fluctuation or an error in the system itself. According to Shewhart, this case you can explore the special causes of Mondays for an arbitrarily long time - they simply do not exist. From the point of view of the statistical office, on these data, Monday is no different from any other working day (even Sundays).

 68,26
68,26