TEXTO EXPLICACIÓN DE LA LECCIÓN:
La idea de un plano en el espacio te permite obtener, por ejemplo, la superficie de una mesa o una pared. Sin embargo, una mesa o una pared tiene dimensiones finitas y el plano se extiende más allá de sus límites hasta el infinito.
Considere dos planos que se intersecan. Cuando se cortan, forman cuatro ángulos diédricos con una arista común.
Recordemos qué es un ángulo diedro.
En realidad, nos encontramos con objetos que tienen la forma de un ángulo diedro: por ejemplo, una puerta entreabierta o una carpeta entreabierta.
En la intersección de dos planos alfa y beta, obtenemos cuatro ángulos diédricos. Sea uno de los ángulos diedros igual a (phi), luego el segundo es igual a (1800-), el tercero, el cuarto (1800-).
Considere el caso cuando uno de los ángulos diedros es igual a 900.
Entonces, todos los ángulos diedros en este caso son iguales a 900.
Introduzcamos la definición de planos perpendiculares:
Se dice que dos planos son perpendiculares si el ángulo diedro entre ellos es de 90°.
El ángulo entre los planos sigma y epsilon es de 90 grados, lo que significa que los planos son perpendiculares.
Pongamos ejemplos de planos perpendiculares.
Pared y techo.

Pared lateral y tablero de mesa.
Formulemos un signo de perpendicularidad de dos planos:
TEOREMA: Si uno de dos planos pasa por una recta perpendicular al otro plano, entonces estos planos son perpendiculares.
Probemos esta característica.
Por condición, se sabe que la línea AM está en el plano α, la línea AM es perpendicular al plano β,
Demostrar: los planos α y β son perpendiculares.
Prueba:
1) Los planos α y β se cortan a lo largo de la línea recta АР, mientras que AM АР, ya que AM β por la condición, es decir, AM es perpendicular a cualquier línea que se encuentre en el plano β.
2) Dibujemos una línea AT perpendicular a AP en el plano β.
Obtenemos el ángulo TAM, el ángulo lineal del ángulo diedro. Pero el ángulo TAM = 90°, ya que MA β. Por lo tanto, α β.

QED
Del signo de la perpendicularidad de dos planos, tenemos una consecuencia importante:
CONSECUENCIA: Un plano perpendicular a una recta por la que se cortan dos planos es perpendicular a cada uno de estos planos.
Es decir: si α∩β=с y γ с, entonces γ α y γ β.
Probemos este corolario: si el plano gamma es perpendicular a la recta c, entonces, debido al paralelismo de los dos planos, gamma es perpendicular a alfa. De manera similar, gamma es perpendicular a beta.
Reformulemos este corolario para un ángulo diedro:
El plano que pasa por el ángulo lineal del ángulo diedro es perpendicular a la arista y las caras de este ángulo diedro. En otras palabras, si hemos construido un ángulo lineal de un ángulo diedro, entonces el plano que lo atraviesa es perpendicular a la arista y caras de este ángulo diedro.
Dado: ΔABC, C = 90°, AC se encuentra en el plano α, ángulo entre los planos α y ABC = 60°, AC = 5 cm, AB = 13 cm.
Hallar: distancia del punto B al plano α.

1) Construyamos la CV α. Entonces el CS es la proyección del BC sobre este plano.
2) BC AS (por condición), por lo tanto, por el teorema de las tres perpendiculares (TTP), CS AS. Por lo tanto, VSK es el ángulo lineal del ángulo diedro entre el plano α y el plano del triángulo ABC. Es decir, WSC = 60°.
3) De ΔBCA según el teorema de Pitágoras:
Respuesta VK es igual a 6 raíces de tres cm
Uso práctico (carácter aplicado) de la perpendicularidad de dos planos.
Dos rectas en el espacio se llaman perpendiculares si el ángulo entre ellas es de 90°.
arroz. 37 |
Las líneas perpendiculares pueden intersecarse y pueden estar sesgadas. Lema. Si una de dos líneas paralelas es perpendicular a una tercera línea, entonces la otra línea también es perpendicular a esta línea. Definición. Se dice que una línea es perpendicular a un plano si es perpendicular a cualquier línea que se encuentre en el plano. También decimos que el plano es perpendicular a la línea a. |
arroz. 38 |
Si la línea a es perpendicular al plano, obviamente lo corta. De hecho, si la línea a no intersecara al plano, estaría en este plano o sería paralela a él. Pero en ambos casos habría líneas en el plano no perpendiculares a la línea a, por ejemplo, líneas paralelas a ella, lo cual es imposible. Entonces la recta a corta al plano. |
Relación entre rectas paralelas y su perpendicularidad al plano.
Un signo de perpendicularidad de una línea recta y un plano.
Comentarios.
- Por cualquier punto del espacio pasa un plano perpendicular a una línea dada, y además, el único.
- Por cualquier punto del espacio pasa una recta perpendicular a un plano dado, y además una sola.
- Si dos planos son perpendiculares a una recta, entonces son paralelos.
Tareas y pruebas sobre el tema "Tema 5. "Perpendicularidad de una línea recta y un plano".
- Perpendicularidad de una recta y un plano
- Ángulo diedro. perpendicularidad del plano - Perpendicularidad de rectas y planos clase 10
Lecciones: 1 Tareas: 10 Pruebas: 1
- Perpendiculares y oblicuas. Ángulo entre recta y plano - Perpendicularidad de rectas y planos clase 10
Lecciones: 2 Tareas: 10 Pruebas: 1
- Paralelismo de rectas, recta y plano - Paralelismo de rectas y planos grado 10
Lecciones: 1 Tareas: 9 Pruebas: 1
- Lineas perpendiculares - Información geométrica básica Grado 7
Lecciones: 1 Tareas: 17 Pruebas: 1
El material del tema resume y sistematiza la información sobre la perpendicularidad de las líneas que conoce de la planimetría. Es recomendable combinar el estudio de los teoremas sobre la relación entre el paralelismo y la perpendicularidad de las líneas y los planos en el espacio, así como el material sobre la perpendicular y la oblicua, con una repetición sistemática del material relevante de la planimetría.
Las soluciones de casi todos los problemas computacionales se reducen a la aplicación del teorema de Pitágoras y sus consecuencias. En muchos problemas, la posibilidad de aplicar el teorema de Pitágoras o sus consecuencias se justifica por el teorema de las tres perpendiculares o por las propiedades de paralelismo y perpendicularidad de los planos.
El concepto de planos perpendiculares.
Cuando dos planos se intersecan, obtenemos $4$ ángulos diédricos. Dos de las esquinas son $\varphi $ y las otras dos son $(180)^0-\varphi $.
Definición 1
El ángulo entre los planos es el menor de los ángulos diédricos formados por estos planos.
Definición 2
Dos planos que se cortan se llaman perpendiculares si el ángulo entre estos planos es igual a $90^\circ$ (Fig. 1).
Figura 1. Planos perpendiculares
Signo de perpendicularidad de dos planos.
Teorema 1
Si una línea de un plano es perpendicular a otro plano, entonces estos planos son perpendiculares entre sí.
Prueba.
Sean dados los planos $\alpha $ y $\beta $ que se cortan a lo largo de la recta $AC$. Sea la línea $AB$ que está en el plano $\alpha $ perpendicular al plano $\beta $ (Fig. 2).

Figura 2.
Dado que la línea $AB$ es perpendicular al plano $\beta $, también es perpendicular a la línea $AC$. Dibujemos adicionalmente la línea $AD$ en el plano $\beta $, perpendicular a la línea $AC$.
Obtenemos que el ángulo $MALO$ es el ángulo lineal del ángulo diédrico igual a $90^\circ$. Es decir, por definición 1, el ángulo entre los planos es igual a $90^\circ$, lo que significa que estos planos son perpendiculares.
El teorema ha sido probado.
El siguiente teorema se deriva de este teorema.
Teorema 2
Si un plano es perpendicular a una línea a lo largo de la cual se cortan otros dos planos, entonces también es perpendicular a estos planos.
Prueba.
Sean dados dos planos $\alpha $ y $\beta $ que se cortan a lo largo de la recta $c$. El plano $\gamma $ es perpendicular a la recta $c$ (Fig. 3)

figura 3
Como la línea $c$ pertenece al plano $\alpha $ y el plano $\gamma $ es perpendicular a la línea $c$, entonces, por el Teorema 1, los planos $\alpha $ y $\gamma $ son perpendiculares.
Como la recta $c$ pertenece al plano $\beta $ y el plano $\gamma $ es perpendicular a la recta $c$, entonces, por el Teorema 1, los planos $\beta $ y $\gamma $ son perpendiculares.
El teorema ha sido probado.
Para cada uno de estos teoremas, las afirmaciones inversas también son verdaderas.
Ejemplos de tareas
Ejemplo 1
Tengamos una caja rectangular $ABCDA_1B_1C_1D_1$. Encuentre todos los pares de planos perpendiculares (Fig. 5).
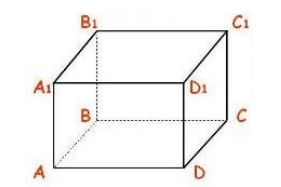
Figura 4
Decisión.
Por definición de un paralelepípedo y planos perpendiculares, vemos los siguientes ocho pares de planos perpendiculares entre sí: $(ABB_1)$ y $(ADD_1)$, $(ABB_1)$ y $(A_1B_1C_1)$, $(ABB_1) $ y $(BCC_1) $, $(ABB_1)$ y $(ABC)$, $(DCC_1)$ y $(ADD_1)$, $(DCC_1)$ y $(A_1B_1C_1)$, $(DCC_1)$ y $(BCC_1)$, $(DCC_1)$ y $(ABC)$.
Ejemplo 2
Sean dados dos planos mutuamente perpendiculares. Desde un punto de un plano se traza una perpendicular a otro plano. Demostrar que esta línea se encuentra en el plano dado.
Prueba.
Seamos $\alpha $ y $\beta $ perpendiculares a los planos y que se cortan a lo largo de la recta $c$. Desde el punto $A$ del plano $\beta $ se traza una perpendicular $AC$ al plano $\alpha $. Suponga que $AC$ no se encuentra en el plano $\beta $ (Fig. 6).
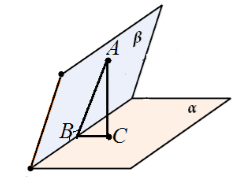
Figura 5
Considere el triángulo $ABC$. Es rectangular con ángulo recto $ACB$. Por lo tanto, $\ángulo ABC\ne (90)^0$.
Pero, por otro lado, $\angle ABC$ es el ángulo lineal del ángulo diedro formado por estos planos. Es decir, el ángulo diedro formado por estos planos no es igual a 90 grados. Obtenemos que el ángulo entre los planos no es igual a $90^\circ$. Contradicción. Por lo tanto, $AC$ se encuentra en el plano $\beta $.
Esta lección ayudará a aquellos que deseen tener una idea sobre el tema "Un signo de perpendicularidad de dos planos". Al comienzo del mismo, repetiremos la definición de diedro y ángulo lineal. Luego consideraremos qué planos se llaman perpendiculares y probaremos el criterio para la perpendicularidad de dos planos.
Tema: Perpendicularidad de rectas y planos
Lección: Signo de perpendicularidad de dos planos
Definición. Un ángulo diedro es una figura formada por dos semiplanos que no pertenecen al mismo plano, y su recta común a (a es una arista).
Arroz. uno
Considere dos semiplanos α y β (Fig. 1). Su borde común es l. Esta figura se llama ángulo diedro. Dos planos que se cortan forman cuatro ángulos diédricos con una arista común.
Un ángulo diedro se mide por su ángulo lineal. Elegimos un punto arbitrario en una arista común l del ángulo diedro. En los semiplanos α y β desde este punto trazamos las perpendiculares a y b a la recta l y obtenemos el ángulo lineal del ángulo diedro.
Las líneas rectas a y b forman cuatro ángulos iguales a φ, 180° - φ, φ, 180° - φ. Recuerda que el menor de estos ángulos se llama ángulo entre rectas.
Definición. El ángulo entre los planos es el menor de los ángulos diédricos formados por estos planos. φ - ángulo entre los planos α y β, si
Definición. Dos planos que se cortan se llaman perpendiculares (mutuamente perpendiculares) si el ángulo entre ellos es de 90°.

Arroz. 2
Se elige un punto M arbitrario en el borde l (Fig. 2). Dibujemos dos rectas perpendiculares MA = a y MB = b a la arista l en el plano α y en el plano β, respectivamente. Tenemos el ángulo AMB. El ángulo AMB es el ángulo lineal de un ángulo diédrico. Si el ángulo AMB es de 90°, se dice que los planos α y β son perpendiculares.
La línea b es perpendicular a la línea l por construcción. La línea b es perpendicular a la línea a, ya que el ángulo entre los planos α y β es de 90°. Obtenemos que la recta b es perpendicular a dos rectas ayl que se cortan desde el plano α. Por lo tanto, la línea b es perpendicular al plano α.
De manera similar, se puede probar que la línea a es perpendicular al plano β. La línea a es perpendicular a la línea l por construcción. La línea a es perpendicular a la línea b, ya que el ángulo entre los planos α y β es de 90°. Obtenemos que la recta a es perpendicular a dos rectas b y l que se cortan desde el plano β. Por lo tanto, la línea a es perpendicular al plano β.
Si uno de dos planos pasa por una línea perpendicular al otro plano, entonces dichos planos son perpendiculares.
Demostrar:

Arroz. 3
Prueba:
Deje que los planos α y β se corten a lo largo de la línea recta AC (Fig. 3). Para demostrar que los planos son mutuamente perpendiculares, debe construir un ángulo lineal entre ellos y demostrar que este ángulo es igual a 90 °.
La línea AB es perpendicular por la condición al plano β y, por lo tanto, también a la línea AC que se encuentra en el plano β.
Dibujemos la línea AD perpendicular a la línea AC en el plano β. Entonces BAD es el ángulo lineal del ángulo diedro.
La línea AB es perpendicular al plano β y, por lo tanto, también a la línea AD que se encuentra en el plano β. Entonces el ángulo lineal BAD es de 90°. Por lo tanto, los planos α y β son perpendiculares, lo cual debía probarse.
El plano perpendicular a la línea a lo largo de la cual se cortan dos planos dados es perpendicular a cada uno de estos planos (Fig. 4).
Demostrar:

Arroz. 4
Prueba:
La recta l es perpendicular al plano γ, y el plano α pasa por la recta l. Por tanto, por el criterio de la perpendicularidad de los planos, los planos α y γ son perpendiculares.
La recta l es perpendicular al plano γ, y el plano β pasa por la recta l. Por lo tanto, por el signo de la perpendicularidad de los planos, los planos β y γ son perpendiculares.
Conferencia sobre el tema "Un signo de perpendicularidad de dos planos"
La idea de un plano en el espacio te permite obtener, por ejemplo, la superficie de una mesa o una pared. Sin embargo, una mesa o una pared tiene dimensiones finitas y el plano se extiende más allá de sus límites hasta el infinito.Considere dos planos que se intersecan. Cuando se cortan, forman cuatro ángulos diédricos con una arista común.
Recordemos qué es un ángulo diedro.
En realidad, nos encontramos con objetos que tienen la forma de un ángulo diedro: por ejemplo, una puerta entreabierta o una carpeta entreabierta.

En la intersección de dos planos alfa y beta, obtenemos cuatro ángulos diédricos. Sea uno de los ángulos diedros igual a (phi), entonces el segundo es igual a (180 0 -), tercero, cuarto (180 0 -).

α yβ, 0°< 90 °
Considere el caso cuando uno de los ángulos diédricos es igual a 90 0 .
Entonces, todos los ángulos diedros en este caso son iguales a 90 0 .
ángulo diedro entre planosα yβ,
90º
Introduzcamos la definición de planos perpendiculares:
Se dice que dos planos son perpendiculares si el ángulo diedro entre ellos es de 90°.
El ángulo entre los planos sigma y epsilon es de 90 grados, lo que significa que los planos son perpendiculares.
Porque =90°
Pongamos ejemplos de planos perpendiculares.
Pared y techo.
Pared lateral y tablero de mesa.

pared y techo
Formulemos un signo de perpendicularidad de dos planos:
TEOREMA:Si uno de dos planos pasa por una línea perpendicular al otro plano, entonces estos planos son perpendiculares.
Probemos esta característica.
Por suposición, se sabe que la líneaAM se encuentra en el plano α, la línea AM es perpendicular al plano β,
Demostrar: los planos α y β son perpendiculares.
Prueba:
1) Planos α yβ se cruzan a lo largo de la línea AR, mientras que AM AR, ya que AM β por la condición, es decir, AM es perpendicular a cualquier línea que se encuentre en el plano β.
2) Dibujar una línea recta en el plano βUNT perpendicularUNr
Obtenemos el ángulo TUNM es el ángulo lineal del ángulo diedro. Pero el ángulo TUNM = 90°, ya que MA β. Por lo tanto, α β.
QED
TEOREMA:Si un plano pasa por una recta perpendicular a otro plano, entonces estos planos son perpendiculares.

Dado:α, β, AM α, AMβ, AM∩=A
Demostrar: αβ.
Prueba:
1) α∩β = АР, mientras que AM АР, ya que AM β por la condición, es decir, AM es perpendicular a cualquier línea que se encuentre en el plano β.
2) ATβ,UNTUNr
TAM es el ángulo lineal de un ángulo diedro. TAM = 90°, porque MA β. Por lo tanto, α β.
QED
Del signo de la perpendicularidad de dos planos, tenemos una consecuencia importante:
CONSECUENCIA:Un plano perpendicular a una línea a lo largo de la cual se cortan dos planos es perpendicular a cada uno de estos planos.
Probemos este corolario: si el plano gamma es perpendicular a la recta c, entonces, debido al paralelismo de los dos planos, gamma es perpendicular a alfa. De manera similar, gamma es perpendicular a beta.

Es decir: si α∩β=с y γс, entonces γα y γβ.
porqueγс y сα del signo de perpendicularidad γα.
Del mismo modo, γ β
Reformulemos este corolario para un ángulo diedro:
El plano que pasa por el ángulo lineal del ángulo diedro es perpendicular a la arista y las caras de este ángulo diedro. En otras palabras, si hemos construido un ángulo lineal de un ángulo diedro, entonces el plano que lo atraviesa es perpendicular a la arista y caras de este ángulo diedro.

Tarea.
Dado: ΔABC, C = 90°, AC se encuentra en el plano α, el ángulo entre los planos α yA B C= 60°, CA = 5 cm, AB = 13 cm.
Hallar: distancia del punto B al plano α.
Decisión:
1) Construyamos la CV α. Entonces el CS es la proyección del BC sobre este plano.
2) BC AS (por condición), por lo tanto, por el teorema de las tres perpendiculares (TTP), CS AS. Por lo tanto, VSK es el ángulo lineal del ángulo diedro entre el plano α y el plano del triángulo ABC. Es decir, WSC = 60°.
3) De ΔBCA según el teorema de Pitágoras:
De ΔVKS: ![]()


















