Primjeri dijeljenja decimala cijelim brojem. Sastavljanje sustava jednadžbi

Zbrajanje decimala vrši se na isti način kao i zbrajanje cijelih brojeva. Pogledajmo to na primjerima.

1) 0,132 + 2,354. Potpišimo uvjete jedan pod drugim.

Ovdje se od zbrajanja 2 tisućinke s 4 tisućinke dobilo 6 tisućinki;
od zbrajanja 3 stotinke s 5 stotinki, ispalo je 8 stotinki;
od zbrajanja 1 desetinke sa 3 desetinke -4 desetinke i
od zbrajanja 0 cijelih brojeva s 2 cijela broja - 2 cijela broja.

2) 5,065 + 7,83.

U drugom mandatu nema tisućinki pa je važno ne pogriješiti pri potpisivanju uvjeta jedan pod drugim.

3) 1,2357 + 0,469 + 2,08 + 3,90701.

Ovdje pri zbrajanju tisućinki dobivamo 21 tisućinku; pod tisućinke smo napisali 1, a stotinkama dodali 2, pa smo na stotom mjestu dobili sljedeće pojmove: 2 + 3 + 6 + 8 + 0; u zbroju daju 19 stotinki, mi smo potpisali 9 pod stotinke, a 1 se računala kao desetinke itd.

Dakle, kada se zbrajaju decimalni razlomci, mora se promatrati sljedeća narudžba: znak razlomaka jedan ispod drugog tako da u svim pojmovima iste znamenke budu jedna ispod druge i svi zarezi budu u istom okomitom stupcu; desno od decimalnih mjesta nekih pojmova pripisuju, barem mentalno, toliki broj nula tako da svi članovi nakon decimalne točke imaju isti broj znamenke. Zatim se zbrajanje vrši po znamenkama, počevši s desne strane, a u dobivenom zbroju stavljaju zarez u isti okomiti stupac kao što je to u ovim pojmovima.

§ 108. Oduzimanje decimalnih razlomaka.

Oduzimanje decimala vrši se na isti način kao i oduzimanje cijelih brojeva. Pokažimo to primjerima.

1) 9,87 - 7,32. Potpišimo oduzetak ispod minusa tako da jedinice iste znamenke budu jedna ispod druge:

2) 16.29 - 4.75. Potpišimo oduzetak ispod minusa, kao u prvom primjeru:

Da bi se oduzele desetine, trebalo je uzeti jednu cijelu jedinicu od 6 i podijeliti je na desetine.

3) 14.0213-5.350712. Potpišimo oduzetak ispod minusa:

Oduzimanje je izvedeno na sljedeći način: budući da od 0 ne možemo oduzeti 2 milijuntinke, trebali bismo se odnositi na najbližu znamenku s lijeve strane, tj. na stotisuću, ali postoji i nula umjesto stotisućinki, pa uzimamo 1 desettisućinka od 3 desettisućinke i podijelimo je na stotisućinke, dobijemo 10 stotisućinki, od čega je 9 stotisućinki ostalo u kategoriji stotisućinki, a 1 stotisućinku dijelimo na milijuntinke, dobivamo 10 milijuna. Dakle, u zadnja tri znamenke koje smo dobili: milijuntinke 10, stotisućinke 9, desettisućinke 2. Radi veće jasnoće i praktičnosti (da ne zaboravimo), ovi su brojevi napisani na vrhu odgovarajućih razlomaka reduciranog broja. Sada možemo početi oduzimati. Od 10 milijuna oduzmemo 2 milijuntinke, dobijemo 8 milijuna; oduzmemo 1 stotisućinku od 9 stotisućinki, dobijemo 8 stotisućinki itd.

Dakle, kod oduzimanja decimalnih razlomaka uočava se sljedeći redoslijed: oduzimanje se potpisuje ispod reduciranog tako da su iste znamenke jedna ispod druge, a svi zarezi u istom okomitom stupcu; na desnoj strani pripisuju, barem mentalno, u smanjenom ili oduzimanom toliko nula tako da imaju isti broj znamenki, zatim oduzimaju znamenkama, počevši od desne strane, i u dobivenoj razlici stavljaju zarez u isti okomiti stupac u kojem se nalazi u smanjenom i oduzetom.

§ 109. Množenje decimalnih razlomaka.

Razmotrimo nekoliko primjera množenja decimalnih razlomaka.

Da bismo pronašli umnožak ovih brojeva, možemo zaključiti na sljedeći način: ako se faktor poveća za 10 puta, tada će oba faktora biti cijeli brojevi i onda ih možemo množiti prema pravilima za množenje cijelih brojeva. Ali znamo da kada se jedan od faktora poveća nekoliko puta, proizvod se povećava za isti iznos. To znači da je broj koji proizlazi iz množenja cjelobrojnih faktora, tj. 28 s 23, 10 puta veći od pravog umnoška, ​​a da biste dobili pravi umnožak, potrebno je pronađeni umnožak smanjiti za 10 puta. Stoga ovdje morate jednom izvesti množenje s 10 i jednom dijeljenje s 10, ali množenje i dijeljenje s 10 se izvodi pomicanjem zareza udesno i ulijevo za jedan znak. Stoga morate učiniti ovo: u množitelju pomaknite zarez udesno za jedan znak, od toga će biti jednako 23, a zatim morate pomnožiti rezultirajuće cijele brojeve:

Ovaj proizvod je 10 puta veći od pravog. Stoga se mora smanjiti za 10 puta, za što pomičemo zarez za jedan znak ulijevo. Dakle, dobivamo

28 2,3 = 64,4.

U svrhu provjere, možete napisati decimalni razlomak s nazivnikom i izvršiti radnju prema pravilu za množenje običnih razlomaka, t.j.

2) 12,27 0,021.

Razlika između ovog i prethodnog primjera je u tome što su ovdje oba faktora predstavljena decimalnim razlomcima. Ali ovdje, u procesu množenja, nećemo obraćati pažnju na zareze, odnosno privremeno ćemo povećati množitelj za 100 puta, a množitelj za 1000 puta, što će povećati umnožak za 100 000 puta. Dakle, množenjem 1227 s 21, dobivamo:

1 227 21 = 25 767.

Uzimajući u obzir da je dobiveni proizvod 100.000 puta veći od pravog, sada ga moramo smanjiti za 100.000 puta pravilnim stavljanjem zareza u njega, tada dobivamo:

32,27 0,021 = 0,25767.

Provjerimo:

Dakle, da bi se dva decimalna razlomka pomnožili, dovoljno je, ne obazirući se na zareze, pomnožiti ih kao cijele brojeve i u umnošku odvojiti zarezom na desnoj strani onoliko decimalnih mjesta koliko je bilo u množeniku i u faktor zajedno.

U posljednjem primjeru rezultat je proizvod s pet decimalnih mjesta. Ako takva veća preciznost nije potrebna, tada se vrši zaokruživanje. decimalni razlomak. Prilikom zaokruživanja trebali biste koristiti isto pravilo koje je naznačeno za cijele brojeve.

§ 110. Množenje pomoću tablica.

Množenje decimala ponekad se može obaviti pomoću tablica. U tu svrhu možete, na primjer, koristiti te tablice množenja dvoznamenkasti brojevi, čiji je opis dat ranije.

1) Pomnožite 53 s 1,5.

Pomnožit ćemo 53 s 15. U tablici je ovaj umnožak jednak 795. Našli smo umnožak 53 sa 15, ali je naš drugi faktor bio 10 puta manji, što znači da se umnožak mora smanjiti za 10 puta, t.j.

53 1,5 = 79,5.

2) Pomnožite 5,3 sa 4,7.

Prvo, u tablici nalazimo umnožak 53 sa 47, to će biti 2491. Ali budući da smo množitelj i množitelj povećali ukupno 100 puta, onda je rezultirajući umnožak 100 puta veći nego što bi trebao biti; pa moramo smanjiti ovaj proizvod za faktor 100:

5,3 4,7 = 24,91.

3) Pomnožite 0,53 sa 7,4.

Prvo u tablici nalazimo umnožak 53 sa 74; ovo će biti 3922. Ali budući da smo množitelj povećali za 100 puta, a množitelj za 10 puta, umnožak se povećao za 1000 puta; pa ga sada moramo smanjiti za faktor 1000:

0,53 7,4 = 3,922.

§ 111. Podjela decimala.

Decimalno dijeljenje ćemo pogledati ovim redoslijedom:

1. Decimalno dijeljenje po cijeli broj,

1. Dijeljenje decimalnog razlomka cijelim brojem.

1) Podijelite 2,46 sa 2.

Podijelili smo s 2 prva cijela broja, zatim desetine i na kraju stotinke.

2) Podijelite 32,46 sa 3.

32,46: 3 = 10,82.

Podijelili smo 3 desetice s 3, zatim smo počeli dijeliti 2 jedinice s 3; budući da je broj jedinica dividende (2) manji djelitelj(3), tada sam morao staviti 0 u kvocijent; dalje, na ostatak smo srušili 4 desetine i podijelili 24 desetine sa 3; dobio privatno 8 desetina i na kraju podijelio 6 stotinki.

3) Podijelite 1,2345 sa 5.

1,2345: 5 = 0,2469.

Ovdje, u prvom redu kvocijenta, ispalo je nula cijelih brojeva, jer jedan cijeli broj nije djeljiv s 5.

4) Podijelite 13,58 sa 4.

Posebnost ovog primjera je da kada smo privatno dobili 9 stotinki, onda se našao ostatak od 2 stotinke, taj ostatak smo podijelili na tisućinke, dobili 20 tisućinki i priveli podjelu kraju.

Pravilo. Dijeljenje decimalnog razlomka cijelim brojem provodi se na isti način kao i dijeljenje cijelih brojeva, a dobiveni ostaci se pretvaraju u decimalne razlomke, sve manje; dijeljenje se nastavlja sve dok ostatak ne bude nula.

2. Dijeljenje decimalnog razlomka decimalnim razlomkom.

1) Podijelite 2,46 s 0,2.

Već znamo podijeliti decimalni razlomak cijelim brojem. Razmislimo može li se i ovaj novi slučaj podjele svesti na prethodni? Svojedobno smo razmatrali izvanredno svojstvo kvocijenta, koje se sastoji u tome da ostaje nepromijenjen dok se dividendu i djelitelj povećava ili smanjuje za isti broj puta. Lako bismo izvršili dijeljenje ponuđenih brojeva da je djelitelj cijeli broj. Da biste to učinili, dovoljno ga je povećati 10 puta, a za dobivanje točnog kvocijenta potrebno je dividendu povećati za isti broj puta, odnosno 10 puta. Tada će se dijeljenje ovih brojeva zamijeniti dijeljenjem takvih brojeva:

i nema potrebe za bilo kakvim amandmanima nasamo.

Napravimo ovu podjelu:

Dakle 2,46: 0,2 = 12,3.

2) Podijelite 1,25 sa 1,6.

Povećamo djelitelj (1.6) za 10 puta; da se kvocijent ne promijeni, povecamo dividendu za 10 puta; 12 cijelih brojeva nije djeljivo sa 16, pa upišemo u kvocijent 0 i podijelimo 125 desetinki sa 16, dobijemo 7 desetina u kvocijentu, a ostatak je 13. 13 desetinki podijelimo na stotinke dodjeljivanjem nule i 130 stotinki, itd. podijelimo sa 16 . Obratite pažnju na sljedeće:

a) kada se u kvocijentu ne dobivaju cijeli brojevi, tada se na njihovo mjesto upisuju nula cijeli brojevi;

b) kada se nakon uzimanja znamenke dividende u ostatak dobije broj koji nije djeljiv djeliteljem, tada se u kvocijent upisuje nula;

c) kada, nakon što se ukloni posljednja znamenka dividende, dijeljenje ne završi, tada se ostatcima dodjeljuje nula, dijeljenje se nastavlja;

d) ako je dividenda cijeli broj, tada se pri dijeljenju decimalnim razlomkom njegovo povećanje provodi dodjeljivanjem nula.

Dakle, da biste broj podijelili decimalnim razlomkom, trebate odbaciti zarez u djelitelju, a zatim povećati dividendu onoliko puta koliko se djelitelj povećao kada je zarez u njemu ispušten, a zatim izvršiti dijeljenje prema pravilo dijeljenja decimalnog razlomka cijelim brojem.

§ 112. Približni kvocijent.

U prethodnom odlomku razmatrali smo dijeljenje decimalnih razlomaka, a u svim primjerima koje smo rješavali dijeljenje je dovedeno do kraja, odnosno dobiven je točan kvocijent. Međutim, u većini slučajeva se ne može dobiti točan kvocijent, koliko god proširili podjelu. Evo jednog takvog slučaja: Podijelite 53 sa 101.

Već smo dobili pet znamenki u kvocijentu, ali dijeljenje još nije završilo i nema nade da će ikada završiti, jer se u ostatku počinju pojavljivati ​​brojevi koje smo prije upoznali. Brojevi će se također ponavljati u kvocijentu: očito, nakon broja 7 pojavit će se broj 5, zatim 2 i tako bez kraja. U takvim slučajevima dijeljenje se prekida i ograničava na prvih nekoliko znamenki kvocijenta. Ovo privatno se zove približan. Kako izvršiti dijeljenje u ovom slučaju, pokazat ćemo na primjerima.

Neka se zahtijeva dijeljenje 25 s 3. Očito je da se takvim dijeljenjem ne može dobiti točan kvocijent izražen kao cijeli broj ili decimalni razlomak. Stoga ćemo tražiti približni kvocijent:

25: 3 = 8 i ostatak 1

Približni kvocijent je 8; to je, naravno, manji od točnog kvocijenta, jer postoji ostatak od 1. Da biste dobili točan kvocijent, potrebno je pronađenom približnom količniku, odnosno 8, dodati razlomak koji nastaje dijeljenjem ostatka , jednako 1, sa 3; to će biti razlomak 1/3. To znači da će točan kvocijent biti izražen kao mješoviti broj 8 1 / 3 . Budući da je 1/3 pravi razlomak, tj. razlomak, manje od jedan, onda, odbacujući ga, pretpostavljamo pogreška, koji manje od jedan . Privatni 8 će približni kvocijent do jedan s nedostatkom. Ako uzmemo 9 umjesto 8, tada dopuštamo i grešku manju od jedan, jer ćemo dodati ne cijelu jedinicu, već 2/3. Takva privatna oporuka približni kvocijent do jedan s viškom.

Uzmimo sad još jedan primjer. Neka je potrebno podijeliti 27 sa 8. Budući da ovdje nećemo dobiti točan kvocijent izražen kao cijeli broj, tražit ćemo približni kvocijent:

27: 8 = 3 i ostatak 3.

Ovdje je pogreška 3/8, manja je od jedan, što znači da se približni kvocijent (3) nalazi do jedan s nedostatkom. Nastavljamo podjelu: ostatak od 3 podijelimo na desetine, dobijemo 30 desetina; Podijelimo ih sa 8.

Privatno smo dobili na licu mjesta desetinke 3, a u ostatku b desetinke. Ako se posebno ograničimo na broj 3.3, a ostatak 6 odbacimo, tada ćemo dopustiti pogrešku manju od jedne desetine. Zašto? Budući da bi se točan kvocijent dobio kada bismo 3,3 dodali rezultat dijeljenja 6 desetinki s 8; iz ove podjele bilo bi 6/80, što je manje od jedne desetine. (Provjeri!) Dakle, ako se ograničimo na desetinke u količniku, onda možemo reći da smo pronašli kvocijent točno do jedne desetine(s nedostatkom).

Nastavimo dijeljenje kako bismo pronašli još jedno decimalno mjesto. Da bismo to učinili, podijelimo 6 desetina na stotinke i dobijemo 60 stotinki; Podijelimo ih sa 8.

Privatno na trećem mjestu ispalo je 7, a u ostatku 4 stotinke; ako ih odbacimo, tada dopuštamo pogrešku manju od jedne stotinke, jer je 4 stotinke podijeljeno s 8 manje od jedne stotinke. U takvim slučajevima kaže se da je kvocijent pronađen. točno do jedne stotinke(s nedostatkom).

U primjeru koji sada razmatramo, možete dobiti točan kvocijent, izražen kao decimalni razlomak. Da biste to učinili, dovoljno je posljednji ostatak, 4 stotinke, podijeliti na tisućinke i podijeliti s 8.

Međutim, u velikoj većini slučajeva nemoguće je dobiti točan kvocijent i treba se ograničiti na njegove približne vrijednosti. Sada ćemo razmotriti takav primjer:

40: 7 = 5,71428571...

Točke na kraju broja označavaju da podjela nije završena, odnosno da je jednakost približna. Obično se približna jednakost piše ovako:

40: 7 = 5,71428571.

Uzeli smo kvocijent s osam decimalnih mjesta. Ali ako nije potrebna tako velika preciznost, može se ograničiti na cijeli dio kvocijenta, tj. na broj 5 (točnije, 6); za veću točnost mogle bi se uzeti u obzir desetine i uzeti kvocijent jednak 5,7; ako je iz nekog razloga ta točnost nedovoljna, onda se možemo zaustaviti na stotinkama i uzeti 5,71 itd. Ispišimo pojedinačne količnike i nazovimo ih.

Prvi približni kvocijent do jedan 6.

Drugi » » » do jedne desetine 5.7.

Treći » » » do stotke 5,71.

Četvrti » » » do jedne tisućinke od 5.714.

Dakle, da bi se pronašao približni kvocijent s točnošću od neke, na primjer, 3. decimale (tj. do jedne tisućinke), dijeljenje se prekida čim se pronađe ovaj znak. U tom slučaju treba zapamtiti pravilo izneseno u § 40.

§ 113. Najjednostavniji zadaci za kamate.

Nakon proučavanja decimalnih razlomaka riješit ćemo još nekoliko postotnih zadataka.

Ovi problemi su slični onima koje smo rješavali na odjelu običnih razlomaka; ali sada ćemo stotinke zapisivati ​​u obliku decimalnih razlomaka, odnosno bez izričito označenog nazivnika.

Prije svega, morate se moći jednostavno prebaciti s običnog razlomka na decimalni razlomak s nazivnikom 100. Da biste to učinili, trebate podijeliti brojnik s nazivnikom:

Donja tablica pokazuje kako se broj sa simbolom % (postotak) zamjenjuje decimalom s nazivnikom 100:

Razmotrimo sada nekoliko problema.

1. Pronalaženje postotaka zadanog broja.

Zadatak 1. U jednom selu živi samo 1600 ljudi. Broj djece školske dobi iznosi 25%. ukupni broj stanovnika. Koliko djece školske dobi ima u ovom selu?

U ovom zadatku morate pronaći 25% ili 0,25 od 1600. Problem se rješava množenjem:

1.600 0,25 = 400 (djeca).

Dakle, 25% od 1.600 je 400.

Za jasno razumijevanje ovog zadatka, korisno je podsjetiti da na svaku stotinu stanovništva dolazi 25 djece školske dobi. Stoga, da biste pronašli broj sve djece školske dobi, prvo možete saznati koliko je stotina u broju 1600 (16), a zatim pomnožite 25 s brojem stotina (25 x 16 = 400). Na taj način možete provjeriti valjanost rješenja.

Zadatak 2.Štedionice daju štedišama 2% prihoda godišnje. Koliki će prihod godišnje dobiti deponent koji je položio: a) 200 rubalja? b) 500 rubalja? c) 750 rubalja? d) 1000 rubalja?

U sva četiri slučaja, da bi se riješio problem, bit će potrebno izračunati 0,02 od navedenih iznosa, odnosno svaki od ovih brojeva morat će se pomnožiti s 0,02. Učinimo to:

a) 200 0,02 = 4 (rubalji),

b) 500 0,02 = 10 (rubalji),

c) 750 0,02 = 15 (rubalji),

d) 1.000 0,02 = 20 (rubalji).

Svaki od ovih slučajeva može se provjeriti sljedećim razmatranjima. Štedionice daju štedišama 2% prihoda, odnosno 0,02 iznosa uloženog u štednju. Ako je iznos bio 100 rubalja, tada bi 0,02 od toga bilo 2 rublje. To znači da svaka stota donosi deponentu 2 rublje. prihod. Stoga je u svakom od razmatranih slučajeva dovoljno shvatiti koliko je stotina u danom broju i pomnožiti 2 rublje s tim brojem stotina. U primjeru a) stotine 2, dakle

2 2 \u003d 4 (rubalji).

U primjeru d) stotine su 10, što znači

2 10 \u003d 20 (rubalji).

2. Pronalaženje broja po postotku.

Zadatak 1. U proljeće je školu završila 54 učenika, što je 6% od ukupnog broja učenika. Koliko je učenika bilo u školi u prošlosti akademska godina?

Najprije razjasnimo značenje ovog problema. Školu je završilo 54 učenika, što je 6% od ukupnog broja učenika, odnosno 6 stotinki (0,06) svih učenika u školi. To znači da znamo dio učenika izražen brojem (54) i razlomkom (0,06), a iz tog razlomka moramo pronaći cijeli broj. Dakle, pred nama je običan problem pronalaženja broja po razlomku (§ 90, str. 6). Problemi ove vrste rješavaju se dijeljenjem:

To znači da je u školi bilo 900 učenika.

Korisno je takve probleme provjeriti rješavanjem inverznog zadatka, tj. nakon rješavanja problema, barem u mislima, treba riješiti problem prve vrste (pronalaženje postotka zadanog broja): uzeti pronađeni broj ( 900) kao što je zadano i iz njega pronađite postotak naveden u riješenom zadatku, i to:

900 0,06 = 54.

Zadatak 2. Obitelj potroši 780 rubalja na hranu tijekom mjeseca, što je 65% mjesečnog prihoda oca. Odredite njegov mjesečni prihod.

Ovaj zadatak ima isto značenje kao i prethodni. Daje dio mjesečne zarade, izražen u rubljama (780 rubalja), i označava da taj dio iznosi 65%, odnosno 0,65, ukupne zarade. A željena je cijela zarada:

780: 0,65 = 1 200.

Stoga je željena zarada 1200 rubalja.

3. Pronalaženje postotka brojeva.

Zadatak 1.Školska knjižnica ima ukupno 6000 knjiga. Među njima je 1200 knjiga iz matematike. Koliki postotak knjiga iz matematike čini ukupan broj knjiga u knjižnici?

Već smo razmatrali (§97) probleme ove vrste i došli do zaključka da za izračunavanje postotka dvaju brojeva trebate pronaći omjer tih brojeva i pomnožiti ga sa 100.

U našem zadatku trebamo pronaći postotak brojeva 1.200 i 6.000.

Prvo pronađemo njihov omjer, a zatim ga pomnožimo sa 100:

Dakle, postotak brojeva 1200 i 6000 je 20. Drugim riječima, knjige iz matematike čine 20% ukupnog broja svih knjiga.

Za provjeru rješavamo inverzni problem: pronađite 20% od 6000:

6 000 0,2 = 1 200.

Zadatak 2. Postrojenje bi trebalo dobiti 200 tona ugljena. Isporučeno je već 80 tona.Koliki je postotak ugljena isporučen u postrojenje?

Ovaj problem pita koliki je postotak jedan broj (80) od drugog (200). Omjer ovih brojeva bit će 80/200. Pomnožimo to sa 100:

To znači da je isporučeno 40% ugljena.

U ovom članku analizirat ćemo tako važnu radnju s decimalnim razlomcima kao što je podjela. Prvo formuliramo generalni principi, zatim ćemo analizirati kako pravilno podijeliti decimalne razlomke po stupcu i na druge razlomke i na prirodne brojeve. Zatim ćemo analizirati podjelu običnih razlomaka na decimale i obrnuto, a na kraju ćemo vidjeti kako pravilno podijeliti razlomke koji završavaju na 0, 1, 0, 01, 100, 10 itd.

Ovdje uzimamo samo slučajeve s pozitivnim razlomcima. Ako se ispred razlomka nalazi minus, onda da biste postupili s njim, morate proučiti materijal o podjeli racionalnih i realnih brojeva.

Yandex.RTB R-A-339285-1

Svi decimalni razlomci, i konačni i periodični, samo su poseban oblik pisanja običnih razlomaka. Stoga se za njih primjenjuju isti principi kao i za njihove odgovarajuće obične razlomke. Dakle, cijeli proces dijeljenja decimalnih razlomaka svodimo na njihovu zamjenu s običnim, nakon čega slijedi izračunavanje nama već poznatim metodama. Uzmimo konkretan primjer.

Primjer 1

Podijelite 1,2 sa 0,48.

Odluka

Decimalne razlomke zapisujemo u obliku običnih razlomaka. Moći ćemo:

1 , 2 = 12 10 = 6 5

0 , 48 = 48 100 = 12 25 .

Dakle, trebamo podijeliti 6 5 sa 12 25 . Vjerujemo:

1, 2: 0, 48 = 6 2: 12 25 = 6 5 25 12 = 6 25 5 12 = 5 2

Iz dobivenog nepravilan razlomak možete odabrati cijeli dio i dobiti mješoviti broj 2 1 2, ili ga možete predstaviti kao decimalni razlomak tako da odgovara izvornim brojevima: 5 2 \u003d 2, 5. Kako to učiniti, već smo pisali ranije.

Odgovor: 1 , 2: 0 , 48 = 2 , 5 .

Primjer 2

Izračunaj koliko će biti 0 , (504) 0 , 56 .

Odluka

Prvo, periodični decimalni razlomak moramo pretvoriti u obični.

0 , (504) = 0 , 504 1 - 0 , 001 = 0 , 504 0 , 999 = 504 999 = 56 111

Nakon toga ćemo također prevesti konačni decimalni razlomak u drugi oblik: 0, 56 = 56 100. Sada imamo dva broja s kojima će nam biti lako izvršiti potrebne izračune:

0 , (504) : 1 , 11 = 56 111: 56 100 = 56 111 100 56 = 100 111

Imamo rezultat koji također možemo pretvoriti u decimalni. Da biste to učinili, podijelite brojnik s nazivnikom koristeći metodu stupca:

Odgovor: 0 , (504) : 0 , 56 = 0 , (900) .

Ako smo u primjeru dijeljenja susreli neperiodične decimalne razlomke, tada ćemo postupiti malo drugačije. Ne možemo ih dovesti na uobičajene obične razlomke, pa ih pri dijeljenju prvo moramo zaokružiti na određenu znamenku. Ova radnja se mora izvesti i s dividendom i s djeliteljem: također ćemo zaokružiti postojeći konačni ili periodični razlomak u interesu točnosti.

Primjer 3

Pronađite koliko će biti 0, 779 ... / 1, 5602.

Odluka

Prije svega, oba razlomka zaokružujemo na stotinke. Ovako prelazimo s beskonačnih neponavljajućih razlomaka na konačne decimale:

0 , 779 … ≈ 0 , 78

1 , 5602 ≈ 1 , 56

Možemo nastaviti s izračunima i dobiti približan rezultat: 0, 779 ...: 1, 5602 ≈ 0, 78: 1, 56 = 78100: 156100 = 78100 100156 = 78156 = 12 = 0,5.

Točnost rezultata ovisit će o stupnju zaokruživanja.

Odgovor: 0 , 779 … : 1 , 5602 ≈ 0 , 5 .

Kako podijeliti prirodni broj s decimalom i obrnuto

Pristup dijeljenju u ovom slučaju je gotovo isti: konačne i periodične razlomke zamjenjujemo običnim, a beskonačne neperiodične zaokružujemo. Počnimo s primjerom dijeljenja prirodnim brojem i decimalnim razlomkom.

Primjer 4

Podijelite 2,5 sa 45.

Odluka

Dovedemo 2, 5 u oblik običnog razlomka: 255 10 \u003d 51 2. Zatim ga samo trebamo podijeliti na prirodni broj. Već znamo kako to učiniti:

25, 5: 45 = 51 2: 45 = 51 2 1 45 = 17 30

Ako rezultat prevedemo u decimalni zapis, dobivamo 0 , 5 (6) .

Odgovor: 25 , 5: 45 = 0 , 5 (6) .

Metoda dijeljenja po stupcu dobra je ne samo za prirodne brojeve. Po analogiji, možemo ga koristiti i za razlomke. U nastavku ćemo navesti slijed radnji koje je potrebno izvršiti za to.

Definicija 1

Da biste stupac decimalnih razlomaka podijelili prirodnim brojevima, morate:

1. Dodajte nekoliko nula decimalnom razlomku s desne strane (za dijeljenje možemo dodati bilo koji broj njih koji nam je potreban).

2. Podijelite decimalni razlomak prirodnim brojem pomoću algoritma. Kada se dijeljenje cjelobrojnog dijela razlomka završi, u dobiveni kvocijent stavljamo zarez i dalje brojimo.

Rezultat takvog dijeljenja može biti ili konačan ili beskonačan periodični decimalni razlomak. Ovisi o ostatku: ako je nula, tada će rezultat biti konačan, a ako se ostaci počnu ponavljati, odgovor će biti periodični razlomak.

Uzmimo nekoliko zadataka kao primjer i pokušajmo dovršiti ove korake određenim brojevima.

Primjer 5

Izračunaj koliko će biti 65 , 14 4 .

Odluka

Koristimo metodu stupaca. Da biste to učinili, dodajte dvije nule razlomku i dobit ćete decimalni razlomak 65, 1400, koji će biti jednak izvorniku. Sada pišemo stupac za dijeljenje sa 4:

Rezultirajući broj bit će rezultat dijeljenja cijelog broja koji nam je potreban. Stavljamo zarez odvajajući ga i nastavljamo:

Došli smo do nulte vrijednosti, dakle, proces dijeljenja je završen.

Odgovor: 65 , 14: 4 = 16 , 285 .

Primjer 6

Podijelite 164,5 sa 27.

Odluka

Prvo podijelimo frakcijski dio i dobijemo:

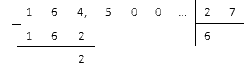
Dobivenu figuru odvajamo zarezom i nastavljamo dijeliti:

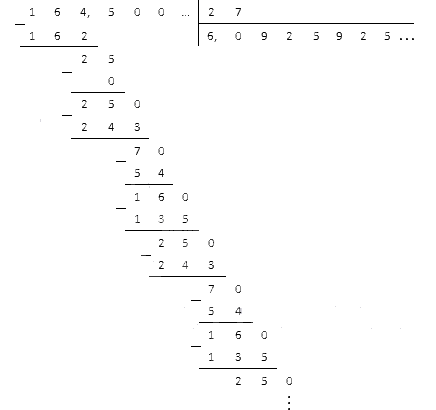
Vidimo da su se ostaci počeli periodično ponavljati, a brojevi devet, dva i pet počeli su se izmjenjivati ​​u kvocijentu. Tu ćemo se zaustaviti i odgovor napisati kao periodični razlomak 6, 0 (925) .

Odgovor: 164 , 5: 27 = 6 , 0 (925) .

Takva se podjela može svesti na proces pronalaženja privatnog decimalnog razlomka i prirodnog broja koji je već opisan. Da bismo to učinili, trebamo pomnožiti dividendu i djelitelj s 10, 100 itd. tako da se djelitelj pretvori u prirodan broj. Zatim izvodimo gornji slijed radnji. Ovaj pristup je moguć zbog svojstava dijeljenja i množenja. U doslovnom obliku, napisali smo ih ovako:

a: b = (a 10) : (b 10) , a: b = (a 100) : (b 100) i tako dalje.

Formulirajmo pravilo:

Definicija 2

Da biste jedan konačni decimalni razlomak podijelili s drugim, morate:

1. Pomaknite zarez u djelitelju i djelitelju udesno za broj znakova koji je potreban da se djelitelj pretvori u prirodan broj. Ako u dividendi nema dovoljno znakova, dodajemo joj nule na desnoj strani.

2. Nakon toga dijelimo razlomak stupcem s rezultirajućim prirodnim brojem.

Pogledajmo konkretan problem.

Primjer 7

Podijelite 7, 287 sa 2, 1.

Rješenje: Da bi djelitelj postao prirodan broj, trebamo pomaknuti zarez za jedan znak udesno. Tako smo prešli na dijeljenje decimalnog razlomka 72, 87 s 21. Dobivene brojeve zapišimo u stupac i izračunajmo

Odgovor: 7 , 287: 2 , 1 = 3 , 47

Primjer 8

Izračunaj 16 , 3 0 , 021 .

Odluka

Zarez ćemo morati pomaknuti na tri znamenke. Za to nema dovoljno brojeva u djelitelju, pa morate koristiti dodatne nule. Mislimo da će krajnji rezultat biti:

Vidimo periodično ponavljanje ostataka 4 , 19 , 1 , 10 , 16 , 13 . Kvocijent se ponavlja 1, 9, 0, 4, 7 i 5. Tada je naš rezultat periodična decimala 776 , (190476) .

Odgovor: 16 , 3: 0 , 021 = 776 , (190476) ​​​​​​

Metoda koju smo opisali omogućuje vam da učinite suprotno, odnosno podijelite prirodni broj konačnim decimalnim razlomkom. Pogledajmo kako se to radi.

Primjer 9

Izračunaj koliko će biti 3 5 , 4 .

Odluka

Očito ćemo morati pomaknuti zarez udesno za jedan znak. Nakon toga možemo početi dijeliti 30, 0 sa 54. Zapišimo podatke u stupac i izračunajmo rezultat:

Ponavljanjem ostatka dobivamo broj 0 , (5) , koji je periodična decimala.

Odgovor: 3: 5 , 4 = 0 , (5) .

Kako podijeliti decimale sa 1000, 100, 10 itd.

Prema već proučenim pravilima za dijeljenje običnih razlomaka, dijeljenje razlomka na desetke, stotine, tisuće slično je množenju s 1/1000, 1/100, 1/10 itd. Ispada da bi se izvršilo dijeljenje , u ovom slučaju, dovoljno je samo pomaknuti zarez na pravi iznos znamenke. Ako u broju nema dovoljno vrijednosti za prijenos, morate dodati potreban broj nula.

Primjer 10

Dakle, 56, 21: 10 = 5, 621 i 0, 32: 100 000 = 0, 0000032.

U slučaju beskonačnih decimala činimo isto.

Primjer 11

Na primjer, 3 , (56) : 1000 = 0 , 003 (56) i 593 , 374 ... : 100 = 5 , 93374 ... .

Kako podijeliti decimale s 0,001, 0,01, 0,1 itd.

Koristeći isto pravilo, također možemo podijeliti razlomke prema navedenim vrijednostima. Ova će radnja biti slična množenju s 1000 , 100 , 10 . Da bismo to učinili, pomičemo zarez na jednu, dvije ili tri znamenke, ovisno o uvjetima problema, i dodajemo nule ako u broju nema dovoljno znamenki.

Primjer 12

Na primjer, 5, 739: 0, 1 = 57, 39 i 0, 21: 0, 00001 = 21 000.

Ovo pravilo vrijedi i za beskonačne decimale. Savjetujemo samo da pripazite na period razlomka koji se dobije u odgovoru.

Dakle, 7 , 5 (716) : 0 , 01 = 757 , (167) , jer nakon što smo pomaknuli zarez u decimalnom zapisu 7 , 5716716716 ... dvije znamenke udesno, dobili smo 757 , 167167 ... .

Ako u primjeru imamo neperiodične razlomke, onda je sve jednostavnije: 394 , 38283 ... : 0 , 001 = 394382 , 83 ... .

Kako podijeliti mješoviti broj ili obični razlomak s decimalom i obrnuto

Ovu radnju također svodimo na operacije s običnim razlomcima. Da biste to učinili, morate zamijeniti decimalni brojevi odgovarajuće obične razlomke, a mješoviti broj zapiši kao nepravilan razlomak.

Ako neperiodični razlomak podijelimo običnim ili mješovitim brojem, moramo učiniti suprotno, zamijenivši obični razlomak ili mješoviti broj s odgovarajućim decimalnim razlomkom.

Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter

Pronađite prvu znamenku kvocijenta (rezultat dijeljenja). Da biste to učinili, podijelite prvu znamenku dividende s djeliteljem. Rezultat upiši ispod djelitelja.

• U našem primjeru, prva znamenka dividende je 3. Podijelite 3 s 12. Budući da je 3 manje od 12, tada će rezultat dijeljenja biti 0. Upišite 0 ispod djelitelja - ovo je prva znamenka kvocijenta.

Razmotrite primjere dijeljenja decimala u ovom svjetlu.

Primjer.

Podijelite decimalu 1,2 s decimalom 0,48.

Odluka.

Odgovor:

1,2:0,48=2,5 .

Primjer.

Podijelite periodičnu decimalu 0.(504) s decimalom 0,56 .

Odluka.

Prevedimo periodični decimalni razlomak u obični:. Također prevodimo konačni decimalni razlomak 0,56 u obični, imamo 0,56 \u003d 56/100. Sada možemo prijeći s dijeljenja izvornih decimala na dijeljenje običnih razlomaka i završiti izračune: .

Prevedimo rezultirajući obični razlomak u decimalni razlomak dijeljenjem brojnika s nazivnikom u stupcu:

Odgovor:

0,(504):0,56=0,(900) .

Princip dijeljenja beskonačnih neperiodičnih decimalnih razlomaka razlikuje se od principa dijeljenja konačnih i periodičnih decimalnih razlomaka, budući da se decimalni razlomci koji se ne ponavljaju ne mogu pretvoriti u obične razlomke. Dijeljenje beskonačnih neperiodičnih decimalnih razlomaka svodi se na dijeljenje konačnih decimalnih razlomaka, za koje se provodi zaokruživanje brojeva do određene razine. Štoviše, ako je jedan od brojeva s kojima se provodi dijeljenje konačni ili periodični decimalni razlomak, tada se također zaokružuje na istu znamenku kao i neperiodični decimalni razlomak.

Primjer.

Podijelite beskonačnu neponavljajuću decimalu 0,779... sa završnom decimalom 1,5602.

Odluka.

Prvo morate zaokružiti decimalne razlomke kako biste prešli s dijeljenja beskonačnog neponavljajućeg decimalnog razlomka na dijeljenje konačnih decimalnih razlomaka. Možemo zaokružiti na stotinke: 0,779…≈0,78 i 1,5602≈1,56. Dakle, 0,779…:1,5602≈0,78:1,56= 78/100:156/100=78/100 100/156= 78/156=1/2=0,5 .

Odgovor:

0,779…:1,5602≈0,5 .

Dijeljenje prirodnog broja s decimalnim razlomkom i obrnuto

Bit pristupa dijeljenju prirodnog broja decimalnim razlomkom i dijeljenju decimalnog razlomka prirodnim brojem ne razlikuje se od suštine dijeljenja decimalnih razlomaka. To jest, konačni i periodični razlomci se zamjenjuju običnim razlomcima, a beskonačni neperiodični razlomci se zaokružuju.

Za ilustraciju, razmotrite primjer dijeljenja decimalnog razlomka prirodnim brojem.

Primjer.

Podijelite decimalni razlomak 25,5 prirodnim brojem 45.

Odluka.

Zamjenom decimalnog razlomka 25,5 običnim razlomkom 255/10=51/2, dijeljenje se svodi na dijeljenje običnog razlomka prirodnim brojem: . Rezultirajući razlomak u decimalnom zapisu je 0,5(6) .

Odgovor:

25,5:45=0,5(6) .

Dijeljenje decimalnog razlomka prirodnim brojem po stupcu

Dijeljenje konačnih decimalnih razlomaka prirodnim brojevima prikladno se provodi stupcem po analogiji s dijeljenjem stupcem prirodnih brojeva. Ovdje je pravilo dijeljenja.

Do podijeliti decimalu prirodnim brojem stupcem, potrebno:

• dodajte nekoliko znamenki desno u djeljivi decimalni razlomak 0, (tijekom dijeljenja, ako je potrebno, možete dodati bilo koji broj nula, ali ove nule možda neće biti potrebne);
• izvršite dijeljenje stupcem decimalnog razlomka prirodnim brojem prema svim pravilima za dijeljenje stupcem prirodnih brojeva, ali kada je dijeljenje cjelobrojnog dijela decimalnog razlomka završeno, tada u privatnom trebate stavite zarez i nastavite dijeljenje.

Recimo odmah da se kao rezultat dijeljenja konačnog decimalnog razlomka prirodnim brojem može dobiti ili konačni decimalni razlomak ili beskonačni periodični decimalni razlomak. Doista, nakon dijeljenja svih decimalnih mjesta djeljivog razlomka osim 0, možemo dobiti ili ostatak 0, i dobit ćemo konačni decimalni razlomak, ili će se ostatak početi periodično ponavljati i dobit ćemo periodični decimalni razlomak frakcija.

Pozabavimo se svim zamršenostima dijeljenja decimalnih razlomaka na prirodne brojeve stupcem prilikom rješavanja primjera.

Primjer.

Podijelite decimalni broj 65,14 s 4.

Odluka.

Izvršimo dijeljenje decimalnog razlomka prirodnim brojem po stupcu. Dodajmo par nula desno u zapisu razlomka 65,14, dok dobijemo decimalni razlomak jednak njemu 65,1400 (vidi jednaki i nejednaki decimalni razlomci). Sada možete početi dijeliti cijeli broj decimalnog razlomka 65,1400 prirodnim brojem 4 u stupcu:

Time je dovršeno dijeljenje cjelobrojnog dijela decimalnog razlomka. Ovdje privatno trebate staviti decimalni zarez i nastaviti dijeljenje:

Došli smo do ostatka od 0, u ovoj fazi završava podjela po stupcu. Kao rezultat, imamo 65,14:4=16,285.

Odgovor:

65,14:4=16,285 .

Primjer.

Podijelite 164,5 sa 27.

Odluka.

Podijelimo decimalni razlomak prirodnim brojem stupcem. Nakon dijeljenja cjelobrojnog dijela, dobivamo sljedeću sliku:

Sada stavljamo zarez privatno i nastavljamo podjelu stupcem:

Sada se jasno vidi da su se ostaci 25, 7 i 16 počeli ponavljati, dok se brojevi 9, 2 i 5 ponavljaju u kvocijentu. Dakle, dijeljenje decimalnog broja 164,5 sa 27 daje nam periodičnu decimalu 6,0(925) .

Odgovor:

164,5:27=6,0(925) .

Podjela decimalnih razlomaka po stupcu

Dijeljenje decimalnog razlomka decimalnim razlomkom može se svesti na dijeljenje decimalnog razlomka prirodnim brojem stupcem. Da biste to učinili, djelitelj i djelitelj moraju se pomnožiti s takvim brojem 10, ili 100, ili 1000, itd., tako da djelitelj postane prirodan broj, a zatim podijeliti prirodnim brojem sa stupcem. To možemo učiniti zbog svojstava dijeljenja i množenja, budući da a:b=(a 10):(b 10) , a:b=(a 100):(b 100) i tako dalje.

Drugim riječima, podijeliti završnu decimalu sa završnom decimalom, potrebno je:

• u djelitelju i djelitelju pomaknite zarez udesno za onoliko znakova koliko ima nakon decimalne zareze u djelitelju, ako u isto vrijeme nema dovoljno znakova u dividendi za pomicanje zareza, tada trebate dodati potreban iznos nule na desnoj strani;
• nakon toga provesti dijeljenje po stupcu decimalnog razlomka prirodnim brojem.

Razmotrimo, prilikom rješavanja primjera, primjenu ovog pravila za dijeljenje decimalnim razlomkom.

Primjer.

Napravite podjelu stupca 7.287 na 2.1.

Odluka.

Pomaknimo zarez u tim decimalnim razlomcima za jednu znamenku udesno, to će nam omogućiti da prijeđemo od dijeljenja decimalnog razlomka 7,287 s decimalnim razlomkom 2,1 do dijeljenja decimalnog razlomka 72,87 prirodnim brojem 21. Podijelimo po stupcu:

Odgovor:

7,287:2,1=3,47 .

Primjer.

Podijelite decimalni broj 16,3 s decimalom 0,021.

Odluka.

Pomaknite zarez u dividendi i djelitelju udesno za 3 znamenke. Očito je da u djelitelju nema dovoljno znamenki za nošenje zareza, pa dodajmo potreban broj nula desno. Sada podijelimo stupac razlomka 16300,0 prirodnim brojem 21:

Od ovog trenutka počinju se ponavljati ostaci 4, 19, 1, 10, 16 i 13, što znači da će se ponavljati i brojevi 1, 9, 0, 4, 7 i 6 u kvocijentu. Kao rezultat, dobivamo periodični decimalni razlomak 776,(190476) .

Odgovor:

16,3:0,021=776,(190476) .

Imajte na umu da vam glasovno pravilo omogućuje dijeljenje prirodnog broja konačnim decimalnim razlomkom u stupcu.

Primjer.

Prirodni broj 3 podijelite s decimalnim razlomkom 5.4.

Odluka.

Nakon što pomaknemo zarez za 1 znamenku udesno, dolazimo do dijeljenja broja 30,0 sa 54. Podijelimo po stupcu:
.

Ovo pravilo se također može primijeniti kada se beskonačni decimalni razlomci dijele s 10, 100, .... Na primjer, 3,(56):1000=0,003(56) i 593,374…:100=5,93374… .

Dijeljenje decimala s 0,1, 0,01, 0,001 itd.

Budući da je 0,1 \u003d 1/10, 0,01 \u003d 1/100 itd., iz pravila dijeljenja običnim razlomkom slijedi da dijeljenje decimalnog razlomka s 0,1, 0,01, 0,001 itd. to je kao da zadanu decimalu množite s 10, 100, 1000 itd. odnosno.

Drugim riječima, da biste decimalni razlomak podijelili s 0,1, 0,01, ... potrebno je pomaknuti zarez udesno za 1, 2, 3, ... znamenke, a ako u decimalnom razlomku nema dovoljno znamenki za pomaknite zarez, tada trebate dodati traženi broj desnim nulama.

Na primjer, 5,739:0,1=57,39 i 0,21:0,00001=21 000 .

Isto pravilo se može primijeniti kada se beskonačne decimale dijele s 0,1, 0,01, 0,001 itd. U ovom slučaju trebate biti vrlo oprezni s dijeljenjem periodičnih razlomaka, kako ne biste pogriješili s periodom razlomka, koji se dobiva kao rezultat dijeljenja. Na primjer, 7,5(716):0,01=757,(167) , budući da nakon pomicanja zareza u zapisu decimalnog razlomka 7,5716716716 ... dvije znamenke udesno, imamo zapis 757,167167 ... . Uz beskonačne neperiodične decimale sve je jednostavnije: 394,38283…:0,001=394382,83… .

Dijeljenje razlomka ili mješovitog broja decimalom i obrnuto

Dijeljenje običnog razlomka ili mješovitog broja konačnim ili periodičnim decimalnim razlomkom, kao i dijeljenje konačnog ili periodičnog decimalnog razlomka običnim razlomkom ili mješovitim brojem, svodi se na dijeljenje običnih razlomaka. Da biste to učinili, decimalni razlomci se zamjenjuju odgovarajućim uobičajenim razlomcima, a mješoviti broj je predstavljen kao nepravilan razlomak.

Kada se beskonačni neperiodični decimalni razlomak dijeli običnim razlomkom ili mješovitim brojem i obrnuto, treba prijeći na dijeljenje decimalnih razlomaka, zamjenjujući obični razlomak ili mješoviti broj odgovarajućim decimalnim razlomkom.

Bibliografija.

• Matematika: studije. za 5 ćelija. opće obrazovanje institucije / N. Ya. Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartsburd. - 21. izd., izbrisano. - M.: Mnemosyne, 2007. - 280 str.: ilustr. ISBN 5-346-00699-0.
• Matematika. 6. razred: udžbenik. za opće obrazovanje institucije / [N. Ya. Vilenkin i drugi]. - 22. izd., vlč. - M.: Mnemosyne, 2008. - 288 str.: ilustr. ISBN 978-5-346-00897-2.
• Algebra: udžbenik za 8 ćelija. opće obrazovanje institucije / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; izd. S. A. Teljakovski. - 16. izd. - M. : Obrazovanje, 2008. - 271 str. : bolestan. - ISBN 978-5-09-019243-9.
• Gusev V. A., Mordkovich A. G. Matematika (priručnik za pristupnike tehničkih škola): Proc. dodatak.- M.; Viša škola, 1984.-351 str., ilustr.

U prošloj lekciji naučili smo kako zbrajati i oduzimati decimalne razlomke (pogledajte lekciju " Zbrajanje i oduzimanje decimalnih razlomaka"). Istodobno su procijenili koliko su izračuni pojednostavljeni u usporedbi s uobičajenim razlomcima na "dva kata".

Nažalost, kod množenja i dijeljenja decimalnih razlomaka ovaj učinak se ne događa. U nekim slučajevima decimalni zapis čak komplicira ove operacije.

Najprije uvedemo novu definiciju. Susrećemo ga dosta često, i to ne samo u ovoj lekciji.

Značajan dio broja je sve između prve i zadnje znamenke koja nije nula, uključujući najave. Govorimo samo o brojevima, decimalna točka se ne uzima u obzir.

Znamenke uključene u značajan dio broja nazivaju se značajnim znamenkama. Mogu se ponavljati i čak biti jednaki nuli.

Na primjer, razmotrite nekoliko decimalnih razlomaka i napišite njihove odgovarajuće značajne dijelove:

1. 91,25 → 9125 (značajne brojke: 9; 1; 2; 5);
2. 0,008241 → 8241 (značajne brojke: 8; 2; 4; 1);
3. 15,0075 → 150075 (značajne brojke: 1; 5; 0; 0; 7; 5);
4. 0,0304 → 304 (značajne brojke: 3; 0; 4);
5. 3000 → 3 (značajna figura samo jedan: 3).

Imajte na umu: nule unutar značajnog dijela broja ne idu nikamo. S nečim sličnim smo se već susreli kada smo naučili pretvarati decimalne razlomke u obične (vidi lekciju “Decimalni razlomci”).

Ova točka je toliko važna, a greške se ovdje čine toliko često da ću objaviti test na ovu temu u bliskoj budućnosti. Svakako vježbajte! A mi, naoružani konceptom značajnog dijela, prijeći ćemo, zapravo, na temu lekcije.

Decimalno množenje

Operacija množenja sastoji se od tri uzastopna koraka:

1. Za svaki razlomak zapišite značajan dio. Dobit ćete dva obična cijela broja - bez nazivnika i decimalnih točaka;
2. Pomnožite ove brojeve s bilo kojim zgodan način. Izravno, ako su brojevi mali, ili u stupcu. Dobivamo značajan dio željenog razlomka;
3. Saznajte gdje se i za koliko znamenki pomiče decimalna točka u izvornim razlomcima kako bi se dobio odgovarajući značajan dio. Izvedite obrnute pomake na značajnom dijelu dobivenom u prethodnom koraku.

Još jednom podsjetim da se nule na stranama značajnog dijela nikada ne uzimaju u obzir. Zanemarivanje ovog pravila dovodi do grešaka.

1. 0,28 12,5;
2. 6,3 1,08;
3. 132,5 0,0034;
4. 0,0108 1600,5;
5. 5,25 10.000.

Radimo s prvim izrazom: 0,28 12,5.

1. Napišimo bitne dijelove za brojeve iz ovog izraza: 28 i 125;
2. Njihov proizvod: 28 125 = 3500;
3. U prvom množitelju decimalna točka se pomiče za 2 znamenke udesno (0,28 → 28), au drugom - za još jednu znamenku. Ukupno je potreban pomak ulijevo za tri znamenke: 3500 → 3.500 = 3,5.

Sada se pozabavimo izrazom 6.3 1.08.

1. Napišimo bitne dijelove: 63 i 108;
2. Njihov proizvod: 63 108 = 6804;
3. Opet, dva pomaka udesno: za 2 i 1 znamenku. Ukupno - opet 3 znamenke udesno, tako da će obrnuti pomak biti 3 znamenke ulijevo: 6804 → 6.804. Ovaj put na kraju nema nula.

Došli smo do trećeg izraza: 132,5 0,0034.

1. Značajniji dijelovi: 1325. i 34.;
2. Njihov proizvod: 1325 34 = 45 050;
3. U prvom razlomku decimalna točka ide udesno za 1 znamenku, a u drugom - za čak 4. Ukupno: 5 udesno. Izvodimo pomak za 5 ulijevo: 45050 → .45050 = 0,4505. Nula je uklonjena na kraju i dodana na prednju stranu kako ne bi ostala "gola" decimalna točka.

Sljedeći izraz: 0,0108 1600,5.

1. Pišemo značajne dijelove: 108 i 16 005;
2. Množimo ih: 108 16 005 = 1 728 540;
3. Brojimo brojeve iza decimalne točke: u prvom broju ima 4, u drugom - 1. Ukupno - opet 5. Imamo: 1.728.540 → 17.28540 = 17.2854. Na kraju je uklonjena "dodatna" nula.

Konačno, posljednji izraz: 5,25 10.000.

1. Značajni dijelovi: 525 i 1;
2. Množimo ih: 525 1 = 525;
3. Prvi razlomak je pomaknut 2 znamenke udesno, a drugi razlomak je pomaknut 4 znamenke ulijevo (10.000 → 1.0000 = 1). Ukupno 4 − 2 = 2 znamenke lijevo. Izvodimo obrnuti pomak za 2 znamenke udesno: 525, → 52 500 (morali smo dodati nule).

Obratite pažnju na posljednji primjer: budući da je decimalna točka pomaknuta na različitim smjerovima, ukupni pomak se nalazi kroz razliku. Ovo je jako važna točka! Evo još jednog primjera:

Razmotrimo brojeve 1,5 i 12 500. Imamo: 1,5 → 15 (pomak za 1 udesno); 12 500 → 125 (pomak 2 ulijevo). "Koramo" 1 znamenku udesno, a zatim 2 znamenke ulijevo. Kao rezultat toga, zakoračili smo 2 − 1 = 1 znamenku ulijevo.

Decimalna podjela

Podjela je možda i najviše složena operacija. Naravno, ovdje možete djelovati po analogiji s množenjem: podijeliti značajne dijelove, a zatim "premjestiti" decimalni zarez. Ali u ovom slučaju postoje mnoge suptilnosti koje negiraju potencijalnu uštedu.

Pogledajmo generički algoritam koji je malo duži, ali puno pouzdaniji:

1. Pretvorite sve decimale u obične razlomke. Uz malo vježbe, ovaj će vam korak oduzeti nekoliko sekundi;
2. Podijelite dobivene frakcije na klasičan način. Drugim riječima, pomnožite prvi razlomak s "obrnutim" drugim (pogledajte lekciju "Množenje i dijeljenje brojčanih razlomaka");
3. Ako je moguće, vratite rezultat kao decimalu. Ovaj korak je također brz, jer često nazivnik već ima stepen deset.

Zadatak. Pronađite vrijednost izraza:

1. 3,51: 3,9;
2. 1,47: 2,1;
3. 6,4: 25,6:
4. 0,0425: 2,5;
5. 0,25: 0,002.

Razmatramo prvi izraz. Prvo, pretvorimo obi razlomke u decimale:

Isto radimo i s drugim izrazom. Brojnik prvog razlomka ponovno se razlaže na faktore:

U trećem i četvrtom primjeru postoji važna točka: nakon što se riješite decimalnog zapisa, pojavljuju se razlomci koji se mogu poništiti. Međutim, nećemo izvršiti ovo smanjenje.

Posljednji primjer je zanimljiv jer je brojnik drugog razlomka prost broj. Ovdje jednostavno nema ništa za faktoriziranje, pa ga smatramo "praznim":

Ponekad dijeljenje rezultira cijelim brojem (govorim o posljednjem primjeru). U ovom slučaju, treći korak se uopće ne izvodi.

Osim toga, prilikom dijeljenja često se pojavljuju "ružni" razlomci koji se ne mogu pretvoriti u decimale. Po tome se dijeljenje razlikuje od množenja, gdje se rezultati uvijek izražavaju u decimalnom obliku. Naravno, u ovom slučaju, posljednji korak se opet ne izvodi.

Obratite pažnju i na 3. i 4. primjer. U njima namjerno ne reduciramo obične razlomke dobivene iz decimala. U suprotnom, to će zakomplicirati inverzni problem - predstavljanje konačnog odgovora ponovno u decimalnom obliku.

Zapamtite: osnovno svojstvo razlomka (kao i bilo koje drugo pravilo u matematici) samo po sebi ne znači da se mora primjenjivati ​​svugdje i uvijek, u svakoj prilici.