Progresija aritma. Zbroj aritmetičke progresije

Aritmetička progresija. Detaljna teorija s primjerima (2019.)

Numerički niz

Pa sjednimo i počnimo pisati neke brojeve. Na primjer:
Možete napisati bilo koje brojeve, a može ih biti koliko god želite (u našem slučaju, njih). Koliko god brojeva zapisali, uvijek možemo reći koji je od njih prvi, koji drugi i tako do posljednjeg, odnosno možemo ih numerirati. Ovo je primjer niza brojeva:

Numerički niz
Na primjer, za naš slijed:

Dodijeljeni broj je specifičan samo za jedan redni broj. Drugim riječima, u nizu ne postoje tri sekundarna broja. Drugi broj (kao i -ti broj) je uvijek isti.
Broj s brojem naziva se -ti član niza.

Cijeli niz obično nazivamo nekim slovom (npr.), a svaki član tog niza - istim slovom s indeksom jednakim broju ovog člana: .

u našem slučaju:

Recimo da imamo numerički niz u kojem je razlika između susjednih brojeva ista i jednaka.
Na primjer:

itd.
Takav brojčani niz naziva se aritmetička progresija.
Pojam "progresija" uveo je rimski autor Boecije još u 6. stoljeću i shvaćao ga se u širem smislu kao beskrajni brojčani niz. Naziv "aritmetika" prenio je iz teorije kontinuiranih proporcija, kojom su se bavili stari Grci.

Ovo je numerički niz, čiji je svaki član jednak prethodnom, zbrojen istim brojem. Taj se broj naziva razlika aritmetičke progresije i označava se.

Pokušajte odrediti koji nizovi brojeva su aritmetička progresija, a koji nisu:

a)
b)
c)
d)

Shvaćam? Usporedite naše odgovore:
Je aritmetička progresija - b, c.
Nije aritmetička progresija - a, d.

Vratimo se na zadanu progresiju () i pokušajmo pronaći vrijednost njezinog th člana. Postoji dva način da ga pronađete.

1. Metoda

Možemo dodati prethodnu vrijednost broja progresije sve dok ne dođemo do th člana progresije. Dobro je da nemamo puno za rezimirati - samo tri vrijednosti:

Dakle, -ti član opisane aritmetičke progresije jednak je.

2. Metoda

Što ako bismo trebali pronaći vrijednost th člana progresije? Zbrajanje bi nam oduzelo više od jednog sata, a nije činjenica da ne bismo pogriješili pri zbrajanju brojeva.
Naravno, matematičari su smislili način na koji ne morate prethodnoj vrijednosti dodati razliku aritmetičke progresije. Pažljivo pogledajte nacrtanu sliku ... Sigurno ste već primijetili određeni uzorak, i to:

Na primjer, pogledajmo što čini vrijednost --og člana ove aritmetičke progresije:

Drugim riječima:

Pokušajte na ovaj način samostalno pronaći vrijednost člana ove aritmetičke progresije.

Izračunati? Usporedite svoje unose s odgovorom:

Obratite pažnju da ste dobili potpuno isti broj kao u prethodnoj metodi, kada smo prethodnoj vrijednosti sukcesivno dodavali članove aritmetičke progresije.
Pokušajmo "depersonalizirati" ovu formulu - uvedimo je opći oblik i dobiti:

Jednadžba aritmetičke progresije.

Aritmetičke progresije se ili povećavaju ili smanjuju.

Povećanje- progresije u kojima je svaka sljedeća vrijednost pojmova veća od prethodne.
Na primjer:

Silazni- progresije u kojima je svaka sljedeća vrijednost pojmova manja od prethodne.
Na primjer:

Izvedena formula se koristi u izračunu izraza u rastućim i opadajućim izrazima aritmetičke progresije.
Provjerimo to u praksi.
Dano nam je aritmetička progresija, koji se sastoji od sljedećih brojeva: Provjerimo kakav će --ti broj ove aritmetičke progresije ispasti ako upotrijebimo našu formulu pri izračunu:

Od tad:

Tako smo se uvjerili da formula radi i u opadajućoj i u rastućoj aritmetičkoj progresiji.
Pokušajte sami pronaći -ti i -ti član ove aritmetičke progresije.

Usporedimo rezultate:

Svojstvo aritmetičke progresije

Zakomplicirajmo zadatak – izvodimo svojstvo aritmetičke progresije.
Pretpostavimo da nam je zadan sljedeći uvjet:
- aritmetička progresija, pronađite vrijednost.
Lako je, kažete, i počnite računati prema formuli koju već znate:

Neka, a, onda:

Apsolutno u pravu. Ispada da prvo pronađemo, a zatim ga dodamo prvom broju i dobijemo ono što tražimo. Ako je progresija predstavljena malim vrijednostima, onda u tome nema ništa komplicirano, ali što ako su nam dati brojevi u uvjetu? Slažem se, postoji mogućnost pogreške u izračunima.
Sada razmislite, je li moguće riješiti ovaj problem u jednom koraku pomoću bilo koje formule? Naravno, da, i sada ćemo to pokušati iznijeti.

Označimo željeni član aritmetičke progresije kao, znamo formulu za njegovo pronalaženje - to je ista formula koju smo izveli na početku:
, zatim:

prethodni član progresije je:
sljedeći termin progresije je:

Zbrojimo prethodne i sljedeće članove progresije:

Ispada da je zbroj prethodnog i sljedećih članova progresije dvostruko veći od vrijednosti člana progresije koji se nalazi između njih. Drugim riječima, da bismo pronašli vrijednost progresijskog člana s poznatim prethodnim i uzastopnim vrijednostima, potrebno ih je zbrojiti i podijeliti s.

Tako je, imamo isti broj. Popravimo materijal. Sami izračunajte vrijednost za napredovanje, jer to uopće nije teško.

Dobro napravljeno! Znate gotovo sve o napredovanju! Ostaje saznati samo jednu formulu koju je, prema legendi, jedan od najvećih matematičara svih vremena, "kralj matematičara" - Karl Gauss, lako zaključio za sebe...

Kada je Carl Gauss imao 9 godina, učitelj je, zauzet provjeravanjem rada učenika u drugim razredima, na satu zadao sljedeći zadatak: „Izračunaj zbroj svih prirodni brojevi od do (prema drugim izvorima do) uključivo. Kakvo je bilo iznenađenje učitelja kada je jedan od njegovih učenika (bio je to Karl Gauss) nakon minute dao točan odgovor na zadatak, dok je većina kolega iz razreda drznika nakon dugih proračuna dobila pogrešan rezultat ...

Mladi Carl Gauss primijetio je uzorak koji možete lako primijetiti.
Recimo da imamo aritmetičku progresiju koja se sastoji od -ti članova: Trebamo pronaći zbroj zadanih članova aritmetičke progresije. Naravno, možemo ručno zbrojiti sve vrijednosti, ali što ako trebamo pronaći zbroj njegovih članova u zadatku, kao što je Gauss tražio?

Opišimo napredovanje koje nam je dano. Promotrite pomno istaknute brojeve i pokušajte s njima izvesti razne matematičke operacije.

Pokušao? Što ste primijetili? Ispravno! Njihovi su iznosi jednaki

Sada odgovori, koliko će takvih parova biti u progresiji koja nam je dana? Naravno, točno polovica svih brojeva, tj.
Na temelju činjenice da je zbroj dvaju članova aritmetičke progresije jednak, i sličnih jednakih parova, dobivamo da ukupan iznos jednako je:
.
Dakle, formula za zbroj prvih članova bilo koje aritmetičke progresije bit će:

U nekim problemima ne znamo th pojam, ali znamo razliku u progresiji. Pokušajte zamijeniti formulu zbroja, formulu th člana.
Što si dobio?

Dobro napravljeno! Vratimo se sada na problem koji je zadan Carlu Gaussu: izračunajte sami koliki je zbroj brojeva koji počinju od -tog, a zbroj brojeva koji počinju od -tog.

Koliko ste dobili?
Gauss se pokazao da je zbroj članova jednak i zbroj članova. Jeste li tako odlučili?

Zapravo, formulu za zbroj članova aritmetičke progresije dokazao je starogrčki znanstvenik Diofant još u 3. stoljeću, a kroz to vrijeme duhoviti su ljudi silovito koristili svojstva aritmetičke progresije.
Na primjer, zamislite Stari Egipat i najveće gradilište tog vremena - izgradnju piramide... Slika prikazuje jednu njegovu stranu.

Kažete gdje je tu napredak? Pažljivo pogledajte i pronađite uzorak u broju pješčanih blokova u svakom redu zida piramide.

Zašto ne aritmetička progresija? Izračunajte koliko je blokova potrebno za izgradnju jednog zida ako su blok opeke postavljene u bazu. Nadam se da nećete brojati pomicanjem prsta po monitoru, sjećate li se zadnje formule i svega što smo rekli o aritmetičkoj progresiji?

NA ovaj slučaj napredovanje izgleda ovako:
Razlika aritmetičke progresije.
Broj članova aritmetičke progresije.
Zamijenimo naše podatke u posljednje formule (brojimo blokove na 2 načina).

Metoda 1.

Metoda 2.

A sada možete izračunati i na monitoru: usporedite dobivene vrijednosti s brojem blokova koji se nalaze u našoj piramidi. Je li se složilo? Bravo, savladali ste zbroj th članova aritmetičke progresije.
Naravno, ne možete izgraditi piramidu od blokova u podnožju, ali od? Pokušajte izračunati koliko je pješčanih opeka potrebno za izgradnju zida s ovim uvjetom.
Jeste li uspjeli?
Točan odgovor su blokovi:

Vježbati

Zadaci:

Maša je u formi za ljeto. Svakim danom povećava broj čučnjeva. Koliko će puta Maša čučnuti u tjednima ako je napravila čučnjeve na prvom treningu.
Koliki je zbroj svih neparnih brojeva sadržanih u.
Prilikom skladištenja trupaca, drvosječe ih slažu na način da svaki gornji sloj sadrži jedan dnevnik manje od prethodnog. Koliko je trupaca u jednom zidu, ako je baza zidanja trupci.

odgovori:

Definirajmo parametre aritmetičke progresije. U ovom slučaju
(tjedni = dani).
Odgovor: Za dva tjedna Maša bi trebala čučnuti jednom dnevno.
Prvi neparni broj, zadnji broj.
Razlika aritmetičke progresije.
Broj neparnih brojeva na pola, međutim, provjerite ovu činjenicu koristeći formulu za pronalaženje -tog člana aritmetičke progresije:
Brojevi sadrže neparne brojeve.
Dostupne podatke zamjenjujemo u formulu:
Odgovor: Zbroj svih neparnih brojeva sadržanih u jednak je.
Prisjetite se problema s piramidama. U našem slučaju, a, budući da je svaki gornji sloj smanjen za jedan dnevnik, postoji samo hrpa slojeva, tj.
Zamijenite podatke u formuli:
Odgovor: U zidanju su trupci.

Sumirati

- numerički niz u kojem je razlika između susjednih brojeva jednaka i jednaka. Povećava se i smanjuje.
Pronalaženje formule. član aritmetičke progresije zapisuje se formulom - , gdje je broj brojeva u progresiji.
Svojstvo članova aritmetičke progresije- - gdje - broj brojeva u progresiji.
Zbroj članova aritmetičke progresije može se pronaći na dva načina:

, gdje je broj vrijednosti.

ARITHMETIČKI NAPREDAK. PROSJEČNA RAZINA

Numerički niz

Sjednimo i počnemo pisati neke brojeve. Na primjer:

Možete napisati bilo koje brojeve, a može ih biti koliko god želite. Ali uvijek možete reći tko je od njih prvi, koji je drugi i tako dalje, odnosno možemo ih pobrojati. Ovo je primjer niza brojeva.

Numerički niz je skup brojeva, od kojih se svakom može dodijeliti jedinstveni broj.

Drugim riječima, svaki se broj može povezati s određenim prirodnim brojem, i to samo s jednim. I nećemo dodijeliti ovaj broj nijednom drugom broju iz ovog skupa.

Broj s brojem naziva se -ti član niza.

Cijeli niz obično nazivamo nekim slovom (npr.), a svaki član tog niza - istim slovom s indeksom jednakim broju ovog člana: .

Vrlo je zgodno ako se --ti član niza može dati nekom formulom. Na primjer, formula

postavlja slijed:

A formula je sljedeći niz:

Na primjer, aritmetička progresija je niz (prvi član ovdje je jednak, a razlika). Ili (, razlika).

n-ti izraz formula

Rekurentnom nazivamo formulu u kojoj, da biste saznali --ti pojam, morate znati prethodni ili nekoliko prethodnih:

Da bismo pronašli, na primjer, th član progresije pomoću takve formule, moramo izračunati prethodnih devet. Na primjer, neka. Zatim:

E, sad je jasno koja je formula?

U svakom retku zbrajamo do, pomnoženo s nekim brojem. Za što? Vrlo jednostavno: ovo je broj trenutnog člana minus:

Sada je mnogo udobnije, zar ne? Provjeravamo:

Odlučite sami:

U aritmetičkoj progresiji pronađite formulu za n-ti član i pronađite stoti član.

Riješenje:

Prvi član je jednak. A koja je razlika? A evo što:

(uostalom, naziva se razlika jer je jednaka razlici uzastopnih članova progresije).

Dakle, formula je:

Tada je stoti član:

Koliki je zbroj svih prirodnih brojeva od do?

Prema legendi, veliki matematičar Carl Gauss, kao 9-godišnji dječak, izračunao je ovaj iznos za nekoliko minuta. Uočio je da je zbroj prvog i zadnjeg broja jednak, zbroj drugog i pretposljednjeg jednak, zbroj trećeg i trećeg s kraja isti, i tako dalje. Koliko ima takvih parova? Tako je, točno pola broja svih brojeva, tj. Tako,

Opća formula za zbroj prvih članova bilo koje aritmetičke progresije bit će:

Primjer:
Pronađite zbroj svih dvoznamenkasti brojevi, višestruki.

Riješenje:

Prvi takav broj je ovaj. Svaki sljedeći dobiva se dodavanjem broja prethodnom. Dakle, brojevi koji nas zanimaju čine aritmetičku progresiju s prvim članom i razlikom.

Formula za th član za ovu progresiju je:

Koliko je članova u progresiji ako svi moraju biti dvoznamenkasti?

Vrlo jednostavno: .

Posljednji član progresije bit će jednak. Zatim zbroj:

Odgovor: .

Sada odlučite sami:

Svaki dan sportaš trči 1m više nego prethodnog dana. Koliko će kilometara pretrčati u tjednima ako je prvi dan pretrčao km m?
Biciklist svaki dan prijeđe više kilometara od prethodnog. Prvog dana putovao je km. Koliko dana mora voziti da prijeđe kilometar? Koliko će kilometara prijeći posljednjeg dana putovanja?
Cijena hladnjaka u trgovini svake se godine smanjuje za isti iznos. Odredite za koliko se cijena hladnjaka smanjivala svake godine ako je, stavljen na prodaju za rublje, šest godina kasnije prodan za rublje.

odgovori:

Ovdje je najvažnije prepoznati aritmetičku progresiju i odrediti njezine parametre. U ovom slučaju, (tjedni = dani). Morate odrediti zbroj prvih članova ove progresije:
.
Odgovor:
Ovdje je dano:, potrebno je pronaći.
Očito, morate koristiti istu formulu zbroja kao u prethodnom problemu:
.
Zamijenite vrijednosti:
Korijen očito ne odgovara, pa odgovor.
Izračunajmo prijeđenu udaljenost tijekom posljednjeg dana koristeći formulu --og člana:
(km).
Odgovor:
S obzirom na: . Pronaći: .
Ne postaje lakše:
(trljati).
Odgovor:

ARITHMETIČKI NAPREDAK. UKRATKO O GLAVNOM

Ovo je numerički niz u kojem je razlika između susjednih brojeva ista i jednaka.

Aritmetička progresija raste () i opada ().

Na primjer:

Formula za pronalaženje n-tog člana aritmetičke progresije

zapisuje se kao formula, gdje je broj brojeva u progresiji.

Svojstvo članova aritmetičke progresije

Olakšava pronalaženje člana progresije ako su poznati njegovi susjedni članovi - gdje je broj brojeva u progresiji.

Zbroj članova aritmetičke progresije

Postoje dva načina za pronalaženje zbroja:

Gdje je broj vrijednosti.

Problemi aritmetičke progresije postoje od davnina. Pojavili su se i tražili rješenje, jer su imali praktičnu potrebu.

Dakle, u jednom od papirusa drevni Egipt, koji ima matematički sadržaj - Rhindov papirus (XIX st. pr. Kr.) - sadrži sljedeći zadatak: deset mjera kruha podijeliti na deset osoba, s tim da je razlika između svake od njih jedna osmina mjere.

A u matematičkim djelima starih Grka postoje elegantni teoremi vezani uz aritmetičku progresiju. Dakle, Hipsikle iz Aleksandrije (2. stoljeće, koji je sastavio mnoge zanimljive probleme i dodao četrnaestu knjigu Euklidovim "Elementima"), formulirao je ideju: "U aritmetičkoj progresiji s parnim brojem članova, zbroj članova 2. pol. veći je od zbroja članova 1. za kvadrat 1/2 članova.

Niz an je označen. Brojevi niza nazivaju se njegovim članovima i obično se označavaju slovima s indeksima koji označavaju serijski broj tog člana (a1, a2, a3 ... on glasi: "a 1st", "a 2nd", "a 3rd ” i tako dalje).

Niz može biti beskonačan ili konačan.

Što je aritmetička progresija? Podrazumijeva se kao dobiveno zbrajanjem prethodnog člana (n) s istim brojem d, što je razlika progresije.

Ako d<0, то мы имеем убывающую прогрессию. Если d>0, onda se smatra da se takva progresija povećava.

Za aritmetičku progresiju kaže se da je konačna ako se uzme u obzir samo nekoliko njezinih prvih članova. Na vrlo u velikom brojučlanovi su već beskonačna progresija.

Svaka aritmetička progresija dana je sljedećom formulom:

an =kn+b, dok su b i k neki brojevi.

Izjava, koja je suprotna, apsolutno je istinita: ako je niz zadan sličnom formulom, onda je to upravo aritmetička progresija koja ima svojstva:

Svaki član progresije je aritmetička sredina prethodnog i sljedećeg člana.
Suprotno: ako je, počevši od 2., svaki član aritmetička sredina prethodnog člana i sljedećeg, t.j. ako je uvjet ispunjen, tada je zadani niz aritmetička progresija. Ova jednakost je također znak progresije, pa se obično naziva karakterističnim svojstvom progresije.
Na isti način, teorem koji odražava ovo svojstvo je istinit: niz je aritmetička progresija samo ako je ta jednakost istinita za bilo koji od članova niza, počevši od 2.

Karakteristično svojstvo za bilo koja četiri broja aritmetičke progresije može se izraziti formulom an + am = ak + al ako je n + m = k + l (m, n, k su brojevi progresije).

U aritmetičkoj progresiji, bilo koji nužni (N-ti) član može se pronaći primjenom sljedeće formule:

Na primjer: prvi član (a1) u aritmetičkoj progresiji je zadan i jednak je tri, a razlika (d) jednaka je četiri. Morate pronaći četrdeset peti član ove progresije. a45 = 1+4(45-1)=177

Formula an = ak + d(n - k) omogućuje nam da odredimo n-ti član aritmetičku progresiju kroz bilo koji njegov k-ti član, pod uvjetom da je poznat.

Zbroj članova aritmetičke progresije (uz pretpostavku 1. n članova konačna progresija) izračunava se na sljedeći način:

Sn = (a1+an) n/2.

Ako je i 1. član poznat, onda je druga formula prikladna za izračun:

Sn = ((2a1+d(n-1))/2)*n.

Zbroj aritmetičke progresije koja sadrži n članova izračunava se na sljedeći način:

Izbor formula za izračune ovisi o uvjetima zadataka i početnim podacima.

Prirodni nizovi bilo kojih brojeva kao što su 1,2,3,...,n,...- najjednostavniji primjer aritmetička progresija.

Osim aritmetičke progresije, postoji i geometrijska, koja ima svoja svojstva i karakteristike.

Mnogi su čuli za aritmetičku progresiju, ali nisu svi dobro svjesni što je to. U ovom članku dat ćemo odgovarajuću definiciju, a također ćemo razmotriti pitanje kako pronaći razliku aritmetičke progresije i dati niz primjera.

Matematička definicija

Dakle, ako govorimo o aritmetičkoj ili algebarskoj progresiji (ovi koncepti definiraju istu stvar), onda to znači da postoji neka brojevni niz zadovoljavajući sljedeći zakon: svaka dva susjedna broja u nizu razlikuju se za isti iznos. Matematički, ovo se piše ovako:

Ovdje n znači broj elementa a n u nizu, a broj d je razlika progresije (njegov naziv proizlazi iz prikazane formule).

Što znači znati razliku d? O tome koliko su međusobno udaljeni susjedni brojevi. Međutim, poznavanje d je nužan, ali ne i dovoljan uvjet za određivanje (obnavljanje) cjelokupne progresije. Morate znati još jedan broj, koji može biti apsolutno bilo koji element niza koji se razmatra, na primjer, 4, a10, ali u pravilu se koristi prvi broj, odnosno 1.

Formule za određivanje elemenata progresije

Općenito, gore navedene informacije već su dovoljne za prelazak na rješavanje konkretnih problema. Ipak, prije nego što se zada aritmetička progresija, a bit će potrebno pronaći njezinu razliku, predstavljamo nekoliko korisnih formula, čime ćemo olakšati daljnji proces rješavanja problema.

Lako je pokazati da se bilo koji element niza s brojem n može pronaći na sljedeći način:

a n \u003d a 1 + (n - 1) * d

Doista, svatko može provjeriti ovu formulu jednostavnim nabrajanjem: ako zamijenite n = 1, tada ćete dobiti prvi element, ako zamijenite n = 2, tada izraz daje zbroj prvog broja i razlike, i tako dalje .

Uvjeti mnogih zadataka sastavljeni su na način da je za poznati par brojeva, čiji su brojevi također dati u nizu, potrebno obnoviti cijeli niz brojeva (naći razliku i prvi element). Sada ćemo ovaj problem riješiti na opći način.

Dakle, recimo da su nam dana dva elementa s brojevima n i m. Koristeći gornju formulu, možemo sastaviti sustav od dvije jednadžbe:

a n \u003d a 1 + (n - 1) * d;
a m = a 1 + (m - 1) * d

Za pronalaženje nepoznatih veličina koristimo se poznatom jednostavnom metodom rješavanja takvog sustava: lijevi i desni dio oduzimamo u paru, a jednakost ostaje važeća. Imamo:

a n \u003d a 1 + (n - 1) * d;
a n - a m = (n - 1) * d - (m - 1) * d = d * (n - m)

Tako smo eliminirali jednu nepoznatu (a 1). Sada možemo napisati konačni izraz za određivanje d:

d = (a n - a m) / (n - m), gdje je n > m

Dobili smo vrlo jednostavnu formulu: da bismo izračunali razliku d u skladu s uvjetima zadatka, potrebno je samo uzeti omjer razlika između samih elemenata i njihovih serijskih brojeva. Treba se usredotočiti na jedno važna točka Napomena: razlike se uzimaju između "viših" i "nižih" članova, odnosno n > m ("viši" znači da stoji dalje od početka niza, njegova apsolutna vrijednost može biti ili veća ili manja od "mlađeg" "element).

Izraz za razliku d progresije treba zamijeniti u bilo koju od jednadžbi na početku rješenja zadatka kako bi se dobila vrijednost prvog člana.

U naše doba razvoja računalne tehnologije mnogi školarci pokušavaju pronaći rješenja za svoje zadatke na internetu, pa se često postavljaju pitanja ovog tipa: pronaći razliku aritmetičke progresije na internetu. Na takav zahtjev tražilica će prikazati niz web stranica, odlaskom na koje ćete morati unijeti podatke poznate iz uvjeta (mogu biti dva člana progresije ili zbroj nekih od njih) i odmah dobiti odgovor. Ipak, takav pristup rješavanju problema je neproduktivan u smislu razvoja učenika i razumijevanja suštine zadatka koji mu je dodijeljen.

Rješenje bez korištenja formula

Riješimo prvi problem, pri čemu nećemo koristiti nijednu od navedenih formula. Neka su zadani elementi niza: a6 = 3, a9 = 18. Nađi razliku aritmetičke progresije.

Poznati elementi su blizu jedan drugom u nizu. Koliko se puta razlika d treba dodati najmanjoj da bi se dobila najveća? Tri puta (prvi put dodavanjem d, dobivamo 7. element, drugi put - osmi, konačno, treći put - deveti). Koji broj tri puta treba dodati tri da dobijemo 18? Ovo je broj pet. Stvarno:

Dakle, nepoznata razlika je d = 5.

Naravno, rješenje se moglo napraviti odgovarajućom formulom, ali to nije učinjeno namjerno. Detaljno objašnjenje rješenja problema trebalo bi postati jasan i živopisan primjer što je aritmetička progresija.

Zadatak sličan prethodnom

Sada riješimo sličan problem, ali promijenimo ulazne podatke. Dakle, trebali biste pronaći ako je a3 = 2, a9 = 19.

Naravno, možete ponovno posegnuti za metodom rješavanja "na čelo". Ali budući da su dati elementi serije, koji su relativno udaljeni, takva metoda postaje ne baš prikladna. Ali korištenje rezultirajuće formule brzo će nas dovesti do odgovora:

d \u003d (a 9 - a 3) / (9 - 3) \u003d (19 - 2) / (6) \u003d 17 / 6 ≈ 2,83

Ovdje smo zaokružili konačan broj. Koliko je ovo zaokruživanje dovelo do greške može se procijeniti provjerom rezultata:

a 9 \u003d a 3 + 2,83 + 2,83 + 2,83 + 2,83 + 2,83 + 2,83 \u003d 18,98

Ovaj rezultat razlikuje se za samo 0,1% od vrijednosti navedene u uvjetu. Stoga se zaokruživanje na stotinke može smatrati dobrim izborom.

Zadaci za primjenu formule za člana

Smatrati klasičan primjer zadaci za određivanje nepoznate d: nađi razliku aritmetičke progresije ako je a1 = 12, a5 = 40.

Kada se zadaju dva broja nepoznatog algebarskog niza, a jedan od njih je element a 1 , tada ne trebate dugo razmišljati, već odmah primijeniti formulu za a n član. U ovom slučaju imamo:

a 5 = a 1 + d * (5 - 1) => d = (a 5 - a 1) / 4 = (40 - 12) / 4 = 7

Točan broj smo dobili prilikom dijeljenja, pa nema smisla provjeravati točnost izračunatog rezultata, kao što je to učinjeno u prethodnom stavku.

Riješimo još jedan sličan problem: trebali bismo pronaći razliku aritmetičke progresije ako je a1 = 16, a8 = 37.

Koristimo sličan pristup prethodnom i dobivamo:

a 8 = a 1 + d * (8 - 1) => d = (a 8 - a 1) / 7 = (37 - 16) / 7 = 3

Što još trebate znati o aritmetičkoj progresiji

Osim zadataka pronalaženja nepoznate razlike odn pojedinačni elementi, često je potrebno riješiti probleme zbroja prvih članova niza. Razmatranje ovih problema je izvan okvira teme članka, međutim, radi cjelovitosti informacija, donosimo opću formulu za zbroj n brojeva niza:

∑ n i = 1 (a i) = n * (a 1 + a n) / 2

Zbroj aritmetičke progresije.

Zbroj aritmetičke progresije je jednostavna stvar. I po značenju i po formuli. Ali na ovu temu ima svakakvih zadataka. Od osnovnog do sasvim solidnog.

Prvo, pozabavimo se značenjem i formulom zbroja. A onda ćemo odlučiti. Za vlastito zadovoljstvo.) Značenje zbroja je jednostavno kao nišanje. Da biste pronašli zbroj aritmetičke progresije, samo trebate pažljivo zbrojiti sve njegove članove. Ako je ovih pojmova malo, možete ih dodati bez ikakvih formula. Ali ako ima puno, ili puno ... dodatak je neugodan.) U ovom slučaju formula štedi.

Formula sume je jednostavna:

Idemo shvatiti kakva su slova uključena u formulu. Ovo će razjasniti mnogo toga.

S n je zbroj aritmetičke progresije. Rezultat zbrajanja svičlanovi, s prvi na posljednji. To je važno. Točno zbrojite svičlanovi u nizu, bez razmaka i skokova. I, točno, počevši od prvi. U problemima poput pronalaženja zbroja trećeg i osmog člana ili zbroja članova od petog do dvadesetog, izravna primjena formule bit će razočaravajuća.)

a 1 - prvičlan progresije. Ovdje je sve jasno, jednostavno prvi broj reda.

a n- posljednjičlan progresije. Zadnji broj retka. Nije baš poznato ime, ali, kada se primjenjuje na količinu, vrlo je prikladno. Tada ćete se i sami uvjeriti.

n je broj posljednjeg člana. Važno je razumjeti da je u formuli ovaj broj poklapa se s brojem dodanih pojmova.

Definirajmo pojam posljednjičlan a n. Popunjavajuće pitanje: kakav će član posljednji, ako se daje beskrajna aritmetička progresija?

Za pouzdan odgovor morate razumjeti osnovno značenje aritmetičke progresije i ... pažljivo pročitati zadatak!)

U zadatku pronalaženja zbroja aritmetičke progresije uvijek se pojavljuje zadnji član (izravno ili neizravno), koji bi trebao biti ograničen. Inače, konačan, specifičan iznos jednostavno ne postoji. Za rješenje nije važno kakva je progresija dana: konačna ili beskonačna. Nije važno kako je zadan: nizom brojeva ili formulom n-tog člana.

Najvažnije je razumjeti da formula funkcionira od prvog člana progresije do pojma s brojem n. Zapravo, puni naziv formule izgleda ovako: zbroj prvih n članova aritmetičke progresije. Broj ovih prvih članova, tj. n, određen je isključivo zadatkom. U zadatku sve ovo vrijedne informaciječesto šifrirano, da... Ali u redu je, u primjerima u nastavku otkrit ćemo ove tajne.)

Primjeri zadataka za zbroj aritmetičke progresije.

prvenstveno, korisna informacija:

Glavna poteškoća u zadacima za zbroj aritmetičke progresije je ispravno određivanje elemenata formule.

Autori zadataka šifriraju upravo te elemente bezgraničnom maštom.) Ovdje je glavna stvar ne bojati se. Razumijevajući bit elemenata, dovoljno ih je samo dešifrirati. Pogledajmo detaljno nekoliko primjera. Počnimo sa zadatkom na temelju pravog GIA.

1. Aritmetička progresija dana je uvjetom: a n = 2n-3,5. Pronađite zbroj prvih 10 članova.

Dobar posao. Lako.) Što trebamo znati da bismo odredili količinu prema formuli? Prvi član a 1, prošli mandat a n, da broj posljednjeg člana n.

Gdje dobiti zadnji broj člana n? Da, tamo, u stanju! Piše pronaći zbroj prvih 10 članova. Pa koji će to biti broj posljednji, deseti član?) Nećete vjerovati, njegov broj je deseti!) Stoga, umjesto a n zamijenit ćemo u formulu a 10, ali umjesto n- deset. Opet, broj posljednjeg člana je isti kao i broj članova.

Ostaje da se utvrdi a 1 i a 10. To se lako izračunava formulom n-tog člana, koja je dana u opisu problema. Ne znate kako to učiniti? Posjetite prethodnu lekciju, bez ovoga - ništa.

a 1= 2 1 - 3,5 = -1,5

a 10\u003d 2 10 - 3,5 \u003d 16,5

S n = S 10.

Saznali smo značenje svih elemenata formule za zbroj aritmetičke progresije. Ostaje ih zamijeniti i računati:

To je sve o tome. Odgovor: 75.

Još jedan zadatak baziran na GIA-i. Malo kompliciranije:

2. Zadana je aritmetička progresija (a n), čija je razlika 3,7; a 1 \u003d 2.3. Pronađite zbroj prvih 15 članova.

Odmah pišemo formulu zbroja:

Ova formula nam omogućuje da pronađemo vrijednost bilo kojeg člana po njegovom broju. Tražimo jednostavnu zamjenu:

a 15 \u003d 2,3 + (15-1) 3,7 \u003d 54,1

Ostaje zamijeniti sve elemente u formuli za zbroj aritmetičke progresije i izračunati odgovor:

Odgovor: 423.

Usput, ako u formuli zbroja umjesto a n samo zamijenimo formulu n-tog člana, dobivamo:

Dajemo slične, dobivamo novu formulu za zbroj članova aritmetičke progresije:

Kao što vidite, n-ti pojam ovdje nije potreban. a n. U nekim zadacima ova formula jako pomaže, da... Možete zapamtiti ovu formulu. A možete ga jednostavno povući u pravo vrijeme, kao ovdje. Uostalom, formula za zbroj i formula za n-ti član moraju se pamtiti na svaki način.)

Sada zadatak u obliku kratke enkripcije):

3. Pronađite zbroj svih pozitivnih dvoznamenkastih brojeva koji su višekratnici tri.

Kako! Nema prvog člana, nema posljednjeg, uopće nema napredovanja... Kako živjeti!?

Morat ćete razmišljati svojom glavom i iz uvjeta izvući sve elemente zbroja aritmetičke progresije. Što su dvoznamenkasti brojevi – znamo. Sastoje se od dva broja.) Koji će dvoznamenkasti broj prvi? 10, vjerojatno.) zadnja stvar dvoznamenkasti broj? 99, naravno! Trocifrene će ga slijediti...

Višekratnici tri... Hm... Ovo su brojevi koji su jednako djeljivi s tri, evo! Deset nije djeljivo s tri, 11 nije djeljivo... 12... je djeljivo! Dakle, nešto se pojavljuje. Već možete napisati niz prema stanju problema:

12, 15, 18, 21, ... 96, 99.

Hoće li ova serija biti aritmetička progresija? Naravno! Svaki pojam razlikuje se od prethodnog striktno za tri. Ako se pojmu doda 2, ili 4, recimo, rezultat, t.j. novi broj se više neće dijeliti s 3. Možete odmah odrediti razliku aritmetičke progresije do hrpe: d = 3. Koristan!)

Dakle, možemo sigurno zapisati neke parametre progresije:

Koji će biti broj n zadnji član? Tko misli da je 99 kobno se vara... Brojevi - uvijek idu redom, a naši članovi preskaču prva tri. Ne poklapaju se.

Ovdje postoje dva rješenja. Jedan od načina je za super vrijedne. Možete slikati progresiju, cijeli niz brojeva i prstom brojati broj pojmova.) Drugi način je za promišljene. Morate zapamtiti formulu za n-ti član. Ako se formula primijeni na naš problem, dobivamo da je 99 trideseti član progresije. Oni. n = 30.

Gledamo formulu za zbroj aritmetičke progresije:

Gledamo i radujemo se.) Sve što je potrebno za izračun iznosa izvukli smo iz stanja problema:

a 1= 12.

a 30= 99.

S n = S 30.

Ono što ostaje je elementarna aritmetika. Zamijenite brojeve u formuli i izračunajte:

Odgovor: 1665

Druga vrsta popularnih zagonetki:

4. Zadana je aritmetička progresija:

-21,5; -20; -18,5; -17; ...

Pronađite zbroj pojmova od dvadesetog do trideset četvrtog.

Gledamo formulu zbroja i ... uznemireni smo.) Formula, da vas podsjetim, izračunava zbroj od prvečlan. A u zadatku trebate izračunati zbroj od dvadesetog... Formula neće raditi.

Možete, naravno, slikati cijelu progresiju u nizu i staviti pojmove od 20 do 34. Ali ... nekako ispadne glupo i dugo, zar ne?)

Ima još elegantno rješenje. Podijelimo našu seriju na dva dijela. Prvi dio će od prvog mandata do devetnaestog. Drugi dio - dvadeset do trideset i četiri. Jasno je da ako izračunamo zbroj članova prvog dijela S 1-19, dodajmo je zbroju članova drugog dijela S 20-34, dobivamo zbroj progresije od prvog člana do trideset četvrtog S 1-34. Kao ovo:

S 1-19 + S 20-34 = S 1-34

Ovo pokazuje da se nalazi zbroj S 20-34 može se učiniti jednostavnim oduzimanjem

S 20-34 = S 1-34 - S 1-19

Uzimaju se u obzir oba zbroja na desnoj strani od prvečlan, tj. primjenjivo na njih standardna formula iznosi. Počinjemo li?

Izvlačimo parametre progresije iz uvjeta zadatka:

d = 1,5.

a 1= -21,5.

Da bismo izračunali zbroje prvih 19 i prva 34 člana, trebat će nam 19. i 34. član. Brojimo ih prema formuli n-tog člana, kao u zadatku 2:

a 19\u003d -21,5 + (19-1) 1,5 \u003d 5,5

a 34\u003d -21,5 + (34-1) 1,5 \u003d 28

Ništa više nije ostalo. Od zbroja 34 člana oduzmite zbroj 19 članova:

S 20-34 = S 1-34 - S 1-19 = 110,5 - (-152) = 262,5

Odgovor: 262,5

Jedan važna nota! Postoji vrlo korisna značajka u rješavanju ovog problema. Umjesto izravnog izračuna što trebate (S 20-34), brojali smo što, čini se, nije potrebno - S 1-19. A onda su odredili S 20-34, odbacujući nepotrebno iz punog rezultata. Takva "finta s ušima" često spašava u zlim zagonetkama.)

U ovoj lekciji razmatrali smo probleme za čije je rješavanje dovoljno razumjeti značenje zbroja aritmetičke progresije. Pa, morate znati nekoliko formula.)

praktični savjeti:

Prilikom rješavanja bilo kojeg problema za zbroj aritmetičke progresije, preporučam da odmah napišete dvije glavne formule iz ove teme.

Formula n-tog člana:

Ove formule će vam odmah reći što tražiti, u kojem smjeru razmišljati kako biste riješili problem. Pomaže.

A sada zadaci za samostalno rješavanje.

5. Pronađite zbroj svih dvoznamenkastih brojeva koji nisu djeljivi s tri.

Cool?) Nagovještaj je skriven u bilješci uz problem 4. Pa, problem 3 će pomoći.

6. Aritmetička progresija dana je uvjetom: a 1 =-5,5; a n+1 = a n +0,5. Pronađite zbroj prva 24 člana.

Neobično?) Ovo je formula koja se ponavlja. O tome možete pročitati u prethodnoj lekciji. Nemojte zanemariti vezu, takve se zagonetke često nalaze u GIA-i.

7. Vasya je skupio novac za praznik. Čak 4550 rubalja! I odlučio sam najdražoj osobi (sebi) pokloniti nekoliko dana sreće). Živite lijepo ne uskraćujući sebi ništa. Potrošite 500 rubalja prvog dana, a svaki sljedeći dan potrošite 50 rubalja više nego prethodnog! Dok ne ponestane novca. Koliko je dana sreće imao Vasya?

Je li teško?) Dodatna formula iz zadatka 2 pomoći će.

Odgovori (u neredu): 7, 3240, 6.

Ako vam se sviđa ova stranica...

Usput, imam još nekoliko zanimljivih stranica za vas.)

Možete vježbati rješavanje primjera i saznati svoju razinu. Testiranje s trenutnom provjerom. Učenje - sa zanimanjem!)

možete se upoznati s funkcijama i izvedenicama.

Netko se s oprezom odnosi prema riječi "progresija", kao prema vrlo složenom pojmu iz odjeljaka više matematike. U međuvremenu, najjednostavnija aritmetička progresija je rad taksi brojača (gdje još uvijek ostaju). A razumjeti bit (a u matematici nema ništa važnije od "razumijevanja suštine") aritmetičkog niza nije tako teško, analizirajući nekoliko elementarnih pojmova.

Matematički niz brojeva

Uobičajeno je numerički niz nazivati nizom brojeva, od kojih svaki ima svoj broj.

i 1 je prvi član niza;

i 2 je drugi član niza;

i 7 je sedmi član niza;

i n je n-ti član niza;

Međutim, ne zanima nas bilo koji proizvoljan skup brojki i brojeva. Pozornost ćemo usmjeriti na numerički niz u kojem je vrijednost n-tog člana povezana s njegovim rednim brojem ovisnošću koja se može jasno matematički formulirati. Drugim riječima: brojčana vrijednost n-tog broja je neka funkcija od n.

a - vrijednost člana brojčanog niza;

n je njegov serijski broj;

f(n) je funkcija gdje je ordinal u numeričkom nizu n argument.

Definicija

Aritmetičkom progresijom obično se naziva numerički niz u kojem je svaki sljedeći član veći (manji) od prethodnog za isti broj. Formula za n-ti član aritmetičkog niza je sljedeća:

a n - vrijednost trenutnog člana aritmetičke progresije;

a n+1 - formula sljedećeg broja;

d - razlika (određeni broj).

Lako je utvrditi da ako je razlika pozitivna (d>0), tada će svaki sljedeći član razmatranog niza biti veći od prethodnog, te će se takva aritmetička progresija povećavati.

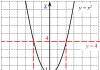
Na donjem grafikonu lako je vidjeti zašto se brojčani niz naziva "rastući".

U slučajevima kada je razlika negativna (d<0), каждый последующий член по понятным причинам будет меньше предыдущего, график прогрессии станет «уходить» вниз, арифметическая прогрессия, соответственно, будет именоваться убывающей.

Vrijednost navedenog člana

Ponekad je potrebno odrediti vrijednost nekog proizvoljnog člana a n aritmetičke progresije. To možete učiniti tako da uzastopno izračunate vrijednosti svih članova aritmetičke progresije, od prvog do željenog. Međutim, ovaj način nije uvijek prihvatljiv ako je, na primjer, potrebno pronaći vrijednost pettisućitog ili osmomilijuntnog člana. Tradicionalni izračun će potrajati dugo. Međutim, određena aritmetička progresija može se istražiti korištenjem određenih formula. Postoji i formula za n-ti član: vrijednost bilo kojeg člana aritmetičke progresije može se odrediti kao zbroj prvog člana progresije s razlikom progresije, pomnoženom s brojem željenog člana, minus jedan .

Formula je univerzalna za povećanje i smanjenje progresije.

Primjer izračunavanja vrijednosti zadanog člana

Riješimo sljedeći problem nalaženja vrijednosti n-tog člana aritmetičke progresije.

Uvjet: postoji aritmetička progresija s parametrima:

Prvi član niza je 3;

Razlika u nizu brojeva je 1,2.

Zadatak: potrebno je pronaći vrijednost 214 pojmova

Rješenje: za određivanje vrijednosti danog člana koristimo formulu:

a(n) = a1 + d(n-1)

Zamjenom podataka iz iskaza problema u izraz, imamo:

a(214) = a1 + d(n-1)

a(214) = 3 + 1,2 (214-1) = 258,6

Odgovor: 214. član niza jednak je 258,6.

Prednosti ove metode izračuna su očite - cijelo rješenje ne traje više od 2 retka.

Zbroj zadanog broja pojmova

Vrlo često, u danom aritmetičkom nizu, potrebno je odrediti zbroj vrijednosti nekih njegovih segmenata. Također ne treba izračunavati vrijednosti svakog pojma i zatim ih zbrajati. Ova metoda je primjenjiva ako je mali broj članova čiji se zbroj mora pronaći. U drugim slučajevima, prikladnije je koristiti sljedeću formulu.

Zbroj članova aritmetičke progresije od 1 do n jednak je zbroju prvog i n-tog člana, pomnoženog s brojem člana n i podijeljenog s dva. Ako se u formuli vrijednost n-tog člana zamijeni izrazom iz prethodnog stavka članka, dobivamo:

Primjer izračuna

Na primjer, riješimo problem sa sljedećim uvjetima:

Prvi član niza je nula;

Razlika je 0,5.

U zadatku je potrebno odrediti zbroj članova niza od 56 do 101.

Riješenje. Koristimo formulu za određivanje zbroja progresije:

s(n) = (2∙a1 + d∙(n-1))∙n/2

Prvo određujemo zbroj vrijednosti 101 člana progresije zamjenom zadanih uvjeta našeg problema u formulu:

s 101 = (2∙0 + 0,5∙(101-1))∙101/2 = 2 525

Očito, da bi se saznao zbroj uvjeta progresije od 56. do 101., potrebno je od S 101 oduzeti S 55.

s 55 = (2∙0 + 0,5∙(55-1))∙55/2 = 742,5

Dakle, zbroj aritmetičke progresije za ovaj primjer je:

s 101 - s 55 \u003d 2.525 - 742,5 \u003d 1.782,5

Primjer praktične primjene aritmetičke progresije

Na kraju članka vratimo se primjeru aritmetičkog niza danog u prvom odlomku – taksimetar (taxi autometar). Razmotrimo takav primjer.

Ulazak u taksi (koji uključuje 3 km) košta 50 rubalja. Svaki sljedeći kilometar plaća se po stopi od 22 rublja / km. Udaljenost putovanja 30 km. Izračunajte cijenu putovanja.

1. Odbacimo prva 3 km čija je cijena uključena u cijenu slijetanja.

30 - 3 = 27 km.

2. Daljnji izračun nije ništa drugo nego raščlanjivanje niza aritmetičkih brojeva.

Članski broj je broj prijeđenih kilometara (minus prva tri).

Vrijednost člana je zbroj.

Prvi termin u ovom problemu bit će jednak 1 = 50 rubalja.

Razlika napredovanja d = 22 str.

broj koji nas zanima - vrijednost (27 + 1) člana aritmetičke progresije - očitanje brojila na kraju 27. kilometra - 27.999 ... = 28 km.

a 28 \u003d 50 + 22 ∙ (28 - 1) \u003d 644

Izračuni kalendarskih podataka za proizvoljno dugo razdoblje temelje se na formulama koje opisuju određene numeričke nizove. U astronomiji, duljina orbite geometrijski ovisi o udaljenosti nebeskog tijela do svjetiljke. Osim toga, različiti brojčani nizovi uspješno se koriste u statistici i drugim primijenjenim granama matematike.

Druga vrsta niza brojeva je geometrijska

Geometrijsku progresiju karakterizira velika, u usporedbi s aritmetičkom, stopa promjene. Nije slučajno da se u politici, sociologiji, medicini često, kako bi se prikazala velika brzina širenja određene pojave, na primjer, bolesti tijekom epidemije, kaže da se proces razvija eksponencijalno.

N-ti član niza geometrijskih brojeva razlikuje se od prethodnog po tome što se množi s nekim konstantnim brojem - nazivnik, na primjer, prvi član je 1, nazivnik je 2, odnosno:

n=1: 1 ∙ 2 = 2

n=2: 2 ∙ 2 = 4

n=3: 4 ∙ 2 = 8

n=4: 8 ∙ 2 = 16

n=5: 16 ∙ 2 = 32,

b n - vrijednost trenutnog člana geometrijske progresije;

b n+1 - formula sljedećeg člana geometrijske progresije;

q je nazivnik geometrijske progresije (konstantni broj).

Ako je graf aritmetičke progresije ravna linija, onda geometrijski crta malo drugačiju sliku:

Kao iu slučaju aritmetike, geometrijska progresija ima formulu za vrijednost proizvoljnog člana. Svaki n-ti član geometrijske progresije jednak je umnošku prvog člana i nazivnika progresije na stepen n smanjen za jedan:

Primjer. Imamo geometrijsku progresiju s prvim članom jednakim 3 i nazivnikom progresije jednakim 1,5. Pronađite 5. član progresije

b 5 \u003d b 1 ∙ q (5-1) = 3 ∙ 1,5 4 = 15,1875

Zbroj zadanog broja članova također se izračunava pomoću posebne formule. Zbroj prvih n članova geometrijske progresije jednak je razlici između umnoška n-tog člana progresije i njegovog nazivnika i prvog člana progresije, podijeljen nazivnikom smanjenim za jedan: