A veces en la vida hay situaciones en las que tienes que profundizar en tu memoria en busca de conocimientos escolares olvidados hace mucho tiempo. Por ejemplo, debe determinar el área de un terreno de forma triangular, o ha llegado el turno de la próxima reparación en un apartamento o una casa privada, y debe calcular cuánto material se necesitará para una superficie con forma triangular. Hubo un tiempo en que podías resolver ese problema en un par de minutos, y ahora estás tratando desesperadamente de recordar cómo determinar el área de un triángulo.

¡No tienes que preocuparte por esto! Después de todo, es bastante normal que el cerebro humano decida cambiar el conocimiento que no ha utilizado durante mucho tiempo a algún rincón remoto, del que a veces no es tan fácil extraerlo. Para que no tengas que sufrir con la búsqueda de conocimientos escolares olvidados para resolver tal problema, este artículo contiene varios métodos, que facilitan encontrar el área deseada del triángulo.

Es bien sabido que un triángulo es un tipo de polígono que se limita al mínimo número posible lados En principio, cualquier polígono se puede dividir en varios triángulos conectando sus vértices con segmentos que no cortan sus lados. Por lo tanto, conociendo el triángulo, puedes calcular el área de casi cualquier figura.

Entre todos los posibles triángulos que se dan en la vida, se pueden distinguir los siguientes tipos particulares: y rectangular.

La forma más sencilla de calcular el área de un triángulo es cuando uno de sus ángulos es recto, es decir, en el caso de triángulo rectángulo. Es fácil ver que es medio rectángulo. Por tanto, su área es igual a la mitad del producto de los lados, que forman un ángulo recto entre ellos.

Si conocemos la altura de un triángulo que se deja caer desde uno de sus vértices hasta lado opuesto, y la longitud de este lado, que se llama base, entonces el área se calcula como la mitad del producto de la altura por la base. Esto se escribe usando la siguiente fórmula:

S = 1/2*b*h, en el que

S es el área deseada del triángulo;

b, h - respectivamente, la altura y la base del triángulo.

Es muy fácil calcular el área. triángulo isósceles, ya que la altura dividirá en dos el lado opuesto y se puede medir fácilmente. Si se determina el área, entonces conviene tomar como altura la longitud de uno de los lados que forman ángulo recto.

Todo esto es ciertamente bueno, pero ¿cómo determinar si una de las esquinas de un triángulo es recta o no? Si el tamaño de nuestra figura es pequeño, puede usar un ángulo de construcción, un triángulo de dibujo, una postal u otro objeto con forma rectangular.

Pero, ¿y si tenemos un triángulo? parcela? En este caso, proceda de la siguiente manera: cuente desde la parte superior de la propuesta ángulo recto de un lado se mide una distancia múltiplo de 3 (30 cm, 90 cm, 3 m), y del otro lado se mide una distancia múltiplo de 4 (40 cm, 160 cm, 4 m) en la misma proporción. Ahora necesita medir la distancia entre los puntos finales de estos dos segmentos. Si el valor es un múltiplo de 5 (50 cm, 250 cm, 5 m), entonces se puede argumentar que el ángulo es recto.

Si se conoce el valor de la longitud de cada uno de los tres lados de nuestra figura, entonces el área del triángulo se puede determinar utilizando la fórmula de Heron. Para que tenga una forma más simple, se utiliza un nuevo valor, que se denomina semiperímetro. Esta es la suma de todos los lados de nuestro triángulo, dividida por la mitad. Después de calcular el semiperímetro, puede comenzar a determinar el área usando la fórmula:

S = sqrt(p(p-a)(p-b)(p-c)), donde

cuadrado- Raíz cuadrada;

p es el valor del semiperímetro (p =(a+b+c)/2);

a, b, c - bordes (lados) del triángulo.

Pero, ¿y si el triángulo tiene Forma irregular? Hay dos formas posibles aquí. El primero de ellos es tratar de dividir dicha figura en dos triángulos rectángulos, cuya suma de áreas se calcula por separado y luego se suma. O, si se conocen el ángulo entre los dos lados y el tamaño de estos lados, aplique la fórmula:

S = 0.5 * ab * sinC, donde

a,b - lados del triángulo;

c es el ángulo entre estos lados.

Este último caso es raro en la práctica, pero sin embargo, todo es posible en la vida, por lo que la fórmula anterior no será superflua. ¡Suerte con tus cálculos!

El triángulo es una figura bien conocida. Y esto, a pesar de la rica variedad de sus formas. Rectangular, equilátero, agudo, isósceles, obtuso. Cada uno de ellos es algo diferente. Pero para cualquiera se requiere saber el área del triángulo.

Fórmulas comunes para todos los triángulos que usan las longitudes de los lados o las alturas

Las designaciones adoptadas en ellos: lados - a, b, c; alturas en los lados correspondientes en a, n in, n s.

1. El área de un triángulo se calcula como el producto de ½, el lado y la altura bajada sobre él. S = ½ * a * n a. De manera similar, se deben escribir fórmulas para los otros dos lados.

2. La fórmula de Heron, en la que aparece el semiperímetro (es costumbre designarlo con una p minúscula, en contraste con el perímetro completo). El semiperímetro debe calcularse de la siguiente manera: sume todos los lados y divídalos por 2. La fórmula para el semiperímetro: p \u003d (a + b + c) / 2. Luego, la igualdad para el área de ​\u200b\u200bla figura se ve así: S \u003d √ (p * (p - a) * (p - c) * (p - c)).

3. Si no desea utilizar un semiperímetro, esta fórmula será útil, en la que solo están presentes las longitudes de los lados: S \u003d ¼ * √ ((a + b + c) * ( b + c - a) * (a + c - c) * (a + b - c)). Es algo más largo que el anterior, pero te ayudará si olvidaste cómo encontrar el semiperímetro.

Fórmulas generales en las que aparecen los ángulos de un triángulo

La notación que se requiere para leer las fórmulas: α, β, γ - ángulos. Se encuentran en lados opuestos a, b, c, respectivamente.

1. Según él, la mitad del producto de dos lados y el seno del ángulo entre ellos es igual al área del triángulo. Es decir: S = ½ a * b * sen γ. Las fórmulas para los otros dos casos deben escribirse de manera similar.

2. El área de un triángulo se puede calcular a partir de un lado y tres ángulos conocidos. S \u003d (a 2 * sin β * sin γ) / (2 sin α).

3. Hay otra fórmula con uno partido conocido y dos esquinas adyacentes. Se ve así: S = c 2 / (2 (ctg α + ctg β)).

Las dos últimas fórmulas no son las más simples. Es bastante difícil recordarlos.

Fórmulas generales para la situación cuando se conocen los radios de los círculos inscritos o circunscritos

Designaciones adicionales: r, R — radios. El primero se usa para el radio del círculo inscrito. El segundo es para el descrito.

1. La primera fórmula por la que se calcula el área de un triángulo está relacionada con el semiperímetro. S = r * r. De otra manera, se puede escribir de la siguiente manera: S \u003d ½ r * (a + b + c).

2. En el segundo caso, deberás multiplicar todos los lados del triángulo y dividirlos por el radio cuádruple del círculo circunscrito. En términos literales, se ve así: S \u003d (a * b * c) / (4R).

3. La tercera situación te permite prescindir de conocer los lados, pero necesitas los valores de los tres ángulos. S \u003d 2 R 2 * sin α * sin β * sin γ.

Caso especial: triángulo rectángulo

Esta es la situación más simple, ya que solo se requiere la longitud de ambas piernas. Se denotan con las letras latinas a y b. El área de un triángulo rectángulo es igual a la mitad del área del rectángulo que se le suma.

Matemáticamente, se ve así: S = ½ a * b. Ella es la más fácil de recordar. Como se parece a la fórmula del área de un rectángulo, solo aparece una fracción, que denota la mitad.

Caso especial: triángulo isósceles

Como sus dos lados son iguales, algunas fórmulas para su área parecen algo simplificadas. Por ejemplo, la fórmula de Heron, que calcula el área de un triángulo isósceles, toma la siguiente forma:

S = ½ pulgada √((a + ½ pulgada)*(a - ½ pulgada)).

Si lo convierte, se volverá más corto. En este caso, la fórmula de Heron para un triángulo isósceles se escribe de la siguiente manera:

S = ¼ en √(4 * a 2 - b 2).

La fórmula del área parece algo más simple que la de un triángulo arbitrario si se conocen los lados y el ángulo entre ellos. S \u003d ½ a 2 * sin β.

Caso especial: triángulo equilátero

Por lo general, en los problemas relacionados con él, el lado se conoce o se puede reconocer de alguna manera. Entonces la fórmula para encontrar el área de dicho triángulo es la siguiente:

S = (un 2 √3) / 4.

Tareas para encontrar el área si el triángulo se representa en papel cuadriculado

La situación más sencilla es cuando se dibuja un triángulo rectángulo de modo que sus catetos coincidan con las líneas del papel. Entonces solo necesita contar la cantidad de celdas que caben en las piernas. Luego multiplícalos y divídelos por dos.

Cuando el triángulo es agudo u obtuso, debe dibujarse en forma de rectángulo. Luego, en la figura resultante habrá 3 triángulos. Uno es el dado en la tarea. Y los otros dos son auxiliares y rectangulares. Las áreas de los dos últimos deben determinarse por el método descrito anteriormente. Luego calcule el área del rectángulo y réstele las calculadas para los auxiliares. Se determina el área del triángulo.

Mucho más difícil es la situación en la que ninguno de los lados del triángulo coincide con las líneas del papel. Luego se debe inscribir en un rectángulo de modo que los vértices de la figura original queden sobre sus lados. En este caso, habrá tres triángulos rectángulos auxiliares.

Un ejemplo de un problema en la fórmula de Heron

Condición. Algunos triángulos tienen lados. Son iguales a 3, 5 y 6 cm, necesitas saber su área.

Ahora puedes calcular el área de un triángulo usando la fórmula anterior. Debajo de la raíz cuadrada está el producto de cuatro números: 7, 4, 2 y 1. Es decir, el área es √ (4 * 14) = 2 √ (14).

Si no necesitas más precisión, entonces puedes sacar la raíz cuadrada de 14. Es 3,74. Entonces el área será igual a 7.48.

Responder. S \u003d 2 √14 cm 2 o 7,48 cm 2.

Un ejemplo de un problema con un triángulo rectángulo.

Condición. Un cateto de un triángulo rectángulo es 31 cm más largo que el segundo. Se requiere averiguar sus longitudes si el área del triángulo es 180 cm 2.
Solución. Tienes que resolver un sistema de dos ecuaciones. El primero tiene que ver con el área. La segunda es con la razón de los catetos, que se da en el problema.
180 \u003d ½ a * b;

a \u003d b + 31.
Primero, el valor de "a" debe sustituirse en la primera ecuación. Resulta: 180 \u003d ½ (in + 31) * in. Solo tiene una incógnita, por lo que es fácil de resolver. Después de abrir los paréntesis, obtenemos ecuación cuadrática: in 2 + 31 in - 360 = 0. Da dos valores para "in": 9 y - 40. El segundo número no es adecuado como respuesta, ya que la longitud del lado del triángulo no puede ser negativa valor.

Queda por calcular el segundo tramo: al número resultante le sumamos 31. Resulta 40. Estas son las cantidades buscadas en el problema.

Responder. Los catetos del triángulo miden 9 y 40 cm.

La tarea de hallar el lado a través del área, lado y ángulo de un triángulo

Condición. El area de algun triangulo es 60 cm2. Es necesario calcular uno de sus lados si el segundo lado mide 15 cm, y el ángulo entre ellos es de 30º.

Solución. Según las designaciones aceptadas, el lado deseado es "a", el conocido "b", el ángulo dado es "γ". Entonces la fórmula del área se puede reescribir de la siguiente manera:

60 \u003d ½ a * 15 * sen 30º. Aquí el seno de 30 grados es 0,5.

Después de las transformaciones, "a" resulta ser igual a 60 / (0,5 * 0,5 * 15). Eso es 16.

Responder. El lado deseado es de 16 cm.

El problema de un cuadrado inscrito en un triángulo rectángulo

Condición. El vértice de un cuadrado de 24 cm de lado coincide con el ángulo recto del triángulo. Los otros dos yacen sobre las piernas. El tercero pertenece a la hipotenusa. La longitud de uno de los catetos es de 42 cm ¿Cuál es el área de un triángulo rectángulo?

Solución. Considere dos triángulos rectángulos. El primero se especifica en la tarea. El segundo se basa en el cateto conocido del triángulo original. Son semejantes porque tienen un ángulo común y están formadas por rectas paralelas.

Entonces las proporciones de sus piernas son iguales. Los catetos del triángulo más pequeño miden 24 cm (lado del cuadrado) y 18 cm (dado el cateto 42 cm menos el lado del cuadrado 24 cm). Los catetos correspondientes del triángulo grande son 42 cm y x cm, es esta "x" la que se necesita para calcular el área del triángulo.

18/42 \u003d 24 / x, es decir, x \u003d 24 * 42 / 18 \u003d 56 (cm).

Entonces el área es igual al producto de 56 y 42, dividido por dos, es decir, 1176 cm 2.

Responder. El área deseada es 1176 cm 2.

Desde el vértice opuesto) y divide el producto resultante por dos. En forma se ve así:

S = ½ * a * h,

dónde:
S es el área del triángulo,
a es la longitud de su lado,
h es la altura bajada a este lado.

La longitud del lado y la altura deben presentarse en las mismas unidades. En este caso, el área del triángulo resultará en las unidades "" correspondientes.

Ejemplo.
En uno de los lados de un triángulo escaleno de 20 cm de largo, se baja una perpendicular desde el vértice opuesto de 10 cm de largo.
Se requiere el área del triángulo.
Solución.
S = ½ * 20 * 10 = 100 (cm²).

Si conoce las longitudes de dos lados cualesquiera de un triángulo escaleno y el ángulo entre ellos, utilice la fórmula:

S = ½ * a * b * senγ,

donde: a, b son las longitudes de dos lados arbitrarios y γ es el ángulo entre ellos.

En la práctica, por ejemplo, al medir terrenos, el uso de las fórmulas anteriores a veces es difícil, ya que requiere construcciones adicionales y medición de ángulos.

Si conoce las longitudes de los tres lados de un triángulo escaleno, utilice la fórmula de Heron:

S = √(p(pa)(p-b)(pc)),

a, b, c son las longitudes de los lados del triángulo,
ð – semiperímetro: p = (a+b+c)/2.

Si, además de las longitudes de todos los lados, se conoce el radio del círculo inscrito en el triángulo, utilice la siguiente fórmula compacta:

donde: r es el radio de la circunferencia inscrita (p es el semiperímetro).

Para calcular el área de un triángulo escaleno de la circunferencia circunscrita y la longitud de sus lados, utiliza la fórmula:

donde: R es el radio del círculo circunscrito.

Si se conoce la longitud de uno de los lados del triángulo y tres ángulos (en principio, dos son suficientes; el valor del tercero se calcula a partir de la igualdad de la suma de los tres ángulos del triángulo: 180º), entonces use la formula:

S = (a² * sinβ * sinγ)/2sinα,

donde α es el valor del ángulo opuesto al lado a;
β, γ son los valores de los dos ángulos restantes del triángulo.

La necesidad de encontrar varios elementos, incluyendo el área triángulo, apareció muchos siglos antes de nuestra era entre los astrónomos Antigua Grecia. Cuadrado triángulo se puede calcular diferentes caminos usando fórmulas diferentes. El método de cálculo depende de qué elementos triángulo conocido.

Instrucción

Si de la condición conocemos los valores de los dos lados b, c y el ángulo formado por ellos?, entonces el área triángulo ABC se encuentra mediante la fórmula:
S = (bcsen?)/2.

Si de la condición conocemos los valores de los dos lados a, b y el ángulo que no forman ellos?, entonces el área triángulo ABC se encuentra de la siguiente manera:
¿Encontrar el ángulo?, ¿pecado? = bsin? / a, más adelante en la tabla determinamos el ángulo en sí.
¿Encontrar un ángulo? = 180°-?-?.
Encuentre el área misma S = (¿absin?)/2.

Si de la condición conocemos los valores de solo tres lados triángulo a, b y c, entonces el área triángulo ABC se encuentra mediante la fórmula:
S = v(p(p-a)(p-b)(p-c)) , donde p es el semiperímetro p = (a+b+c)/2

Si a partir de la condición del problema conocemos la altura triángulo h y el lado al que se baja esta altura, entonces el área triángulo ABC por fórmula:
S = ah(a)/2 = bh(b)/2 = ch(c)/2.

Si conocemos los valores de los lados triángulo a, b, c y el radio de la circunscrita cerca de la dada triángulo R, entonces el área de este triángulo ABC está determinado por la fórmula:
S = abc/4R.
Si se conocen los tres lados a, b, c y el radio de los inscritos, entonces el área triángulo ABC se encuentra mediante la fórmula:
S = pr, donde p es el semiperímetro, p = (a+b+c)/2.

Si ABC es equilátero, entonces el área se encuentra mediante la fórmula:
S = (a^2v3)/4.
Si el triángulo ABC es isósceles, entonces el área está determinada por la fórmula:
S = (cv(4a^2-c^2))/4, donde c es triángulo.
Si el triángulo ABC es un triángulo rectángulo, entonces el área está determinada por la fórmula:
S = ab/2, donde a y b son catetos triángulo.
Si el triángulo ABC es un triángulo isósceles rectángulo, entonces el área está determinada por la fórmula:
S = c^2/4 = a^2/2, donde c es la hipotenusa triángulo, a=b - pierna.

Videos relacionados

Fuentes:

• como medir el area de un triangulo

Consejo 3: Cómo encontrar el área de un triángulo si conoces el ángulo

Saber solo un parámetro (el valor del ángulo) no es suficiente para encontrar el área tres cuadrado . Si hay dimensiones adicionales, para determinar el área, puede elegir una de las fórmulas en las que el valor del ángulo también se usa como una de las variables conocidas. Algunas de las fórmulas más utilizadas se enumeran a continuación.

Instrucción

Si además del ángulo (γ) formado por los dos lados tres cuadrado , también se conocen las longitudes de estos lados (A y B), entonces cuadrado Las figuras (S) se pueden definir como la mitad del producto de las longitudes de los lados y el seno de este ángulo conocido: S=½×A×B×sin(γ).

El concepto de área

El concepto de área de cualquier figura geometrica, en particular un triángulo, asociaremos con tal figura como un cuadrado. Para una unidad de área de cualquier figura geométrica, tomaremos el área de un cuadrado, cuyo lado es igual a uno. Para completar, recordamos dos propiedades básicas para el concepto de áreas de formas geométricas.

Propiedad 1: Si las formas geométricas son iguales, entonces sus áreas también son iguales.

Propiedad 2: Cualquier figura se puede dividir en varias figuras. Además, el área de la figura original es igual a la suma de los valores de las áreas de todas las figuras que la componen.

Considere un ejemplo.

Ejemplo 1

Es obvio que uno de los lados del triángulo es la diagonal del rectángulo, donde un lado es $5$ (ya que las celdas son $5$) y el otro es $6$ (ya que las celdas son $6$). Por tanto, el área de este triángulo será igual a la mitad de dicho rectángulo. el area del rectangulo es

entonces el area del triangulo es

Respuesta: $15$.

Luego, considere varios métodos para encontrar las áreas de los triángulos, es decir, usando la altura y la base, usando la fórmula de Heron y el área de un triángulo equilátero.

Como sacar el area de un triangulo usando la altura y la base

Teorema 1

El área de un triángulo se puede encontrar como la mitad del producto de la longitud de un lado por la altura dibujada hacia ese lado.

Matemáticamente se ve así

$S=\frac(1)(2)αh$

donde $a$ es la longitud del lado, $h$ es la altura dibujada hacia él.

Prueba.

Considere el triángulo $ABC$ donde $AC=α$. La altura $BH$ se dibuja hacia este lado y es igual a $h$. Construyámoslo hasta el cuadrado $AXYC$ como en la Figura 2.

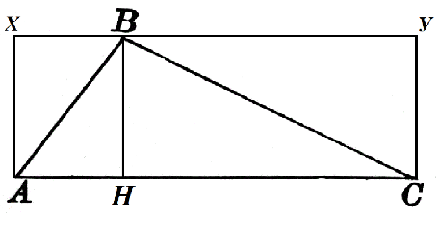
El área del rectángulo $AXBH$ es $h\cdot AH$, y la del rectángulo $HBYC$ es $h\cdot HC$. Después

$S_ABH=\frac(1)(2)h\cdot AH$, $S_CBH=\frac(1)(2)h\cdot HC$

Por tanto, el área buscada del triángulo, según la propiedad 2, es igual a

$S=S_ABH+S_CBH=\frac(1)(2)h\cdot AH+\frac(1)(2)h\cdot HC=\frac(1)(2)h\cdot (AH+HC)=\ fracción(1)(2)αh$

El teorema ha sido probado.

Ejemplo 2

Encuentre el área del triángulo en la figura a continuación, si la celda tiene un área igual a uno

La base de este triángulo es $9$ (ya que $9$ son celdas de $9$). La altura también es $9$. Entonces, por el Teorema 1, obtenemos

$S=\frac(1)(2)\cdot 9\cdot 9=40.5$

Respuesta: $40.5$.

fórmula de garza

Teorema 2

Si nos dan los tres lados de un triángulo $α$, $β$ y $γ$, entonces su área se puede encontrar de la siguiente manera

$S=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

aquí $ρ$ significa la mitad del perímetro de este triángulo.

Prueba.

Considere la siguiente figura:

Por el teorema de Pitágoras, del triángulo $ABH$ obtenemos

Del triángulo $CBH$, por el teorema de Pitágoras, tenemos

$h^2=α^2-(β-x)^2$

$h^2=α^2-β^2+2βx-x^2$

De estas dos relaciones obtenemos la igualdad

$γ^2-x^2=α^2-β^2+2βx-x^2$

$x=\frac(γ^2-α^2+β^2)(2β)$

$h^2=γ^2-(\frac(γ^2-α^2+β^2)(2β))^2$

$h^2=\frac((α^2-(γ-β)^2)((γ+β)^2-α^2))(4β^2)$

$h^2=\frac((α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α))(4β^2)$

Como $ρ=\frac(α+β+γ)(2)$, entonces $α+β+γ=2ρ$, por lo tanto

$h^2=\frac(2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α))(4β^2)$

$h^2=\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2 )$

$h=\sqrt(\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2))$

$h=\frac(2)(β)\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

Por el Teorema 1, obtenemos

$S=\frac(1)(2) βh=\frac(β)(2)\cdot \frac(2)(β) \sqrt(ρ(ρ-α)(ρ-β)(ρ-γ) )=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

Un triángulo es la figura geométrica más simple, que consta de tres lados y tres vértices. Por su sencillez, el triángulo se ha utilizado desde la antigüedad para sujetar varias medidas, y hoy la figura puede ser útil para resolver problemas prácticos y cotidianos.

Características del triángulo

La figura se ha utilizado para cálculos desde la antigüedad, por ejemplo, topógrafos y astrónomos operan con las propiedades de los triángulos para calcular áreas y distancias. A través del área de esta figura, es fácil expresar el área de cualquier n-ágono, y los científicos antiguos utilizaron esta propiedad para derivar fórmulas para las áreas de los polígonos. El trabajo constante con triángulos, especialmente con un triángulo rectángulo, se ha convertido en la base de toda una sección de matemáticas: la trigonometría.

geometría triangular

Las propiedades de la figura geométrica se han estudiado desde la antigüedad: la información más antigua sobre el triángulo se encontró en papiros egipcios de 4000 años. Luego se estudió la figura en la antigua Grecia y la mayor contribución a la geometría del triángulo la hicieron Euclides, Pitágoras y Garza. El estudio del triángulo nunca se detuvo, y en el siglo XVIII Leonhard Euler introdujo el concepto de ortocentro de la figura y el círculo de Euler. A finales del siglo XIX y XX, cuando parecía que se sabía absolutamente todo sobre el triángulo, Frank Morley formuló el teorema de la trisectriz del ángulo y Vaclav Sierpinski propuso el triángulo fractal.

Hay varios tipos de triángulos planos que nos son familiares del curso de geometría escolar:

• ángulo agudo: todas las esquinas de la figura son afiladas;
• obtuso - la figura tiene uno ángulo obtuso(más de 90 grados);
• rectangular: la figura contiene un ángulo recto igual a 90 grados;
• isósceles - un triángulo con dos lados iguales;
• equilátero - un triángulo con todos los lados iguales.
• A vida real hay todo tipo de triángulos, y en algunos casos puede que necesitemos calcular el área de una figura geométrica.

Area de un triangulo

El área es una estimación de cuánto del plano limita la figura. El área de un triángulo se puede encontrar de seis formas, usando los lados, la altura, los ángulos, el radio de un círculo inscrito o circunscrito, así como usando la fórmula de Heron o calculando una integral doble sobre las líneas que delimitan el plano. La fórmula más sencilla para calcular el área de un triángulo es:

donde a es el lado del triángulo, h es su altura.

Sin embargo, en la práctica no siempre nos conviene encontrar la altura de una figura geométrica. El algoritmo de nuestra calculadora le permite calcular el área sabiendo:

• tres lados;
• dos lados y el ángulo entre ellos;
• un lado y dos esquinas.

Para determinar el área en términos de tres lados, usamos la fórmula de Heron:

S = raíz cuadrada (p × (p-a) × (p-b) × (p-c)),

donde p es el medio perímetro del triángulo.

El cálculo del área de dos lados y un ángulo se realiza según la fórmula clásica:

S = a × b × sin(alfa),

donde alfa es el ángulo entre los lados a y b.

Para determinar el área a través de un lado y dos esquinas usamos la relación que:

a / sin(alfa) = b / sin(beta) = c / sin(gamma)

Usando una proporción simple, determinamos la longitud del segundo lado, después de lo cual calculamos el área usando la fórmula S = a × b × sin(alfa). este algoritmo completamente automatizado y solo necesita ingresar las variables especificadas y obtener el resultado. Veamos un par de ejemplos.

ejemplos de la vida real

Lajas para piso

Supongamos que desea pavimentar el piso con baldosas triangulares y determinar la cantidad material requerido, debe averiguar el área de una baldosa y el área del piso. Supongamos que necesita procesar 6 metros cuadrados de una superficie usando mosaicos cuyas dimensiones son a \u003d 20 cm, b \u003d 21 cm, c \u003d 29 cm. Obviamente, para calcular el área de un triángulo, el calculadora utiliza la fórmula de Heron y dará el resultado:

Por lo tanto, el área de un elemento de mosaico será de 0,021 metros cuadrados, y necesitará 6 / 0,021 \u003d 285 triángulos para mejorar el piso. Los números 20, 21 y 29 forman los números triples pitagóricos que satisfacen . Y así es, nuestra calculadora también calculó todos los ángulos del triángulo, y el ángulo gamma es exactamente de 90 grados.

tarea escolar

En un problema escolar, debe encontrar el área de un triángulo, sabiendo que el lado a \u003d 5 cm y los ángulos alfa y beta de la herida son 30 y 50 grados, respectivamente. Para resolver este problema manualmente, primero encontraríamos el valor del lado b usando la razón de los lados y los senos de los ángulos opuestos, y luego determinaríamos el área usando la fórmula simple S = a × b × sin(alfa). Ahorremos tiempo, ingrese los datos en el formulario de la calculadora y obtenga una respuesta instantánea

Al usar una calculadora, es importante especificar correctamente los ángulos y los lados, de lo contrario, el resultado será incorrecto.

Conclusión

El triángulo es una figura única que ocurre tanto en la vida real como en cálculos abstractos. Usa nuestra calculadora en línea para encontrar el área de triángulos de cualquier tipo.