Príklady delenia desatinných miest celým číslom. Zostavenie sústavy rovníc

Pridávanie desatinných miest sa vykonáva rovnakým spôsobom ako pridávanie celých čísel. Pozrime sa na to na príkladoch.

1) 0,132 + 2,354. Podpíšme pojmy jeden pod druhým.

Tu sa zo súčtu 2 tisícin so 4 tisícinami získalo 6 tisícin;
z pripočítania 3 stotín s 5 stotinami vyšlo 8 stotín;
od pridania 1 desatiny s 3 desatinami -4 desatiny a
zo sčítania 0 celých čísel s 2 celými číslami - 2 celé čísla.

2) 5,065 + 7,83.

V druhom termíne nie sú žiadne tisíciny, preto je dôležité nepomýliť sa pri podpisovaní podmienok pod seba.

3) 1,2357 + 0,469 + 2,08 + 3,90701.

Tu, keď pripočítame tisíciny, dostaneme 21 tisícin; napísali sme 1 pod tisíciny a 2 pridali na stotiny, takže na stom mieste sme dostali tieto výrazy: 2 + 3 + 6 + 8 + 0; v súčte dávajú 19 stotín, my sme podpísali 9 pod stotiny a 1 sa počítala ako desatiny atď.

Pri pridávaní desatinných zlomkov je teda potrebné dodržiavať ďalšia objednávka: zlomky podpíšte tak, aby vo všetkých členoch boli pod sebou rovnaké číslice a všetky čiarky boli v rovnakom zvislom stĺpci; napravo od desatinných miest niektorých výrazov pripisujú aspoň mentálne taký počet núl, aby všetky výrazy za desatinnou čiarkou mali rovnaké čísločíslic. Potom sa vykoná sčítanie číslicami, počnúc od pravej strany a vo výslednom množstve sa čiarka umiestni do rovnakého zvislého stĺpca, ako je to v týchto výrazoch.

§ 108. Odčítanie desatinných zlomkov.

Odčítanie desatinných miest sa vykonáva rovnakým spôsobom ako odčítanie celých čísel. Ukážme si to na príkladoch.

1) 9,87 - 7,32. Podpisujme subtrahend pod minuend tak, aby jednotky tej istej číslice boli pod sebou:

2) 16,29 - 4,75. Podpíšme subtrahend pod minuend, ako v prvom príklade:

Na odčítanie desiatok bolo potrebné vziať jednu celú jednotku zo 6 a rozdeliť ju na desatiny.

3) 14,0213-5,350712. Podpíšme subtrahend pod minuend:

Odčítanie sa uskutočnilo nasledovne: keďže od 0 nemôžeme odpočítať 2 milióntiny, mali by sme sa odvolávať na najbližšiu číslicu vľavo, t. j. na stotisíciny, ale namiesto stotisíciny je aj nula, takže vezmeme 1 desaťtisícina z 3 desaťtisícin a rozdelíme to na stotisíciny, dostaneme 10 stotisíc, z ktorých 9 stotisíc zostane v kategórii stotisíc a 1 stotisícina sa rozdrví na miliontiny, dostaneme 10 miliónov. Teda v posledné tričíslice, ktoré sme dostali: milióntiny 10, stotisíciny 9, desaťtisíciny 2. Pre väčšiu prehľadnosť a pohodlie (nezabudnúť) sú tieto čísla napísané na vrchu zodpovedajúcich zlomkových číslic redukovaného. Teraz môžeme začať odčítavať. Odčítame 2 milióntiny od 10 milióntin, dostaneme 8 milióntin; odpočítajte 1 stotisícinu od 9 stotisíc, dostaneme 8 stotisíc atď.

Pri odčítaní desatinných zlomkov sa teda dodržiava nasledovné poradie: podradník sa podpíše pod redukovaný tak, že rovnaké číslice sú jedna pod druhou a všetky čiarky sú v rovnakom zvislom stĺpci; vpravo pripisujú, aspoň mentálne, v zmenšenom alebo odčítanom toľko núl, aby mali rovnaký počet číslic, potom odčítajú po čísliciach, začínajúc od pravej strany a vo výslednom rozdiele dajú čiarku do rovnaký vertikálny stĺpec, v ktorom sa nachádza v redukovanom a odčítanom.

§ 109. Násobenie desatinných zlomkov.

Zvážte niekoľko príkladov násobenia desatinných zlomkov.

Aby sme našli súčin týchto čísel, môžeme uvažovať takto: ak sa faktor zvýši 10-krát, potom oba faktory budú celé čísla a potom ich môžeme vynásobiť podľa pravidiel pre násobenie celých čísel. Ale vieme, že keď sa jeden z faktorov zvýši niekoľkokrát, produkt sa zvýši o rovnakú hodnotu. To znamená, že číslo, ktoré je výsledkom vynásobenia celočíselných faktorov, t. j. 28 x 23, je 10-krát väčšie ako skutočný súčin, a aby ste získali skutočný súčin, musíte 10-krát znížiť nájdený súčin. Preto tu musíte raz vykonať násobenie 10 a raz delenie 10, ale násobenie a delenie 10 sa vykonáva posunutím čiarky doprava a doľava o jedno znamienko. Preto musíte urobiť toto: v multiplikátore posuňte čiarku doprava o jedno znamienko, z toho sa bude rovnať 23, potom musíte vynásobiť výsledné celé čísla:

Tento produkt je 10-krát väčší ako skutočný. Preto ho treba zmenšiť 10-krát, za čo posunieme čiarku o jeden znak doľava. Tak dostaneme

28 2,3 = 64,4.

Pre účely overenia môžete napísať desatinný zlomok s menovateľom a vykonať akciu podľa pravidla pre násobenie obyčajných zlomkov, t.j.

2) 12,27 0,021.

Rozdiel medzi týmto príkladom a predchádzajúcim je v tom, že tu sú oba faktory reprezentované desatinnými zlomkami. Tu však v procese násobenia nebudeme venovať pozornosť čiarkam, to znamená, že násobiteľ dočasne zvýšime 100-krát a násobiteľ 1 000-krát, čím sa súčin zväčší 100 000-krát. Vynásobením 1227 číslom 21 teda dostaneme:

1 227 21 = 25 767.

Ak vezmeme do úvahy, že výsledný produkt je 100 000-krát väčší ako skutočný, musíme ho teraz zmenšiť 100 000-krát správnym umiestnením čiarky, potom dostaneme:

32,27 0,021 = 0,25767.

Skontrolujme to:

Na vynásobenie dvoch desatinných zlomkov teda stačí, bez toho, aby sme dávali pozor na čiarky, vynásobiť ich ako celé čísla a v súčine oddeliť čiarkou na pravej strane toľko desatinných miest, koľko bolo v násobilke a v faktor spolu.

V poslednom príklade je výsledkom súčin s piatimi desatinnými miestami. Ak sa takáto väčšia presnosť nevyžaduje, vykoná sa zaokrúhľovanie. desatinný zlomok. Pri zaokrúhľovaní by ste mali použiť rovnaké pravidlo, aké bolo uvedené pre celé čísla.

§ 110. Násobenie pomocou tabuliek.

Násobenie desatinných miest možno niekedy vykonať pomocou tabuliek. Na tento účel môžete použiť napríklad násobilky dvojciferné čísla, ktorého popis bol uvedený skôr.

1) Vynásobte číslo 53 číslom 1,5.

53 vynásobíme 15. V tabuľke sa tento súčin rovná 795. Našli sme súčin 53 krát 15, ale náš druhý faktor bol 10x menší, to znamená, že súčin treba zmenšiť 10x, t.j.

53 1,5 = 79,5.

2) Vynásobte 5,3 číslom 4,7.

Najprv v tabuľke nájdeme súčin 53 krát 47, bude to 2491. Ale keďže sme násobiteľ a násobiteľ zvýšili celkovo 100-krát, tak výsledný súčin je 100-krát väčší, ako by mal byť; takže musíme znížiť tento produkt o faktor 100:

5,3 4,7 = 24,91.

3) Vynásobte 0,53 číslom 7,4.

Najprv nájdeme v tabuľke súčin 53 x 74; to bude 3 922. Ale keďže sme zvýšili násobiteľ 100-krát a násobiteľ 10-krát, súčin sa zvýšil 1 000-krát; takže ho teraz musíme znížiť 1000:

0,53 7,4 = 3,922.

§ 111. Delenie desatinných miest.

Na desatinné delenie sa pozrieme v tomto poradí:

1. Desatinné delenie podľa celé číslo,

1. Delenie desatinného zlomku celým číslom.

1) Vydeľte 2,46 číslom 2.

Najprv sme vydelili 2 celé čísla, potom desatiny a nakoniec stotiny.

2) Vydeľte 32,46 číslom 3.

32,46: 3 = 10,82.

Vydelili sme 3 desiatky 3, potom sme začali deliť 2 jednotky 3; od počtu jednotiek dividendy (2) menší deliteľ(3), potom som musel dať 0 do kvocientu; ďalej na zvyšok sme zbúrali 4 desatiny a 24 desatín rozdelili 3; dostal v súkromí 8 desatín a napokon rozdelil 6 stotín.

3) Vydeľte 1,2345 číslom 5.

1,2345: 5 = 0,2469.

Tu, v kvociente na prvom mieste, sa ukázalo nula celých čísel, pretože jedno celé číslo nie je deliteľné 5.

4) Vydeľte 13,58 číslom 4.

Zvláštnosťou tohto príkladu je, že keď sme súkromne dostali 9 stotín, potom sa našiel zvyšok rovnajúci sa 2 stotinám, tento zvyšok sme rozdelili na tisíciny, dostali 20 tisícin a doviedli delenie do konca.

Pravidlo. Delenie desatinného zlomku celým číslom sa vykonáva rovnakým spôsobom ako delenie celých čísel a výsledné zvyšky sa premieňajú na desatinné zlomky, stále menšie; delenie pokračuje, kým sa zvyšok nerovná nule.

2. Delenie desatinného zlomku desatinným zlomkom.

1) Vydeľte 2,46 číslom 0,2.

Už vieme, ako deliť desatinný zlomok celým číslom. Zamyslime sa nad tým, či sa dá tento nový prípad rozdelenia zredukovať aj na ten predchádzajúci? Kedysi sme považovali za pozoruhodnú vlastnosť kvocientu, ktorá spočíva v tom, že zostáva nezmenený pri rovnakom násobnom zvýšení alebo znížení dividendy a deliteľa. Kľudne by sme vykonali delenie ponúkaných čísel, ak by deliteľom bolo celé číslo. Na to ho stačí zvýšiť 10-krát a na získanie správneho kvocientu je potrebné zvýšiť dividendu o rovnaký počet, teda 10-krát. Potom bude delenie týchto čísel nahradené delením takýchto čísel:

a nie je potrebné robiť žiadne zmeny v súkromí.

Urobme toto rozdelenie:

Takže 2,46: 0,2 = 12,3.

2) Vydeľte 1,25 číslom 1,6.

Deliteľa (1,6) zväčšíme 10-krát; aby sa podiel nezmenil, zvýšime dividendu 10-krát; 12 celých čísel nie je deliteľných 16, preto píšeme v kvociente 0 a 125 desatín delíme 16, dostaneme 7 desatín v kvociente a zvyšok je 13. 13 desatín rozdelíme na stotiny priradením nuly a 130 stotín delíme 16 atď. Venujte pozornosť nasledujúcemu:

a) keď sa v kvociente nezískajú celé čísla, na ich miesto sa zapíšu nulové celé čísla;

b) keď sa po prepočítaní číslice dividendy na zvyšok získa číslo, ktoré nie je deliteľné deliteľom, potom sa do podielu zapíše nula;

c) keď sa po odstránení poslednej číslice dividendy delenie nekončí, potom priradením nuly k zvyškom delenie pokračuje;

d) ak je dividenda celé číslo, potom pri jej delení desatinným zlomkom sa jej zvýšenie vykoná priradením núl.

Ak teda chcete deliť číslo desatinným zlomkom, musíte v deliteľovi zahodiť čiarku a potom zvýšiť deliteľ toľkokrát, koľkokrát sa deliteľ zvýšil, keď v ňom padla čiarka, a potom vykonať delenie podľa pravidlo delenia desatinného zlomku celým číslom.

§ 112. Približný podiel.

V predchádzajúcom odseku sme uvažovali o delení desatinných zlomkov a vo všetkých príkladoch, ktoré sme riešili, bolo delenie ukončené, t. j. získal sa presný kvocient. Vo väčšine prípadov však nie je možné získať presný kvocient, bez ohľadu na to, ako ďaleko predĺžime delenie. Tu je jeden taký prípad: vydeľte 53 číslom 101.

Už sme dostali päť číslic v kvociente, ale delenie sa ešte neskončilo a nie je nádej, že sa niekedy skončí, pretože čísla, s ktorými sme sa predtým stretli, sa začínajú objavovať vo zvyšku. Čísla sa budú tiež opakovať v kvociente: samozrejme, po čísle 7 sa objaví číslo 5, potom 2 atď. bez konca. V takýchto prípadoch je delenie prerušené a obmedzené na niekoľko prvých číslic kvocientu. Tento súkromný je tzv približné. Ako vykonať rozdelenie v tomto prípade, ukážeme na príkladoch.

Nech je potrebné deliť 25 3. Je zrejmé, že z takéhoto delenia nie je možné získať presný kvocient vyjadrený ako celé číslo alebo desatinný zlomok. Preto budeme hľadať približný kvocient:

25: 3 = 8 a zvyšok 1

Približný podiel je 8; je to samozrejme menej ako presný kvocient, pretože je tam zvyšok 1. Ak chcete získať presný kvocient, musíte k nájdenému približnému kvocientu, teda k 8, pridať zlomok, ktorý vznikne delením zvyšku. , rovná 1, 3; bude to zlomok 1/3. To znamená, že presný kvocient bude vyjadrený ako zmiešané číslo 8 1/3. Keďže 1/3 je správny zlomok, t.j. zlomok, menej ako jeden, potom predpokladáme, že ho zahodíme chyba, ktorý menej ako jeden . Súkromný 8 bude približný kvocient do jednej s nevýhodou. Ak vezmeme 9 namiesto 8, povolíme aj chybu, ktorá je menšia ako jedna, pretože nepridáme celú jednotku, ale 2/3. Taký súkromný závet približný kvocient do jednej s prebytkom.

Uveďme si teraz ďalší príklad. Nech je potrebné deliť 27 8. Keďže tu nedostaneme presný kvocient vyjadrený ako celé číslo, budeme hľadať približný kvocient:

27: 8 = 3 a zvyšok 3.

Chyba je tu 3/8, je menšia ako jedna, čo znamená, že približný kvocient (3) sa nachádza až do jednej s nevýhodou. Pokračujeme v delení: zvyšok 3 rozdelíme na desatiny, dostaneme 30 desatín; Vydelme ich 8.

Dostali sme v súkromí na mieste desatiny 3 a vo zvyšku b desatiny. Ak sa obmedzíme najmä na číslo 3,3 a zvyšok 6 zahodíme, pripustíme chybu menšiu ako jednu desatinu. prečo? Pretože presný kvocient by sme získali, keby sme k 3,3 pridali výsledok delenia 6 desatín 8; z tohto delenia by bolo 6/80, čo je menej ako jedna desatina. (Skontrolujte!) Ak sa teda obmedzíme na desatiny v kvociente, potom môžeme povedať, že sme našli kvocient s presnosťou na jednu desatinu(s nevýhodou).

Pokračujme v delení, aby sme našli ešte jedno desatinné miesto. Aby sme to urobili, rozdelíme 6 desatín na stotiny a dostaneme 60 stotín; Vydelme ich 8.

V súkromí na treťom mieste to dopadlo 7 a vo zvyšku 4 stotiny; ak ich zahodíme, tak pripustíme chybu menšiu ako stotinu, pretože 4 stotiny delené 8 sú menej ako jedna stotina. V takýchto prípadoch sa hovorí, že kvocient sa nájde. s presnosťou na stotinu(s nevýhodou).

V príklade, ktorý teraz zvažujeme, môžete získať presný kvocient vyjadrený ako desatinný zlomok. Na to stačí rozdeliť posledný zvyšok, 4 stotiny, na tisíciny a rozdeliť 8.

V drvivej väčšine prípadov je však nemožné získať presný kvocient a treba sa obmedziť na jeho približné hodnoty. Teraz zvážime takýto príklad:

40: 7 = 5,71428571...

Bodky na konci čísla označujú, že delenie nie je dokončené, to znamená, že rovnosť je približná. Približná rovnosť sa zvyčajne píše takto:

40: 7 = 5,71428571.

Vzali sme kvocient s ôsmimi desatinnými miestami. Ale ak nie je potrebná taká veľká presnosť, možno sa obmedziť na celú časť kvocientu, t.j. číslo 5 (presnejšie 6); pre väčšiu presnosť by sa mohli brať do úvahy desatiny a kvocient by sa mal rovnať 5,7; ak je táto presnosť z nejakého dôvodu nedostatočná, tak sa môžeme zastaviť na stotinách a zobrať 5,71 atď.. Vypíšme si jednotlivé kvocienty a pomenujme ich.

Prvý približný kvocient do jednej 6.

Druhá » » » až jedna desatina 5.7.

Tretia » » » do stotiny 5,71.

Štvrtá » » » až jedna tisícina z 5,714.

Aby sa teda našiel približný kvocient s presnosťou napríklad na 3. desatinné miesto (t.j. do jednej tisíciny), delenie sa zastaví hneď po nájdení tohto znamienka. V tomto prípade treba pamätať na pravidlo uvedené v § 40.

§ 113. Najjednoduchšie problémy pre úrok.

Po preštudovaní desatinných zlomkov vyriešime ešte niekoľko percentuálnych úloh.

Tieto úlohy sú podobné tým, ktoré sme riešili v oddelení obyčajných zlomkov; ale teraz budeme písať stotiny vo forme desatinných zlomkov, teda bez výslovne určeného menovateľa.

V prvom rade musíte vedieť jednoducho prejsť z obyčajného zlomku na desatinný zlomok s menovateľom 100. Aby ste to dosiahli, musíte čitateľa vydeliť menovateľom:

Nasledujúca tabuľka ukazuje, ako sa číslo so symbolom % (v percentách) nahradí desatinnou čiarkou s menovateľom 100:

Uvažujme teraz o niekoľkých problémoch.

1. Nájdenie percent daného čísla.

Úloha 1. V jednej obci žije len 1600 ľudí. Počet detí v školskom veku je 25 %. celkový počet obyvateľov. Koľko školopovinných detí je v tejto obci?

V tomto probléme musíte nájsť 25 % alebo 0,25 z 1 600. Problém je vyriešený vynásobením:

1 600 0,25 = 400 (deti).

Preto 25 % z 1 600 je 400.

Pre jasné pochopenie tejto úlohy je užitočné pripomenúť, že na sto obyvateľov pripadá 25 školopovinných detí. Preto, aby ste zistili počet všetkých školopovinných detí, môžete najprv zistiť, koľko stoviek je v čísle 1600 (16), a potom vynásobiť 25 počtom stoviek (25 x 16 = 400). Týmto spôsobom môžete skontrolovať platnosť riešenia.

Úloha 2. Sporiteľne dávajú vkladateľom 2 % z príjmu ročne. Koľko príjmu za rok dostane vkladateľ, ktorý vložil: a) 200 rubľov? b) 500 rubľov? c) 750 rubľov? d) 1000 rubľov?

Vo všetkých štyroch prípadoch bude na vyriešenie problému potrebné vypočítať 0,02 z uvedených súm, t.j. každé z týchto čísel bude potrebné vynásobiť 0,02. Poďme na to:

a) 200 0,02 = 4 (ruble),

b) 500 0,02 = 10 (rubľov),

c) 750 0,02 = 15 (rubľov),

d) 1 000 0,02 = 20 (rubľov).

Každý z týchto prípadov možno overiť nasledujúcimi úvahami. Sporiteľne dávajú vkladateľom 2 % z príjmu, teda 0,02 zo sumy vloženej do sporenia. Ak by suma bola 100 rubľov, potom 0,02 z toho by boli 2 ruble. To znamená, že každých sto prináša vkladateľovi 2 ruble. príjem. Preto v každom z uvažovaných prípadov stačí zistiť, koľko stoviek je v danom čísle, a vynásobiť 2 ruble týmto počtom stoviek. V príklade a) stovky 2, tak

2 2 \u003d 4 (ruble).

V príklade d) sú stovky 10, čo znamená

2 10 \u003d 20 (rubľov).

2. Nájdenie čísla podľa jeho percent.

Úloha 1. Na jar školu maturovalo 54 žiakov, čo je 6 % z celkového počtu žiakov. Koľko žiakov bolo v škole v minulosti akademický rok?

Najprv si objasnime význam tohto problému. Školu ukončilo 54 žiakov, čo je 6 % z celkového počtu žiakov, resp. 6 stotín (0,06) všetkých žiakov školy. To znamená, že poznáme časť žiakov vyjadrenú číslom (54) a zlomkom (0,06) a z tohto zlomku musíme nájsť celé číslo. Pred nami je teda obyčajný problém nájsť číslo podľa jeho zlomku (§ 90 ods. 6). Problémy tohto typu sa riešia delením:

To znamená, že v škole bolo 900 žiakov.

Takéto úlohy je užitočné skontrolovať vyriešením inverznej úlohy, t. j. po vyriešení úlohy by ste mali, aspoň vo svojej mysli, vyriešiť úlohu prvého typu (zistenie percenta daného čísla): vezmite nájdené číslo ( 900) ako je uvedené a nájdite z neho percento uvedené v riešenom probléme, a to:

900 0,06 = 54.

Úloha 2. Na jedlo rodina počas mesiaca minie 780 rubľov, čo je 65 % mesačného príjmu otca. Určite jeho mesačný príjem.

Táto úloha má rovnaký význam ako predchádzajúca. Uvádza časť mesačného zárobku vyjadrenú v rubľoch (780 rubľov) a uvádza, že táto časť predstavuje 65 % alebo 0,65 celkových zárobkov. A požadovaný je celý zárobok:

780: 0,65 = 1 200.

Preto je požadovaný zárobok 1200 rubľov.

3. Zistenie percenta čísel.

Úloha 1.Školská knižnica má spolu 6000 kníh. Medzi nimi je 1200 kníh o matematike. Koľko percent matematických kníh tvorí celkový počet kníh v knižnici?

Tento druh problému sme už zvažovali (§97) a dospeli sme k záveru, že na výpočet percenta dvoch čísel musíte nájsť pomer týchto čísel a vynásobiť ho 100.

V našej úlohe musíme nájsť percentuálny podiel čísel 1 200 a 6 000.

Najprv zistíme ich pomer a potom ho vynásobíme 100:

Percento čísel 1 200 a 6 000 je teda 20. Inými slovami, matematické knihy tvoria 20 % z celkového počtu všetkých kníh.

Na kontrolu riešime inverzný problém: nájdite 20 % zo 6 000:

6 000 0,2 = 1 200.

Úloha 2. Závod by mal dostať 200 ton uhlia. Dodaných už bolo 80 ton Koľko percent uhlia bolo dodaných do závodu?

Tento problém sa pýta, koľko percent je jedno číslo (80) od druhého (200). Pomer týchto čísel bude 80/200. Vynásobme to 100:

To znamená, že bolo dodaných 40 % uhlia.

V tomto článku budeme analyzovať takú dôležitú akciu s desatinnými zlomkami, ako je delenie. Najprv formulujeme všeobecné zásady, potom si rozoberieme, ako správne rozdeliť desatinné zlomky podľa stĺpca na iné zlomky aj na prirodzené čísla. Ďalej si rozoberieme delenie obyčajných zlomkov na desatinné a naopak a na záver si ukážeme, ako správne deliť zlomky končiace na 0, 1, 0, 01, 100, 10 atď.

Tu berieme len prípady s kladnými zlomkami. Ak je pred zlomkom mínus, musíte s ním konať, musíte si preštudovať materiál o rozdelení racionálnych a reálnych čísel.

Yandex.RTB R-A-339285-1

Všetky desatinné zlomky, konečné aj periodické, sú len špeciálnou formou zápisu obyčajných zlomkov. Preto pre ne platia rovnaké princípy ako pre im zodpovedajúce obyčajné zlomky. Celý proces delenia desatinných zlomkov teda redukujeme na ich nahradenie obyčajnými, po čom nasleduje výpočet nám už známymi metódami. Uveďme si konkrétny príklad.

Príklad 1

Vydeľte 1,2 číslom 0,48.

rozhodnutie

Desatinné zlomky píšeme v tvare obyčajných zlomkov. Budeme môcť:

1 , 2 = 12 10 = 6 5

0 , 48 = 48 100 = 12 25 .

Potrebujeme teda vydeliť 6 5 číslom 12 25 . My veríme:

1, 2: 0, 48 = 6 2: 12 25 = 6 5 25 12 = 6 25 5 12 = 5 2

Z výsledného nesprávny zlomok môžete vybrať celú časť a získať zmiešané číslo 2 1 2, alebo ho môžete reprezentovať ako desatinný zlomok tak, aby sa zhodoval s pôvodnými číslami: 5 2 \u003d 2, 5. Ako to urobiť, sme už napísali skôr.

odpoveď: 1 , 2: 0 , 48 = 2 , 5 .

Príklad 2

Vypočítajte, koľko bude 0 , (504) 0 , 56 .

rozhodnutie

Najprv musíme previesť periodický desatinný zlomok na obyčajný.

0 , (504) = 0 , 504 1 - 0 , 001 = 0 , 504 0 , 999 = 504 999 = 56 111

Potom preložíme aj konečný desatinný zlomok do iného tvaru: 0, 56 = 56 100. Teraz máme dve čísla, s ktorými bude pre nás ľahké vykonať potrebné výpočty:

0 , (504) : 1 , 11 = 56 111: 56 100 = 56 111 100 56 = 100 111

Máme výsledok, ktorý vieme previesť aj na desatinné číslo. Ak to chcete urobiť, rozdeľte čitateľa menovateľom pomocou stĺpcovej metódy:

odpoveď: 0 , (504) : 0 , 56 = 0 , (900) .

Ak sme sa v príklade delenia stretli s neperiodickými desatinnými zlomkami, budeme postupovať trochu inak. Nedokážeme ich priviesť na bežné obyčajné zlomky, preto ich pri delení musíme najskôr zaokrúhliť na určitú cifru. Táto akcia sa musí vykonať s dividendou aj s deliteľom: v záujme presnosti zaokrúhlime aj existujúci konečný alebo periodický zlomok.

Príklad 3

Zistite, koľko bude 0, 779 ... / 1, 5602.

rozhodnutie

V prvom rade zaokrúhlime oba zlomky na stotiny. Takto prejdeme od nekonečných neopakujúcich sa zlomkov ku konečným desatinným miestam:

0 , 779 … ≈ 0 , 78

1 , 5602 ≈ 1 , 56

Môžeme pokračovať vo výpočtoch a získať približný výsledok: 0, 779 ...: 1, 5602 ≈ 0, 78: 1, 56 = 78100: 156100 = 78100 100156 = 78156 = 12 = 0,5.

Presnosť výsledku bude závisieť od stupňa zaokrúhľovania.

odpoveď: 0 , 779 … : 1 , 5602 ≈ 0 , 5 .

Ako deliť prirodzené číslo desatinnou čiarkou a naopak

Prístup k deleniu je v tomto prípade takmer rovnaký: konečné a periodické zlomky nahrádzame obyčajnými a nekonečné neperiodické zaokrúhľujeme. Začnime príkladom delenia prirodzeným číslom a desatinným zlomkom.

Príklad 4

Vydeľte 2,5 číslom 45.

rozhodnutie

Poďme 2, 5 do podoby obyčajnej frakcie: 255 10 \u003d 51 2. Ďalej to musíme rozdeliť na prirodzené číslo. Už vieme, ako na to:

25, 5: 45 = 51 2: 45 = 51 2 1 45 = 17 30

Ak výsledok preložíme do desiatkového zápisu, dostaneme 0 , 5 (6) .

odpoveď: 25 , 5: 45 = 0 , 5 (6) .

Metóda delenia stĺpcom je dobrá nielen pre prirodzené čísla. Analogicky to môžeme použiť aj pre zlomky. Nižšie uvádzame postupnosť akcií, ktoré je potrebné vykonať.

Definícia 1

Ak chcete rozdeliť stĺpec desatinných zlomkov prirodzenými číslami, musíte:

1. K desatinnému zlomku napravo pridajte niekoľko núl (na delenie ich môžeme pridať ľubovoľný počet).

2. Vydeľte desatinný zlomok prirodzeným číslom pomocou algoritmu. Keď sa delenie celočíselnej časti zlomku skončí, dáme do výsledného kvocientu čiarku a počítame ďalej.

Výsledkom takéhoto delenia môže byť buď konečný alebo nekonečný periodický desatinný zlomok. Závisí to od zvyšku: ak je nula, potom bude výsledok konečný, a ak sa zvyšky začnú opakovať, potom bude odpoveďou periodický zlomok.

Zoberme si niekoľko úloh ako príklad a skúsme tieto kroky doplniť konkrétnymi číslami.

Príklad 5

Vypočítajte koľko bude 65 , 14 4 .

rozhodnutie

Používame stĺpcovú metódu. Ak to chcete urobiť, pridajte k zlomku dve nuly a získate desatinný zlomok 65, 1400, ktorý sa bude rovnať originálu. Teraz napíšeme stĺpec na delenie 4:

Výsledné číslo bude výsledkom delenia celej časti, ktorú potrebujeme. Dáme čiarku, oddelíme ju a pokračujeme:

Dosiahli sme nulový zvyšok, preto je proces delenia ukončený.

odpoveď: 65 , 14: 4 = 16 , 285 .

Príklad 6

Vydeľte 164,5 číslom 27.

rozhodnutie

Najprv rozdelíme zlomkovú časť a dostaneme:

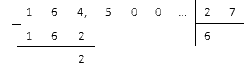
Výsledný údaj oddelíme čiarkou a pokračujeme v delení:

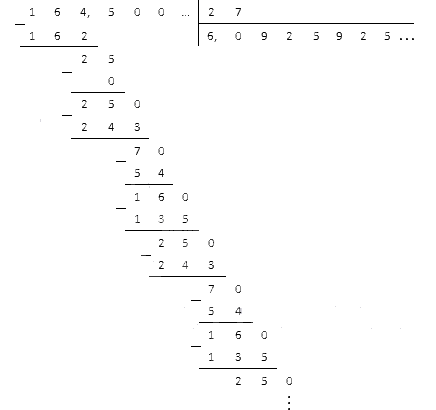
Vidíme, že zvyšky sa začali periodicky opakovať a čísla deväť, dva a päť sa začali v kvociente striedať. Tam sa zastavíme a odpoveď napíšeme ako periodický zlomok 6, 0 (925) .

odpoveď: 164 , 5: 27 = 6 , 0 (925) .

Takéto delenie možno zredukovať na proces hľadania súkromného desatinného zlomku a prirodzeného čísla, ktoré už bolo opísané vyššie. Aby sme to urobili, musíme vynásobiť deliteľa a deliteľa 10, 100 atď., aby sa deliteľ zmenil na prirodzené číslo. Potom vykonáme vyššie uvedenú postupnosť akcií. Tento prístup je možný vďaka vlastnostiam delenia a násobenia. V doslovnej forme sme ich napísali takto:

a: b = (a 10) : (b 10), a: b = (a 100) : (b 100) atď.

Formulujme pravidlo:

Definícia 2

Ak chcete rozdeliť jeden posledný desatinný zlomok druhým, musíte:

1. Posuňte čiarku v deliteľovi a deliteľovi doprava o počet znakov, ktoré sú potrebné na to, aby sa deliteľ zmenil na prirodzené číslo. Ak v dividende nie je dostatok znakov, na pravej strane k nej pridáme nuly.

2. Potom zlomok po stĺpci vydelíme výsledným prirodzeným číslom.

Poďme sa pozrieť na konkrétny problém.

Príklad 7

Vydeľte 7 287 2, 1.

Riešenie: Aby bol deliteľ prirodzeným číslom, musíme posunúť čiarku o jeden znak doprava. Prešli sme teda k deleniu desatinného zlomku 72, 87 číslom 21. Získané čísla si zapíšeme do stĺpca a vypočítajme

odpoveď: 7 , 287: 2 , 1 = 3 , 47

Príklad 8

Vypočítajte 16 , 3 0 , 021 .

rozhodnutie

Budeme musieť posunúť čiarku na tri číslice. Na to nie je dostatok čísel v deliteľovi, takže musíte použiť nuly navyše. Myslíme si, že konečný výsledok bude:

Vidíme periodické opakovanie zvyškov 4 , 19 , 1 , 10 , 16 , 13 . Kvocient sa opakuje 1, 9, 0, 4, 7 a 5. Potom je naším výsledkom periodické desatinné číslo 776 , (190476) .

odpoveď: 16 , 3: 0 , 021 = 776 , (190476) ​​​​​​

Nami popísaná metóda vám umožňuje urobiť opak, teda rozdeliť prirodzené číslo konečným desatinným zlomkom. Pozrime sa, ako sa to robí.

Príklad 9

Vypočítajte koľko bude 3 5 , 4 .

rozhodnutie

Je zrejmé, že budeme musieť posunúť čiarku doprava o jeden znak. Potom môžeme začať deliť 30, 0 číslom 54. Údaje zapíšeme do stĺpca a vypočítame výsledok:

Opakovaním zvyšku dostaneme číslo 0 , (5) , čo je periodické desatinné miesto.

odpoveď: 3: 5 , 4 = 0 , (5) .

Ako deliť desatinné miesta 1000, 100, 10 atď.

Podľa už preštudovaných pravidiel delenia obyčajných zlomkov je delenie zlomku na desiatky, stovky, tisíce podobné ako násobenie 1/1000, 1/100, 1/10 atď. Ukazuje sa, že na delenie , v tomto prípade stačí len presunúť čiarku na správne množstvočíslic. Ak v čísle nie je dostatok hodnôt na prenos, musíte pridať požadovaný počet núl.

Príklad 10

Takže 56, 21: 10 = 5, 621 a 0, 32: 100 000 = 0, 0000032.

V prípade nekonečných desatinných miest postupujeme rovnako.

Príklad 11

Napríklad 3 , (56) : 1 000 = 0 , 003 (56) a 593 , 374 ... : 100 = 5 , 93374 ... .

Ako deliť desatinné miesta 0,001, 0,01, 0,1 atď.

Rovnakým pravidlom môžeme zlomky deliť aj zadanými hodnotami. Táto akcia bude podobná násobeniu 1000 , 100 , 10 v tomto poradí. Aby sme to dosiahli, posunieme čiarku na jednu, dve alebo tri číslice v závislosti od podmienok problému a pridáme nuly, ak v čísle nie je dostatok číslic.

Príklad 12

Napríklad 5, 739: 0, 1 = 57, 39 a 0, 21: 0, 00001 = 21 000.

Toto pravidlo platí aj pre nekonečné desatinné miesta. Odporúčame vám len byť opatrní s periódou zlomku, ktorý je uvedený v odpovedi.

Takže, 7 , 5 (716) : 0 , 01 = 757 , (167) , pretože potom, čo sme posunuli čiarku v desiatkovom zápise 7 , 5716716716 ... dve číslice doprava, dostali sme 757 , 167167 ... .

Ak máme v príklade neperiodické zlomky, potom je všetko jednoduchšie: 394 , 38283 ... : 0 , 001 = 394382 , 83 ... .

Ako rozdeliť zmiešané číslo alebo spoločný zlomok desatinnou čiarkou a naopak

Tento úkon redukujeme aj na operácie s obyčajnými zlomkami. Ak to chcete urobiť, musíte ho vymeniť desatinné čísla zodpovedajúce obyčajné zlomky a zmiešané číslo zapíšte ako nevlastný zlomok.

Ak delíme neperiodický zlomok obyčajným alebo zmiešaným číslom, musíme to urobiť naopak, nahradiť spoločný zlomok alebo zmiešané číslo s príslušným desatinným zlomkom.

Ak si všimnete chybu v texte, zvýraznite ju a stlačte Ctrl+Enter

Nájdite prvú číslicu podielu (výsledok delenia). Ak to chcete urobiť, vydeľte prvú číslicu dividendy deliteľom. Výsledok zapíšte pod deliteľa.

• V našom príklade je prvá číslica dividendy 3. Vydeľte 3 12. Keďže 3 je menšie ako 12, výsledok delenia bude 0. Pod deliteľa napíšte 0 - toto je prvá číslica podielu.

Zvážte príklady delenia desatinných miest v tomto svetle.

Príklad.

Vydeľte desatinné číslo 1,2 desatinným číslom 0,48.

rozhodnutie.

odpoveď:

1,2:0,48=2,5 .

Príklad.

Periodickú desatinnú čiarku 0.(504) vydeľte desatinnou čiarkou 0,56 .

rozhodnutie.

Preložme periodický desatinný zlomok na obyčajný :. Konečný desatinný zlomok 0,56 preložíme aj na obyčajný, máme 0,56 \u003d 56/100. Teraz môžeme prejsť od delenia pôvodných desatinných miest k deleniu obyčajných zlomkov a dokončiť výpočty: .

Preložme výsledný obyčajný zlomok na desatinný zlomok vydelením čitateľa menovateľom v stĺpci:

odpoveď:

0,(504):0,56=0,(900) .

Princíp delenia nekonečných neperiodických desatinných zlomkov sa líši od princípu delenia konečných a periodických desatinných zlomkov, keďže neopakujúce sa desatinné zlomky nemožno previesť na obyčajné zlomky. Delenie nekonečných neperiodických desatinných zlomkov sa redukuje na delenie konečných desatinných zlomkov, pre ktoré sa vykonáva zaokrúhľovanie čísel do určitej úrovne. Okrem toho, ak je jedno z čísel, s ktorými sa delenie vykonáva, konečný alebo periodický desatinný zlomok, potom sa tiež zaokrúhli na rovnakú číslicu ako neperiodický desatinný zlomok.

Príklad.

Vydeľte nekonečné neopakujúce sa desatinné číslo 0,779... posledným desatinným číslom 1,5602.

rozhodnutie.

Najprv musíte zaokrúhliť desatinné zlomky, aby ste prešli od delenia nekonečného neopakujúceho sa desatinného zlomku k deleniu konečných desatinných zlomkov. Môžeme zaokrúhliť na stotiny: 0,779…≈0,78 a 1,5602≈1,56. Teda 0,779…:1,5602≈0,78:1,56= 78/100:156/100=78/100 100/156= 78/156=1/2=0,5 .

odpoveď:

0,779…:1,5602≈0,5 .

Delenie prirodzeného čísla desatinným zlomkom a naopak

Podstata prístupu k deleniu prirodzeného čísla desatinným zlomkom a k deleniu desatinného zlomku prirodzeným číslom sa nelíši od podstaty delenia desatinných zlomkov. To znamená, že konečné a periodické zlomky sú nahradené obyčajnými zlomkami a nekonečné neperiodické zlomky sú zaokrúhlené.

Pre ilustráciu si predstavte príklad delenia desatinného zlomku prirodzeným číslom.

Príklad.

Vydeľte desatinný zlomok 25,5 prirodzeným číslom 45.

rozhodnutie.

Nahradením desatinného zlomku 25,5 obyčajným zlomkom 255/10=51/2 sa delenie zredukuje na delenie obyčajného zlomku prirodzeným číslom: . Výsledný zlomok v desiatkovom zápise je 0,5(6) .

odpoveď:

25,5:45=0,5(6) .

Delenie desatinného zlomku prirodzeným číslom stĺpcom

Delenie konečných desatinných zlomkov prirodzenými číslami sa pohodlne vykonáva stĺpcom analogicky s delením stĺpcom prirodzených čísel. Tu je pravidlo rozdelenia.

Komu deliť desatinné číslo prirodzeným číslom stĺpcom, potrebné:

• pridajte niekoľko číslic vpravo v deliteľnom desatinnom zlomku 0, (počas delenia, ak je to potrebné, môžete pridať ľubovoľný počet núl, ale tieto nuly nemusia byť potrebné);
• vykonať delenie stĺpcom desatinného zlomku prirodzeným číslom podľa všetkých pravidiel pre delenie stĺpcom prirodzených čísel, ale keď je delenie celočíselnej časti desatinného zlomku dokončené, potom v súkromnom musíte dajte čiarku a pokračujte v delení.

Povedzme hneď, že delením konečného desatinného zlomku prirodzeným číslom možno získať buď konečný desatinný zlomok, alebo nekonečný periodický desatinný zlomok. Po rozdelení všetkých desatinných miest deliteľného zlomku iného ako 0 môžeme dostať buď zvyšok 0 a dostaneme konečný desatinný zlomok, alebo sa zvyšok začne periodicky opakovať a dostaneme periodické desatinné miesto zlomok.

Poďme sa pri riešení príkladov zaoberať všetkými zložitosťami delenia desatinných zlomkov na prirodzené čísla stĺpcom.

Príklad.

Vydeľte desatinné číslo 65,14 číslom 4 .

rozhodnutie.

Vykonajte delenie desatinného zlomku prirodzeným číslom stĺpcom. Pridajme dvojicu núl vpravo v zázname zlomku 65,14, pričom dostaneme desatinný zlomok rovný 65,1400 (pozri rovnaké a nerovnaké desatinné zlomky). Teraz môžete začať deliť celú časť desatinného zlomku 65,1400 prirodzeným číslom 4 stĺpcom:

Tým je delenie celočíselnej časti desatinného zlomku hotové. Tu v súkromí musíte zadať desatinnú čiarku a pokračovať v delení:

Dostali sme sa k zvyšku 0, v tejto fáze delenie stĺpcom končí. Vo výsledku máme 65,14:4=16,285.

odpoveď:

65,14:4=16,285 .

Príklad.

Vydeľte 164,5 číslom 27.

rozhodnutie.

Rozdeľme desatinný zlomok prirodzeným číslom stĺpcom. Po vydelení celočíselnej časti dostaneme nasledujúci obrázok:

Teraz dáme čiarku ako súkromnú a pokračujeme v delení stĺpcom:

Teraz je jasne vidieť, že zvyšky 25, 7 a 16 sa začali opakovať, zatiaľ čo čísla 9, 2 a 5 sa opakujú v kvociente. Takže vydelením desatinného čísla 164,5 číslom 27 dostaneme periodické desatinné číslo 6,0(925) .

odpoveď:

164,5:27=6,0(925) .

Delenie desatinných zlomkov stĺpcom

Delenie desatinného zlomku desatinným zlomkom možno zredukovať na delenie desatinného zlomku prirodzeným číslom stĺpcom. Aby ste to dosiahli, musíte dividendu a deliteľa vynásobiť takým číslom 10, alebo 100, alebo 1000 atď., aby sa deliteľ stal prirodzeným číslom, a potom vydeliť prirodzeným číslom stĺpcom. Môžeme to urobiť vďaka vlastnostiam delenia a násobenia, keďže a:b=(a 10):(b 10) , a:b=(a 100):(b 100) atď.

Inými slovami, deliť koncové desatinné miesto koncovým desatinným miestom, potrebujem:

• v delenci a deliteľovi posuňte čiarku doprava o toľko znakov, koľko je za desatinnou čiarkou v deliteľovi, ak zároveň v deleni nie je dostatok znakov na posunutie čiarky, tak treba pridať požadované množstvo nuly vpravo;
• potom vykonajte delenie stĺpcom desatinného zlomku prirodzeným číslom.

Zvážte pri riešení príkladu použitie tohto pravidla na delenie desatinným zlomkom.

Príklad.

Vykonajte rozdelenie stĺpca 7,287 na 2,1.

rozhodnutie.

Posuňme čiarku v týchto desatinných zlomkoch o jednu číslicu doprava, umožní nám to prejsť od delenia desatinného zlomku 7,287 desatinným zlomkom 2,1 k deleniu desatinného zlomku 72,87 prirodzeným číslom 21. Rozdeľme podľa stĺpca:

odpoveď:

7,287:2,1=3,47 .

Príklad.

Vydeľte desatinné číslo 16,3 desatinným číslom 0,021.

rozhodnutie.

Posuňte čiarku v dividende a deliteľovi doprava o 3 číslice. Je zrejmé, že v deliteľovi nie je dostatok číslic na to, aby niesol čiarku, preto pridajme požadovaný počet núl doprava. Teraz vydeľme stĺpec zlomku 16300,0 prirodzeným číslom 21:

Od tohto momentu sa začnú opakovať zvyšky 4, 19, 1, 10, 16 a 13, čo znamená, že sa budú opakovať aj čísla 1, 9, 0, 4, 7 a 6 v kvociente. Výsledkom je, že dostaneme periodický desatinný zlomok 776,(190476) .

odpoveď:

16,3:0,021=776,(190476) .

Všimnite si, že vyslovené pravidlo vám umožňuje deliť prirodzené číslo konečným desatinným zlomkom stĺpcom.

Príklad.

Vydeľte prirodzené číslo 3 desatinným zlomkom 5.4.

rozhodnutie.

Po posunutí čiarky o 1 číslicu doprava sa dostaneme k deleniu čísla 30,0 číslom 54. Rozdeľme podľa stĺpca:
.

Toto pravidlo možno použiť aj pri delení nekonečných desatinných zlomkov 10, 100, .... Napríklad 3,(56):1000=0,003(56) a 593,374…:100=5,93374… .

Delenie desatinných miest 0,1, 0,01, 0,001 atď.

Keďže 0,1 \u003d 1/10, 0,01 \u003d 1/100 atď., z pravidla delenia obyčajným zlomkom vyplýva, že delenie desatinného zlomku 0,1, 0,01, 0,001 atď. je to ako vynásobiť dané desatinné číslo 10 , 100 , 1000 atď. resp.

Inými slovami, ak chcete deliť desatinný zlomok 0,1, 0,01, ..., musíte posunúť čiarku doprava o 1, 2, 3, ... číslice, a ak nie je v desatinnom zlomku dostatok číslic, posuňte čiarku, potom je potrebné pridať požadované číslo k správnym nulám.

Napríklad 5,739:0,1=57,39 a 0,21:0,00001=21 000 .

Rovnaké pravidlo možno použiť pri delení nekonečných desatinných miest 0,1, 0,01, 0,001 atď. V tomto prípade by ste mali byť veľmi opatrní pri delení periodických zlomkov, aby ste sa nepomýlili s obdobím zlomku, ktorý sa získa v dôsledku delenia. Napríklad 7,5(716):0,01=757,(167) , keďže po posunutí čiarky v zázname desatinného zlomku 7,5716716716 ... dve číslice doprava máme záznam 757,167167 ... . S nekonečným počtom neperiodických desatinných miest je všetko jednoduchšie: 394,38283…:0,001=394382,83… .

Delenie zlomku alebo zmiešaného čísla desatinnou čiarkou a naopak

Delenie obyčajného zlomku alebo zmiešaného čísla konečným alebo periodickým desatinným zlomkom, ako aj delenie konečného alebo periodického desatinného zlomku obyčajným zlomkom alebo zmiešaným číslom sa redukuje na delenie obyčajných zlomkov. Za týmto účelom sú desatinné zlomky nahradené zodpovedajúcimi bežnými zlomkami a zmiešané číslo je reprezentované ako nesprávny zlomok.

Pri delení nekonečného neperiodického desatinného zlomku obyčajným zlomkom alebo zmiešaným číslom a naopak by sa malo pristúpiť k deleniu desatinných zlomkov, pričom obyčajný zlomok alebo zmiešané číslo sa nahradí zodpovedajúcim desatinným zlomkom.

Bibliografia.

• Matematika: štúdium. pre 5 buniek. všeobecné vzdelanie inštitúcie / N. Ya. Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartburd. - 21. vyd., vymazané. - M.: Mnemosyne, 2007. - 280 s.: chor. ISBN 5-346-00699-0.
• Matematika. 6. ročník: učebnica. pre všeobecné vzdelanie inštitúcie / [N. Ya, Vilenkin a ďalší]. - 22. vydanie, Rev. - M.: Mnemosyne, 2008. - 288 s.: chor. ISBN 978-5-346-00897-2.
• algebra: učebnica pre 8 buniek. všeobecné vzdelanie inštitúcie / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; vyd. S. A. Teljakovskij. - 16. vyd. - M. : Vzdelávanie, 2008. - 271 s. : chorý. - ISBN 978-5-09-019243-9.
• Gusev V. A., Mordkovich A. G. Matematika (príručka pre uchádzačov o štúdium na technických školách): Proc. príspevok.- M.; Vyššie škola, 1984.-351 s., ill.

V minulej lekcii sme sa naučili sčítať a odčítať desatinné zlomky (pozri lekciu „Sčítanie a odčítanie desatinných zlomkov“). Zároveň odhadli, o koľko sú výpočty zjednodušené v porovnaní s bežnými „dvojposchodovými“ zlomkami.

Žiaľ, pri násobení a delení desatinných zlomkov tento efekt nenastáva. V niektorých prípadoch desiatkový zápis dokonca tieto operácie komplikuje.

Najprv si predstavme novú definíciu. Stretneme sa s ním pomerne často a nielen v tejto lekcii.

Významnou časťou čísla je všetko medzi prvou a poslednou nenulovou číslicou vrátane upútavok. Hovoríme len o číslach, desatinná čiarka sa neberie do úvahy.

Číslice obsiahnuté vo významnej časti čísla sa nazývajú platné číslice. Môžu sa opakovať a dokonca sa rovnať nule.

Zvážte napríklad niekoľko desatinných zlomkov a zapíšte im zodpovedajúce významné časti:

1. 91,25 → 9125 (významné čísla: 9; 1; 2; 5);
2. 0,008241 → 8241 (významné čísla: 8; 2; 4; 1);
3. 15,0075 → 150075 (významné čísla: 1; 5; 0; 0; 7; 5);
4. 0,0304 → 304 (významné čísla: 3; 0; 4);
5. 3000 → 3 (významná postava len jeden: 3).

Upozornenie: nuly vo vnútri významnej časti čísla nikam nevedú. S niečím podobným sme sa už stretli, keď sme sa učili prevádzať desatinné zlomky na obyčajné (pozri lekciu “ Desatinné zlomky”).

Tento bod je taký dôležitý a chyby sa tu robia tak často, že v blízkej budúcnosti zverejním test na túto tému. Určite cvičte! A my, vyzbrojení konceptom významnej časti, v skutočnosti pristúpime k téme hodiny.

Desatinné násobenie

Operácia násobenia pozostáva z troch po sebe nasledujúcich krokov:

1. Pre každý zlomok zapíšte významnú časť. Získate dve obyčajné celé čísla - bez menovateľov a desatinných čiarok;
2. Vynásobte tieto čísla ľubovoľným pohodlný spôsob. Priamo, ak sú čísla malé, alebo v stĺpci. Získame významnú časť požadovaného zlomku;
3. Zistite, kde a o koľko číslic je posunutá desatinná čiarka v pôvodných zlomkoch, aby ste získali zodpovedajúcu významnú časť. Vykonajte spätné posuny na významnej časti získanej v predchádzajúcom kroku.

Ešte raz pripomeniem, že nuly po stranách významnej časti sa nikdy neberú do úvahy. Ignorovanie tohto pravidla vedie k chybám.

1. 0,28 ± 12,5;
2. 6,3 1,08;
3. 132,5 0,0034;
4. 0,0108 1600,5;
5. 5,25 10 000.

Pracujeme s prvým výrazom: 0,28 12,5.

1. Vypíšme významné časti pre čísla z tohto výrazu: 28 a 125;
2. Ich súčin: 28 125 = 3500;
3. V prvom multiplikátore sa desatinná čiarka posunie o 2 číslice doprava (0,28 → 28) a v druhom o ďalšiu 1 číslicu. Celkovo je potrebný posun doľava o tri číslice: 3 500 → 3 500 = 3,5.

Teraz sa poďme zaoberať výrazom 6.3 1.08.

1. Vypíšme podstatné časti: 63 a 108;
2. Ich súčin: 63 108 = 6804;
3. Opäť dva posuny doprava: o 2 a 1 číslicu. Celkovo - opäť 3 číslice doprava, takže spätný posun bude 3 číslice doľava: 6804 → 6.804. Tentoraz na konci nie sú žiadne nuly.

Dostali sme sa k tretiemu výrazu: 132,5 0,0034.

1. Významné časti: 1325 a 34;
2. Ich súčin: 1325 34 = 45 050;
3. V prvom zlomku sa desatinná čiarka posúva doprava o 1 číslicu a v druhom až o 4. Celkom: 5 doprava. Vykonávame posun o 5 doľava: 45050 → ,45050 = 0,4505. Nula bola na konci odstránená a pridaná dopredu, aby nezostala „holá“ desatinná čiarka.

Nasledujúci výraz: 0,0108 1600,5.

1. Píšeme významné časti: 108 a 16 005;
2. Vynásobíme ich: 108 16 005 = 1 728 540;
3. Počítame čísla za desatinnou čiarkou: v prvom čísle sú 4, v druhom - 1. Celkovo - opäť 5. Máme: 1 728 540 → 17,28540 = 17,2854. Na konci bola „extra“ nula odstránená.

nakoniec posledný výraz: 5,25 10 000.

1. Významné časti: 525 a 1;
2. Vynásobíme ich: 525 1 = 525;
3. Prvý zlomok je posunutý o 2 číslice doprava a druhý zlomok je posunutý o 4 číslice doľava (10 000 → 1 0000 = 1). Celkom 4 − 2 = 2 číslice vľavo. Prevedieme spätný posun o 2 číslice doprava: 525, → 52 500 (museli sme pridať nuly).

Všimnite si posledný príklad: odkedy sa desatinná čiarka presunie na rôznymi smermi, celkový posun sa zistí cez rozdiel. Toto je veľmi dôležitý bod! Tu je ďalší príklad:

Zoberme si čísla 1,5 a 12 500. Máme: 1,5 → 15 (posun o 1 doprava); 12 500 → 125 (posun 2 doľava). „Vykročíme“ o 1 číslicu doprava a potom o 2 číslice doľava. V dôsledku toho sme ustúpili 2 − 1 = 1 číslica doľava.

Desatinné delenie

Divízia je snáď najviac komplikovaná operácia. Samozrejme, tu môžete konať analogicky s násobením: rozdeliť významné časti a potom „presunúť“ desatinnú čiarku. Ale v tomto prípade existuje veľa jemností, ktoré negujú potenciálne úspory.

Pozrime sa teda na generický algoritmus, ktorý je o niečo dlhší, ale oveľa spoľahlivejší:

1. Preveďte všetky desatinné miesta na bežné zlomky. S trochou cviku vám tento krok zaberie pár sekúnd;
2. Rozdeľte výsledné frakcie klasickým spôsobom. Inými slovami, vynásobte prvý zlomok „prevrátenou“ sekundou (pozri lekciu „Násobenie a delenie číselných zlomkov“);
3. Ak je to možné, vráťte výsledok ako desatinné číslo. Aj tento krok je rýchly, pretože často má menovateľ už mocninu desať.

Úloha. Nájdite hodnotu výrazu:

1. 3,51: 3,9;
2. 1,47: 2,1;
3. 6,4: 25,6:
4. 0,0425: 2,5;
5. 0,25: 0,002.

Berieme do úvahy prvý výraz. Najprv preveďme zlomky obi na desatinné miesta:

To isté urobíme s druhým výrazom. Čitateľ prvého zlomku sa opäť rozloží na faktory:

V treťom a štvrtom príklade je dôležitý bod: po zbavení sa desatinného zápisu sa objavia zrušiteľné zlomky. Toto zníženie však nevykonáme.

Posledný príklad je zaujímavý, pretože čitateľ druhého zlomku je prvočíslo. Tu jednoducho nie je čo faktorizovať, takže to považujeme za „prázdne“:

Niekedy výsledkom delenia je celé číslo (hovorím o poslednom príklade). V tomto prípade sa tretí krok vôbec nevykoná.

Okrem toho sa pri delení často objavujú „škaredé“ zlomky, ktoré sa nedajú previesť na desatinné miesta. Tu sa delenie líši od násobenia, kde sú výsledky vždy vyjadrené v desatinnej forme. Samozrejme, v tomto prípade sa posledný krok opäť nevykoná.

Venujte pozornosť aj 3. a 4. príkladu. V nich zámerne neredukujeme obyčajné zlomky získané z desatinných miest. V opačnom prípade to skomplikuje inverzný problém - predstavuje konečnú odpoveď opäť v desiatkovej forme.

Pamätajte: základná vlastnosť zlomku (ako každé iné pravidlo v matematike) sama o sebe neznamená, že sa musí aplikovať všade a vždy, pri každej príležitosti.