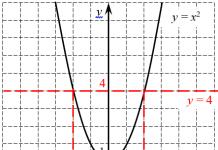
(Lab 2, layout with electronic integrator)

Objective:

1) familiarization with the functional elements of the PLL system and the principle of its operation;

2) study of accuracy depending on the structure and parameters of the system;

3) study of the possibilities of changing the dynamic properties of the system by the method of successive correction.

Description of the laboratory setup

The laboratory setup consists of a mock-up of the PLL system, a harmonic signal generator and an oscilloscope. The PLL system in the simplest configuration contains a phase discriminator (converts the phase difference of two signals into a control voltage), correction circuits and a controlled generator (a voltage-controlled reactive element is included in the timing circuit of this generator). If the input and output signals of the PLL system are detuned in phase (or frequency), then the phase discriminator generates a control voltage of the corresponding sign, under the action of which the parameters of the time-setting circuit of the controlled oscillator change and, accordingly, the frequency (and phase) of the output signal changes so as to reduce the initial detuning. Without taking into account the nonlinearity of the static characteristics of functional elements and the inertia of the phase discriminator, the transfer function of the PLL system in the open state can be represented as:

where is the transfer function of the corrective circuit; - gain.

In ACS of the 1st order of astatism, the dynamic tracking error depends on the rate of change of the impact (in our case, the phase) and the system gain:

(1)

where is the residual phase tracking error in degrees (it is useful to consider the phase as a dimensional quantity); – initial frequency detuning of generators [Hz].

There are 3 options for switching on the simplest PLL system (switch S1):

No correction (=1);

;

With sequential view correction: ,

moreover, the time constants of the correction circuits T 1 , T 2 and T 3 depend on the values ​​of the resistors and capacitances indicated on the layout.

The frequency and phase ratios of the signals of the controlled and external generators are observed from the Lissajous figures on the oscilloscope screen. To measure the tracking error, a phase shifter is used at the output of the controlled generator. Preliminarily set the "Detuning" knob of the external generator to position "0" and in the open state of the PLL system (position 1 of switch S1) perform manual coarse tuning of the frequency of the external generator according to the final result (Lissajous figure - ellipse). Then the tracking ring is closed and with the help of a phase shifter, the Lissajous figure is converted to a form convenient for observation (a line or a “figure of eight”). In the future, the frequency of the external generator is changed with the "Detuning" knob. A smooth change in the frequency of the input signal affects the tracking error, which leads to deformation of the Lissajous figure. By returning the figure to its previous position with the help of a phase shifter, it is possible to measure (on the scale of the phase shifter) the amount of residual error .

It should be borne in mind that the real dependence due to the non-linearity of the static (discriminatory) characteristics of the phase discriminator is described by a non-linear odd function. In this case, it is possible to experimentally obtain only a fragment of the dependence , on which a linear section should be identified to calculate the coefficient .

For a qualitative assessment of the speed and degree of oscillatory processes in the PLL system, a phase-shifting circuit is provided in the input signal circuit, which is switched on by the “Phase jump” toggle switch.

In a complete package, the PLL system contains, in addition, an electronic integrator: the "equivalent of the engine" is connected.

Job assignment

1. Turn on the generator, breadboard and oscilloscope.

2. Open the PLL (switch in position 1).

3. Set up the oscilloscope to observe Lissajous figures.

4. By changing the oscillator frequency, ensure that the frequencies of the external oscillator and the controlled oscillator of the PLL system coincide (an ellipse on the oscilloscope screen). Close the PLL (switch in position 2). Measure the PLL retention band.

5. Set the “generator frequency” knob to the middle position (see item 4). Using the phase shifter, fix the position of the ellipse, presenting it as a line or figure eight. By changing the frequency of the generator (“detuning” knob), and measuring the increment of the phase shift using a phase shifter, build a dependence (an odd function should be obtained). To build a graph, 3-5 points are required when the frequency is detuned in one direction and the same number of points in the other.

6. For the linear section of the dependence, determine the gain using formula (1). This value should be agreed with the teacher.

7. Using the obtained value, construct asymptotic logarithmic characteristics for 3 options for switching on the first-order PLL system of astatism (construct all LH on one graph for ease of comparison; the parameters of the corrective elements are indicated on the layout). By logarithmic characteristics, evaluate the quality of transient processes.

8. Qualitatively evaluate the transient processes in the PLL system (for this purpose, the “phase jump” toggle switch is used).

9. Turn on the “engine equivalent” and repeat steps 4-6 (when changing the generator frequency, take into account the long recharge of the electronic integrator capacitance). Sketch the electronic integrator circuit and calculate its transfer function (in general).

1. Functional diagram of the PLL system, diagrams of corrective elements indicating the values ​​of resistors and capacitances, electronic integrator circuit, open-loop system transfer functions for all studied options.

2. Table and graph of dependence, calculation and time constants of corrective elements.

3. Asymptotic LH for 3 options for constructing a PLL system of the first order of astatism.

4. Comparative characteristics of transient processes and their explanation.

5. Holding bands of the studied PLL systems.

6. The structure of the shaping filter for the situation Δf=const.

3.4. test questions

1. How do the functional elements of the PLL system and the whole system work?

2. What parameter of the input signal is informative for the PLL system?

3. What is the structure of the shaping filter in the case of Δf(t)=0, Δf(t)=const, Δf(t)=vt? What is the structure of the coordinated ACS?

4. How do the properties of the PLL system change with an increase (decrease) in the gain?

5. For what purpose are corrective elements included in the PLL system of the first order of astatism?

6. How do the properties of the PLL system change with an electronic integrator?

Searching the Internet for a device that matches the title of this article has been fruitless. The Forums believe that such a device cannot be created. However, at present, a prototype of a 16-bit ADC has been manufactured and tested on an ATmega 16 microcontroller (MC), which is part of a commercial product.

Circuit Description

Figure 1 shows the schematic diagram of the ADC, drawn in the Proteus 7.7 program. MK programming was done in IAR Embedded Workbench using the "Tutorial" author: Pashgan on the site The ADC operation was tested in hardware. Simulation of the ADC operation in Proteus did not work, the reason is described below.

Fig.1 Schematic diagram of a 16-bit ADC.

A detailed description of all elements (microcircuits) of the circuit can be found on the Internet, consider the purpose of each element in the ADC circuit.

Microcontroller ATmega 16

The diagram of the MK signals is shown in Figure 2. The MK must generate 2 clock signals of a fixed frequency of 122 Hz (16 MHz / 65536 = ~ 122 Hz). The timer-counter MK T1 operates in "normal mode", without a prescaler, with switching the state of the outputs OC1A and OC1B, and generates rectangular pulses on pins 18 and 19, of the "meander" type, which are shifted by 90 °. To do this, a number equal to half the maximum value of the T1 timer code is written to the OCR1B comparison register. At the output of the D4B chip (XOR logic element), rectangular pulses F1 of doubled frequency (244 Hz) are formed, which are fed to the first input (pin 14) of the Phase Detector (PD) of the Phase Locked Loop (PLL) D2 chip. The leading edge of the F1 pulses always coincides with the zero code of the timer T1. In a real circuit, due to delays in circuit elements, the initial offset of the zero code does not exceed 5 least significant bit units (EMP) of timer T1 and must be taken into account when generating the ADC conversion result. In the layout of the ADC, the delay in the MK is 2 EMP (0.125 μs) in 2 D4 elements - 3 EMP (0.15 μs)

Rice. 2. Diagram of MK signals and microcircuits D2 and D4.

If you set the “capture” mode of the T1 timer-counter state (“capture”) in the ATmtga 16 MK, and apply rectangular pulses with a frequency of 244 Hz to the ICP1 “capture” input, the leading edge of which will lag behind the leading edge of the F1 pulses in phase, then the 16-bit register ICR1 will read the 16-bit code of the phase shift between the leading edges of the pulses F1 and F0. The choice of symbols for the signals F1 and F0 is associated with the logic of the operation of the pulsed PD of the D2 74HC4046 chip. The leading edge of the F1 pulse sets the FD output (Tx pin 15 D2) to the state "Log.1", and the leading edge of the F0 pulse to the state "Log.0". In Proteus, pin 15 of the D2 chip "ZENER" is different from the "PHASE COMPARATOR III" in the chip's user manual. In the diagram of Figure 1, this error remained, because failed to fix graphic image of library item 74HC4046.

To solve the problem: to create a 16-bit ADC on an 8-bit AVR, you need a device that must convert an analog signal (for example, voltage) into the duration of Tx pulses (phase shift between pulses F1 and F0), the average voltage of which is equal to the input voltage Ux. This device is detailed in the PLL Stabilized Voltage to Pulse Width Converter article in the journal. Further in the description, the materials of this article will be used, which are necessary to explain the principle of operation of the ADC. To display the results of the ADC conversion, an alphanumeric LCD display TS1602-A, D5 in Figure 1 was used.

Chip 74HC4046 and operational amplifier ½ package D3 (AD823)

The 74NS4046 microcircuit and the operational amplifier (op-amp) form a PLL circuit, the input of which receives a pulse signal F1. The PLL is a Negative Feedback (NFO) automatic control system that adjusts the frequency of the internal Voltage Controlled Oscillator (VCO) so that its frequency Fo is equal to the frequency of the input signal F1, Figure 3. Adjustment is carried out due to the presence of negative feedback. The VCO output signal, a square wave of frequency F0, is compared on the Phase Detector (PD) with the input signal F1, the phase error signal after filtering and amplification is used to adjust the output frequency of the VCO.

Fig.3 Functional diagram of the PLL.

The PLL circuit is similar to the Operational Amplifier (OPA) circuit, with the only difference that the input variable is the phase of the oscillation, and the frequency (rate of phase change) is the feedback signal.

Rice. 4. Block diagram of the PLL.

Due to the fact that tuning is carried out according to the phase difference, the system is astatic with respect to frequency: in steady state, the tuning frequency is exactly equal to the frequency of the input signal (Fo=F1), and the phase shift is set so that the output voltage of the low-pass filter (Ugun) ensures frequency equality. Under certain conditions, which depend on the type of LPF, the PLL system can also be astatic in phase. A more detailed description of the PLL, with formula derivations, can be found on the Internet, and books,.

The PLL system is mainly used for frequency and phase modulation and demodulation, frequency multiplication and conversion, frequency filtering or reference waveform extraction for coherent signal detection. Typically, the input signal in PLL devices is the frequency. A PLL is a feedback loop control system in which the control parameters are the frequency or phase of the signal, and not the magnitude of its voltage or current. The proposed device uses a non-standard PLL switching circuit with an additional voltage regulation parameter.

Let us introduce into the standard PLL circuit the generator G of the signal F1 with a fixed frequency and the comparison element at the input of the low-pass filter, which should compare the input voltage Ux with the output signal of the PD. Let's change the shape of the functional diagram of the PLL. Figure 5 shows a functional diagram of the converter of the analog signal (voltage Ux) into the pulse duration Tx, Pulse Phase Modulation (PPM) with PLL.

Phase Modulation (PM) is one of the types of modulation of oscillations, where the phase of the carrier oscillation is controlled by an information signal (periodic change in the phase of oscillations according to a certain law; slow compared to the period of oscillations). From the definition of PM it follows that there is a sinusoidal signal generator, in which the phase of the output signal changes in time. This type of modulation is used in radio engineering to transmit information. PM is usually considered for sinusoidal signals.

Fig.5 Functional diagram of the converter of the analog signal Ux into the pulse duration Tx.

The proposed device uses phase modulation of pulse signals. If we apply a pulsed FD with a linear output characteristic, then we will get a precision voltage converter Ux into the pulse duration Tx. In this converter, the analog input signal Ux is compared with the output signal Tx (more precisely, the average value of the pulse Tx over the frequency period Fo (pulse area Tx) with the average value Ux over the same time). The presence of the OOS and a large gain (Ku) of the LPF provide high conversion accuracy and reduce the requirements for accuracy and stability of all circuit elements that are covered by the OOS. The hardware implementation of the proposed circuit is not a difficult task, many different PLL integrated circuits are currently being produced, for example, the CD4046 microcircuit (domestic analogues 1561GG1 and 564GG1) incorporates 2 types of PD, VCO and additional VCO control circuits. The 74HC4046 microcircuit, a functional analogue of the CD4046, has 3 types of PD and can operate at higher frequencies. Figure 6 shows the hardware implementation of a low-pass filter for negative input voltages.

Fig.6 LPF circuit for negative input voltages.

The low-pass filter is made according to the scheme of a Proportional-Integrating filter on the op-amp (PI filter), which compares the average values ​​of the Ux and Tx signals over the period of the frequency Fo, resistors R1 and R2 determine the scale factor of comparison. The product C1*R1 (the time constant of the integrator Ti) determines the integrating effect of the filter, the resistor R3 ensures the stability of the PIM circuit, and the ratio of R3 to R1 determines the proportional filter coefficient Kp. If the FD has an output characteristic in the region of positive voltages, then the input signal must have a negative polarity. If the input signal is positive, then it is necessary to use the differential circuit for switching on the op-amp (Fig. 7). The elements of the low-pass filter circuit must satisfy the following requirement: R3/R1 = R4/R2 and R1*C1 = R2*C2.

Fig.7 LPF circuit for positive input voltages.

The output signal of the low-pass filter controls the oscillator (VCO) so that the frequencies of the signals Fo and F1 are equal, and the phase shift between them is such that equality is satisfied.

Ux/R1 = (Up/R2)*Tx/T1, (1)

where Up is the amplitude of the pulse Tx (Up is the supply voltage of the FD);

T1 \u003d 1 / F1 frequency period at which the PLL operates.

The use of a PI filter makes the PLL system astatic in phase, which means that if R1 = R2, then the steady value of the relative duration of the output pulses of the converter (Tx / T1) is determined only by the ratio Ux / Up and does not depend on the parameters of other elements of the circuit.

Ux/Up = Тх/Т1, (2)

Ux = Up* Tx/T1. (3)

In formula (3), the known values ​​are the supply voltage of the FD (Up = 5v) and the period of the PLL frequency T1 = (1/16,000) * 65536 = 4.096 ms (the exact value of the frequency F1 = 244.140625 Hz). To measure the input voltage Ux, it is necessary to measure the pulse duration Tx (phase shift between the leading edges of the pulses F1 and F0) and substitute it in formula (3).

Method for calculating the elements of the PLL circuit

The initial parameter is the frequency F1, at which the ADC with PLL should operate. To calculate the dynamic characteristics of control systems, the circular frequency (angular frequency) ω = 2π*F, in [rad/s], phase dimension ⱷ in [rad] is used. In steady state, when the frequencies are F1=F0, the output characteristic of the PD (pin 15) of the D2 chip is shown in Figure 8.

Rice. 8 PD output characteristic.

FD conversion factor (pin 15 of D2 chip) Kfd = Up/2 π [V/rad].

The VCO, which is part of the D2 chip, has 2 ways (2 inputs, terminals 9 and 12) to control the output frequency F0:
- voltage control through the “VCON” input (pin 9), in addition to pin 11 “R1”, a resistor is connected, the choice of which is described in the manual for the use of the PLL chip;
- current control through the input ”R2” (pin 12), usually this input is used to set the initial frequency of the VCO in the absence of voltage to the input “VCON”.

In the diagram of Figure 1, the 2nd method of VCO frequency control is used, since in this case, a large range of low-pass filter output voltages is allowed, which is made on the D3A (AD823) op-amp chip. The output voltage of the op-amp, which can vary from -15V to +15V, is converted by resistor R5 into a VCO frequency control current. By selecting the values ​​of the circuit elements (C2, R4 and R5), the VCO is tuned in such a way that when the output voltage of the low-pass filter is zero (Ugun = 0 V), the output frequency of the VCO is Fo = 244Hz ± 10%, and with Vgun = minus 5V, the output frequency doubled Fo=488 Hz ±10%. This allows you to optimally use the entire linear range of the LPF output voltage to compensate for all non-linear characteristics of the circuit elements and maintain high ADC conversion accuracy.

Rice. 9 VCO output characteristic.

PLL Dynamics

For the competent use of the PLL, it is necessary to know the static and dynamic characteristics of this device. On the Internet, you can find a detailed derivation of the PLL transfer function for different versions of the LPF. Figure 10 shows a block diagram of a linear model of an ADC with a PLL in steady state when, after power-up, the transient (searching and locking frequency F1) ended F0 = F1. The transfer functions of the circuit elements are presented in operator form.

Rice. 10 Block diagram of a linear model of an ADC with a PLL in steady state.

Let's use the ready formula for the transfer function W(p) (a mathematical description of the behavior of a dynamic system) of the PLL, in which the PI filter is applied. The transfer function (4) corresponds to the oscillatory link of the 2nd order:

where p is a complex variable that can be replaced by jω to build the device's AFC;

ωп = 2π*Fп is the natural circular frequency of the PLL bandwidth in [rad/s];

Fп – natural frequency of the PLL bandwidth in [Hz] (transient frequency of the PLL loop);

ξ is the damping factor (attenuation of the transient process) of the PLL.

Figure 11 shows the logarithmic frequency response of the PLL in relative units of natural frequency for different values ​​of the attenuation coefficient ξ. Additionally, expressions are given that connect the parameters of the PLL transfer function with the parameters of the devices included in the analog signal converter circuit into the pulse duration.

where Kfd is the constant of the PD transfer coefficient (V/rad);

Kgun - VCO gain constant (rad/s*V);
Ti = R1*C1 – PI filter integrator time constant (c);
Кп = R3/R1 is the proportional coefficient of the PI filter;

Fig.11 Logarithmic frequency response of the 2nd order link.

The PLL frequency response corresponds to a 2nd order low-pass filter with a cutoff frequency ωp (rad/s) (transient frequency) and a slope (attenuation) of 20 dB per decade (6 dB/octave). When designing a converter with a PLL, it is necessary to choose the bandwidth of the device ωp=2π*Fp and the damping (attenuation) coefficient ξ at frequencies above the cutoff frequency.

Let us determine the calculated parameters of a real ADC with a PLL, which is shown in Figure 1.

Let's write down the parameters of the elements of a real converter with a PLL in literal terms (see Fig. 8 and Fig. 9): Kfd = Ur/2π; Kgun = 2πF0/Up; Ti = 1/F0 and F0= F1. We substitute the literal values ​​of the parameters into formulas (5) and (6), we obtain simple (for engineering evaluation) formulas for calculating the dynamic characteristics of the PLL converter.

ωp = F0 [rad/s], (7)

Fп = F0/2π [Hz], (8)

ξ = Кп/2. (nine)

Substitute in formulas (8) and (9) the values ​​of a real converter with a PLL, we obtain the following values:

PLL converter bandwidth Fp = 244Hz/6.28 = 39Hz;
- damping coefficient ξ = 1/2 = 0.5.

Using formulas (5) and (6), it is possible to achieve the desired characteristics of the input signal conversion transient by changing the parameters of the circuit elements and the conversion frequency F0.

ADC layout test results with ATmega 16

To check the accuracy of converting the input voltage Ux of the ADC with a PLL, a V7-38 voltmeter was used, which displays the measured voltage with 5 decimal places with an error of no worse than 0.05% at the limit of 2V, with a resolution of 0.1mV and no worse than 0.1% at limit of 20V with a resolution of 1mV.

The ADC layout with PLL has a measurement limit of ~ 6.5V (6553.5mV), the measured voltage is displayed on the LCD display (D5) with 5 decimal places with a resolution of 0.1mV. The choice of the measurement limit is associated with the maximum decimal number 65535, which corresponds to the maximum value of the binary code of the timer-counter T1. The reference voltage source of the ADC is the supply voltage of the D2 chip (74HC4046), which in the breadboard is Up = 5.029V (5029.0 mV) (measured by B7-38). In order for the EMP code of the timer-counter T1 to be 0.1mV, condition (1) must be met, the maximum input current Uxmax /R1 must be balanced by the current of the feedback circuit Up/R2 (10).

65536 / R1 = 50290 / R2, (10)

R1 = R2* (65536/50290),

R1 \u003d 1.303 * R2,

R1 \u003d 130.3 kOhm (see Fig. 1).

The circuit in Figure 1 shows a variable resistor RV1 = 1kΩ, which is connected in series with R1 = 130kΩ to fine-tune the ADC conversion scale factor. Table 1 and Figure 12 show the results of measuring the input voltage Ux using an ADC breadboard with a PLL and a V7-38 voltmeter. The voltage Ux [V] was set from a laboratory power supply with a built-in voltmeter. In the 1st, 2nd and 3rd columns of Table 1, the readings of voltmeters are given without taking into account the sign (modulo) to simplify the comparison of the readings of Ux, B7-38 and ADC. In the 5th reading of the LCD display of the ADC, and in the 4th reading of the ADC, in which an error of 5 EMP is excluded, associated with the initial offset of the front pulse F1 relative to the zero code of the timer T1. In the 6th and 7th columns of Table 1, the values ​​of the relative measurement errors in [%] of the voltmeter of the power supply relative to V7-38 and the ADC readings relative to V7-38, respectively. In the LCD display, there is no comma after the 4th digit, which should appear after the completion of the MK program.

Table 1.

Fig.12 Graphical representation of the results of testing the ADC with PLL.

In the attachment to the letter there is a file "Photo ATsPF.xlsx" with photographs, which simultaneously record the readings of V7-38 and ADC with PLL. The video clip about the experiment has a large amount of memory and can be transferred to the editorial office if there is a request.

Analyzing ADC Design Test Results with ATmega 16

The results of checking the layout of the ADC show that the deviation of the ADC readings from the readings of the V7-38 reference device does not exceed 0.02%. This indicates a high linearity of the conversion of the input voltage into the pulse duration using the PLL.

The resolution of the ADC, when measuring voltages of more than 2 Volts, is 10 times higher than that of the V7-38 voltmeter (0.1mV for the ADC and 1mV for the V7-38 voltmeter).

The stability of the ADC readings does not exceed ±EMP, which indicates the low level of intrinsic noise of the voltage-to-pulse duration conversion method using the PLL.
In reality, in the ADC circuit with a PLL, two signals of different shapes are compared, a constant voltage and rectangular pulses, which can be represented as the sum of a constant voltage Up / 2 and an infinite series of sinusoidal voltages ( Trigonometric Fourier series), the amplitude of which depends on the pulse duration Tx, and the frequency multiples of the ADC conversion frequency (F1).
The filtering properties of the PLL are described in detail in the literature. The PLL is an ideal noise trap with frequencies that are multiples of the frequency at which the ADC operates. If the input signal Ux contains interference with frequencies F1, 2 F1, 3F1, etc., then they will be completely suppressed, because the average voltage (integral) of these sinusoids over the frequency period F1 is zero. The transfer function (11) of such a filter is shown in Fig.13.

Fig.13 Frequency response of the filter (11).

(11)

This unique feature of the PLL is due to the integrating property of the VCO, whose output frequency is determined by the average voltage over the operating frequency F1. Therefore, it is possible to compare at the input of the low-pass filter 2 different-shaped signals, a constant voltage Ux with a pulse signal Tx, while the noise in the pulse duration Tx is determined by interference with frequencies that are not a multiple of the operating frequency of the PLL. Considering that all internal processes of the MC and ADC are synchronized with the frequency of the MC crystal oscillator, the impulse noise generated by the operation of the MC does not affect the stability of the ADC readings. Therefore, a PLL ADC provides a resolution of 16 binary (5 decimal) bits. The resolution of the ADC built into the MK case is 10 binary (3 decimal) digits, the real stability of readings is 8 digits, which is 2 orders of magnitude worse than that of the ADC with PLL.

Limitations that exist in ADC with PLL, and how to overcome them

The PD of the PLL chip (74NS4046) in the Frequency Detector (FR) mode, when the VCO is synchronized (frequency lock F1=F0), has an output characteristic in accordance with Figure 14.

Fig.14 Output characteristic of 74NS4046 (pin 15) in BH mode.

When the power is turned on (during the transient process), it is possible to synchronize the PLL circuit on the subharmonics of the operating frequency, for example, F0 = 1.5*F1. Synchronization on the subharmonics of the operating frequency occurs when the input signal Ux is on the border of the linear range of the PD output characteristic (Ux = ~ 0 or Ux = ~ Up).To eliminate such synchronization, the output characteristic of the PD in the frequency comparison mode must have a relay characteristic in accordance with Figure 15. In the phase comparison mode, it must correspond to Figure 8.

Fig.15 Output, relay characteristic of PD for ADC with PLL in frequency comparison mode F1 and F0.

Ready-made PD microcircuits with such a characteristic are not yet produced, so you can use the relay PD circuit, which was developed by the author and is given in the appendix to the article.

The second limitation is related to the operation of the voltage converter Ux into the pulse duration Tx, code Ux=0V or Ux=Uр. The output characteristic of the PD (Figure 8) has a periodic character with a period of 2π, so it is necessary to reduce (for example, by 2%) the input voltage range in relation to the supply voltage of the PD [(Ux)max = 0.95Up] and shift the origin of the pulse duration, for example , by 1% (see Fig.16). When displaying the result of the ADC conversion using the program, take into account these changes in the output characteristic of the PD.

Fig.16 ADC working area on the PD output characteristic when F1= F0.

Conclusion

The non-standard use of the PLL and MC system (without built-in ADC) made it possible to create a cheap and precision ADC with high resolution and low intrinsic noise.

Limit values ​​for speed and resolution of ADC with PLL depend on the type of microcontroller.

If the ADC with PLL will be widely used by developers of electronic devices, then I suggest the abbreviated name "ADPC".

The ADTF is an ideal trap filter for interference that is present in the input signal Ux if the interference frequency is equal to or a multiple of the operating frequency of the converter F1 (2F1, 3F1, etc.). If you synchronize the operating frequency of the MK with a network frequency of 50 Hz (using an RF oscillator, a divider and another PLL system), then interference in the input signal Ux at frequencies multiple of 50 Hz will be suppressed, and the stability of the readings will increase.

Given that the ATsF is an ideal noise suppression filter, you can use this device to convert the output signal to a digital code, for example, an inductive sensor with a Phase-Sensitive Rectifier (PV) at the output. Typically, a low-pass filter is used to smooth out the ripple of the PV output voltage to the level of the required resolution of the ADC. This introduces a large delay in the signal control system. If you apply the ADCF at the frequency F1 = Fmod, where Fmod is the modulation frequency (power supply of the inductive sensor), then a low-pass filter is not required, its function will be performed by the ADCF device itself.

State of the art FPGA (Programmable Logic Integrated Circuit) technology is ideal for building ADPCs in a single package.

The first application of the ATsP, but without a microcontroller, which did not exist 30 years ago, was used by the author to transmit analog signals with high accuracy through the optocoupler decoupling of the telemetry channels of the satellite equipment. An attempt to obtain an Author's Certificate for this technical solution was unsuccessful. The application for the Author's Certificate may still be in the State Public Library for Science and Technology.

History reference

The principle of phase locked loop (synchronization) operates in nature everywhere. Synchronization was discovered by Huygens in the middle of the 17th century (1650 - 1680), who observed the adjustment of the periods of clocks hanging on one wall. The use of Phase Locked Loop (PLL) in electronic devices began in 1932, when the Frenchman H. de Belsize first described a synchronous signal reception scheme that was simpler and more elegant than the superheterodyne reception scheme used at that time. This PLL circuit in Figure 17, in which a feedback signal causes a voltage-controlled oscillator to tune exactly to the frequency of the incoming signal, is widely used in many modern information processing and communication devices.

http://www.dsplib.ru/content/pll/pll.html http://physics.nad.ru/Physics/Cyrillic/harm_txt.htm
10. http://www.kit-e.ru/articles/elcomp/2003_8_92.php
11. Blekhman I.I. Synchronization in nature and technology.
12. "Electronics: past, present, future" (Translated from English under the editorship of Corresponding Member of the Academy of Sciences of the USSR V.I. Siforov ["Mir"; M.; 1980 (296 p.)].

PLL (Phase Locked Loop), as its name implies, is an automatic control system (following system), the tuning frequency of which is determined by the frequency of the control signal, and the error signal is the phase difference between the control signal and the feedback signal. Due to the fact that tuning is carried out according to the phase difference, the system is astatic with respect to frequency: in steady state, the tuning frequency is exactly equal to the frequency of the control signal. Under certain conditions, the PLL system can be astatic and out of phase.

Along with the main property of auto-tuning, the PLL system has the property of filtering and behaves, regardless of its functional purpose, like a tracking polynomial filter. The PLL system is a system with multifunctional capabilities and is used for frequency modulation and demodulation, frequency filtering (including filtering the frequency modulating function), frequency multiplication and conversion, selection of the reference wave for coherent detection, etc.

The PLL system can be analog, pulse, digital, or a combination (analog-pulse, pulse-digital, and so on). In an analog PLL system, a continuous signal operates, characterized by the instantaneous values ​​of the parameters at each moment in time. In an impulse system, signal parameters are characterized by discrete values, which can be instantaneous or interval. A pulse signal with instantaneous readings is, for example, a rectangular (meander type) signal of a controlled generator, characterized by instantaneous frequency values ​​at the points of level change. A pulse with interval readings is, for example, a signal of a pulsed phase detector (PD), the pulse duration of which is determined by the measured phase interval. An interval pulse signal can cause temporal and other types of distortion. In a digital PLL system, respectively, a digital signal is used, which is a discrete data stream determined by the values ​​of quantized samples of the analog signal and expressed in a digital code. Quantized readings of a digital signal can also be both instantaneous and interval.

The following is a generalized engineering analysis of a PLL system with analog and pulse elements and considers the applications of the system.

The considered PLL systems are widely used in microelectronic components manufactured by well-known companies. For example, Analog Devices uses a PLL system:

• in one- and two-channel synthesizers ADF410x/1x/5x and ADF420x/1x/5x types “Integer-N” and “Fractional-N” with programmable (tunable) frequencies up to 3.7 GHz;
• for clock multiplication in TxDAC+ AD9751/3/5 (300 MHz), AD9772/4 (400/128 MHz) DACs, in AD9852/4 (300 MHz) digital synthesizer-modulators (DDS) and AD9853/6 modulators (168 /200 MHz);
• to multiply the frequency by k = 2 N /n times, where n is an integer from the series 1, 2, ... 2 N /2.5, - with AD9850/1/2/4 DDS synthesizers as frequency dividers in feedback loops (for example, with N = 48 and a maximum frequency after multiplication of 300 MHz using the AD9852);
• as a frequency modulator combined with a frequency synthesizer and a frequency demodulator combined with a frequency converter - in the AD6411 transceiver chip of the DECT system;
• as a quadrature modulator combined with a quadrature frequency converter - in the AD6523 transceiver chip used in conjunction with the AD6524 synthesizer (also based on a PLL), - in GSM and DCS systems;
• as a reference frequency source with quadrature output for the demodulator in the AD6432 GSM transceiver chip.

Texas Instruments uses the system:

• in two- and three-channel frequency synthesizers TRF2020 - up to 0.25, 0.25 and 1.2 GHz, TRF2050 - up to 0.25 and 1.2 GHz, TRF2052 - up to 0.15 and 2.0 MHz and TRF3040, which is also a modulator, - up to 0.2 and 2.0 GHz;
• for the synthesis of reference frequency signals for modulators in TRF3040 and TRF3520 microcircuits;
• for clock multiplication in TMS320C54x, TMS320C62x, TMS320C67x and TMS320VC33 digital signal processors.

Motorola (Semiconductor Product Sector) uses the system in two-channel frequency synthesizers MC145181 (up to 550 and 60 MHz), MC145225 (up to 1.2 and 0.55 GHz), MC145230 (up to 2.2 and 0.55 GHz), etc. intended for radio communication equipment of various systems.

Gran-Jansen AS (Norway) uses a PLL system in the GJRF400 (GJRF10) transceiver operating in the 300–500 MHz frequency range for reference waveform synthesis and for analog frequency modulation.

The above list is far from complete, however, the listed microcircuits quite fully characterize the possibilities of using the PLL system.

Basic ratios

In a generalized form, any automatic control system, regardless of its purpose, contains a measuring device with a subtractor at the input and a control object, the output of which is connected to the subtractor. The subtractor compares the control variable and the control variable (from the output of the regulated object), which is the feedback value. Along with the concepts of control and controlled quantities, we will use the concepts of input and output, which determine the functional purpose of the system. In the general case, the input and output quantities are not always control and controlled (in the indicated understanding of these terms). Transfer function of the system -

K (p) \u003d x out / x in \u003d K pr (p) /, (1)

where x out and x in are the output and input values, and K pr (p) and K arr (p) are the transfer functions of the direct transmission circuits (from input to output) and negative feedback (from output to input), p is the operator Laplace (a plus sign in the denominator means that the feedback is negative). The input value can be fed to the input of any element, and the output value can also be taken from the output of any element of the system.

Rice. one

On fig. Figure 1a shows a diagram of the simplest PLL system containing a PD phase detector (measuring device), a PD filter, and a controllable VG generator (regulated object). PD and VG are mandatory elements of the system, and the filter that affects its dynamic (frequency) properties may be absent. The control variable is the frequency w 0 + D w in the alternating voltage at the input of the FD, the components of which are: w 0 - the reference frequency of the system and D w in - the change in frequency, which is the input value that affects the system. The feedback value is the CG frequency equal to w 0 + D w arr, where D w arr = D w in – pD j , and pD j and D j are changes in frequency and phase at the PD input caused by D w in. On fig. 1b shows a diagram of a variant of the system, which differs in that only the reference frequency w 0 acts at the PD input, and the input value of the system is the voltage uin at the input of the CG applied through the “+” adder. Input and output values ​​D w in and u out in fig. 1a determine the purpose of the system - a frequency demodulator, and u in and w 0 + D w out in fig. 1b - frequency modulator. Functionally, the adder in fig. 1b is a subtractor, since negative feedback acts in the system loop.

Despite the fact that the control variable in the PLL system is the frequency, in the PD, it is not the frequencies that are compared, but the phases of the voltages at its input. As a result, the phase difference, which is the integral of the frequency difference, is equal to D j = (D w in - D w arr) / p (Fig. 1a) or D j = -D w out / p (Fig. 1b), and the transfer function PD, respectively, K PD (p) = K PD /p, where K PD is the transmission coefficient with the dimension V / rad. The phase difference at the input of the PD, in addition to D j , may contain the initial constant component j 0, at which at the input of the PD j = j 0 + D j . The component j 0 is the integration constant and is determined by the choice of the PLL system mode, taking into account the detector characteristic of the PD.

The transfer function of the PLL system according to the scheme in Fig. 1a used for frequency demodulation is characterized by the expression

K BH (p) \u003d U out / D w in \u003d K 0 /, (2)

where u out - voltage at the filter output (output voltage of the demodulator), due to a change in frequency at the input D w in, K 0 = 1/K UG - system transfer coefficient (in this case, at “zero” frequency), t 0 = 1 /K PD K Ф K SG - “intrinsic” (without taking into account k Ф (p) filter) time constant of the system, K SG - transfer coefficient of the controlled generator (with the dimension (rad/s)/V), and K Ф and k Ф (p) - constant and frequency-dependent factors of the transfer function of the filter K Ф (p) = K Ф k Ф (p). In the absence of a filter, that is, with K Ф (p) = 1,

K BH (p) \u003d K 0 / (1 + pt 0), (3)

where t 0 = 1/K FD K CG. The transfer function (3) is a function of a polynomial LPF of the 1st order. In general, the order of the PLL system is equal to one plus the order of the applied filter Ф (integrating circuit or LPF).

Transfer functions (2) and (3) are “external” functions of the PLL system, determined by the given input and output of the system. The main function of the system is

K D j (p) = D j /D w in = /, (4)

where D j is the change in the phase difference at the input of the PD, due to a change in the control frequency D w in, and 1 + pt 0 /k Ф (p) in the denominator of the function is a polynomial of the system (according to the terminology in the theory of polynomial filtering), present in all “external ” transfer functions, including those in (2), differing in expressions in the numerator.

Elements of the PLL system

As already mentioned, the main (mandatory) elements of the PLL system are PD and VG, which in the systems under consideration can be analog or pulse. In addition, the considered PLL systems can include analog filters, frequency dividers with pulse or analog outputs, mixers, etc.

Phase detectors. On fig. Table 2 shows the detector characteristics of the most used FDs:

• sinusoidal characteristic of phase detection of multiplying and switching analog amplitude-phase detectors (APD) (Fig. 2a);
• sawtooth characteristic of the trigger pulse PD (Fig. 2b);
• triangular characteristic of the multiplying pulsed PD (Fig. 2c) (its variant is also shown in Fig. 2d);
• sawtooth characteristic of the phase detection of a bipolar trigger pulse frequency-phase detector (PFD) (Fig. 2e).

Rice. 2

First of all, we note that the detector characteristics are static, in which the dynamic error inherent in pulsed FDs does not manifest itself. In analog PDs, the instantaneous phase difference is measured

D j (t) = j 1 (t) - j 0 (t) = d j (t),

where, in the simplest case, j 1 (t) = w 0 t + d j (t) and d j (t) is the phase and modulating phase change of the detected signal, and j 0 (t) = w 0 t is the phase of the reference oscillation. We emphasize that we are talking about the current difference between the instantaneous values ​​j 1 (t) and j 0 (t), simultaneously counted at the same time t.

In pulsed FDs, unlike analog ones, the phase interval D j (D t i ) is measured, which is proportional to the time interval D t i = t 0i – t i , where t 0i and t i are different moments of time at which the phases of the signal j 1 (t i) = w 0 t i + d j (t i) and the reference oscillation j 0 (t 0i) = w 0 t 0i are equal. Usually, points are taken with zero instantaneous values ​​of the sinusoid (Fig. 3a), which ensure the formation of input and, accordingly, output pulses of the PD, shown in Fig. 3a. 3b-d. When j 1 (t i) and j 0 (t 0i) are equal, the time interval is D t i = d j (t i) / w 0, and the phase interval is

D d (D t i) = w 0 D t i = d j (t i), (5)

According to (5), the measured phase intervals D j (D t i) are numerically equal to the desired instantaneous phase differences d j (t i). However, it should be taken into account that in the current time scale the sequence of interval readings is equivalent to the sequence of instantaneous readings at discrete points t j = t i + D t i /2 - instead of points t i , to which they correspond. As a result, the phase will be measured with a time error D t i /2:

D j (t i) = d j (t i + D t i /2)

Let us consider the detector characteristics of the PD. The multiplier analog NPD characteristic shown in fig. 2a is determined by the expression

U NPD = K NPD Ucosj, (6)

where U is the amplitude of the detected voltage, j is the phase difference between the detected and reference voltages, and K NPD is the detection coefficient depending on the amplitude of the reference voltage, which must therefore be constant. Both voltages, detected and reference, are sinusoidal. Expression (6) is also valid for a switching analog NPD using a detectable sinusoidal voltage switch controlled by a square-wave reference voltage. In the general case, the analog APD, according to (6), detects not only the phase difference, but also the amplitude of the detected voltage U, which is why it is called amplitude-phase. In accordance with the foregoing, during phase detection, the amplitude of not only the reference, but also the detected voltage should be maintained constant. The dependence of u NPD on U is a disadvantage of the detector if it is used as a phase detector (a switching NPD can also be used as a synchronous amplitude detector). Another drawback of the analog NPD is the non-linearity of its characteristics, and therefore its narrow sections are used for detection, for example, from p /4 to 3p /4 or from -3p /4 to -p /4. With the introduction of a phase shift j 0 = -p /2, the operating point on the APD characteristic (Fig. 2a) shifts to the left by the specified angle, and the argument j in (6) is replaced by a detected phase change D j . As a result,

U NPD = K NPD UsinD j = K NPD UD j, (7)

where the second (approximate) part of the expression, proportional to D j , is for the portion of the phase range D j from -p /4 to p /4.

Note that the analog multiplier, which has the above disadvantages (when used as a phase detector), is widely used as a mixer in frequency converters, where a high “purity” of the converted frequency spectrum is required, and for which analog multipliers are ideal elements.

As a multiplying pulsed PD with the characteristic in Fig. 2c (inverse with respect to the characteristic in Fig. 2a), the XOR microcircuit is usually used, however, it has unstable output levels “0” and “1”, and therefore it is of little use for direct measurement of the phase difference. Therefore, an analog multiplexer with a two-bit address input is used as PD inputs. Such a multiplexer can be represented as consisting of an XOR phase-detecting microcircuit and an output switch controlled by it. The use of a commutator and switched accurate voltages ensures accurate characteristics of the PD. In addition, depending on the choice of levels of switched voltages, it is possible to change the value of the conversion (detection) coefficient, as well as the vertical shift of the characteristic and its inversion. On fig. 2d shows a shifted characteristic due to the switching voltages -E and E (instead of 0 and 2E, which corresponds to the characteristic in Fig. 2c). In addition, the characteristic in Fig. 2d is shown as a function of D j for j 0 = p /2 (similarly to (7) for APD):

U PD = K PD D j, (8)

Characteristic (8) is linear in the operating range from -p /2 to p /2.

Multiplying pulsed PDs are widely used in PLL systems. Let us note the following features in the operation of PDs: in pulsed PDs, constant levels of “foreign” sources are switched, while in switched analog NPDs, the detected voltage is switched. And besides, in pulsed FDs, the switch is controlled by pulses from the output of the multiplier, while in analog NPDs, the switch is controlled by a reference voltage.

The characteristic of a trigger pulsed PD, for example, of the RS-trigger type (Fig. 2b), differs from the considered characteristics by a twice as large phase range, from 0 to 2p, and the slope of the working section of the characteristic of only one sign, positive or negative (the positive slope of the characteristic shown in Fig. 2b). Fig. 2b, can be changed to negative by “polarity reversal” of trigger inputs or outputs). To improve the accuracy of the characteristic, like the XOR, a switch with switched accurate voltages can be switched on at the trigger output. It is essential that the considered FD is a trigger and works “along the front”, while multiplying FDs work “by duration”. For this reason, the trigger (trigger) PD has less noise immunity, and, in addition, its use leads to transients at the beginning of demodulated bursts. The phase response of the FPD is a combination of two characteristics of the trigger pulsed PD, added with opposite signs (Fig. 2e). In modern PFDs, widely used in frequency synthesizers, measures have been taken to ensure high-quality “crosslinking” of two characteristics, in which the detection noise is practically absent (the so-called low-noise PFDs). The phase range of the PFD is from -2p to 2p. The polarity of the PFD output pulses is determined by the sign, and the duration, as in a conventional trigger FD, is determined by the value of the measured phase difference (phase interval). Typically, PFDs have a current output (with a high output resistance), which is convenient when building systems with passive proportional-integrating circuits as a filter. In steady state, when using a PLL with phase astatism, the duration of the pulses at the PFD output is zero (there are no pulses). This mode is the main one when using FFD in frequency synthesizers. With frequency detuning, the PFD operates as a frequency detector with a bipolar relay detection characteristic that depends on the detuning sign.

Rice. 3

The characteristics of PDs of all types are periodic, which is due to the periodicity of the change in the phase angle. The positive or negative slopes of the analog or multiplying pulse PD characteristics determine the plus or minus sign of the PD transfer function, which is automatically selected by the PLL when it is turned on. At the same time, negative feedback is provided in the system, taking into account the signs (plus or minus) of the transmission coefficients of other elements. In contrast to the sinusoidal or triangular PD characteristics, the sawtooth characteristics of the trigger PD and PFD require a preliminary selection of the sign of the slope, which, as mentioned above, can be changed by “reversing the polarity”.

Usually, a PD, as well as a detector of any kind, is understood as an element consisting of two parts - detecting and filtering. When constructing a PLL system, its first detecting part is used as a PD, and the applied filter is considered as an element of the system. The output signal of the PD contains a useful component that is proportional or almost proportional (depending on the type of PD) to the detected phase difference, as well as high-frequency components that appear as ripples and are usually subject to filtering. The ripple spectrum is determined by the carrier with frequency doubling (for multiplying FDs and switching FD with doubling) or without frequency doubling (for switching FD without doubling and trigger FDs).

In addition to the above, we note that the input signals of the analog and multiplying pulse PDs must be respectively sinusoidal or rectangular with a duty cycle equal to 2. For trigger PDs, the duty cycle is not required, but it should be borne in mind that the phase difference between the edges of the pulses that trigger and trigger reset.

controlled generators. As already mentioned, the VG in the PLL system can be analog or pulsed (as well as PD). An analog VG can be a narrow-band high-frequency (hundreds of MHz, units of GHz) transistor generator with an oscillatory circuit, which uses voltage-controlled varicaps (varactors). The generator does not require the offset E0 shown in fig. 1a, b. Its mode is provided by its own bias circuit. The output voltage of the generator is sinusoidal, but when using a comparator it can be rectangular (pulsed).

As a pulsed UG (with a frequency of up to units of MHz), a broadband voltage-to-frequency converter with continuous integration and charge balancing, also known as a PFM modulator, can be used. The frequency of such a VG (its instantaneous discrete values) is proportional to the converted analog voltage (its instantaneous values ​​at the same time reference points). An example of the considered UG can be the AD650 and AD654 converters from Analog Devices. There is a type of UG with synchronization of the output signal frequency by clock pulses (AD652, AD7741/2). Such a VG is similar to a sigma-delta modulator and is intended for use in systems with digital conversion.

Rice. 4

On fig. 4a shows a block diagram of a pulsed CG (without synchronization), and in fig. 4b - diagrams of stresses on its elements. The voltages on the elements of the filterless PLL system with the considered pulsed CG and multiplying pulsed PD are also shown there. On fig. 4a,b: Uin - voltage at the control input of the PD; U arr is the feedback voltage at the other input of the PD, which is the output voltage of the HS (U HS); U vkhUG - voltage at the input of the UG, which is the output voltage of the PD (U PD); U int, U comp and U one - the voltage of the integrator, comparator and single vibrator as part of the UG. The voltage diagrams clearly illustrate the operation of the VG and the PLL system as a whole. It can be seen, in particular, that UvkhUG is “filtered” in the integrator;

Frequency dividers. Frequency dividers included in the feedback loop between the VG and PD provide frequency multiplication by the PLL at the VG output. Ordinary counters or specially designed dividers for frequency synthesizers (in combination with counters switched on at the PLL input) can be used as dividers. In frequency synthesizers, fractional frequency multiplication is provided with high resolution, implemented by software tuning. Special frequency dividers used in synthesizers include “Integer-N” and “Fractional-N” dividers (with integer and fractional division factors, respectively). The first of them are widely used in frequency synthesizers, the second are new, providing higher parameters of synthesizers. The digital (DDS) synthesizers mentioned above with an analog output can also be used as frequency dividers.

Typically, devices using the PLL system are available as microcircuits in a single chip. External filters are considered below, as well as frequency-setting circuits of controlled generators containing inductive elements, capacitors and varicaps (varactors).

PLL operation mode

Rice. 5

On fig. Figure 5a shows a diagram of the PLL system (in a simplified form without a filter) with the designation of values ​​characterizing the operating mode of the system (for an amplifier, such a mode would be called a DC mode). On fig. 5a, the control variable is the frequency w0 at the input, which, due to the phase-locked loop, is equal to the frequency of the CG, and the control voltage of the CG and, accordingly, the output voltage of the PD are equal to E 0 = w 0 /K CG. The initial phase difference at the PD input with the characteristic in fig. 2c (multiplying pulsed PD with switched voltages 0 and 2E) is equal to j 0 = E 0 /K PD = w 0 /K PD K UG = w 0 t 0 . Usually j 0 = p /2 or -p /2 is chosen, at which the operating point is in the middle of the linear section of the characteristic.

On fig. Figure 5b shows a variant of the circuit with an external bias source E0, corresponding to the circuit in fig. 1c. In this variant, the voltage at the PD output is equal to zero, but the initial phase, as in the previous case, is equal to j 0 = p /2 or -p /2. The latter is provided by switching voltages PD, equal to -E and E, and corresponds to the characteristic in fig. 2y. In reality, in the diagrams in Fig. 5a,b, the initial phase difference and the output voltage of the PD will have insignificant deviations from the indicated values, which is due to the auto-tuning of the system to compensate for the influence of deviations in the parameters of the PD and VG and the voltage E0 of the external source from the specified nominal values.

Despite the complication, the circuit in Fig. 5b (Fig. 1c) may be more preferable for the following reason. The fact is that the time constant t 0 determines, along with k Ф (p), the dynamic properties of the system, and therefore it should be possible to choose its required value. At the same time, for the circuit in Fig. 5a, according to the above expression for j 0 , the values ​​t 0 and j 0 are interconnected, and changing t 0 will entail changing j 0 . As a result, the set PD mode and the PLL system as a whole will change. The scheme in fig. 5b does not have this drawback, and t 0 can be chosen independently of j 0.

Frequency properties of the PLL system

The transfer function (3) is a 1st order function. Applying a filter to a PLL changes the dynamic properties of the system. The polynomial of the system (the polynomial in the denominator of the transfer functions) determines the order, the type of approximation and the frequency range of the filtering, and the term or polynomial in the numerator determines the type of filtering (low-pass, high-pass or band-pass filtering) and the transfer coefficient.

Rice. 6

2nd order PLL systems typically use one of the 1st order filters shown in Fig. 6 (note that the generally accepted name “filter” in this case is conditional; it would be more correct to consider them as frequency correction circuits):

• integrating filter (IF) (Fig. 6a) with transfer function K Ф (p) = U out /U in = 1/(1+p t Ф) = k Ф (p) at K Ф = 1, where t Ф = RC - filter time constant;
• proportional-integrating filters (PIF) (Fig. 6b,c) with transfer function K Ф (p) = U out /U in = (1 + p t Ф1)/(1 + p t Ф) = k Ф (p) at K Ф = 1, where t Ф = RC, t Ф1 = R2C, R = R1 + R2;
• proportionally integrating circuits (PI) (Fig. 6d,e) with transfer function K Ф (p) = U out / I in = K Ф k Ф (p), where K Ф = R, k Ф (p) = 1 + 1/p t Ф1 , t Ф1 = RC.

The PI circuit differs from the IF and PIF in that the source of its input signal is a current source I in with infinitely high resistance. In the PLL system, the PI circuit is implemented, for example, using an operational amplifier with PI as a parallel negative feedback circuit. The transfer function of the circuit with the amplifier is K Ф (p) = -(K Ф + 1/p t Ф) = -K Ф k Ф (p), where K Ф = R/r, t Ф = rC, r is the current-setting resistance of the circuit , included at the input of the amplifier, and k Ф (p) - according to PI in fig. 6g, d. The minus sign, determined by the inverting inclusion of the amplifier, must be taken into account in the phasing of the PD, if the PD is with a sawtooth characteristic. Note that tФ is the “physical” time constant of the PI circuit, as well as the PIF, while t Ф1 is a conditional time constant, convenient for writing mathematical expressions. The transfer function of the PI, determined by K Ф + 1/p t Ф, unlike the PIF, consists of two functions - proportional to KФ and integrating 1/p t Ф. K Ф affects the quality factor and, accordingly, the stability of the system (at KФ --> 0 the PLL system is unstable), and the term 1/p t Ф determines the integrating property of the PI, which ensures the astatism of the PLL system with respect to the phase. Recently, instead of an operational amplifier that provides current “powering” of the PI, a current shaper is used, which is used together with the PFD considered above. The specified shaper provides the connection of the PI with the “lower” output to the “ground”. Note that, along with the simplest RC circuit in Fig. 6d, chains of complex configuration and, accordingly, higher orders are used as PIs.

In addition to the main filter outputs U out, connected in the PLL system to the input of the HS, in fig. 6b-d shows additional outputs U out * , which, along with the main ones, can be used to pick up the output signal of the PLL system. Using additional outputs is equivalent to connecting external filters at the output of the system that are not used in a closed feedback loop. The transfer functions of the filters for additional outputs, along with those for the main outputs, are shown in the table.

The polynomial of the transfer functions of the 2nd order PLL system, as well as polynomial filters of the same order, is determined by the generalized expression 1 + p / w 0 Q + p 2 / w 0 2 , where w 0 is the natural frequency of the system, known in filter theory as the frequency poles, and Q - quality factor, which determines the type of approximation of frequency characteristics (according to Butterworth, Chebyshev, etc.). The table shows the polynomials of the PLL functions with different filters, as well as the corresponding expressions Q and w 0 . The table also shows the data of the main function K D j (p) (4) and the transfer function of the system when it is used as a frequency demodulator: K BH ^ (p) - with output after the PD (before the filter), K BH (p) - after filter and KCHD * (p) - when removing the signal from the additional output of the filter. We emphasize that the operator p in the transfer functions of the PLL system is determined by the expression jW , where W is the frequency of the frequency change at the input and, accordingly, the output voltage (with frequency modulation, this is the modulation frequency).

Analyzing the data given in the table, we can draw the following conclusions. The function K D j (p) of the 1st order PLL is a function of the LPF, and with PI - a function of the PF (bandpass filtering) with a resonant frequency w 0 . The PF function of the PI system determines the astatism of the system with respect to the phase: the gain at zero frequency is zero. The transfer function K D j (p) of the system with IF and PIF is the total function of the LPF and PF, which can be considered as a function of the LPF, changed in the region of the cutoff frequency. Recall that 2nd order filtering is low-pass filtering if the numerator of the function is a zero-order term (t 0), and band-pass filtering is first-order filtering (pt 0 t Ф1).

The functions K BH (p) and K BH* (p) for the system with PIF are identical to the functions for the system with PI, but they are achieved with the different K D j (p) indicated above. The use of additional outputs, characterized by K BH* (p), provides, in contrast to K BH (p), obtaining transfer functions of the LPF type (Fig. 6b, d) and PF (Fig. 6c, e), and K BH * ( p) LPF type is similar to KCHD(p) of the system with IF. A feature of the use of the PIF, in comparison with the IF, is that the required quality factor can be set by changing the ratio R2/R (t Ф1 /t 0) without changing t 0 and t Ф and, accordingly, without changing w 0 .

Application of the PLL

The use of the PLL system is related to which of its elements is the input and which is the output. Consider the main applications of the PLL system.

frequency demodulator. When using the PLL system as a frequency demodulator, the FM signal is fed to the PD input (Fig. 1a, c), and the demodulated signal is taken, for example, from the filter output. The transfer function of the demodulator will be determined by the expressions for the numerator and denominator given in the table, as well as expression (2). To filter the demodulated signal with the required parameters, an additional external filter is usually used. In this case, the PLL system should be considered as the first stage of filtering and should be taken into account accordingly when calculating the overall filter transfer function (with the required order, approximation and cutoff frequency).

frequency modulator. When using the PLL system as a frequency modulator, the modulating signal uin(t) is applied to the input of the CG, as shown in Fig. 1b, and modulated - is removed from the output of the UG. In this case, the modulator itself is the VG, and the PLL system sets the carrier frequency, which is determined by the reference (control) frequency at the PD input. In addition, the system provides filtering of the modulated signal, determined by the selected parameters of the transfer function. In general terms, the transfer function of the PLL in FM mode, in contrast to (2) for demodulation,

To FM (p) \u003d D w out / u in \u003d,

where K 0 = t 0 K When using a mutual fund

K FM (p) \u003d (pK 0 + p 2 K 0 t f) / (1 + pt 0 + p 2 t 0 t f); (9)

K FM * (p) \u003d pK 0 / (1 + pt 0 + p 2 t 0 t f), (10)

Accordingly, to pick up the FM signal from the main and additional outputs of the PIF (Fig. 6b). Function (9) is the total function of the PF and HPF, and function (10) is the function of the PF. The second signal pickup option is more preferable for narrowband modulated signals.

Rice. 7

frequency filters. On fig. 7a shows a diagram of a PLL system with frequency filtering of the voltage uin, and in fig. 7b - with frequency filtering of the modulating frequency change Dwin as part of the FM signal. Both filters have the same transfer function

K f (p) = 1/,

which is a function of the LPF when using the IF and the total function of the LPF and PF - when using the PIF and PI. In addition, the first of the filters (Fig. 7a) can be used with the signal pickup from the additional outputs of the PIF and PI, for which the LPF and PF functions are respectively implemented.

Phase shifter. The dependence of the constant phase difference at the PD input on the operating mode of the PLL system is shown above (Fig. 5a,b). In accordance with this, when picking up a signal from the output of the UG, as shown in Fig. 7b, it is possible to obtain a phase shift of the output signal, for example, j 0 = p /2 or -p /2 (quadrature phase shift). The angle j 0 = p /2 is provided by choosing the PD characteristic in Fig. 2d, and j 0 = -p /2 - with “polarity reversal”, for example, sources E and -E. Other angles are also possible.

Frequency multiplier. Frequency multiplication by the PLL is achieved by including a “:N” frequency divider in the feedback loop as shown in fig. 7th century The frequency at the output of the VG, which is the output of the multiplier, is equal to w out \u003d w 0 N, where N is the division factor of the divider. In frequency synthesizers, at the input of the PLL, a frequency divider “:R” is additionally included (not shown in Fig. 7c). As a result, w 0 = w in /R, and w out = w in N/R, where R is the division factor of the divider “:R”. The combined use of dividers ":R" and ":N" (with programmable division ratios) provides frequency synthesis in a wide range and with high resolution.

The introduction of a frequency divider into the feedback circuit increases the inertia of the PLL: t 0 = N/K PD K F K UG. The inertia can be reduced by introducing an additional gain that will compensate for the influence of N, but there is another way. In frequency synthesizers, as indicated above, frequency dividers of the “Integer-N” or “Fractional-N” type are used. The latter, unlike the former, is characterized by fractional numbers of the coefficient N. Therefore, the values ​​of N for “Fractional-N” can be smaller (for example, N = 10.25 instead of 1025 for “Integer-N”) with a correspondingly larger (in the same 100 times) w 0 . With a smaller value of N, there will be a smaller effect on t 0 , and with a correspondingly larger value of w 0, the conditions for filtering the PD signal at the input of the HS are facilitated.

Frequency multiplication can also be implemented in a PLL system with a DDS synthesizer as a frequency divider, but at lower frequencies. If for the ADF4113 synthesizer (with “Integer-N”) the synthesized frequencies are up to 3.7 GHz, then for the frequency multiplier with the AD9852 DDS synthesizer it is up to 300 MHz. Frequency multiplication is sometimes combined with frequency modulation (keying), as, for example, in the AD6411 transceiver chip. Note that when multiplying the frequency of the FM signal, not only the frequency of the carrier wave is multiplied, but also the frequency deviation.

Rice. eight

Frequency conversion with phase locked loop. On fig. Figure 8a shows a diagram of a PLL system with a built-in frequency converter containing an “X” mixer and a BPF bandpass filter tuned to a frequency difference w 0 = w 1 – w 2 (AD6411 chip). The input value is w 1 + D w in with carrier w 1, and the output is the voltage u out. The device in question is a frequency demodulator in which demodulation is preceded by frequency conversion. A feature of the device, in contrast to the usual inclusion of a converter and a demodulator (without feedback), is that it auto-tunes the system to the difference frequency w 0 . It is set as a control variable at the PD input.

The device under consideration can be used not only for demodulation, but also for frequency conversion, without removing the demodulation signal. In this case, w 2 is the converted carrier, and the signal is taken from the output of the CG, as shown in Fig. 8b. The transfer function of the demodulator in fig. 8a

K BH (p) \u003d K 0 /, (11)

where k Ф (p) and k PF (p) are variable multipliers of transfer functions Ф and PF, and K 0 = 1/K UG. In the simplest case, if the PF is second order with k PF (p) = ap/(1 + ap + bp 2),

K BH (p) \u003d K 0 /

is the LPF function, the order of which is reduced by one due to the multiplier ap in the numerator of the PF function. The expression for the transfer function of the converter is the same as for the demodulator, but with K0 = 1.

Quadrature modulation with phase lock. On fig. 8c shows a diagram of a PLL-based quadrature modulator used in GSM and DCS radio communication systems (AD6523 chip). The loop of the PLL system shows a quadrature modulator “Mod.”, at the input of which is a frequency converter “X”. The transfer function of the modulator in fig. 8c

K mod (p) = D w out / u in = K mod /, (12)

where K mod \u003d D w mod / u in - modulator gain “Mod.”. If there is band pass filtering in the system, it is additionally taken into account in (12) like (11).

We note the following interesting fact. In the systems in Fig. 8, mixers and a modulator are used, which are signal multipliers and, accordingly, are non-linear elements (as, indeed, a phase detector). But for the frequencies and phases of the same signals, they are adders or subtractors. As a result, the mixer and modulator are linear elements for changing the frequency.

The application of the PLL system is not limited to the examples given. Any system whose operation is based on phase locked loop is, accordingly, a PLL system in one form or another. The components of the manufacturers listed above are typical examples of the application of the PLL system. Components that use the PLL system are diverse and feature high specifications.

Literature

1. Phase Locking Systems with Discretization Elements / Ed. V.V. Shahgildyan. - M.: Radio and communications. - 1989.
2. Fomin A.A. and other Analog and digital synchronous-phase meters and demodulators. - M.: Radio and communications. - 1987.
3. Levin V.A. and others. Frequency synthesizers with a system of pulse-phase self-tuning. - M.: Radio and communications. - 1989.
4. Curtin M., O'Brien P. Phase Locked Loops for High-Frequency Receivers and Transmitters // Analog Dialogue, Analog Devices, 1999, Vol. 33, no. 3, 5, 7.
5. Fague D. OthelloTM: A New Direct-Conversion Radio Chip Set Eliminates IF Stages // Analog Dialogue, Analog Devices, 1999, Vol. 33, no. ten.
6. Golub V. GJRF10 transceiver from Gran Jansen AS // Chip News. - 1998. - No. 4. - S. 30–32.
7. Moshits G., Horn P. Design of active filters. - M.: Mir. - 1984.
8. Golub V.S. Instantaneous and average frequency of oscillations and integrating FM and PFM modulators // Radio engineering. - 1982. - v. 37. - No. 9. - S. 48–50.
9. Golub V. A look at the sigma-delta ADC // Chip News. - 1999. - No. 5. - S. 23–27 (as amended in No. 8, p. 48).
10. Technical Brief SWRA029: Fractional/Integer-N PLL Basics / C.Barrett. - Texas Instruments, August 1999.
11. Golub V.S. Equivalent circuit of the PLL system // Izv. universities. Radioelectronics. - 1994. - v. 37. - No. 8. - S. 54–58.

Phase-Locked Loop (PLL) is a very important and useful unit, produced as a separate integrated circuit by many manufacturers. A PLL contains a phase detector, an amplifier and a voltage controlled oscillator (VCO), and is a combination of analog and digital technology in one package. Let us further consider the use of PLL for tone decoding, demodulation of AM and FM signals, frequency multiplication, frequency synthesis, pulse synchronization of signals from noisy sources (for example, magnetic tape) and restoration of "clean" signals.

There is a traditional prejudice against PLLs, partly due to the difficulty of implementing a PLL on discrete components, and partly due to doubts about its reliable operation.

Rice. 9.67. Phase locked loop circuit.

With the advent of inexpensive and easy-to-use PLLs, the first barrier to their widespread use has been overcome. When properly designed and used correctly, PLLs become as reliable circuit elements as op-amps or flip-flops.

On fig. Figure 9.67 shows a classic PLL. A phase detector is a device that compares two input frequencies and generates an output signal proportional to their phase difference (if, for example, the frequencies differ, then a periodic signal at the difference frequency will appear at the output). If not equal to , then the filtered and amplified phase error signal will affect the frequency of the VCO, changing it in the direction of . Under normal conditions, the VCO quickly “locks” to the frequency, maintaining a constant phase shift with respect to the input signal.

Since the filtered output of the phase detector is a DC signal and the driving input is a VCO measure of the input frequency, it is clear that the PLL can be used for FM detection and tone decoding (used in digital transmission over telephone lines). The VCO output is a local frequency signal, so the VCO outputs a clean reference signal that may contain noise. Since the VCO output signal can be of any shape (triangular, sinusoidal, etc.), this allows you to form, say, a sinusoidal signal, synchronized with the input pulse train.

In one common application, a PLL is connected between the VCO output and the phase detector with a modulo counter, thus providing a multiplication of the input frequency reference. This is an ideal method of generating clock pulses at multiples of the mains frequency for integrating ADCs (two-stage and charge-balancing) with complete rejection of mains frequency noise and its harmonics. Such circuits are the main ones in the construction of frequency synthesizers.

PLL components.

The simplest phase detector is the type 1 (digital) detector, which is a simple XOR gate (Figure 9.68). The figure shows the dependence of the output voltage on the phase difference when using a low-pass filter and a rectangular input waveform with a duty cycle of 50%. The type 1 (linear) phase detector has a similar output voltage versus phase difference, although its circuitry is a "four-quadrant multiplier", also known as a "balanced mixer". Highly linear phase detectors of this type are widely used in synchronous detection, which we consider in Sec. 15.15.

The type 2 phase detector is sensitive only to the location of the edges of the signal and the input VCO, as shown in fig. 9.69.

Rice. 9.68. Phase detector (type 1), made according to the XOR scheme.

The phase comparator circuit generates either lag or lead output pulses depending on when logic transitions of the VCO output signal occur, after or before reference signal transitions, respectively. The width of these pulses is equal to the time interval between the corresponding edges, as shown in the figure. During the action of these pulses, the output circuit either diverts or gives out current, and in the intervals between pulses it is in an open state, forming the relationship between the output voltage and the phase difference shown in Fig. 9.70. The process is completely independent of the duty cycle of the input pulses, in contrast to the situation with the type 1 phase comparator discussed earlier. Another attractive feature of this phase detector is that the output pulses completely disappear when the two signals are synchronized. This means that there is no "ripple" at the output that causes periodic phase modulation in the loop, as is the case with a type 1 phase detector.

Rice. 9.69. Phase detector (type 2) lead-lag, working "on the fronts".

Let us compare the properties of two main types of phase detectors:

There is another difference between these two types of phase detectors. The type 1 detector always generates an output waveform which must then be filtered by a control loop filter (more on this later). Thus, the Type 1 phase detector PLL contains a loop filter that acts as a low pass filter to smooth the full amplitude logic output. In such a circuit, there is always some residual ripple and hence periodic phase changes. In circuits where the PLL is used for frequency multiplication or synthesis, “phase modulation sidebands” are added to the output signal (see Section 13.18).

The type 2 phase detector, on the other hand, generates output pulses only when there is a phase difference between the reference signal and the VCO signal. Since the output of the phase detector would otherwise appear as an open circuit, the loop filter capacitor acts as a voltage storage element, maintaining a voltage that maintains the desired VCO frequency. If the reference signal “droops” in frequency, then the phase detector generates a series of short pulses, charging (or discharging) the capacitor to the new voltage needed to bring the VCO back into synchronism.

Voltage controlled generators. An important component of the PLL is the oscillator, whose frequency can be controlled using the output of the phase detector. Some PLL ICs contain a VCO (such as the 565 line element and the 4046 CMOS element). In addition, there are separate VCO ICs listed in Table. 5.4. An interesting class of VCOs are sine output elements (8038, 2206, etc.) because they allow you to generate a pure sine wave, synchronized with the input waveform of a "scary" type. Another class of VCOs worth mentioning are voltage to frequency, which are usually designed for optimal linearity; they have, as a rule, a modest maximum frequency (up to 1 MHz) and generate pulses with logic levels (see Section 5.15).

Keep in mind that the frequency of the VCO is not limited by the speed of the logic circuits. You can, for example, use radio frequency generators tuned using a varactor (diode with variable capacitance) (Fig. 9.71).

Taking this idea one step further, one could even use an element such as a reflective klystron, a microwave (gigahertz) generator, electrically tuned by varying the voltage across the reflector. Of course, a PLL using such oscillators would require an RF phase detector.

The frequency versus voltage response of a PLL VCO may not be highly linear, but if it is highly non-linear, the gain in the loop will vary with the frequency of the signal and more stability will need to be maintained.