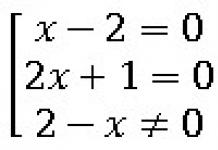Proyecto educativo "ecuaciones en tareas OGE". Resolver ecuaciones cuadráticas Resolveré ecuaciones cuadráticas antiguas.

Las ecuaciones cuadráticas se estudian en octavo grado, por lo que aquí no hay nada complicado. La capacidad de resolverlos es absolutamente necesaria.

Una ecuación cuadrática es una ecuación de la forma ax 2 + bx + c = 0, donde los coeficientes a, byc son números arbitrarios y a ≠ 0.

Antes de estudiar métodos de solución específicos, tenga en cuenta que todas las ecuaciones cuadráticas se pueden dividir en tres clases:

No tener raíces;
Tener exactamente una raíz;
Tienen dos raíces diferentes.

Esta es una diferencia importante entre ecuaciones cuadráticas y lineales, donde la raíz siempre existe y es única. ¿Cómo determinar cuántas raíces tiene una ecuación? Hay algo maravilloso para esto. discriminante.

discriminante

Sea la ecuación cuadrática ax 2 + bx + c = 0. Entonces el discriminante es simplemente el número D = b 2 − 4ac.

Necesitas saber esta fórmula de memoria. De dónde viene no es importante ahora. Otra cosa es importante: por el signo del discriminante se puede determinar cuántas raíces tiene una ecuación cuadrática. A saber:

Si D< 0, корней нет;
Si D = 0, hay exactamente una raíz;
Si D > 0, habrá dos raíces.

Tenga en cuenta: el discriminante indica el número de raíces, y no sus signos, como por alguna razón mucha gente cree. Echa un vistazo a los ejemplos y lo entenderás todo tú mismo:

Tarea. ¿Cuántas raíces tienen las ecuaciones cuadráticas?

x2 − 8x + 12 = 0;

5x 2 + 3x + 7 = 0;

x 2 − 6x + 9 = 0.

Escribamos los coeficientes de la primera ecuación y encontremos el discriminante:
a = 1, segundo = −8, c = 12;
re = (−8) 2 − 4 1 12 = 64 − 48 = 16

Entonces el discriminante es positivo, entonces la ecuación tiene dos raíces diferentes. Analizamos la segunda ecuación de manera similar:
a = 5; segundo = 3; c = 7;
re = 3 2 − 4 5 7 = 9 − 140 = −131.

El discriminante es negativo, no hay raíces. La última ecuación que queda es:
a = 1; segundo = −6; c = 9;
re = (−6) 2 − 4 1 9 = 36 − 36 = 0.

El discriminante es cero; la raíz será uno.

Tenga en cuenta que se han escrito coeficientes para cada ecuación. Sí, es largo, sí, es tedioso, pero no mezclarás las probabilidades ni cometerás errores estúpidos. Elija usted mismo: velocidad o calidad.

Por cierto, si lo dominas, después de un tiempo no necesitarás anotar todos los coeficientes. Realizarás tales operaciones en tu cabeza. La mayoría de la gente empieza a hacer esto después de 50-70 ecuaciones resueltas; en general, no tanto.

Raíces de una ecuación cuadrática

Pasemos ahora a la solución en sí. Si el discriminante D > 0, las raíces se pueden encontrar usando las fórmulas:

Fórmula básica para las raíces de una ecuación cuadrática.

Cuando D = 0, puedes usar cualquiera de estas fórmulas; obtendrás el mismo número, que será la respuesta. Finalmente, si D< 0, корней нет — ничего считать не надо.

x 2 − 2x − 3 = 0;

15 − 2x − x 2 = 0;

x2 + 12x + 36 = 0.

Primera ecuación:
x 2 − 2x − 3 = 0 ⇒ a = 1; segundo = −2; c = −3;
re = (−2) 2 − 4 1 (−3) = 16.

D > 0 ⇒ la ecuación tiene dos raíces. Encontrémoslos:

Segunda ecuación:
15 − 2x − x 2 = 0 ⇒ a = −1; segundo = −2; c = 15;
re = (−2) 2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ la ecuación nuevamente tiene dos raíces. vamos a encontrarlos

\[\begin(align) & ((x)_(1))=\frac(2+\sqrt(64))(2\cdot \left(-1 \right))=-5; \\ & ((x)_(2))=\frac(2-\sqrt(64))(2\cdot \left(-1 \right))=3. \\ \end(alinear)\]

Finalmente, la tercera ecuación:
x2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
re = 12 2 − 4 1 36 = 0.

D = 0 ⇒ la ecuación tiene una raíz. Se puede utilizar cualquier fórmula. Por ejemplo, el primero:

Como puedes ver en los ejemplos, todo es muy sencillo. Si conoces las fórmulas y sabes contar, no habrá problemas. La mayoría de las veces, se producen errores al sustituir coeficientes negativos en la fórmula. Una vez más, la técnica descrita anteriormente le ayudará: mire la fórmula literalmente, escriba cada paso y muy pronto se librará de los errores.

Ecuaciones cuadráticas incompletas

Sucede que una ecuación cuadrática es ligeramente diferente de lo que se da en la definición. Por ejemplo:

x2 + 9x = 0;
x 2 - 16 = 0.

Es fácil notar que a estas ecuaciones les falta uno de los términos. Estas ecuaciones cuadráticas son incluso más fáciles de resolver que las estándar: ni siquiera requieren calcular el discriminante. Entonces, introduzcamos un nuevo concepto:

La ecuación ax 2 + bx + c = 0 se llama ecuación cuadrática incompleta si b = 0 o c = 0, es decir el coeficiente de la variable x o del elemento libre es igual a cero.

Por supuesto, es posible un caso muy difícil cuando ambos coeficientes son iguales a cero: b = c = 0. En este caso, la ecuación toma la forma ax 2 = 0. Obviamente, dicha ecuación tiene una única raíz: x = 0.

Consideremos los casos restantes. Sea b = 0, entonces obtenemos una ecuación cuadrática incompleta de la forma ax 2 + c = 0. Transformémosla un poco:

Dado que la raíz cuadrada aritmética sólo existe para un número no negativo, la última igualdad tiene sentido sólo para (−c /a) ≥ 0. Conclusión:

Si en una ecuación cuadrática incompleta de la forma ax 2 + c = 0 se satisface la desigualdad (−c /a) ≥ 0, habrá dos raíces. La fórmula se da arriba;
Si (−c/a)< 0, корней нет.

Como puede ver, no se requería un discriminante: no hay ningún cálculo complejo en ecuaciones cuadráticas incompletas. De hecho, ni siquiera es necesario recordar la desigualdad (−c /a) ≥ 0. Basta expresar el valor x 2 y ver qué hay al otro lado del signo igual. Si hay un número positivo, habrá dos raíces. Si es negativo, no habrá raíces en absoluto.

Ahora veamos ecuaciones de la forma ax 2 + bx = 0, en las que el elemento libre es igual a cero. Aquí todo es sencillo: siempre habrá dos raíces. Basta factorizar el polinomio:

Sacando el factor común de paréntesis

El producto es cero cuando al menos uno de los factores es cero. De aquí vienen las raíces. En conclusión, veamos algunas de estas ecuaciones:

Tarea. Resolver ecuaciones cuadráticas:

x2 − 7x = 0;

5x 2 + 30 = 0;

4x 2 − 9 = 0.

x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.

5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. No hay raíces, porque un cuadrado no puede ser igual a un número negativo.

4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x2 = −1,5.

Maestro : Yurgenson Verónica Alexandrovna

Clase: 9

Artículo: Álgebra

Tema de la lección: Lección de preparación para la OGE en el noveno grado “Ecuaciones cuadráticas”.

Etapa de formación sobre este tema. : preparación para la OGE.

Tipo de lección: Lección de generalización y sistematización del conocimiento.

Objetivo:

Actividad: Formación de las habilidades de los estudiantes para implementar métodos de acción regulatorios.

Contenido: - practicar métodos para resolver ecuaciones cuadráticas;

Desarrollar la capacidad de elegir la solución más racional;

De desarrollo: formar competencias clave de los estudiantes: información (la capacidad de analizar información, comparar, sacar conclusiones), resolución de problemas (la capacidad de plantear problemas y, utilizando el conocimiento existente, encontrar una salida a la situación); comunicativo (capacidad para trabajar en grupos, capacidad para escuchar y oír a los demás, aceptar las opiniones de los demás)

Tareas para el profesor:

Ayudar a actualizar los conocimientos de los estudiantes sobre la resolución de ecuaciones cuadráticas;

Organizar actividades educativas para practicar formas de resolver ecuaciones cuadráticas;

Crear condiciones para la formación de habilidades para desarrollar la capacidad de elegir la solución más racional;

Crear condiciones para la formación de UUD regulatorias: fijación de objetivos, autoestima y autocontrol, planificación.

Tecnología: Entrenamiento multinivel

Métodos de enseñanza: Visual, verbal, método de verificación mutua, método de búsqueda conjunta de una solución óptima, trabajo temporal en grupos, creación de una situación problemática, reproductivo (instrucción, ilustración, explicación, formación práctica). Métodos de autocontrol.

Formas utilizadas para organizar la actividad cognitiva de los estudiantes:

Forma de trabajo colectivo (cuestionamiento frontal, trabajo oral), trabajo en grupo, trabajo individual (trabajo independiente), trabajo por parejas (cuestionamiento mutuo).

Equipos y principales fuentes de información:

Computadora, proyector, pantalla, presentación de la lección sobre el tema "Métodos para resolver ecuaciones cuadráticas".

Ficha de rendimiento para el control y el autocontrol.

Tarjetas-tareas para el trabajo independiente multinivel.

Mapa tecnológico de la lección:

Actividad

alumno

Organizativo

Saludo a los estudiantes

saludo del maestro

Establecer las metas y objetivos de la lección. Motivación para las actividades de aprendizaje de los estudiantes.

En la certificación final, a menudo hay tareas en las que es necesario poder resolver ecuaciones cuadráticas.

Comunicar el propósito de la lección. :

Hoy en la lección repetiremos, generalizaremos e incorporaremos al sistema los tipos, métodos y técnicas estudiados para resolver ecuaciones cuadráticas.

Según los resultados de su trabajo, es decir, según la cantidad de puntos obtenidos, todos recibirán calificaciones.

Lema de la lección: “Pensamos, pensamos, trabajamos y nos ayudamos unos a otros”

(Diapositiva 2 ).

Los profesores están escuchando.

Actualización de conocimientos.

Chicos, normalmente comenzamos la lección revisando nuestra tarea.

¿Quién dirá que era necesario repetir sobre ecuaciones cuadráticas?

¿Qué son las ecuaciones cuadráticas?

¿Qué son?

¿Qué métodos para resolver ecuaciones cuadráticas conoces?

Los profesores responden preguntas y realizan una autoevaluación de sus conocimientos.

Generalización y sistematización del conocimiento.

1. Papel de control mutuo.

Aquí están las ecuaciones. (diapositiva 3)

X 2 + 7 X – 18 = 0;

2 X 2 + 1 = 0;

X 2 –2 X + 9 = 0;

2 y 2 – 3 años + 1 = 0;

2 y 2 = 1;

–2 X 2 – X + 1 = 0;

X 2 + 6 X = 0;

4x 2 =0;

– X 2 – 6 x=1

2 x+x 2 – 1=0

En su mesa hay una tarjeta con preguntas que debe responder (Apéndice 1).

(diapositiva 4 ) Comprobando los resultados, intercambia cartas con tu vecino.

Responder preguntas

2. Trabajo frontal con la clase.

En(diapositiva 5) Se escriben fórmulas a las que les faltan elementos. La tarea de la clase es descubrir qué es esta fórmula y qué falta en la grabación de esta fórmula.

D = b ² – * a * .

D > 0 , significa *raíz.

D * 0 , significa 1 raíz.

D * 0 , Medio * raíces

Responder preguntas

conocimientos correctos.

Resuelve ecuaciones a partir de tarjetas didácticas. Uno de los miembros del grupo mostrará la solución en la pizarra.

Compara tus respuestas con las correctas, por cada respuesta correcta - 1 punto

Resolver ecuaciones

Explica la solución.

Trabajo frontal con la clase.

Dime, ¿podrías responder inmediatamente, sin hacer cálculos, a mi pregunta: "¿Cuál es la suma y el producto de las raíces de una ecuación cuadrática?" (Una persona en la pizarra escribe las fórmulas del teorema de Vieta).

(diapositiva 6)

Siguiente tarea: encuentra verbalmente la suma y la diferencia de las raíces de la ecuación usando el teorema:

(respuestas: 5 y 6; 9 y 20; -3 y 2) Introducción al método de resolución de algunas ecuaciones cuadráticas de forma oral.

El teorema de Vieta se usa ampliamente en ecuaciones de la formaaX 2 + bx + c = 0.

El uso de determinadas propiedades proporciona importantes ventajas para obtener rápidamente respuestas al resolver ecuaciones cuadráticas.

Consideremos estas propiedades.(diapositiva 7)

1) a + b+c = 0 x 1 = 1,x 2 = s/a.

5x 2 + 4x – 9 = 0; X 1 =1,x 2 = - 9/2.

2) un -b+c = 0x 1 = - 1,x 2 = - s/a.

Por ejemplo: 4x 2 + 11x + 7 = 0; X 1 = - 1,x 2 = - 7/4.

(diapositiva 8)

3) un en +c 0

Resuelve la ecuación oralmente: x 2 + bx + ca = 0

Divida sus raíces por a.

a) 2x 2 – 11x + 5 = 0.

Resolvemos la ecuación oralmente: x 2 – 11x + 10 = 0. Sus raíces son 1 y 10. Divide por 2.

Entonces x 1 = ,x 2 = 5.

Respuesta: ; 5.

(diapositiva 9)

c) 6x 2 –7x – 3 = 0

Resolvemos la ecuación oralmente: x 2 –7x – 18 = 0. Sus raíces son -2 y 9. Divide entre 6.

Entonces x 1 = - , x 2 = .

Respuesta: -; .

Responder preguntas. Llenar las lagunas de conocimiento

Trabajar en grupos de varios niveles.

Recepción "Cumplimiento"

Técnica de “captar un error”

Resuelve ecuaciones usando estas propiedades.(diapositiva 10)

Igrupo.

1) encontrar la suma de las raíces de la ecuación

2x 2 – 3x + 1 = 0

2) Encuentra el producto de las raíces de la ecuación.

X 2 +9x +20 = 0

3) resuelve la ecuación

10x 2 – 8x - 2= 0

IIgrupo.

1) encuentra la suma y el producto de las raíces de la ecuación

3x 2 – 8x + 5 = 0

Resolver ecuaciones

2)x 2 + 2x -24 = 0

3)2x 2 -7x +5 = 0

IIIgrupo

Resuelve los problemas:

1)x 2 +5x-6=0

2)5x 2 -7x+2=0

3)100x 2 -99x-199=0

Resolver ecuaciones

Comprueba la solución.

Se lleva a cabo la corrección de conocimientos.

2. Relaciona ecuaciones cuadráticas y métodos para resolverlas:

(diapositiva 11)

2x 2 – 3x + 11 = 0

7x 2 = 8x

X 2 – 10x + 100 = 0

X 2 –5x –6 = 0

– 2x 2 + x +14= 0

-factorización

- fórmula general de raíces

-Teorema de Vieta

3. Encuentra errores al resolver ecuaciones =

Los chicos que completan el trabajo rápidamente pueden resolver una tarea adicional.(diapositiva 14), escrito en la pizarra.

Después de la ejecución, se realiza una comprobación rápida.(diapositiva 15)

Ahora cuenta el número total de puntos y ponte una calificación.(diapositiva 16)

30-24 puntos – puntuación 5;

23-18 puntos – puntuación 4;

12-17 puntos –. puntuación4

Y el maestro califica a todos por su actividad, coraje y perseverancia. Bueno, si hoy alguien no logró sumar puntos por una evaluación positiva, entonces el éxito todavía está por delante y definitivamente estará con usted la próxima vez.

Resolver ecuaciones

realizar una autoevaluación.

Reflexión.

¿Quién puede decir lo que repetimos hoy en clase?

¿Te gustó cómo lo hicimos?

Continúa las frases:

Ahora lo sé con seguridad...

Entiendo …

He aprendido …

Mi opinión …

Todos tienen cartas de colores sobre la mesa.

Si está contento y satisfecho con la lección, presente una tarjeta verde.

Si la lección es interesante y trabajaste activamente, recibirás una tarjeta amarilla.

realizar una autoevaluación.

Tarea

(diapositiva 17) Resolver ecuaciones de la colección de tareas.

Certificación final estatal

Graduados de noveno grado.

AV. Semenov, A. S. Trepalin, I. V. Yashchenko

por nivel

Selecciona tareas según tu nivel

Análisis de la tarea nº 4 sobre el tema: "Resolver ecuaciones de varios tipos"

Materiales adicionales
Estimados usuarios, ¡no olviden dejar sus comentarios, reseñas, deseos! Todos los materiales han sido revisados por un programa antivirus.

Ayudas educativas y simuladores en la tienda online de Integral para 9º grado
Manual interactivo "Reglas y ejercicios de álgebra" para noveno grado.
Libro de texto multimedia para noveno grado "Álgebra en 10 minutos"

La tarea número 4 requiere la capacidad de resolver ecuaciones de varios tipos. Chicos, deberían conocer bien los métodos para resolver correctamente ecuaciones cuadráticas, ecuaciones racionales fraccionarias y ecuaciones lineales ordinarias. También deberías ser bueno realizando operaciones con polinomios: multiplicar y dividir un polinomio por un polinomio. ¿Necesita la capacidad de seleccionar las raíces de una ecuación que están incluidas en el área de solución y determinar qué raíces deben descartarse y no tomarse en cuenta?

Lecciones que le ayudarán a preparar esta tarea:

1.Definiciones básicas y ejemplos de soluciones de funciones lineales.
2. Concepto y forma estándar de monomio.
3. Polinomio, forma estándar, reducción, transformación.
4. Ejemplos de expresiones numéricas. Expresiones algebraicas con variables y operaciones con ellas.
5. Ecuaciones, ejemplos de resolución de ecuaciones.
6. Ecuaciones cuadráticas. Lección en progreso.
7. Ecuaciones racionales fraccionarias. Lección en progreso.
8. Raíz cuadrada. Lección en progreso.

Pasemos al análisis de ejemplos de soluciones.

Ejemplo 1.
Encuentra las raíces de la ecuación: $16x^2-1=0$.

Solución.
Tenga en cuenta que se nos da una ecuación cuadrática, pero no completa. El coeficiente de x es cero. Luego nos guiaremos por la regla: "dejaremos aquellas expresiones en las que hay x al cuadrado a la izquierda y moveremos todos los números a la derecha".
Transformemos nuestra expresión: $16x^2=1$.

Dividamos ambos lados de la ecuación por el coeficiente de x al cuadrado: $x^2=\frac(1)(16)$.

Para resolver esta ecuación, necesitamos conocer la raíz cuadrada. Extraigamos la raíz, sin olvidar que también debemos tener en cuenta el número negativo: $x=±\sqrt(\frac(1)(16))=±\frac(1)(4)=±0.25$.
Respuesta: $x=±0,25$.

Ejemplo 2.
Resuelve la ecuación: $x^2=18-7x$.

Solución.
Movamos todas las expresiones al lado izquierdo de la ecuación: $x^2+7x-18=0$.

Podemos resolver la ecuación cuadrática habitual de dos formas:
1. “de frente”, calculando el discriminante;
2. usando el teorema de Viette.

1 vía.
Anotemos todos los coeficientes de la ecuación cuadrática: $a=1$, $b=7$, $c=-18$.

Encontremos el discriminante: $D=b^2-4ac=(7)^2-4*1*(-18)=49+72=121=(11)^2>0$.
Encontramos que la ecuación tiene 2 raíces.
Sólo tenemos que encontrar estas raíces:
$x_1=\frac(-b+\sqrt(D))(2a)=\frac(-7+11)(2)=2$.
$x_2=\frac(-b-\sqrt(D))(2a)=\frac(-7-11)(2)=-9$.

Método 2.
Usemos el teorema de Viette. El teorema de Viette a menudo simplifica muchas veces la solución de ecuaciones cuadráticas, especialmente cuando el coeficiente $a=1$. En este caso, el producto de las raíces de la ecuación es igual al coeficiente $c$, y la suma de las raíces de la ecuación es igual a menos el coeficiente de $b$:
$x_1+x_2=-\frac(b)(a)$.
$x_1*x_2=\frac(c)(a)$.

En nuestro ejemplo, $с=-18$ y $b=7$. Empezamos a clasificar pares de números cuyo producto es igual a menos dieciocho. Los primeros números que me vienen a la mente son nueve y dos. Después de realizar algunas multiplicaciones y sumas simples, podemos verificar que las raíces $x=-9$ y $x=2$ son adecuadas para nosotros.
$x_1*x_2=-9*2=-18=\frac(c)(a)$.
x$_1+x_2=-9+2=-7=-\frac(b)(a)$.
Respuesta: $x=-9$, $x=2$.

Ejemplo 3.
Resuelve la ecuación: $x-\frac(x)(7)=\frac(15)(7)$.

Solución.
Se nos da una ecuación lineal ordinaria con coeficientes fraccionarios. Para resolver esta ecuación necesitas trabajar correctamente con fracciones ordinarias.
El primer paso es transformar el lado izquierdo de la ecuación, simplificándola: $x-\frac(x)(7)=\frac(7x)(7)-\frac(x)(7)=\frac(6x )(7)$.
Obtuvimos la ecuación: $\frac(6x)(7)=\frac(15)(7)$.
Dividamos el lado derecho de la ecuación por el coeficiente de x: $x=\frac(\frac(15)(7))(\frac(6)(7))$.

Consideremos la división por separado: $\frac(\frac(15)(7))(\frac(6)(7))=\frac(15)(7)*\frac(7)(6)=\frac( 15 )(6)=2\frac(3)(6)=2\frac(1)(2)=$2.5.

Recibimos: $x=2.5$.
Respuesta: $x=2,5$.

Ejemplo 4.
Resuelve la ecuación: $(x+2)^2=(x-4)^2$.

Solución.
Método 1.
Usemos la fórmula para el cuadrado de la suma: $(x+2)^2=x^2+4x+4$.
$(x-4)^2=x^2-8x+16$.
Recibimos: $x^2+4x+4=x^2-8x+16$.
Simplifiquemos nuestra ecuación:
$x^2+4x-x^2+8x=16-4$.
$12x=$12.
$x=1$.

Método 2.
Para resolver esta ecuación, podemos usar la fórmula de diferencia de cuadrados. $(x+2)^2-(x-4)^2=0$.
$(x+2+x-4)(x+2-x+4)=0$.
$(2x-2)*(6)=0$.
$2x-2=0$.
$2x=2$.
$x=1$.
Respuesta: $x=1$.

Ejemplo 5.
Resuelve la ecuación: $\frac(9)(x-14)=\frac(14)(x-9)$.

Solución.
Se nos presenta una ecuación racional fraccionaria. Al resolver estas ecuaciones, vale la pena recordar que no se puede dividir por cero. Por lo tanto, las raíces de la ecuación siempre deben verificarse sustituyéndolas en el denominador de la ecuación original.
Usemos la regla de multiplicación cruz por cruz: $9(x-9)=14(x-14)$.
Tenemos una ecuación lineal:
$9x-81=14x-196$.
$9x-14x=-196+81$.
$-5x=-115$.
$x=23$.
Habiendo comprobado nuestra raíz, nos aseguramos de que los denominadores de las fracciones de la ecuación original no desaparezcan.
Respuesta: $x=23$.

Ejemplo 6.
Encuentre soluciones que satisfagan el sistema: $\begin (cases) x^2+9x-22=0, \\ x≤1 \end (cases)$.

Solución.
Primero, resolvamos la ecuación cuadrática usando el teorema de Viette. El producto de nuestras raíces es $22$ y la suma es $-9$.
Seleccionemos las raíces:
$-11*2=-22$.
$-11+2=-9$.
Tenemos dos raíces: $x_1=-11$ y $x_2=2$. De estas raíces, la desigualdad $x≤1$ la satisface la primera raíz, y esa será la respuesta.
Respuesta: $x=-11$.

Ejemplo 7.
Resuelve la ecuación: $23x-60-x^2=0$.
En tu respuesta, indica el módulo de diferencia de las raíces.

Solución.
Multipliquemos la ecuación original por $-1$: $x^2-23x+60=0$.
De esta forma, la ecuación parece mucho más familiar.
Usemos el teorema de Viette y presentemos nuestra ecuación como producto de binomios:
$(x-20)(x-3)=0$.
Tenemos dos raíces $x_1=20$ y $x_2=3$.
Encontremos el módulo de diferencia: $|x_1-x_2|=|20-3|=|17|=17$.
Respuesta: 17.

Ejemplo 8.
¿Cuántas raíces tiene la ecuación $x^6-x^2=0?$

Solución.
Saquemos el grado más pequeño entre paréntesis: $x^2(x^4-1)=0$.
Ahora usemos la fórmula de diferencia de cuadrados:
$x^2 (x^2-1)(x^2+1)=0$.
Y usemos la misma fórmula nuevamente:
$x^2 (x-1)(x+1)(x^2+1)=0$.
Esta ecuación es equivalente a un conjunto de ecuaciones: encontramos que esta ecuación tiene tres raíces.
Respuesta: 3.

Ejemplo 9.
Resuelve la ecuación: $\frac((x-2)(2x+1))(2-x)=0$.
Si la ecuación tiene más de una raíz, escribe la más grande como respuesta.

Solución.
La ecuación original es equivalente al siguiente conjunto: Resolvamos cada ecuación: Como el denominador de la fracción no puede ser igual a cero, se elimina una solución. Obtuvimos una raíz de la ecuación $x=-0.5$.
Respuesta: -0,5.

Alejandro Shabalin

! De la teoría a la práctica;

! De lo simple a lo complejo

MAOU "Escuela secundaria Platoshin",

profesora de matemáticas, Melekhina G.V.

Forma general de una ecuación lineal: hacha + b = 0 ,

Dónde a Y b– números (coeficientes).

Si un = 0 Y segundo = 0, Eso 0x + 0 = 0 – infinitas raíces;
Si un = 0 Y segundo ≠ 0, Eso 0x + segundo = 0– ninguna solución;
Si un ≠ 0 Y b = 0 , Eso hacha + 0 = 0 – una raíz, x = 0;
Si un ≠ 0 Y b ≠ 0 , Eso hacha + b = 0 – una raíz,

! Si X está elevado a la primera potencia y no está en el denominador, entonces es una ecuación lineal.

! Y si la ecuación lineal es complejo :

! Los términos con X van hacia la izquierda, sin X, hacia la derecha.

! Estas ecuaciones son también lineal .

! La principal propiedad de la proporción (transversal).

! Abre los corchetes, con X a la izquierda, sin X a la derecha.

si el coeficiente un = 1, entonces la ecuación se llama dado :

si el coeficiente b = 0 o y c = 0, entonces la ecuación se llama incompleto :

! Fórmulas básicas

! Más fórmulas

Ecuación bicuadrática- llamada ecuación de la forma hacha 4 +bx 2 + c = 0 .

La ecuación bicuadrática se reduce a ecuación cuadrática usando sustitución, entonces

Obtenemos una ecuación cuadrática:

Busquemos las raíces y volvamos al reemplazo:

Ejemplo 1:

Resolver ecuación x 4 + 5x 2 – 36 = 0.

Solución:

Sustitución: x 2 = t.

t 2 + 5t – 36 = 0. Las raíces de la ecuación son t 1 = -9 y t 2 = 4.

x2 = -9 o x2 = 4.

Respuesta: No hay raíces en la primera ecuación, pero sí en la segunda: x = ±2.

Ejemplo 2:

Resuelve la ecuación (2х – 1) 4 – 25(2x – 1) 2 + 144 = 0.

Solución:

Sustitución: (2x – 1) 2 = t.

t 2 – 25t + 144 = 0. Las raíces de la ecuación son t 1 = 9 y t 2 = 16.

(2x – 1) 2 = 9 o (2x – 1) 2 = 16.

2x – 1 = ±3 o 2x – 1 = ±4.

La primera ecuación tiene dos raíces: x = 2 y x = -1, la segunda también tiene dos raíces: x = 2,5 y x = -1,5.

Respuesta: -1,5; -1; 2; 2.5.

1) X 4 - 9 X 2 = 0; 2) 4 X 4 -x2 = 0;

1) X 4 +x 2 - 2 = 0;

2) X 4 - 3 X 2 - 4 = 0; 3) 9 X 4 + 8 X 2 - 1 = 0; 4) 20 X 4 - X 2 - 1 = 0.

Resuelve ecuaciones seleccionando desde el lado izquierdo cuadrado lleno :

1) X 4 - 20 X 2 + 64 = 0; 2) X 4 - 13 X 2 + 36 = 0; 3) X 4 - 4 X 2 + 1 = 0; 4) X 4 + 2 X 2 +1 = 0.

! Recuerda el cuadrado de la suma y el cuadrado de la diferencia.

Expresión racional es una expresión algebraica formada por números y una variable X utilizando las operaciones de suma, resta, multiplicación, división y exponenciación con exponente natural.

Si r(x) es una expresión racional, entonces la ecuación r(x)=0 llama ecuación racional.

Algoritmo para resolver una ecuación racional:

1. Mueve todos los términos de la ecuación a un lado.

2. Convierte esta parte de la ecuación a una fracción algebraica. p(x)/q(x)

3. Resuelve la ecuación p(x)=0

4. Para cada raíz de la ecuación p(x)=0 comprobar si cumple la condición q(x)≠0 O no. En caso afirmativo, entonces esta es la raíz de la ecuación dada; si no, entonces es una raíz extraña y no debe incluirse en la respuesta.

! Recordemos la solución de la ecuación racional fraccionaria:

! Para resolver ecuaciones, es útil recordar las fórmulas de multiplicación abreviadas:

Si una ecuación contiene una variable bajo el signo de la raíz cuadrada, entonces la ecuación se llama irracional .

Método de elevar al cuadrado ambos lados de una ecuación.- el método principal para resolver ecuaciones irracionales.

Una vez resuelta la ecuación racional resultante, es necesario controlar , eliminando posibles raíces extrañas.

Respuesta: 5; 4

Otro ejemplo:

Examen:

La expresión no tiene significado.

Respuesta: sin soluciones.

En el término "ecuación cuadrática", la palabra clave es "cuadrática". Esto significa que la ecuación debe contener necesariamente una variable (esa misma x) al cuadrado, y no debe haber xes a la tercera (o mayor) potencia.

La solución de muchas ecuaciones se reduce a resolver ecuaciones cuadráticas.

Aprendamos a determinar que se trata de una ecuación cuadrática y no de otra ecuación.

Ejemplo 1.

Eliminemos el denominador y multipliquemos cada término de la ecuación por

Movamos todo hacia el lado izquierdo y ordenemos los términos en orden descendente de potencias de X.

¡Ahora podemos decir con confianza que esta ecuación es cuadrática!

Ejemplo 2.

Multiplica los lados izquierdo y derecho por:

¡Esta ecuación, aunque estaba originalmente en ella, no es cuadrática!

Ejemplo 3.

Multipliquemos todo por:

¿Aterrador? El cuarto y segundo grado... Sin embargo, si hacemos una sustitución, veremos que tenemos una ecuación cuadrática simple:

Ejemplo 4.

Parece estar ahí, pero echemos un vistazo más de cerca. Movamos todo hacia el lado izquierdo:

Mira, se ha reducido y ¡ahora es una ecuación lineal simple!

Ahora intenta determinar por ti mismo cuáles de las siguientes ecuaciones son cuadráticas y cuáles no:

Ejemplos:

Respuestas:

cuadrado;
cuadrado;
no cuadrado;
no cuadrado;
no cuadrado;
cuadrado;
no cuadrado;
cuadrado.

Los matemáticos convencionalmente dividen todas las ecuaciones cuadráticas en los siguientes tipos:

Completar ecuaciones cuadráticas- ecuaciones en las que los coeficientes y, así como el término libre c, no son iguales a cero (como en el ejemplo). Además, entre las ecuaciones cuadráticas completas hay dado- estas son ecuaciones en las que el coeficiente (la ecuación del ejemplo uno no solo es completa, ¡sino también reducida!)

Ecuaciones cuadráticas incompletas- ecuaciones en las que el coeficiente yo el término libre c son iguales a cero:
Están incompletos porque les falta algún elemento. ¡¡¡Pero la ecuación siempre debe contener x al cuadrado!!! De lo contrario, ya no será una ecuación cuadrática, sino alguna otra ecuación.

¿Por qué se les ocurrió tal división? Parecería que hay una X al cuadrado, y está bien. Esta división está determinada por los métodos de solución. Veamos cada uno de ellos con más detalle.

Resolver ecuaciones cuadráticas incompletas

Primero, centrémonos en resolver ecuaciones cuadráticas incompletas: ¡son mucho más simples!

Hay tipos de ecuaciones cuadráticas incompletas:

, en esta ecuación el coeficiente es igual.
, en esta ecuación el término libre es igual a.
, en esta ecuación el coeficiente y el término libre son iguales.

1. yo. Como sabemos sacar la raíz cuadrada, expresemos a partir de esta ecuación

La expresión puede ser negativa o positiva. Un número al cuadrado no puede ser negativo, porque al multiplicar dos números negativos o dos positivos, el resultado siempre será un número positivo, entonces: si, entonces la ecuación no tiene soluciones.

Y si, entonces obtenemos dos raíces. No es necesario memorizar estas fórmulas. Lo principal es que debes saber y recordar siempre que no puede ser menos.

Intentemos resolver algunos ejemplos.

Ejemplo 5:

Resuelve la ecuación

Ahora solo queda extraer la raíz de los lados izquierdo y derecho. Después de todo, ¿recuerdas cómo extraer las raíces?

Respuesta:

¡¡¡Nunca te olvides de las raíces con signo negativo!!!

Ejemplo 6:

Resuelve la ecuación

Respuesta:

Ejemplo 7:

Resuelve la ecuación

¡Oh! El cuadrado de un número no puede ser negativo, lo que significa que la ecuación

¡sin raíces!

Para este tipo de ecuaciones que no tienen raíces, los matemáticos crearon un icono especial: (conjunto vacío). Y la respuesta se puede escribir así:

Respuesta:

Por tanto, esta ecuación cuadrática tiene dos raíces. Aquí no hay restricciones, ya que no extrajimos la raíz.
Ejemplo 8:

Resuelve la ecuación

Saquemos el factor común de paréntesis:

De este modo,

Esta ecuación tiene dos raíces.

Respuesta:

El tipo más simple de ecuaciones cuadráticas incompletas (aunque todas son simples, ¿verdad?). Obviamente, esta ecuación siempre tiene una sola raíz:

Aquí prescindiremos de ejemplos.

Resolver ecuaciones cuadráticas completas

Te recordamos que una ecuación cuadrática completa es una ecuación de la forma ecuación donde

Resolver ecuaciones cuadráticas completas es un poco más difícil (sólo un poco) que éstas.

Recordar, ¡Cualquier ecuación cuadrática se puede resolver usando un discriminante! Incluso incompleto.

Los otros métodos te ayudarán a hacerlo más rápido, pero si tienes problemas con ecuaciones cuadráticas, primero domina la solución usando el discriminante.

1. Resolver ecuaciones cuadráticas usando un discriminante.

Resolver ecuaciones cuadráticas con este método es muy sencillo, lo principal es recordar la secuencia de acciones y un par de fórmulas.

Si, entonces la ecuación tiene raíz, debes prestar especial atención al paso. Discriminante () nos dice el número de raíces de la ecuación.

Si, entonces la fórmula del paso se reducirá a. Por tanto, la ecuación sólo tendrá raíz.
Si es así, no podremos extraer la raíz del discriminante en el paso. Esto indica que la ecuación no tiene raíces.

Volvamos a nuestras ecuaciones y veamos algunos ejemplos.

Ejemplo 9:

Resuelve la ecuación

Paso 1 saltamos.

Paso 2.

Hallamos el discriminante:

Esto significa que la ecuación tiene dos raíces.

Paso 3.

Respuesta:

Ejemplo 10:

Resuelve la ecuación

La ecuación se presenta en forma estándar, por lo que Paso 1 saltamos.

Paso 2.

Hallamos el discriminante:

Esto significa que la ecuación tiene una raíz.

Respuesta:

Ejemplo 11:

Resuelve la ecuación

La ecuación se presenta en forma estándar, por lo que Paso 1 saltamos.

Paso 2.

Hallamos el discriminante:

Esto significa que no podremos extraer la raíz del discriminante. No hay raíces de la ecuación.

Ahora sabemos cómo escribir correctamente esas respuestas.

Respuesta: sin raíces

2. Resolver ecuaciones cuadráticas usando el teorema de Vieta.

Si recuerdas, existe un tipo de ecuación que se llama reducida (cuando el coeficiente a es igual a):

Estas ecuaciones son muy fáciles de resolver utilizando el teorema de Vieta:

suma de raices dado la ecuación cuadrática es igual y el producto de las raíces es igual.

Ejemplo 12:

Resuelve la ecuación

Esta ecuación se puede resolver usando el teorema de Vieta porque .

La suma de las raíces de la ecuación es igual, es decir. obtenemos la primera ecuación:

Y el producto es igual a:

Compongamos y resolvamos el sistema:

Y. La cantidad es igual a;
Y. La cantidad es igual a;
Y. La cantidad es igual.

y son la solución al sistema:

Respuesta: ; .

Ejemplo 13:

Resuelve la ecuación

Respuesta:

Ejemplo 14:

Resuelve la ecuación

Se da la ecuación, lo que significa:

Respuesta:

ECUACIONES CUADRÁTICAS. NIVEL PROMEDIO

¿Qué es una ecuación cuadrática?

En otras palabras, una ecuación cuadrática es una ecuación de la forma donde - la incógnita, - algunos números y.

El número se llama el más alto o primer coeficiente ecuación cuadrática, - segundo coeficiente, A - miembro gratuito.

¿Por qué? Porque si la ecuación se vuelve inmediatamente lineal, porque desaparecerá.

En este caso, y puede ser igual a cero. En esta silla la ecuación se llama incompleta. Si todos los términos están en su lugar, es decir, la ecuación está completa.

Soluciones a varios tipos de ecuaciones cuadráticas.

Métodos para resolver ecuaciones cuadráticas incompletas:

Primero, veamos los métodos para resolver ecuaciones cuadráticas incompletas: son más simples.

Podemos distinguir los siguientes tipos de ecuaciones:

I., en esta ecuación el coeficiente y el término libre son iguales.

II. , en esta ecuación el coeficiente es igual.

III. , en esta ecuación el término libre es igual a.

Ahora veamos la solución para cada uno de estos subtipos.

Obviamente, esta ecuación siempre tiene una sola raíz:

Un número al cuadrado no puede ser negativo, porque al multiplicar dos números negativos o dos positivos, el resultado siempre será un número positivo. Es por eso:

si, entonces la ecuación no tiene soluciones;

si tenemos dos raíces

No es necesario memorizar estas fórmulas. Lo principal a recordar es que no puede ser menos.

Ejemplos:

Soluciones:

Respuesta:

¡Nunca te olvides de las raíces con signo negativo!

El cuadrado de un número no puede ser negativo, lo que significa que la ecuación

sin raíces.

Para anotar brevemente que un problema no tiene solución utilizamos el icono de conjunto vacío.

Respuesta:

Entonces, esta ecuación tiene dos raíces: y.

Respuesta:

Saquemos el factor común de paréntesis:

El producto es igual a cero si al menos uno de los factores es igual a cero. Esto significa que la ecuación tiene solución cuando:

Entonces, esta ecuación cuadrática tiene dos raíces: y.

Ejemplo:

Resuelve la ecuación.

Solución:

Factoricemos el lado izquierdo de la ecuación y encontremos las raíces:

Respuesta:

Métodos para resolver ecuaciones cuadráticas completas:

1. Discriminante

Resolver ecuaciones cuadráticas de esta forma es fácil, lo principal es recordar la secuencia de acciones y un par de fórmulas. Recuerde, ¡cualquier ecuación cuadrática se puede resolver usando un discriminante! Incluso incompleto.

¿Notaste la raíz del discriminante en la fórmula de raíces? Pero el discriminante puede ser negativo. ¿Qué hacer? Necesitamos prestar especial atención al paso 2. El discriminante nos dice el número de raíces de la ecuación.

Si, entonces la ecuación tiene raíces:
Si, entonces la ecuación tiene las mismas raíces y, de hecho, una raíz:
Estas raíces se llaman raíces dobles.
Si, entonces no se extrae la raíz del discriminante. Esto indica que la ecuación no tiene raíces.

¿Por qué son posibles diferentes números de raíces? Pasemos al significado geométrico de la ecuación cuadrática. La gráfica de la función es una parábola:

En un caso especial, que es una ecuación cuadrática, . Esto significa que las raíces de una ecuación cuadrática son los puntos de intersección con el eje de abscisas (eje). Una parábola puede no cruzar el eje en absoluto, o puede cruzarlo en uno (cuando el vértice de la parábola se encuentra en el eje) o dos puntos.

Además, el coeficiente es responsable de la dirección de las ramas de la parábola. Si, entonces las ramas de la parábola se dirigen hacia arriba, y si, hacia abajo.

Ejemplos:

Soluciones:

Respuesta:

Respuesta: .

Respuesta:

Esto significa que no hay soluciones.

Respuesta: .

2. Teorema de Vieta

Es muy fácil utilizar el teorema de Vieta: basta con elegir un par de números cuyo producto sea igual al término libre de la ecuación, y la suma sea igual al segundo coeficiente tomado con el signo opuesto.

Es importante recordar que el teorema de Vieta sólo se puede aplicar en ecuaciones cuadráticas reducidas ().

Veamos algunos ejemplos:

Ejemplo 1:

Resuelve la ecuación.

Solución:

Esta ecuación se puede resolver usando el teorema de Vieta porque . Otros coeficientes: ; .

La suma de las raíces de la ecuación es:

Y el producto es igual a:

Seleccionemos pares de números cuyo producto sea igual y comprobemos si su suma es igual:

Y. La cantidad es igual a;
Y. La cantidad es igual a;
Y. La cantidad es igual.

y son la solución al sistema:

Por tanto, y son las raíces de nuestra ecuación.

Respuesta: ; .

Ejemplo #2:

Solución:

Seleccionemos pares de números que dan el producto y luego verifiquemos si su suma es igual:

y: dan en total.

y: dan en total. Para obtenerlo, basta con cambiar los signos de las supuestas raíces: y, al fin y al cabo, el producto.

Respuesta:

Ejemplo #3:

Solución:

El término libre de la ecuación es negativo y, por tanto, el producto de las raíces es un número negativo. Esto sólo es posible si una de las raíces es negativa y la otra es positiva. Por lo tanto la suma de las raíces es igual a diferencias de sus módulos.

Seleccionemos pares de números que dan en el producto, y cuya diferencia es igual a:

y: su diferencia es igual - no encaja;

y: - no apto;

y: - adecuado. Sólo queda recordar que una de las raíces es negativa. Como su suma debe ser igual, la raíz con el módulo menor debe ser negativa: . Verificamos:

Respuesta:

Ejemplo #4:

Resuelve la ecuación.

Solución:

Se da la ecuación, lo que significa:

El término libre es negativo y, por tanto, el producto de las raíces es negativo. Y esto sólo es posible cuando una raíz de la ecuación es negativa y la otra es positiva.

Seleccionemos pares de números cuyo producto sea igual y luego determinemos qué raíces deben tener un signo negativo:

Evidentemente, sólo las raíces y son aptas para la primera condición:

Respuesta:

Ejemplo #5:

Resuelve la ecuación.

Solución:

Se da la ecuación, lo que significa:

La suma de las raíces es negativa, lo que significa que al menos una de las raíces es negativa. Pero como su producto es positivo, significa que ambas raíces tienen un signo menos.

Seleccionemos pares de números cuyo producto sea igual a:

Obviamente, las raíces son los números y.

Respuesta:

De acuerdo, es muy conveniente encontrar raíces oralmente, en lugar de contar este desagradable discriminante. Intente utilizar el teorema de Vieta con la mayor frecuencia posible.

Pero el teorema de Vieta es necesario para facilitar y acelerar la búsqueda de las raíces. Para que puedas beneficiarte de su uso, debes llevar las acciones al automatismo. Y para ello, resuelve cinco ejemplos más. Pero no hagas trampa: ¡no puedes utilizar un discriminante! Sólo el teorema de Vieta:

Soluciones a tareas para el trabajo independiente:

Tarea 1. ((x)^(2))-8x+12=0

Según el teorema de Vieta:

Como es habitual, comenzamos la selección con la pieza:

No apto por la cantidad;

: la cantidad es justo lo que necesitas.

Respuesta: ; .

Tarea 2.

Y nuevamente nuestro teorema favorito de Vieta: la suma debe ser igual y el producto debe ser igual.

Pero como no debe ser, pero, cambiamos los signos de las raíces: y (en total).

Respuesta: ; .

Tarea 3.

Mmmm... ¿Dónde es eso?

Debes mover todos los términos en una sola parte:

La suma de las raíces es igual al producto.

¡Está bien, detente! La ecuación no está dada. Pero el teorema de Vieta sólo es aplicable en las ecuaciones dadas. Entonces primero necesitas dar una ecuación. Si no puedes liderar, abandona esta idea y resuélvela de otra manera (por ejemplo, a través de un discriminante). Permítanme recordarles que dar una ecuación cuadrática significa igualar el coeficiente principal:

Excelente. Entonces la suma de las raíces es igual a y el producto.

Aquí elegir es muy fácil: después de todo, es un número primo (perdón por la tautología).

Respuesta: ; .

Tarea 4.

El miembro gratuito es negativo. ¿Qué tiene de especial esto? Y es que las raíces tendrán signos diferentes. Y ahora, durante la selección, comprobamos no la suma de las raíces, sino la diferencia en sus módulos: esta diferencia es igual, pero es un producto.

Entonces, las raíces son iguales a y, pero una de ellas es menos. El teorema de Vieta nos dice que la suma de las raíces es igual al segundo coeficiente con signo opuesto, es decir. Esto significa que la raíz más pequeña tendrá un signo menos: y desde entonces.

Respuesta: ; .

Tarea 5.

¿Qué deberías hacer primero? Así es, da la ecuación:

Nuevamente: seleccionamos los factores del número y su diferencia debe ser igual a:

Las raíces son iguales a y, pero una de ellas es menos. ¿Cual? Su suma debe ser igual, lo que significa que el menos tendrá una raíz mayor.

Respuesta: ; .

Déjame resumir:

El teorema de Vieta se utiliza sólo en las ecuaciones cuadráticas dadas.
Usando el teorema de Vieta, puedes encontrar las raíces por selección, de forma oral.
Si no se da la ecuación o no se encuentra un par adecuado de factores del término libre, entonces no hay raíces enteras y es necesario resolverla de otra manera (por ejemplo, mediante un discriminante).

3. Método para seleccionar un cuadrado completo

Si todos los términos que contienen la incógnita se representan en forma de términos de fórmulas de multiplicación abreviadas (el cuadrado de la suma o la diferencia), luego de reemplazar las variables, la ecuación se puede presentar en forma de una ecuación cuadrática incompleta del tipo.

Por ejemplo:

Ejemplo 1:

Resuelve la ecuación: .

Solución:

Respuesta:

Ejemplo 2:

Resuelve la ecuación: .

Solución:

Respuesta:

En general, la transformación se verá así:

Esto implica: .

¿No te recuerda a nada? ¡Esto es algo discriminatorio! Así es exactamente como obtuvimos la fórmula discriminante.

ECUACIONES CUADRÁTICAS. BREVEMENTE SOBRE LAS COSAS PRINCIPALES

Ecuación cuadrática- esta es una ecuación de la forma donde - la incógnita, - los coeficientes de la ecuación cuadrática, - el término libre.

Ecuación cuadrática completa- una ecuación en la que los coeficientes no son iguales a cero.

Ecuación cuadrática reducida- una ecuación en la que el coeficiente, es decir: .

Ecuación cuadrática incompleta- una ecuación en la que el coeficiente yo el término libre c son iguales a cero:

si el coeficiente, la ecuación se ve así: ,
si hay un término libre, la ecuación tiene la forma: ,
si y, la ecuación se ve así: .

1. Algoritmo para resolver ecuaciones cuadráticas incompletas.

1.1. Una ecuación cuadrática incompleta de la forma, donde:

1) Expresemos la incógnita: ,

2) Verifique el signo de la expresión:

si, entonces la ecuación no tiene soluciones,
si, entonces la ecuación tiene dos raíces.

1.2. Una ecuación cuadrática incompleta de la forma, donde:

1) Saquemos el factor común de paréntesis: ,

2) El producto es igual a cero si al menos uno de los factores es igual a cero. Por tanto, la ecuación tiene dos raíces:

1.3. Una ecuación cuadrática incompleta de la forma, donde:

Esta ecuación siempre tiene una sola raíz: .

2. Algoritmo para resolver ecuaciones cuadráticas completas de la forma donde

2.1. Solución usando discriminante

1) Llevemos la ecuación a la forma estándar: ,

2) Calculemos el discriminante usando la fórmula: , que indica el número de raíces de la ecuación:

3) Encuentra las raíces de la ecuación:

si, entonces la ecuación tiene raíces, que se encuentran mediante la fórmula:
si, entonces la ecuación tiene una raíz, que se encuentra mediante la fórmula:
si, entonces la ecuación no tiene raíces.

2.2. Solución usando el teorema de Vieta

La suma de las raíces de la ecuación cuadrática reducida (ecuación de la forma donde) es igual y el producto de las raíces es igual, es decir , A.

2.3. Solución por el método de selección de un cuadrado completo.

Si una ecuación cuadrática de la forma tiene raíces, entonces se puede escribir en la forma: .

Bueno, se acabó el tema. Si estás leyendo estas líneas es que eres muy guay.

Porque sólo el 5% de las personas son capaces de dominar algo por sí mismas. Y si lees hasta el final, ¡estás en este 5%!

Ahora lo más importante.

Has entendido la teoría sobre este tema. Y, repito, esto... ¡esto es simplemente genial! Ya eres mejor que la gran mayoría de tus compañeros.

El problema es que esto puede no ser suficiente...

¿Para qué?

Por aprobar con éxito el Examen Estatal Unificado, por ingresar a la universidad con un presupuesto limitado y, LO MÁS IMPORTANTE, de por vida.

No te convenceré de nada, solo diré una cosa...

Las personas que han recibido una buena educación ganan mucho más que quienes no la han recibido. Esto es estadística.

Pero esto no es lo principal.

Lo principal es que son MÁS FELICES (existen estudios de este tipo). ¿Quizás porque se abren ante ellos muchas más oportunidades y la vida se vuelve más brillante? No lo sé...

Pero piensa por ti mismo...

¿Qué se necesita para estar seguro de ser mejor que otros en el Examen Estatal Unificado y, en última instancia, ser... más feliz?

GANA TU MANO RESOLVIENDO PROBLEMAS SOBRE ESTE TEMA.

No te pedirán teoría durante el examen.

Necesitará resolver problemas contra el tiempo.

Y, si no los has resuelto (¡MUCHO!), seguro que cometerás un error estúpido en alguna parte o simplemente no tendrás tiempo.

Es como en los deportes: hay que repetirlo muchas veces para ganar con seguridad.

Encuentra la colección donde quieras, necesariamente con soluciones, análisis detallado.¡Y decide, decide, decide!

Puedes utilizar nuestras tareas (opcional) y nosotros, por supuesto, te las recomendamos.

Para mejorar el uso de nuestras tareas, debe ayudar a extender la vida útil del libro de texto YouClever que está leyendo actualmente.

¿Cómo? Hay dos opciones:

Desbloquee todas las tareas ocultas en este artículo:
Desbloquee el acceso a todas las tareas ocultas en los 99 artículos del libro de texto. Comprar un libro de texto - 899 RUR

Sí, tenemos 99 artículos de este tipo en nuestro libro de texto y el acceso a todas las tareas y a todos los textos ocultos que contienen se puede abrir inmediatamente.

El acceso a todas las tareas ocultas se proporciona durante TODA la vida útil del sitio.

En conclusión...

Si no te gustan nuestras tareas, busca otras. Simplemente no te quedes en la teoría.

“Entendido” y “Puedo resolver” son habilidades completamente diferentes. Necesitas ambos.

¡Encuentra problemas y resuélvelos!