The formula for the area of ​​a curvilinear trapezoid. Definite integral. How to calculate the area of ​​a figure. Finding the area of ​​a curved sector

Definition. The figure bounded by the graph of a continuous, sign-constant function f(x), the abscissa axis and the straight lines x=a, x=b, is called a curvilinear trapezoid.

Ways to find the area of ​​a curvilinear trapezoid

Theorem. If f(x) is a continuous and non-negative function on the segment , then the area of ​​the corresponding curvilinear trapezoid is equal to the increment of antiderivatives.

Given: f(x) - continuous indefinitely. function, xO.

Prove: S = F(b) - F(a), where F(x) is the antiderivative of f(x).

Proof:

1) Consider the auxiliary function S(x). We assign to each xO that part of the curvilinear trapezoid, which lies to the left of the straight line (Fig. 2), passing through the point with this abscissa and parallel to the y-axis.

Hence S(a)=0 and S(b)=Str

Let us prove that S(a) is the antiderivative of f(x).

D(f) = D(S) =

S"(x0)= lim(S(x0+Dx) - S(x0) / Dx), for Dx®0 DS is a rectangle

Dx®0 with sides Dx and f(x0)

S "(x0) \u003d lim (Dx f (x0) / Dx) \u003d lim f (x0) \u003d f (x0): since x0 is a point, then S (x) -

Dx®0 Dx®0 antiderivative f(x).

Therefore, by the theorem on the general form of the antiderivative, S(x)=F(x)+C.

Because S(a)=0, then S(a) = F(a)+C

S = S(b)=F(b)+C = F(b)-F(a)

one). Let's divide the segment into n equal parts. Split step (Fig. 3)

Dx=(b-a)/n. In this case Str=lim(f(x0)Dx+f(x1)Dx+...+f(xn))Dx=n®Ґ = lim Dx(f(x0)+f(x1)+...+f (xn))

For n®Ґ we get that Str= Dx(f(x0)+f(x1)+...+f(xn))

The limit of this sum is called a definite integral.

The sum under the limit is called the integral sum.

The definite integral is the limit of the integral sum on the segment as n®Ґ. The integral sum is obtained as the limit of the sum of products of the length of the segment obtained by splitting the domain of the function at any point of this interval.

a - lower limit of integration;

b - top.

Newton-Leibniz formula.

Comparing the formulas for the area of ​​a curvilinear trapezoid, we conclude:

if F is the antiderivative of b on , then

f(x)dx = F(b)-F(a)

t f(x)dx = F(x) f = F(b) - F(a)

Properties of a definite integral.

t f(x)dx = t f(z)dz

t f(x)dx = F(a) - F(a) = 0

t f(x)dx = - t f(x)dx

t f(x)dx = F(a) - F(b) t f(x)dx = F(b) - F(a) = - (F(a) - F(b))

If a, b and c are any points of the interval I on which the continuous function f(x) has an antiderivative, then

t f(x)dx = t f(x)dx + t f(x)dx

F(b) - F(a) = F(c) - F(a) + F(b) - F(c) = F(b) - F(a)

(this is the additivity property of a definite integral)

If l and m are constants, then

t (lf(x) +m j(x))dx = l t f(x)dx + m tj(x))dx -

This is the linearity property of a definite integral.

t (f(x)+g(x)+...+h(x))dx = t f(x)dx+ t g(x)dx+...+ t h(x)dx

t (f(x)+g(x)+...+h(x))dx = (F(b) + G(b) +...+ H(b)) - (F(a) + G(a) +...+ H(a)) +C = F(b)-F(a)+C1 +G(b)-G(a)+C2+...+H(b)-H (a)+Cn=b b b = t f(x)dx+ t g(x)dx+...+ t h(x)dx

A set of standard pictures (Fig. 4, 5, 6, 7, 8)

Rice. four

Rice. 6 Rice. 7

Because f(x)<0, то формулу Ньютона-Лейбница составить нельзя, теорема верна только для f(x)і0.

It is necessary: ​​to consider the symmetry of the function with respect to the OX axis. ABCD®A"B"CD b

S (ABCD) \u003d S (A "B" CD) \u003d t -f (x) dx

S= t f(x)dx = t g(x)dx

S = t(f(x)-g(x))dx+t(g(x)-f(x))dx

S= t (f(x)+m-g(x)-m)dx =

t (f(x)-g(x))dx

t ((f(x)-g(x))dx

S= t (f(x)+m-g(x)-m)dx =

T (f(x)- g(x))dx

If on the segment f(x)іg(x), then the area between these graphs is equal to

t ((f(x)-g(x))dx

The functions f(x) and g(x) are arbitrary and non-negative

S=t f(x)dx - t g(x)dx = t (f(x)-g(x))dx

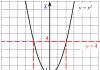
The figure bounded by the graph of a continuous non-negative function $f(x)$ on the interval $$ and the lines $y=0, \ x=a$ and $x=b$ is called a curvilinear trapezoid.

The area of ​​the corresponding curvilinear trapezoid is calculated by the formula:

$S=\int\limits_(a)^(b)(f(x)dx).$ (*)

The problems of finding the area of ​​a curvilinear trapezoid we will conditionally divide into $4$ types. Let's consider each type in more detail.

Type I: a curvilinear trapezoid is given explicitly. Then immediately apply the formula (*).

For example, find the area of ​​a curvilinear trapezoid bounded by the graph of the function $y=4-(x-2)^(2)$ and the lines $y=0, \ x=1$ and $x=3$.

Let's draw this curvilinear trapezoid.

Applying the formula (*), we find the area of ​​this curvilinear trapezoid.

$S=\int\limits_(1)^(3)(\left(4-(x-2)^(2)\right)dx)=\int\limits_(1)^(3)(4dx)- \int\limits_(1)^(3)((x-2)^(2)dx)=4x|_(1)^(3) – \left.\frac((x-2)^(3) )(3)\right|_(1)^(3)=$

$=4(3-1)-\frac(1)(3)\left((3-2)^(3)-(1-2)^(3)\right)=4 \cdot 2 - \frac (1)(3)\left((1)^(3)-(-1)^(3)\right) = 8 – \frac(1)(3)(1+1) =$

$=8-\frac(2)(3)=7\frac(1)(3)$ (unit$^(2)$).

Type II: curvilinear trapezoid is given implicitly. In this case, the straight lines $x=a, \ x=b$ are usually not specified or are partially specified. In this case, you need to find the intersection points of the functions $y=f(x)$ and $y=0$. These points will be the points $a$ and $b$.

For example, find the area of ​​the figure bounded by the graphs of the functions $y=1-x^(2)$ and $y=0$.

Let's find the intersection points. To do this, we equate the right parts of the functions.

So $a=-1$ and $b=1$. Let's draw this curvilinear trapezoid.

Find the area of ​​this curvilinear trapezoid.

$S=\int\limits_(-1)^(1)(\left(1-x^(2)\right)dx)=\int\limits_(-1)^(1)(1dx)-\int \limits_(-1)^(1)(x^(2)dx)=x|_(-1)^(1) – \left.\frac(x^(3))(3)\right|_ (-1)^(1)=$

$=(1-(-1))-\frac(1)(3)\left(1^(3)-(-1)^(3)\right)=2 – \frac(1)(3) \left(1+1\right) = 2 – \frac(2)(3) = 1\frac(1)(3)$ (unit$^(2)$).

Type III: the area of ​​a figure bounded by the intersection of two continuous non-negative functions. This figure will not be a curvilinear trapezoid, which means that using the formula (*) you cannot calculate its area. How to be? It turns out that the area of ​​this figure can be found as the difference between the areas of curvilinear trapezoids bounded by the upper function and $y=0$ ($S_(uf)$) and the lower function and $y=0$ ($S_(lf)$), where the role of $x=a, \ x=b$ is played by the $x$ coordinates of the intersection points of these functions, i.e.

$S=S_(uf)-S_(lf)$. (**)

The most important thing when calculating such areas is not to “miss” with the choice of the upper and lower functions.

For example, find the area of ​​a figure bounded by the functions $y=x^(2)$ and $y=x+6$.

Let's find the intersection points of these graphs:

According to Vieta's theorem,

$x_(1)=-2, \ x_(2)=3.$

That is, $a=-2, \ b=3$. Let's draw a figure:

So the top function is $y=x+6$ and the bottom one is $y=x^(2)$. Next, find $S_(uf)$ and $S_(lf)$ using the formula (*).

$S_(uf)=\int\limits_(-2)^(3)((x+6)dx)=\int\limits_(-2)^(3)(xdx)+\int\limits_(-2 )^(3)(6dx)=\left.\frac(x^(2))(2)\right|_(-2)^(3) + 6x|_(-2)^(3)= 32 ,5$ (unit $^(2)$).

$S_(lf)=\int\limits_(-2)^(3)(x^(2)dx)=\left.\frac(x^(3))(3)\right|_(-2) ^(3) = \frac(35)(3)$ (unit$^(2)$).

Substitute found in (**) and get:

$S=32,5-\frac(35)(3)= \frac(125)(6)$ (unit $^(2)$).

Type IV: the area of ​​a figure bounded by a function(s) that does not satisfy the non-negativity condition. In order to find the area of ​​such a figure, you need to be symmetrical about the $Ox$ axis ( in other words, put “minuses” in front of the functions) display the area and, using the methods described in types I - III, find the area of ​​the displayed area. This area will be the required area. First, you may have to find the intersection points of the function graphs.

For example, find the area of ​​the figure bounded by the graphs of the functions $y=x^(2)-1$ and $y=0$.

Let's find the intersection points of the function graphs:

those. $a=-1$ and $b=1$. Let's draw the area.

Let's display the area symmetrically:

$y=0 \ \Rightarrow \ y=-0=0$

$y=x^(2)-1 \ \Rightarrow \ y= -(x^(2)-1) = 1-x^(2)$.

You get a curvilinear trapezoid bounded by the graph of the function $y=1-x^(2)$ and $y=0$. This is a problem of finding a curvilinear trapezoid of the second type. We already solved it. The answer was: $S= 1\frac(1)(3)$ (units $^(2)$). So, the area of ​​the desired curvilinear trapezoid is equal to:

$S=1\frac(1)(3)$ (unit$^(2)$).

This term has other meanings, see Trapezium (meanings). Trapeze (from other Greek τραπέζιον "table"; ... Wikipedia

I Area is one of the basic quantities associated with geometric shapes. In the simplest cases, it is measured by the number of unit squares filling a flat figure, that is, squares with a side equal to one length. Calculation P. ... ...

Methods for obtaining numerical solutions of various problems by means of graphic constructions. G. c. (graphical multiplication, graphical solution of equations, graphical integration, etc.) represent a system of constructions that repeat or replace ... ... Great Soviet Encyclopedia

Area, one of the basic quantities associated with geometric shapes. In the simplest cases, it is measured by the number of unit squares filling a flat figure, that is, squares with a side equal to one length. The calculation of P. was already in antiquity ... ... Great Soviet Encyclopedia

Green's theorem establishes a connection between a curvilinear integral over a closed contour C and a double integral over a region D bounded by this contour. In fact, this theorem is a special case of the more general Stokes theorem. The theorem is named in ... Wikipedia

Section 4.3 it has already been noted that definite integral () of

non-negative function is numerically equal to the area of ​​a curvilinear trapezoid bounded by the graph of the function = (), straight lines = , = and = 0.

Example 4.24. Calculate the area of ​​\u200b\u200bthe figure enclosed between the axis and the sinusoid \u003d sin, (figure 4.6).

If the figure is not a curvilinear trapezoid, then they try to represent its area as the sum or difference of the areas of figures that are curvilinear trapezoids. In particular, the theorem is true.

Theorem 4.13. If the figure is bounded from above and below by graphs of continuous functions = 1 (), = 2 () (not necessarily non-negative, ( figure 4.7 ), then its area can be found by the formula

2 () − 1 () .

Example 4.25. Calculate the area of ​​a figure bounded by a curve = 4 and straight lines = and = 4.

Part I. Theory

Chapter 4. Integration Theory 4.4. Applications of the integral. Improper integrals

4.4.2. Curve arc length

The calculation of curve lengths also leads to integrals. Let the function = () be continuous on the segment [ ; ] and is differentiable on the interval (;). Its graph represents some curve, (; ()), (; ()) (figure 4.9). We divide the curve with points 0 = , 1 , 2 , . . . , = on arbitrary parts. Let's connect two neighboring points −1 and by chords,= 1, 2, . . . , . We get a -link broken line inscribed in the curve. Let

is the length of the chord −1 , = 1, 2, . . . , = max16 6 . The length of the polyline will be expressed by the formula

It is natural to define the length of a curve as the limiting value of the lengths of broken lines when → 0, i.e.

Then the coordinates of the points are (; ()), and, using formula for the distance between two points, find

Therefore, there is an integral sum for the function √ 1 + (′ ())2 on the interval [ ; ]. Then on the basis of equalities (4.31) we have:

Solution. Let's build a graph of the specified function (figure 4.10).

Figure 4.10

Back forward

Attention! The slide preview is for informational purposes only and may not represent the full extent of the presentation. If you are interested in this work, please download the full version.

Keywords: integral, curvilinear trapezoid, area of ​​figures bounded by lilies

Equipment: whiteboard, computer, multimedia projector

Lesson type: lesson-lecture

Lesson Objectives:

• educational: to form a culture of mental work, to create a situation of success for each student, to form a positive motivation for learning; develop the ability to speak and listen to others.
• developing: the formation of the independence of the student's thinking in the application of knowledge in various situations, the ability to analyze and draw conclusions, the development of logic, the development of the ability to correctly pose questions and find answers to them. Improving the formation of computational, calculating skills, developing the thinking of students in the course of performing the proposed tasks, developing an algorithmic culture.
• educational: to form concepts about a curvilinear trapezoid, about an integral, to master the skills of calculating the areas of flat figures

Teaching method: explanatory and illustrative.

During the classes

In the previous classes, we learned how to calculate the areas of figures whose boundaries are broken lines. In mathematics, there are methods that allow you to calculate the area of ​​\u200b\u200bfigures bounded by curves. Such figures are called curvilinear trapezoids, and their area is calculated using antiderivatives.

Curvilinear trapezoid ( slide 1)

A curvilinear trapezoid is a figure bounded by the function graph, ( w.m.), straight x = a and x = b and abscissa

Various types of curvilinear trapezoids ( slide 2)

We consider various types of curvilinear trapezoids and notice: one of the lines is degenerate into a point, the role of the limiting function is played by the line

Area of ​​a curvilinear trapezoid (slide 3)

Fix the left end of the interval a, and right X we will change, i.e., we move the right wall of the curvilinear trapezoid and get a changing figure. The area of ​​a variable curvilinear trapezoid bounded by the function graph is the antiderivative F for function f

And on the segment [ a; b] the area of ​​the curvilinear trapezoid formed by the function f, is equal to the increment of the antiderivative of this function:

Exercise 1:

Find the area of ​​a curvilinear trapezoid bounded by the graph of a function: f(x) = x 2 and direct y=0, x=1, x=2.

Solution: ( according to the slide 3 algorithm)

Draw a graph of the function and lines

Find one of the antiderivatives of the function f(x) = x 2 :

Slide Self-Check

Integral

Consider a curvilinear trapezoid given by the function f on the segment [ a; b]. Let's break this segment into several parts. The area of ​​the entire trapezoid will be divided into the sum of the areas of smaller curvilinear trapezoids. ( slide 5). Each such trapezoid can be approximately considered a rectangle. The sum of the areas of these rectangles gives an approximate idea of ​​the entire area of ​​the curvilinear trapezoid. The smaller we break the segment [ a; b], the more accurately we calculate the area.

We write these considerations in the form of formulas.

Divide the segment [ a; b] into n parts with dots x 0 \u003d a, x1, ..., xn \u003d b. Length k- th denote by xk = xk - xk-1. Let's sum up

Geometrically, this sum is the area of ​​the figure shaded in the figure ( sh.m.)

Sums of the form are called integral sums for the function f. (sch.m.)

Integral sums give an approximate value of the area. The exact value is obtained by passing to the limit. Imagine that we refine the partition of the segment [ a; b] so that the lengths of all small segments tend to zero. Then the area of ​​the composed figure will approach the area of ​​the curvilinear trapezoid. We can say that the area of ​​a curvilinear trapezoid is equal to the limit of integral sums, Sk.t. (sch.m.) or integral, i.e.,

Definition:

function integral f(x) from a before b is called the limit of integral sums

= (sch.m.)

Newton-Leibniz formula.

Remember that the limit of integral sums is equal to the area of ​​a curvilinear trapezoid, so we can write:

Sk.t. = (sch.m.)

On the other hand, the area of ​​a curvilinear trapezoid is calculated by the formula

S to. t. (sch.m.)

Comparing these formulas, we get:

This equality is called the Newton-Leibniz formula.

For the convenience of calculations, the formula is written as:

Tasks: (sch.m.)

1. Calculate the integral using the Newton-Leibniz formula: ( check slide 5)

2. Compile integrals according to the drawing ( check on slide 6)

3. Find the area of ​​​​a figure bounded by lines: y \u003d x 3, y \u003d 0, x \u003d 1, x \u003d 2. ( Slide 7)

Finding the areas of plane figures ( slide 8)

How to find the area of ​​figures that are not curvilinear trapezoids?

Let two functions be given, the graphs of which you see on the slide . (sch.m.) Find the area of ​​the shaded figure . (sch.m.). Is the figure in question a curvilinear trapezoid? And how can you find its area, using the additivity property of the area? Consider two curvilinear trapezoids and subtract the area of ​​the other from the area of ​​one of them ( w.m.)

Let's make an algorithm for finding the area from the animation on the slide:

1. Plot Functions
2. Project the intersection points of the graphs onto the x-axis
3. Shade the figure obtained by crossing the graphs
4. Find curvilinear trapezoids whose intersection or union is the given figure.
5. Calculate the area of ​​each
6. Find difference or sum of areas

Oral task: How to get the area of ​​a shaded figure (tell using animation, slide 8 and 9)

Homework: Work out the abstract, No. 353 (a), No. 364 (a).

Bibliography

1. Algebra and the beginning of analysis: a textbook for grades 9-11 of the evening (shift) school / ed. G.D. Glaser. - M: Enlightenment, 1983.
2. Bashmakov M.I. Algebra and the beginning of analysis: a textbook for grades 10-11 of middle school / Bashmakov M.I. - M: Enlightenment, 1991.
3. Bashmakov M.I. Mathematics: a textbook for institutions beginning. and avg. prof. education / M.I. Bashmakov. - M: Academy, 2010.
4. Kolmogorov A.N. Algebra and the beginning of analysis: a textbook for 10-11 cells. educational institutions / A.N. Kolmogorov. - M: Enlightenment, 2010.
5. Ostrovsky S.L. How to make a presentation for the lesson? / S.L. Ostrovsky. – M.: First of September, 2010.