Historia del origen de la teoría de grafos. Historia del surgimiento y desarrollo de la teoría de grafos. Teoría de grafos y los problemas aplicados modernos más importantes.

GRÁFICOS

Muchos problemas se reducen a considerar un conjunto de objetos cuyas propiedades esenciales se describen mediante las conexiones entre ellos. Por ejemplo, al mirar un mapa de carreteras, es posible que uno sólo esté interesado en si existe una conexión entre ciertos asentamientos, ignorando la configuración y calidad de las carreteras, las distancias y otros detalles. Al estudiar circuitos eléctricos, puede pasar a primer plano la naturaleza de las conexiones de sus distintos componentes: resistencias, condensadores, fuentes, etc. Las moléculas orgánicas forman estructuras cuyas propiedades características son las conexiones entre átomos. Pueden ser de interés diversas conexiones y relaciones entre personas, eventos, estados y, en general, entre cualquier objeto.

En tales casos, es conveniente representar los objetos considerados como puntos y las conexiones entre ellos como líneas de configuración arbitraria. Una imagen tan formalizada se llama gráfico (del griego grajw - escribo).

Arroz. 4.1 .

El primer trabajo sobre gráficos fue publicado por Leonhard Euler, de veinte años, en 1736, mientras trabajaba en la Academia de Ciencias de Rusia. Contenía una solución al problema de los puentes de Königsberg (Fig. 4.1a): ¿es posible dar un paseo de tal manera que, saliendo de cualquier lugar de la ciudad, se pueda regresar a él caminando exactamente una vez sobre cada puente? ? Está claro que, según las condiciones del problema, no importa cómo pasa el camino por las partes del terreno a, b, c, d, en las que se encuentra la ciudad de Koenigsberg (ahora Kaliningrado), por lo que pueden ser representados como vértices. Y dado que las conexiones entre estas partes se realizan solo a través de siete puentes, cada uno de ellos está representado por una arista que conecta los vértices correspondientes. Como resultado, obtenemos el gráfico que se muestra en la Fig. 4.1b. Euler dio una respuesta negativa a la pregunta planteada. Además, demostró que tal ruta existe sólo para un gráfico tal que cada uno de sus vértices está conectado a un número par de aristas.

La teoría de grafos recibió su siguiente impulso casi 100 años después con el desarrollo de la investigación en redes eléctricas, cristalografía, química orgánica y otras ciencias. Además de numerosos acertijos y juegos de gráficos, se consideraron importantes problemas prácticos, muchos de los cuales requerían sofisticadas técnicas matemáticas. Ya a mediados del siglo pasado, Kirchhoff utilizó gráficos para analizar circuitos eléctricos y Cayley exploró una clase importante de gráficos para identificar y enumerar isómeros de hidrocarburos saturados. Sin embargo, la teoría de grafos como disciplina matemática se formó recién a mediados de los años treinta del siglo pasado gracias al trabajo de muchos investigadores, el mayor mérito de los cuales pertenece a D. Koenig. Los científicos soviéticos L. S. Pontryagin, A. A. Zykov, V. G. Vising y otros hicieron importantes contribuciones a la teoría de grafos.

Sin siquiera darnos cuenta, nos encontramos con gráficos todo el tiempo. Por ejemplo, una gráfica es un diagrama de líneas de metro. Los puntos representan estaciones y las líneas representan rutas de tren. Al investigar nuestra ascendencia y rastrearla hasta nuestros antepasados, construimos un árbol genealógico. Y este árbol es un gráfico.

Los gráficos sirven como un medio conveniente para describir relaciones entre objetos. Por ejemplo, al considerar un gráfico que representa una red de carreteras entre áreas pobladas, puede determinar la ruta desde el punto A al punto B. Si hay varias rutas de este tipo, le gustaría elegir la óptima en cierto sentido, por ejemplo el más corto o el más seguro. Para resolver el problema de selección es necesario realizar ciertos cálculos sobre gráficas. Al resolver este tipo de problemas, es conveniente utilizar técnicas algebraicas y es necesario formalizar el concepto mismo de gráfico.

La teoría de grafos tiene una herramienta poderosa para resolver problemas aplicados de una amplia variedad de campos de la ciencia y la tecnología. Esto incluye, por ejemplo, el análisis y síntesis de circuitos y sistemas, el diseño de canales de comunicación y el estudio de procesos de transferencia de información, la construcción de circuitos de contacto y el estudio de máquinas de estados finitos, la planificación y el control de redes, la investigación de operaciones, la selección de rutas y flujos óptimos en redes, estudio de procesos aleatorios y muchas otras tareas. La teoría de grafos está estrechamente relacionada con ramas de las matemáticas discretas como la teoría de conjuntos, la teoría de matrices, la lógica matemática y la teoría de la probabilidad.

Actualmente, la teoría de grafos cubre mucho material, pero al presentarla nos limitaremos solo a una parte y, omitiendo numerosos teoremas, consideraremos solo unos pocos. conceptos básicos.

Leonard Euler es considerado el fundador de la teoría de grafos. En 1736, en una de sus cartas, formuló y propuso una solución al problema de los siete puentes de Königsberg, que más tarde se convirtió en uno de los problemas clásicos de la teoría de grafos.

Los primeros problemas de la teoría de grafos estaban relacionados con la resolución de problemas y acertijos matemáticos recreativos. Aquí hay un recuento de un extracto de la carta de Euler del 13 de marzo de 1736: “Me dieron un problema sobre una isla ubicada en la ciudad de Königsberg y rodeada por un río con siete puentes que la cruzan. La cuestión es si alguien puede rodearlos continuamente, pasando sólo una vez por cada puente. Y luego me informaron que nadie había podido hacer esto todavía, pero nadie había demostrado que fuera imposible. Esta cuestión, aunque trivial, me pareció, sin embargo, digna de atención en el sentido de que ni la geometría, ni el álgebra, ni el arte combinatorio son suficientes para resolverla. Después de mucho pensar, encontré una regla fácil, basada en una prueba completamente convincente, con la ayuda de la cual es posible, en todos los problemas de este tipo, determinar inmediatamente si tal desvío se puede hacer a través de cualquier número y cualquier número de puentes ubicados de cualquier forma o no”. Los puentes de Königsberg se pueden representar esquemáticamente de la siguiente manera:

Regla de Euler:

1. En un gráfico que no tiene vértices de grados impares, hay un recorrido de todas las aristas (y cada arista se atraviesa exactamente una vez) comenzando en cualquier vértice del gráfico.

2. En un gráfico que tiene dos y sólo dos vértices de grado impar, hay un recorrido que comienza en un vértice de grado impar y termina en el otro.

3. En un gráfico que tiene más de dos vértices con grados impares, dicho recorrido no existe.

Existe otro tipo de problema relacionado con viajar a lo largo de gráficos. Estamos hablando de problemas en los que es necesario encontrar un camino que pase por todos los vértices, y no más de una vez por cada uno. Un ciclo que pasa por cada vértice una y sólo una vez se llama línea hamiltoniana (en honor a William Rowan Hamilton, el famoso matemático irlandés del siglo pasado que fue el primero en estudiar tales líneas). Desafortunadamente, todavía no se ha encontrado un criterio general con el que se pueda decidir si una gráfica dada es hamiltoniana y, de ser así, encontrar todas las rectas hamiltonianas en ella.

Formulado a mediados del siglo XIX. El problema de los cuatro colores también parece un problema entretenido, pero los intentos de resolverlo han llevado a algunos estudios de gráficos que tienen importancia teórica y aplicada. El problema de los cuatro colores se formula de la siguiente manera: "¿Se puede colorear un área de cualquier mapa plano con cuatro colores de modo que dos áreas adyacentes cualesquiera se coloreen con colores diferentes?" La hipótesis de que la respuesta es afirmativa se formuló a mediados del siglo XIX. En 1890 se demostró una afirmación más débil: cualquier mapa plano se puede colorear con cinco colores. Al asociar cualquier mapa plano con su gráfico plano dual, obtenemos una formulación equivalente del problema en términos de gráficos: ¿Es cierto que el número cromático de cualquier gráfico plano es menor o igual a cuatro? Numerosos intentos de resolver el problema influyeron en el desarrollo de varias áreas de la teoría de grafos. En 1976 se anunció una solución positiva al problema utilizando una computadora.

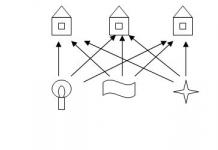
Otro viejo problema topológico que durante mucho tiempo ha sido particularmente difícil de resolver y que ha atormentado las mentes de los amantes de los rompecabezas es el conocido como "problema del suministro de electricidad, gas y agua". En 1917, Henry E. Dudeney le dio esta formulación. Se debe instalar gas, electricidad y agua en cada una de las tres casas que se muestran en la figura.

Teoría de grafos. 1

La historia del surgimiento de la teoría de grafos. 1

La regla de Euler. 1

Literatura

1. Teoría de grafos de Belov, Moscú, "Ciencia", 1968.

2. Nuevas tecnologías pedagógicas y de la información E.S. Polat , Moscú, "Academia" 1999

3. Kuznetsov O.P., Adelson-Velsky G.M. Matemáticas discretas para el ingeniero. – M.: Energoatomizdat, 1988.

4. Cook D., Baze G. Matemáticas informáticas. – M.: Ciencia, 1990.

5. Nefedov V.N., Osipova V.A. Curso de matemáticas discretas. – M.: Editorial MAI, 1992.

6. Ore O. Teoría de grafos. – M.: Ciencia, 1980.

7. Ismagilov R.S., Kalinkin A.V. Materiales para las lecciones prácticas del curso: Matemática Discreta

Teoría de grafos- capítulo Matemáticas discretas, estudiando propiedades graficos . En un sentido general, un gráfico se representa como un conjunto de vértices (nodos) conectados por aristas. En una definición estricta, ese par de conjuntos se llama gráfico. G=(V,E), donde V es un subconjunto de cualquier conjunto contable y E es un subconjunto de V×V.

Historia de la teoría de grafos
Leonard Euler es considerado el fundador de la teoría de grafos. En 1736, en una de sus cartas, formuló y propuso una solución al problema de los siete puentes de Königsberg, que más tarde se convirtió en uno de los problemas clásicos de la teoría de grafos.
Los primeros problemas de la teoría de grafos estaban relacionados con la resolución de problemas y acertijos matemáticos recreativos. Aquí hay un recuento de un extracto de la carta de Euler del 13 de marzo de 1736: “Me dieron un problema sobre una isla ubicada en la ciudad de Königsberg y rodeada por un río con siete puentes que la cruzan. La cuestión es si alguien puede rodearlos continuamente, pasando sólo una vez por cada puente. Y luego me informaron que nadie había podido hacer esto todavía, pero nadie había demostrado que fuera imposible. Esta cuestión, aunque trivial, me pareció, sin embargo, digna de atención en el sentido de que ni la geometría, ni el álgebra, ni el arte combinatorio son suficientes para resolverla. Después de mucho pensar, encontré una regla fácil, basada en una prueba completamente convincente, con la ayuda de la cual es posible, en todos los problemas de este tipo, determinar inmediatamente si tal desvío se puede hacer a través de cualquier número y cualquier número de puentes ubicados de cualquier forma o no”. Los puentes de Königsberg se pueden representar esquemáticamente de la siguiente manera:
Regla de Euler:

1. En un gráfico que no tiene vértices de grados impares, hay un recorrido de todas las aristas (y cada arista se recorre exactamente una vez) comenzando en cualquier vértice del gráfico.
2. En un gráfico que tiene dos y sólo dos vértices de grado impar, hay un recorrido que comienza en un vértice de grado impar y termina en el otro.
3. En un gráfico que tiene más de dos vértices con grados impares, dicho recorrido no existe.

año escolar 2016 Año

1. Introducción

2. Historia del surgimiento de la teoría de grafos.

3. Conceptos básicos de la teoría de grafos.

4. Teoremas básicos de la teoría de grafos

5. Métodos para representar gráficos en una computadora.

6. Repaso de problemas de teoría de grafos.

7. Conclusión

8. Referencias

Introducción

Recientemente, la investigación en áreas tradicionalmente relacionadas con las matemáticas discretas se ha vuelto cada vez más prominente. Junto con secciones clásicas de matemáticas como análisis matemático y ecuaciones diferenciales, en los planes de estudios de la especialidad "Matemáticas Aplicadas" y muchas otras especialidades han aparecido secciones sobre lógica matemática, álgebra, combinatoria y teoría de grafos. Las razones de esto no son difíciles de entender, simplemente identificando la variedad de problemas resueltos sobre la base de este aparato matemático.

La historia del surgimiento de la teoría de grafos.

1. Problema con los puentes de Königsberg. En la Fig. 1 muestra un plano esquemático de la parte central de la ciudad de Koenigsberg (ahora Kaliningrado), incluidas dos orillas del río Pérgola, dos islas y siete puentes de conexión. La tarea consiste en rodear las cuatro partes del terreno, cruzar cada puente una vez y regresar al punto de partida. Este problema fue resuelto (se demostró que no había solución) por Euler en 1736.

arroz. 1

2. El problema de las tres casas y los tres pozos. Hay tres casas y tres pozos, de alguna manera ubicados en un plano. Dibuje un camino desde cada casa hasta cada pozo para que los caminos no se crucen (Fig. 2). Este problema fue resuelto (se demostró que no hay solución) por Kuratovsky en 1930.

arroz. 2

3. El problema de los cuatro colores. La división de un plano en áreas que no se superponen se llama mapa. Las áreas de un mapa se denominan adyacentes si tienen un borde común. La tarea consiste en colorear el mapa de tal manera que no haya dos áreas adyacentes pintadas del mismo color (Fig. 3). Desde finales del siglo pasado se conoce la hipótesis de que cuatro colores son suficientes para ello. En 1976, Appel y Heiken publicaron una solución al problema de los cuatro colores, que se basaba en una búsqueda por ordenador. La solución a este problema “programáticamente” sentó un precedente que dio lugar a una acalorada discusión que de ninguna manera ha terminado. La esencia de la solución publicada es probar un número grande pero finito (alrededor de 2000) tipos de posibles contraejemplos del teorema de los cuatro colores y demostrar que ni un solo caso es un contraejemplo. El programa completó esta búsqueda en aproximadamente mil horas de funcionamiento de la supercomputadora. Es imposible comprobar la solución resultante "manualmente": el alcance de la enumeración va mucho más allá de las capacidades humanas. Muchos matemáticos plantean la pregunta: ¿puede considerarse válida una “demostración de programa” de este tipo? Después de todo, puede haber errores en el programa... Los métodos para demostrar formalmente la corrección de los programas no son aplicables a programas de tal complejidad como el que se está discutiendo. Las pruebas no pueden garantizar la ausencia de errores y, en este caso, generalmente son imposibles. Por lo tanto, sólo podemos confiar en las habilidades de programación de los autores y creer que hicieron todo bien.

Arroz. 3

Conceptos básicos de la teoría de grafos.

1) Gráfica G(V,E) es una colección de dos conjuntos: un conjunto no vacío V (conjunto de vértices) y un conjunto E de subconjuntos de dos elementos del conjunto V (E – conjunto de aristas).

2) Orientado es un gráfico en el que hay un conjunto de pares ordenados de vértices de la forma (x,y), donde x se llama comienzo e y es el final del arco. El arco (x, y) a menudo se escribe como . También dicen que el arco va del vértice x al vértice y, y el vértice y adyacente con vértice x.

3) Si un elemento del conjunto E puede ser un par idéntico elementos (no distintos) de V, entonces dicho elemento del conjunto E se llama bucle, y la gráfica se llama grafico con bucles(o pseudografo).

4) Si E no es un conjunto, pero colocar que contiene varios elementos idénticos, entonces estos elementos se llaman múltiples bordes, y la gráfica se llama multigrafo.

5) Si los elementos del conjunto E no son necesariamente de dos elementos, sino cualquier subconjunto del conjunto V, entonces dichos elementos del conjunto E se llaman hiperarcos, y la gráfica se llama hipergrafo.

6) Si se especifica la función F: V → METRO y/o F: mi → METRO, entonces el conjunto METRO llamado un conjunto notas, y la gráfica se llama marcado(o cargado). El conjunto de marcas suele ser letras o números enteros. Si la función F es inyectivo, es decir, diferentes vértices (aristas) tienen diferentes etiquetas, entonces el gráfico se llama numerado.

7) Subgrafo se llama gráfico G′(V′,E′), donde y/o .

a) Si V′ = V, entonces G′ se llama centro subgrafo G.

b) Si , entonces la gráfica G′ se llama propio subgrafo del gráfico G.

c) Un subgrafo G′(V′,E′) se llama subgrafo regular del grafo G(V,E) si G′ contiene todas las aristas posibles de G.

8) Grado (valencia) vértices es el número de aristas incidentes en este vértice (el número de vértices adyacentes a él).

9) Ruta en un gráfico es una secuencia alterna de vértices y aristas en la que inciden dos elementos adyacentes cualesquiera.

a) Si , entonces la ruta cerrado, de lo contrario abierto.

b) Si todos los bordes son diferentes, entonces la ruta se llama cadena.

c) Si todos los vértices (y por lo tanto las aristas) son diferentes, entonces la ruta se llama cadena sencilla.

d) Un circuito cerrado se llama ciclo.

e) Un circuito simple cerrado se llama bucle simple.

f) Una gráfica sin ciclos se llama acíclico.

g) Para dígrafos, la cadena se llama por, y el ciclo es describir.

arroz. 4. Rutas, cadenas, ciclos

Ejemplo

En el gráfico, cuyo diagrama se muestra en la Fig.4:

1. v 1, v 3, v 1, v 4 – una ruta, pero no un circuito;

2. v 1, v 3, v 5, v 2, v 3, v 4 – una cadena, pero no una cadena simple;

3. v 1, v 4, v 3, v 2, v 5 – cadena simple;

4. v 1, v 3, v 5, v 2, v 3, v 4, v 1 – un ciclo, pero no un ciclo simple;

5. v 1, v 3, v 4, v 1 – un ciclo simple.

10) Si un gráfico tiene un ciclo (no necesariamente simple) que contiene todos los bordes del gráfico una vez, entonces dicho ciclo se llama Euleriano ciclo.

11) Si un gráfico tiene un ciclo simple que contiene todos los vértices del gráfico (uno a la vez), entonces dicho ciclo se llama hamiltoniano ciclo.

12) árbol llamado gráfico conexo sin ciclos.

13) esqueleto Se llama un árbol que contiene todos los vértices de un gráfico.

14) Pareo es un conjunto de aristas en las que no hay dos adyacentes.

15) El emparejamiento se llama máximo, si ningún superconjunto del mismo es independiente.

16) Dos vértices en un gráfico conectado, si hay una cadena simple que los conecta.

17) Un gráfico en el que todos los vértices están conectados se llama coherente.

18) Un gráfico que consta únicamente de vértices aislados se llama bastante incoherente.

19) Longitud de la ruta se llama el número de aristas que contiene (con repeticiones).

20) Distancia entre los vértices u y v se llama longitud de la cadena más corta, y la cadena más corta en sí se llama geodésico.

21) Diámetro de un gráfico G se llama longitud de la geodésica más larga.

22) Excentricidad El vértice v en un gráfico conectado G (V, E) es la distancia máxima desde el vértice v a otros vértices del gráfico G.

23) Radio de un gráfico G se llama la más pequeña de las excentricidades de los vértices.

24) El vértice v se llama central, si su excentricidad coincide con el radio de la gráfica.

25) El conjunto de vértices centrales se llama centro grafico.

arroz. 5 Excentricidades de vértices y centros de gráficas (resaltadas).

Información relacionada.

La teoría de grafos encuentra aplicación, por ejemplo, en los sistemas de información geográfica (SIG). Las casas, estructuras, bloques, etc. existentes o de nuevo diseño se consideran vértices, y las carreteras, redes de servicios públicos, líneas eléctricas, etc. que los conectan se consideran bordes. El uso de diversos cálculos realizados en dicho gráfico permite, por ejemplo, encontrar la ruta de desvío más corta o la tienda de comestibles más cercana, o planificar la ruta óptima.

La teoría de grafos contiene una gran cantidad de problemas sin resolver e hipótesis aún no probadas.

Historia de la teoría de grafos

Leonard Euler es considerado el fundador de la teoría de grafos. En 1736, en una de sus cartas, formuló y propuso una solución al problema de los siete puentes de Königsberg, que más tarde se convirtió en uno de los problemas clásicos de la teoría de grafos. El término "gráfico" fue acuñado por primera vez por Sylvester, James Joseph en 1878 en su artículo en Nature [ ] .

Terminología de la teoría de grafos

Aplicación de la teoría de grafos

ver también

Notas

Literatura

• Distel R. Teoría de grafos Trans. De inglés - Novosibirsk: Editorial del Instituto de Matemáticas, 2002. - 336 p. ISBN 5-86134-101-X.
• Diestel R. Teoría de grafos, edición electrónica. - Nueva York: Springer-Verlag, 2005. - P. 422.
• Basaker R., Saati T. Grafos finitos y redes. M.: Nauka, 1974. 368c.
• Belov V.V., Vorobiev E.M., Shatalov V.E. Teoría de grafos. - M.: Más alto. escuela, 1976. - P. 392.
• Bergé K. Teoría de grafos y sus aplicaciones. M.: Illinois, 1962. 320c.
• Emelichev V. A., Melnikov O. I., Sarvanov V. I., Tyshkevich R. I. Conferencias sobre teoría de grafos. M.: Nauka, 1990. 384 p. (Ed. 2, M. revisado: URSS, 2009. 392 p.)