Istituzione educativa di bilancio comunale

Scuola media Doschatinskaja

distretto urbano di Vyksa, regione di Nizhny Novgorod

Risoluzione di problemi logici.

Dipartimento di Fisica e Matematica

Sezione matematica

Ho fatto il lavoro:

Studente di quinta elementare

Papotina Elena Sergeevna

consulente scientifico:

insegnante MBOU Doschatinskaya Scuola Secondaria

Roshchina Lyudmila Valerievna

Regione di Nižnij Novgorod

r/p Doschatoe

2016

annotazione

Lo scopo di questo lavoroidentificare la capacità di ragionare e trarre conclusioni corrette quando si risolvono problemi logici.QuestiI problemi sono divertenti e non richiedono molte conoscenze matematiche, quindi attirano anche quegli studenti a cui non piace molto la matematica.L'opera ha i seguenti compiti:

1) familiarità con i concetti di “logica” e “logica matematica”;

2) studio dei metodi di base per la risoluzione di problemi logici;

3) studiare la capacità di risolvere problemi logici da parte degli studenti delle classi 5-7.

I metodi di ricerca di questo lavoro sono:

Raccolta e studio delle informazioni.

Generalizzazione del materiale sperimentale e teorico.

Ipotesi : Gli studenti della nostra scuola sono in grado di risolvere problemi logici.

Durante la stesura dell'opera sono stati studiati tipi e metodi per risolvere problemi logici. È stato svolto un lavoro pratico con gli studenti delle scuole medie su come risolvere problemi logici. I risultati del lavoro hanno mostrato che non tutti gli studenti possono far fronte a compiti logici.Molto spesso, le capacità degli scolari rimangono nascoste, non hanno fiducia nelle proprie capacità e sono indifferenti alla matematica.Per tali studenti, propongo l'utilizzo di compiti logici. Questi compiti possono essere presi in considerazione nelle classi di club e opzionali.

2.3 Metodo del cerchio di Eulero

Questo metodoè un altro modo visivo e piuttosto interessante per risolvere problemi logici. Questo metodo si basa sulla costruzione dei famosi cerchi di Eulero-Venn,problemi in cui è necessario trovare qualche intersezione di insiemi o la loro unione, osservando le condizioni del problema. Diamo un'occhiata a un esempio di utilizzo di questo metodo.

Risolviamo il problema 6:

Dei 52 scolari, 23 collezionano badge, 35 raccolgono francobolli e 16 raccolgono sia badge che francobolli. Il resto non è interessato al collezionismo. Quanti scolari non sono interessati al collezionismo?

Soluzione. Le condizioni di questo problema non sono così facili da comprendere. Se si sommano 23 e 35 si ottiene più di 52. Ciò si spiega con il fatto che qui abbiamo contato due volte alcuni scolari, cioè quelli che collezionano sia badge che francobolli.Per facilitare la discussione utilizziamo i cerchi di Eulero

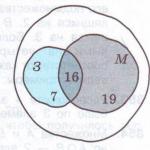
C'è un grande cerchio nella fotodenota i 52 studenti in questione; il cerchio 3 raffigura gli scolari che raccolgono distintivi, mentre il cerchio M raffigura gli scolari che raccolgono francobolli.

Il cerchio grande è diviso dai cerchi 3 e M in diverse aree. L'intersezione dei cerchi 3 e M corrisponde agli scolari che raccolgono sia badge che francobolli (Fig.). La parte del cerchio 3 che non appartiene al cerchio M corrisponde agli scolari che collezionano solo badge, e la parte del cerchio M che non appartiene al cerchio 3 corrisponde agli scolari che collezionano solo francobolli. La parte libera del cerchio grande rappresenta gli scolari che non sono interessati al collezionismo.

Compileremo in sequenza il nostro diagramma, inserendo in ogni area il numero corrispondente. Secondo la condizione, sia i badge che i francobolli vengono raccolti da 16 persone, quindi all'intersezione dei cerchi 3 e M scriveremo il numero 16 (Fig.).

Poiché 23 scolari raccolgono badge e 16 scolari raccolgono sia badge che francobolli, allora 23 - 16 = 7 persone raccolgono solo badge. Allo stesso modo solo i francobolli vengono collezionati da 35 - 16 = 19 persone. Scriviamo i numeri 7 e 19 nelle aree corrispondenti del diagramma.

Dalla foto è chiaro quante persone sono coinvolte nel collezionismo. Per scoprirlodevi aggiungere i numeri 7, 9 e 16. Otteniamo 42 persone. Ciò significa che 52 - 42 = 10 scolari continuano a non essere interessati al collezionismo. Questa è la risposta al problema; può essere inserita nel campo libero del grande cerchio.

Il metodo di Eulero è indispensabile per risolvere alcuni problemi e inoltre semplifica notevolmente il ragionamento.

2.4 Metodo dello schema a blocchi

Soluzione. Formalizziamo la soluzione sotto forma di diagramma a blocchi:

Risposta: 18 opzioni.

2.5 Problemi di verità

Chiameremo problemi di verità i problemi in cui è necessario stabilire la verità o la falsità delle affermazioni.

Problema 7 . Tre amici Kolya, Oleg e Petya stavano giocando nel cortile e uno di loro ha rotto accidentalmente il vetro della finestra con una palla. Kolya ha detto: "Non sono stato io a rompere il vetro". Oleg ha detto: "Petya ha rotto il vetro". Successivamente si scoprì che una di queste affermazioni era vera e l'altra falsa. Quale ragazzo ha rotto il vetro?

Soluzione. Supponiamo che Oleg abbia detto la verità, quindi anche Kolya abbia detto la verità, e questo contraddice le condizioni del problema. Di conseguenza, Oleg ha detto una bugia e Kolya ha detto la verità. Dalle loro dichiarazioni risulta che Oleg ha rotto il vetro.

Compito 8. Quattro studenti - Vitya, Petya, Yura e Sergei - hanno conquistato quattro primi posti alle Olimpiadi della matematica. Alla domanda su quali posti avessero preso, sono state date le seguenti risposte:

a) Petya - secondo, Vitya - terzo;

b) Sergey - secondo, Petya - primo;

c) Yura - secondo, Vitya - quarto.

Indica chi ha occupato quale posto se solo una parte di ciascuna risposta è corretta.

Soluzione. Supponiamo che l'affermazione "Pietro - II" sia vera, quindi entrambe le affermazioni della seconda persona sono errate e ciò contraddice le condizioni del problema. Supponiamo che l'affermazione "Sergey - II" sia vera, quindi entrambe le affermazioni della prima persona sono errate e ciò contraddice le condizioni del problema. Supponiamo che l'affermazione "Jura - II" sia vera, allora la prima affermazione della prima persona è falsa e la seconda è vera. E la prima affermazione della seconda persona è errata, ma la seconda è corretta.

Risposta: primo posto - Petya, secondo posto - Yura, terzo posto - Vitya, quarto posto Sergey.

2.6 Problemi risolti dalla fine.

C'è un tipo di problemi logici che vengono risolti dalla fine. Diamo un'occhiata a un esempio di risoluzione di tali problemi.

Compito 9. Vasya pensò a un numero, vi aggiunse 5, poi divise la somma per 3, moltiplicò per 4, sottrasse 6, divise per 7 e ottenne il numero 2. A quale numero pensò Vasya?

Soluzione: 2·7=14

14+6=20

20˸4=5

5·3=15

15-5=10

Risposta: Vasya ha pensato al numero 10.

Capitolo 3. Studiare la capacità di risolvere problemi logici.

Nella parte pratica del lavoro di ricerca ho selezionato problemi logici del tipo: problemi risolti dalla fine; chi è chi?; problemi di parole.

I compiti corrispondevano rispettivamente al livello di conoscenza del 5°, 6° e 7° anno. Gli studenti hanno risolto questi problemi e io ho analizzato i risultati (Fig. 1). Consideriamo più nel dettaglio i risultati ottenuti.

*Per la quinta elementare sono stati proposti i seguenti compiti:

Compito n. 1. Un problema risolto alla fine.

Ho pensato a un numero, l'ho moltiplicato per due, ho aggiunto tre e ho ottenuto 17. A quale numero ho pensato?

Compito n. 2. Problemi come "Chi è chi?"

Katya, Sonya e Lisa hanno il cognome Vasnetsova, Ermolaeva e Kuznetsova. Quale cognome ha ogni ragazza se Sonya, Liza ed Ermolaeva sono membri di un circolo matematico e Liza e Kuznetsova studiano musica?

Compito n.3. Compito di testo.

Alle Olimpiadi sportive scolastiche hanno preso parte 124 persone, 32 più ragazzi che ragazze. Quanti ragazzi e ragazze hanno partecipato alle Olimpiadi?

La maggior parte degli studenti di quinta elementare ha affrontato un problema del tipo: “risolvibile dalla fine”. Tali problemi si trovano nei libri di testo per le classi 5-6.Con il tipo di attività di testo, questo compito è più complesso, era necessario pensarci, solo 5 persone l'hanno affrontato.(Fig.2)

*Per la 6a elementare sono stati proposti i seguenti compiti:

Compito n. 1. Un problema risolto alla fine.

Ho pensato a un numero, ho sottratto 57, diviso per 2 e ho ottenuto 27. A quale numero ho pensato?

Compito n. 2. Problemi come "Chi è chi?"

Athos, Porthos, Aramis e D'Artagnan sono quattro giovani moschettieri di talento. Uno di loro combatte meglio con le spade, l'altro non ha eguali nel combattimento corpo a corpo, il terzo balla meglio ai balli, il quarto spara con le pistole senza perdere un colpo. Di loro si sa quanto segue:

Athos e Aramis osservarono il ballo del loro amico, un eccellente ballerino.

Porthos e il miglior tiratore ieri hanno assistito con ammirazione al combattimento corpo a corpo.

L'assassino vuole invitare Athos a fargli visita.

Porthos era molto grosso, quindi ballare non era il suo elemento.

Chi fa cosa?

Compito n.3. Compito di testo. Su uno scaffale ci sono 5 volte più libri che sul secondo. Dopo che 12 libri furono spostati dal primo al secondo scaffale, sugli scaffali rimase un numero uguale di libri. Quanti libri c'erano originariamente su ogni scaffale?

Tra i 18 studenti del sesto anno, 1 persona ha completato tutti i compiti. Tutti gli studenti della sesta elementare hanno affrontato un problema del tipo: "risolvibile dalla fine". Con il compito n. 2, come "Chi è chi?" Lo hanno fatto 4 persone. Solo una persona ha completato l'attività di testo(Fig. 3).

*Per la 7a elementare sono stati proposti i seguenti compiti:

Compito n. 1. Un problema risolto alla fine.

Ho pensato a un numero, ci ho aggiunto 5, poi ho diviso la somma per 3, moltiplicato per 4, sottratto 6, diviso per 7 e ho ottenuto il numero 2. A quale numero ho pensato?

Compito n. 2. Problemi come "Chi è chi?"

Vanya, Petya, Sasha e Kolya hanno cognomi che iniziano con le lettere V, P, S e K. È noto che 1) Vanya e S. sono studenti eccellenti; 2) Petya e V. sono studenti C; 3) Più alto di P.; 4) Kolya è più basso di P.; 5) Sasha e Petya hanno la stessa altezza. Con quale lettera inizia il cognome di tutti?

Compito n.3. Metodo di ragionamento.

Una squadra è arrivata per riparare la scuola, che comprendeva 2,5 volte più pittori che falegnami. Ben presto il caposquadra incluse altri 4 pittori nella squadra e trasferì due falegnami in un altro cantiere. Di conseguenza, nella squadra c'erano 4 volte più pittori che falegnami. Quanti pittori e quanti falegnami c'erano inizialmente nella squadra?

Tra i 20 studenti del 7° anno, 1 persona ha completato tutti i compiti.Tredici studenti hanno completato il problema del tipo “risolto dalla fine”. CONUno studente ha completato l'attività testuale (Fig. 4).

Conclusione

Durante il lavoro di ricerca sullo studio dei metodi per risolvere problemi logici. Considero raggiunti gli scopi e gli obiettivi che mi sono prefissato. Nel primo capitolo ho conosciuto il concetto di logica come scienza, le fasi principali del suo sviluppo e gli scienziati che ne sono i fondatori. Nel secondo capitolo ho studiato vari metodi per risolvere problemi logici e li ho analizzati utilizzando esempi specifici. Ho considerato i seguenti metodi: mmetodo di ragionamento, metodo delle tabelle, metodo del grafico, metodo del diagramma a blocchi, metodo del cerchio di Eulero, problemi di verità, metodo per risolvere un problema dalla fine.Nel terzo capitolo ho condotto uno studio pratico tra gli studenti delle classi 5-7, testando la loro capacità di risolvere problemi logici. La mia ricerca ha dimostrato quanto segue. I problemi completati dalla maggior parte degli studenti erano problemi risolti dalla fine. Con il compito "Chi è chi?" (metodo tabellare) metà degli studenti lo hanno fatto. Solo un numero esiguo di persone ha risolto il problema delle parole (metodo del ragionamento). Credo che la mia ipotesi sia stata parzialmente confermata, poiché la metà degli studenti ha avuto difficoltà a risolvere problemi logici.

I compiti logici aiutano a sviluppare il pensiero logico e fantasioso.Ogni bambino normale ha un desiderio di conoscenza, un desiderio di mettersi alla prova. Molto spesso, le capacità degli scolari rimangono nascoste, non hanno fiducia nelle proprie capacità e sono indifferenti alla matematica.Per tali studenti, propongo l'utilizzo di compiti logici. Questi compiti possono essere presi in considerazione nelle classi di club e opzionali. Devono essere accessibili, risvegliare l'intelligenza, catturare la loro attenzione, sorprendere, risvegliare l'immaginazione attiva e le decisioni indipendenti. Credo anche che la logica ci aiuti a far fronte a qualsiasi difficoltà della nostra vita e che tutto ciò che facciamo dovrebbe essere compreso e strutturato logicamente. Incontriamo logica e problemi logici non solo a scuola nelle lezioni di matematica, ma anche in altre materie.

Letteratura

Vilenkin N.Ya. Matematica 5a elementare.-Mnemosyne, M: 2015. 45 pagg.

Vilenkin N.Ya. Matematica 5a elementare.-Mnemosyne, M: 2015. 211 pagg.

Orlova E. Metodi risolutivi problemi logici e problemi numerici //

Matematica. -1999. N. 26. - pp. 27-29.

Tarski A. Introduzione alla logica e alla metodologia delle scienze deduttive - Mosca: 1948.

Risorse Internet:

http://wiki. Insegno.

Riso. 3 Analisi del lavoro di 6a elementare.

Riso. 4 Analisi del lavoro di 7a elementare

Istituzione comunale di bilancio educativo -

Scuola secondaria n. 51

Orenburg.

Progetto su:

insegnante di matematica

Egorcheva Vittoria Andreevna

2017

Ipotesi : Se la teoria dei grafi viene avvicinata alla pratica, si possono ottenere i risultati più vantaggiosi.

Bersaglio: Acquisisci familiarità con il concetto di grafici e impara come applicarli nella risoluzione di vari problemi.

Compiti:

1) Ampliare la conoscenza sui metodi di costruzione dei grafici.

2) Individuare tipologie di problemi la cui soluzione richiede l'uso della teoria dei grafi.

3) Esplora l'uso dei grafici in matematica.

"Eulero calcolò, senza alcuno sforzo visibile, come una persona respira o come un'aquila si libra sopra la terra."

Domenico Arago.

IO. Introduzione. P.

II . Parte principale.

1. Il concetto di grafico. Problema sui ponti di Königsberg. P.

2. Proprietà dei grafici. P.

3. Problemi nell'uso della teoria dei grafi. P.

Sh. Conclusione.

Il significato dei grafici. P.

IV. Bibliografia. P.

IO . INTRODUZIONE

La teoria dei grafi è una scienza relativamente giovane. “Grafici” deriva dalla parola greca “grapho”, che significa “io scrivo”. La stessa radice è nelle parole “grafico”, “biografia”.

Nel mio lavoro, guardo come la teoria dei grafi viene utilizzata in vari ambiti della vita delle persone. Ogni insegnante di matematica e quasi ogni studente sa quanto sia difficile risolvere problemi geometrici, così come problemi di algebra. Dopo aver esplorato la possibilità di utilizzare la teoria dei grafi in un corso di matematica scolastica, sono giunto alla conclusione che questa teoria semplifica notevolmente la comprensione e la risoluzione dei problemi.

II . PARTE PRINCIPALE.

1. Il concetto di grafico.

Il primo lavoro sulla teoria dei grafi appartiene a Leonhard Euler. Apparve nel 1736 nelle pubblicazioni dell'Accademia delle scienze di San Pietroburgo e iniziò con una considerazione del problema dei ponti di Königsberg.

Probabilmente sai che esiste una città come Kaliningrad; una volta si chiamava Koenigsberg. Il fiume Pregolya scorre attraverso la città. Si divide in due rami e fa il giro dell'isola. Nel XVII secolo in città c'erano sette ponti, disposti come mostrato nella foto.

Si racconta che un giorno un abitante della città chiese ad un suo amico se poteva attraversare tutti i ponti in modo da visitarli una sola volta e tornare al luogo da cui aveva avuto inizio la passeggiata. Molti cittadini si interessarono a questo problema, ma nessuno riuscì a trovare una soluzione. Questo problema ha attirato l'attenzione di scienziati di molti paesi. Il famoso matematico Leonhard Euler riuscì a risolvere il problema. Leonhard Euler, originario di Basilea, nacque il 15 aprile 1707. I risultati scientifici di Eulero sono enormi. Ha influenzato lo sviluppo di quasi tutti i rami della matematica e della meccanica, sia nel campo della ricerca fondamentale che nelle loro applicazioni. Leonhard Euler non solo risolse questo problema specifico, ma elaborò anche un metodo generale per risolverli. Eulero fece quanto segue: “compresse” la terra in punti e “allungò” i ponti in linee. Il risultato è la figura mostrata in figura.

Viene chiamata una tale figura, composta da punti e linee che collegano questi punticontare. Punti A, B, C, D sono chiamati vertici del grafico e le linee che collegano i vertici sono chiamate bordi del grafico. In un disegno di vertici B, C, D Escono 3 costole, e dalla parte superiore UN - 5 costole. Si chiamano vertici dai quali emergono un numero dispari di spigolivertici dispari, e i vertici da cui emergono un numero pari di spigoli sonoAnche.

2. Proprietà del grafico.

Risolvendo il problema dei ponti di Königsberg, Eulero stabilì, in particolare, le proprietà del grafo:

1. Se tutti i vertici del grafico sono pari, puoi disegnare un grafico con un tratto (cioè senza sollevare la matita dal foglio e senza disegnare due volte lungo la stessa linea). In questo caso il movimento può iniziare da qualsiasi vertice e terminare allo stesso vertice.

2. Un grafico con due vertici dispari può anche essere disegnato con un tratto. Il movimento deve iniziare da qualsiasi vertice dispari e terminare in un altro vertice dispari.

3. Un grafico con più di due vertici dispari non può essere disegnato con un solo tratto.

4.Il numero di vertici dispari in un grafico è sempre pari.

5. Se un grafico ha vertici dispari, il numero minimo di tratti che possono essere utilizzati per disegnare il grafico sarà pari alla metà del numero di vertici dispari di questo grafico.

Ad esempio, se una figura ha quattro numeri dispari, può essere disegnata con almeno due tratti.

Nel problema dei sette ponti di Königsberg tutti e quattro i vertici del grafo corrispondente sono dispari, cioè Non puoi attraversare tutti i ponti una volta e terminare il viaggio da dove è iniziato.

3. Risoluzione di problemi utilizzando i grafici.

1. Compiti sul disegno di figure con un colpo.

Il tentativo di disegnare ciascuna delle seguenti forme con un tratto di penna produrrà risultati diversi.

Se nella figura non sono presenti punti dispari, è sempre possibile disegnarla con un tratto di penna, indipendentemente da dove si inizia a disegnare. Queste sono le figure 1 e 5.

Se una figura ha solo una coppia di punti dispari, allora tale figura può essere disegnata con un tratto, iniziando a disegnare da uno dei punti dispari (non importa quale). È facile capire che il disegno dovrebbe terminare al secondo punto dispari. Queste sono le figure 2, 3, 6. Nella figura 6, ad esempio, il disegno deve iniziare o dal punto A o dal punto B.

Se una figura ha più di una coppia di punti dispari, non può essere disegnata con un solo tratto. Queste sono le figure 4 e 7, contenenti due coppie di punti dispari. Quanto detto è sufficiente per riconoscere con precisione quali figure non possono essere disegnate in un colpo solo e quali invece si possono disegnare, nonché da quale punto deve iniziare il disegno.

Propongo di disegnare le seguenti figure in un colpo solo.

2. Risoluzione di problemi logici.

COMPITO N. 1.

Ci sono 6 partecipanti al campionato di classe di ping pong: Andrey, Boris, Victor, Galina, Dmitry ed Elena. Il campionato si svolge secondo il sistema round robin: ogni partecipante gioca contro gli altri una volta. Ad oggi alcune partite sono già state giocate: Andrey ha giocato con Boris, Galina, Elena; Boris - con Andrey, Galina; Victor - con Galina, Dmitry, Elena; Galina - con Andrey, Victor e Boris. Quante partite sono state giocate finora e quante ne restano?

SOLUZIONE:

Costruiamo un grafico come mostrato in figura.

7 partite giocate.

In questa figura, il grafico ha 8 spigoli, quindi ci sono 8 giochi rimasti da giocare.

COMPITO N.2

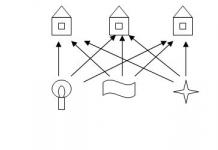
Nel cortile, circondato da un alto recinto, ci sono tre case: rossa, gialla e blu. La recinzione ha tre cancelli: rosso, giallo e blu. Dalla casa rossa traccia un percorso verso il cancello rosso, dalla casa gialla al cancello giallo, dalla casa blu a quella blu in modo che questi percorsi non si intersechino.

SOLUZIONE:

La soluzione al problema è mostrata in figura.

3. Risoluzione di problemi con le parole.

Per risolvere i problemi utilizzando il metodo del grafico, è necessario conoscere il seguente algoritmo:

1.Di quale processo stiamo parlando nel problema?2.Quali quantità caratterizzano questo processo?3.Qual è la relazione tra queste quantità?4.Quanti processi diversi sono descritti nel problema?5.Esiste una connessione tra gli elementi?

Rispondendo a queste domande, analizziamo la condizione del problema e lo scriviamo schematicamente.

Per esempio . L'autobus ha viaggiato per 2 ore ad una velocità di 45 km/h e per 3 ore ad una velocità di 60 km/h. Quanto ha percorso l'autobus in queste 5 ore?

S
¹=90 km V ¹=45 km/h t ¹=2h

S=VT

S²=180 km V²=60 km/h t²=3 h

S ¹ + S ² = 90 + 180

Soluzione:

1)45x 2 = 90 (km) - l'autobus ha viaggiato in 2 ore.

2)60x 3 = 180 (km) - l'autobus ha percorso in 3 ore.

3)90 + 180 = 270 (km) - l'autobus ha percorso in 5 ore.

Risposta: 270 km.

III . CONCLUSIONE.

Come risultato del lavoro sul progetto, ho appreso che Leonhard Euler è stato il fondatore della teoria dei grafi e ha risolto i problemi utilizzando la teoria dei grafi. Ho concluso da solo che la teoria dei grafi è utilizzata in varie aree della matematica moderna e nelle sue numerose applicazioni. Non c’è dubbio sull’utilità di introdurre noi studenti ai concetti base della teoria dei grafi. Risolvere molti problemi matematici diventa più semplice se puoi utilizzare i grafici. Presentazione dei dati V la forma di un grafico dà loro chiarezza. Molte dimostrazioni vengono inoltre semplificate e diventano più convincenti se si utilizzano i grafici. Ciò vale soprattutto per aree della matematica come la logica matematica e la combinatoria.

Pertanto, lo studio di questo argomento ha un grande significato educativo generale, culturale generale e matematico generale. Nella vita di tutti i giorni vengono sempre più utilizzate illustrazioni grafiche, rappresentazioni geometriche e altre tecniche e metodi visivi. A questo scopo è utile introdurre lo studio di elementi di teoria dei grafi nelle scuole primarie e secondarie, almeno nelle attività extrascolastiche, poiché questo argomento non è compreso nel curricolo di matematica.

V . BIBLIOGRAFIA:

2008

Revisione.

Il progetto sul tema "Grafici intorno a noi" è stato completato da Nikita Zaytsev, uno studente della classe 7 "A" presso l'istituto scolastico municipale n. 3, Krasny Kut.

Una caratteristica distintiva del lavoro di Nikita Zaitsev è la sua rilevanza, l’orientamento pratico, la profondità della trattazione dell’argomento e la possibilità di utilizzarlo in futuro.

Il lavoro è creativo, sotto forma di progetto informativo. Lo studente ha scelto questo argomento per mostrare il rapporto tra la teoria dei grafi e la pratica utilizzando l'esempio di un percorso di uno scuolabus, per mostrare che la teoria dei grafi è utilizzata in varie aree della matematica moderna e nelle sue numerose applicazioni, soprattutto in economia, logica matematica e combinatoria . Ha dimostrato che la risoluzione dei problemi è notevolmente semplificata se è possibile utilizzare i grafici; la presentazione dei dati sotto forma di grafico li rende chiari; anche molte dimostrazioni vengono semplificate e diventano convincenti.

Il lavoro affronta temi quali:

1. Il concetto di grafico. Problema sui ponti di Königsberg.

2. Proprietà dei grafici.

3. Problemi nell'uso della teoria dei grafi.

4. Il significato dei grafici.

5. Opzione percorso scuolabus.

Durante l'esecuzione del suo lavoro, N. Zaitsev ha utilizzato:

1. Alkhova Z.N., Makeeva A.V. "Lavoro extracurriculare in matematica."

2. Rivista “La matematica a scuola”. Appendice “Primo settembre” n. 13

2008

3. Ya.I.Perelman "Compiti ed esperimenti divertenti." - Mosca: Istruzione, 2000.

Il lavoro è stato svolto con competenza, il materiale soddisfa i requisiti di questo argomento, i disegni corrispondenti sono allegati.

Metodi per risolvere problemi logici

Trosheva Natalya, 7a elementare

1 . La logica è necessaria a qualsiasi specialista, sia esso un matematico, un medico o un biologo. La logica è uno strumento necessario che ti libera da memorizzazioni inutili e non necessarie, aiutandoti a trovare nella massa di informazioni ciò che è prezioso di cui una persona ha bisogno. Senza logica, questo è un lavoro cieco.

Durante tutti gli anni di studio a scuola, risolviamo molti problemi diversi, compresi quelli logici: problemi divertenti, enigmi, anagrammi, rebus, ecc. Per risolvere con successo problemi di questo tipo, è necessario essere in grado di identificare le loro caratteristiche comuni, notare modelli, avanzare ipotesi, testarle, costruire catene di ragionamento e trarre conclusioni. I problemi logici differiscono da quelli ordinari in quanto non richiedono calcoli, ma vengono risolti utilizzando il ragionamento. Possiamo dire che un compito logico è un'informazione speciale che non solo deve essere elaborata in conformità con una determinata condizione, ma vuoi anche farlo. Un posto speciale in matematica è occupato dai problemi, la cui soluzione sviluppa il pensiero logico, che contribuisce allo studio di successo della materia. Questi problemi sono divertenti e non richiedono molte conoscenze matematiche, quindi attirano anche quegli studenti a cui non piace molto la matematica.

2. Il mio lavoro didattico e di ricerca è di natura teorica.

Scopo il lavoro consiste nel familiarizzare con diversi tipi di problemi logici, algoritmi e metodi per risolverli.

Per raggiungere questo obiettivo è necessario risolvere quanto segue compiti:

1. studiare la letteratura per acquisire familiarità con diversi tipi di problemi logici e metodi per risolverli,

2. applicare questi metodi per risolvere vari tipi di problemi logici, 3. selezionare problemi logici che possono essere risolti con un determinato metodo.

Un oggetto ricerca – problemi logici nel programma di matematica in una scuola educativa.

Articolo ricerca – una varietà di metodi per risolvere problemi logici.

Metodi ricerca:

analisi e sintesi, confronto.

3. La soluzione di molti problemi logici implica la considerazione di più insiemi finiti con lo stesso numero di elementi, tra i quali è necessario stabilire una corrispondenza. Quando si risolvono tali problemi è conveniente da usare algoritmo di soluzione

Quando risolviamo problemi logici usiamo quanto segue algoritmo:

1) Determinazione del contenuto del testo (selezione di oggetti o soggetti).

2) Compilazione di informazioni complete sull'evento.

3) Formazione di un compito escludendo parte dell'informazione o distorcendola.

4) Formulazione arbitraria del problema. Se necessario (mancanza di informazioni, distorsione, ecc.), viene introdotta un'ulteriore condizione logica.

5) Verificare la possibilità di una soluzione utilizzando il ragionamento. Ricevere un'unica risposta coerente significa che la condizione è corretta. In caso contrario, è necessario fare riferimento alla clausola aggiuntiva 6.

6) La condizione compilata è priva di informazioni o le informazioni disponibili sono distorte in modo incoerente. Modifichiamo o integriamo la condizione del problema, dopodiché dobbiamo passare al passaggio 5.

4. Per lo sviluppo della memoria e la generalizzazione delle conoscenze acquisite sono interessanti i test logici. Per risolvere i test di matematica, oltre alle conoscenze della matematica scolastica, è necessaria la capacità di osservare, confrontare, generalizzare, trarre analogie, trarre conclusioni e giustificarle. Fondamentalmente, i test sono compiti creativi che promuovono lo sviluppo del pensiero logico.

I test logici si dividono in tre gruppi principali:

verbale

simbolico-grafico

combinato

Il mondo dei test logici simbolico-grafici è molto vario e ricco. I compiti sono un modo efficace per collegare il materiale algebrico con la rappresentazione di figure matematiche.

Inserisci la forma richiesta:

? 100

Esempio. Inserisci la parola mancante

argomento matematica 3≤x≤6

decimetro 5≤x≤8 ?

La logica aiuta ad assimilare la conoscenza consapevolmente, con comprensione, cioè. non formale; crea la possibilità di una migliore comprensione reciproca. La logica è l'arte del ragionamento, la capacità di trarre conclusioni corrette. Questo non è sempre facile, perché molto spesso le informazioni necessarie sono “mascherate”, presentate implicitamente, e bisogna poterle estrarre.

5. I problemi di logica del testo possono essere suddivisi nei seguenti tipi:

tutte le affermazioni sono vere;

non tutte le affermazioni sono vere;

problemi relativi a coloro che dicono la verità e ai bugiardi.

È consigliabile esercitarsi a risolvere ogni tipo di problema gradualmente, passo dopo passo.

6. Diamo un'occhiata ai metodi di base per risolvere i problemi e all'applicazione di alcuni metodi a problemi specifici.

Metodo di ragionamento

Nel metodo di ragionamento durante la risoluzione, quanto segue aiuta: diagrammi, disegni, brevi note, la capacità di selezionare le informazioni, la capacità di utilizzare la regola di enumerazione.

Esempio.

Lena, Olya, Tanya hanno preso parte alla gara dei 100 m, Lena ha corso 2 secondi prima di Olya, Olya ha corso 1 secondo dopo Tanya. Chi è arrivato correndo prima: Tanya o Lena e entro quanti secondi?

Soluzione.

Facciamo uno schema:

Lena __________

Olja __________ __ __

Tanja __________ __

Risposta. In precedenza, Lena è arrivata al 1°.

Metodo per descrivere gli oggetti e le loro forme

In base alla descrizione puoi immaginare un oggetto, un luogo o un evento che non hai mai visto. Sulla base dei segni (segni) del criminale, viene realizzato il suo presunto ritratto: un identikit.

Sulla base dei segni (sintomi) della malattia, il medico formula una diagnosi, ad es. riconosce la malattia.

Risolvere molti enigmi, sciarade e risolvere cruciverba si basa sul riconoscimento di un oggetto tramite la descrizione.

Metodo per individuare i problemi correlati

Se il problema è difficile, è necessario provare a trovare e risolvere un problema "correlato" più semplice. Ciò fornisce la chiave per risolvere il problema originale.

Il metodo di "vagliare i compiti" (o "possiamo supporre che ...")

Puoi risolvere il problema secondo necessità, oppure puoi prima trasformarlo in una forma conveniente per la soluzione: riformulare la condizione in un linguaggio più conveniente (ad esempio, nel linguaggio di un disegno), scartare casi semplici, ridurre il caso generale a uno particolare.

Metodo pari-dispari

Molti problemi possono essere facilmente risolti se si nota che una certa quantità ha una certa parità. Ne consegue che sono impossibili situazioni in cui una data quantità ha una parità diversa. A volte questa quantità ha bisogno di essere “costruita”, ad esempio per considerare la parità di una somma o di un prodotto, oppure per dividere gli oggetti in coppie. Notare l'alternanza degli stati, dipingere gli oggetti in due colori, ecc.

Esempi.

La cavalletta saltò lungo una linea retta e tornò al punto di partenza (lunghezza del salto 1 m). Dimostrare che ha effettuato un numero pari di salti.

Soluzione. Perché la cavalletta è tornata al punto di partenza. Il numero di salti a destra è uguale al numero di salti a sinistra, quindi il numero totale di salti è pari.

Metodo inverso

Se nel problema è specificata una determinata operazione ed è reversibile, è possibile effettuare un passaggio "inverso" dal risultato finale ai dati originali. (Ad esempio, devi portare un armadio fuori dalla stanza. Passerà attraverso la porta? Lo farà perché è stato portato dentro attraverso la porta). L'analisi end-to-end viene utilizzata per trovare situazioni vincenti e perdenti.

Metodo della tabella

Questo metodo consiste nel compilare una tabella e nell'inserirvi i dati in base alle condizioni del problema.

Metodo grafico

La parola “grafico” è apparsa nella letteratura matematica abbastanza recentemente. Il concetto di grafico viene utilizzato non solo in matematica, ma anche nella tecnologia e persino nella vita di tutti i giorni con nomi diversi: diagramma, diagramma.

I grafici sono particolarmente utili quando si risolvono problemi logici. Presentando gli oggetti studiati in forma visiva, i “grafici” aiutano a conservare in memoria numerosi fatti contenuti nella formulazione del problema e a stabilire connessioni tra loro.

Contareè un qualsiasi insieme di punti, alcuni dei quali sono collegati da linee o frecce. Si chiamano i punti che rappresentano gli elementi di un insieme picchi grafico che collega i loro segmenti - costolette grafico. I punti di intersezione dei bordi di un grafico non sono i suoi vertici. Per evitare confusione, i vertici di un grafico sono spesso rappresentati non come punti, ma come piccoli cerchi. A volte è più conveniente rappresentare i bordi non come segmenti diritti, ma come archi.

Metodo del cerchio di Eulero

Questo metodo fornisce un'idea ancora più visiva di un possibile modo per rappresentare condizioni, dipendenze e relazioni nei problemi logici.

Uno dei più grandi matematici, l'accademico di San Pietroburgo Leonard Euler, scrisse più di 850 articoli scientifici durante la sua lunga vita. Questi cerchi sono apparsi in uno di essi. Eulero scriveva allora che “sono molto adatti per facilitare le nostre riflessioni”. Insieme ai cerchi, in questi problemi vengono utilizzati rettangoli e altre forme.

Esempio.

1. Alcuni residenti della città parlano solo russo, altri solo uzbeko e altri ancora entrambe le lingue. L'85% parla uzbeko, il 75% russo. Qual è la percentuale dei residenti che parlano entrambe le lingue?

Soluzione. Facciamo un diagramma -

Nel cerchio sotto la lettera "U" denotiamo residenti che parlano uzbeko, sotto la lettera "R" - in russo. Nella parte generale dei cerchi designiamo i residenti che parlano entrambe le lingue. Ora, da tutti i residenti (100%), sottraiamo il cerchio “U” (85%) e otteniamo i residenti che parlano solo russo (15%). E ora sottraiamo questo 15% a tutti coloro che parlano russo (75%). Prendiamo i parlanti di entrambe le lingue (60%).

Metodo combinato

Un metodo in cui un problema può essere risolto in diversi modi.

Il materiale proposto "Metodi per risolvere problemi logici" può essere utilizzato sia nelle lezioni di matematica che in attività extrascolastiche per gli studenti delle classi 5-9, insegnanti per preparare gli studenti a risolvere i compiti delle Olimpiadi, competizioni intellettuali "Maratona della conoscenza", competizione regionale “Canguro”.

Avendo conosciuto diversi tipi di problemi logici e metodi per risolverli, credo di poter applicare le conoscenze acquisite nelle mie attività educative, scegliere autonomamente l'uno o l'altro metodo di soluzione per un problema specifico e applicare i metodi appresi per risolvere un problema in una situazione reale.

Istituzione educativa di bilancio comunale

"Liceo multidisciplinare" dell'insediamento urbano "Villaggio operaio Chegdomyn" Verkhnebureinsky Municipal

regione del territorio di Khabarovsk.

Lavoro di ricerca astratto in matematica:

Argomento: "Metodo di induzione matematica"

Completato da: Svetlana Antonova

studente di 11 classe "B".

Responsabile: Terentyeva O. A.

insegnante di matematica

villaggio Chegdomyn

1.Introduzione 3

2. Storia

metodo di induzione matematica 4-5

3. Principali risultati dello studio 6-14

4. Compiti previsti per l'Esame di Stato Unificato 15-18

5.Conclusione 19 6.Riferimenti 20

Introduzione:

All'inizio della 10a elementare abbiamo iniziato a studiare il metodo dell'induzione matematica, anche allora ero molto interessato a questo argomento, ma solo per studio. Quando abbiamo iniziato una preparazione intensiva per superare l'esame di stato unificato in matematica, i compiti su questo argomento sono stati molto facili per me e mi sono interessato alle possibilità di questo metodo nella risoluzione di compiti più complessi. Insieme all'insegnante, abbiamo deciso di studiare questo metodo e le sue capacità in modo più dettagliato e approfondito quando lavoriamo a un progetto su questo argomento.

Lo scopo del mio lavoro:

Familiarizza con il metodo di induzione matematica, sistematizza la conoscenza su questo argomento e applica questo metodo quando risolvi problemi matematici e dimostri teoremi.

Obiettivi lavorativi:

1. Aggiornare il significato pratico delle conoscenze matematiche.

2.Sviluppo di idee morali sulla natura della matematica, l'essenza e l'origine dell'astrazione matematica.

3. Padroneggiare diversi metodi e tecniche di lavoro.

4. Generalizzazione e sistematizzazione delle conoscenze su questo argomento.

5. Applicazione delle conoscenze acquisite durante la risoluzione dei compiti dell'Esame di Stato unificato.

Problema:

Mostrare il significato pratico del metodo di induzione matematica.

Dalla storia dell'emergere del metodo di induzione matematica:

La straordinaria espansione della materia matematica nel XIX secolo attirò maggiore attenzione alle questioni relative alla sua “giustificazione”, vale a dire una revisione critica delle sue disposizioni iniziali (assiomi), la costruzione di un rigoroso sistema di definizioni e dimostrazioni, nonché un esame critico degli esempi logici utilizzati in queste dimostrazioni.

Solo verso la fine del XIX secolo emerse uno standard di requisiti di rigore logico, che rimangono ancora oggi dominanti nel lavoro pratico dei matematici sullo sviluppo delle singole teorie matematiche.

La logica matematica moderna ha dato una risposta definitiva a questa domanda: nessuna singola teoria deduttiva può esaurire la varietà di problemi della teoria dei numeri.

La parola induzione in russo significa guida e induttiva sono conclusioni tratte sulla base di osservazioni, esperimenti, ad es. ottenuto per inferenza dal particolare al generale.

La base di qualsiasi ricerca matematica sono i metodi deduttivi e induttivi. Il metodo di ragionamento deduttivo è il ragionamento dal generale allo specifico, cioè. ragionamento, il cui punto di partenza è il risultato generale e il punto finale è il risultato particolare. L'induzione viene utilizzata quando si passa da risultati particolari a quelli generali, ad es. è l'opposto del metodo deduttivo.

Il metodo dell'induzione matematica può essere paragonato al progresso. Iniziamo dal più basso e, come risultato del pensiero logico, arriviamo al più alto. L'uomo ha sempre cercato il progresso, la capacità di sviluppare i suoi pensieri in modo logico, il che significa che la natura stessa lo ha destinato a pensare induttivamente.

Il ruolo delle conclusioni induttive nelle scienze sperimentali è molto grande. Essi forniscono le disposizioni dalle quali si traggono poi ulteriori conclusioni mediante detrazione. E sebbene la meccanica teorica si basi sulle tre leggi del moto di Newton, queste leggi stesse sono il risultato di una profonda riflessione attraverso dati sperimentali, in particolare le leggi del moto planetario di Keplero, che egli derivò dall'elaborazione di molti anni di osservazioni da parte dell'astronomo danese Tycho Brahe. L'osservazione e l'induzione si rivelano utili in futuro per chiarire le ipotesi fatte. Dopo gli esperimenti di Michelson sulla misurazione della velocità della luce in un mezzo in movimento, si è rivelato necessario chiarire le leggi della fisica e creare la teoria della relatività.

In matematica, il ruolo dell'induzione è in gran parte quello di essere alla base dell'assiomatica scelta. Dopo che la pratica a lungo termine ha dimostrato che un percorso rettilineo è sempre più breve di uno curvo o spezzato, è stato naturale formulare un assioma: per tre punti qualsiasi A, B e C, la disuguaglianza

Il concetto di "seguire ...", che è la base dell'aritmetica, è emerso anche dalle osservazioni della formazione di soldati, navi e altri insiemi ordinati.

Non si deve però pensare che questo esaurisca il ruolo dell’induzione in matematica. Naturalmente, non dovremmo verificare sperimentalmente i teoremi dedotti logicamente dagli assiomi: se durante la derivazione non sono stati commessi errori logici, allora essi sono veri nella misura in cui sono veri gli assiomi che abbiamo accettato. Ma da questo sistema di assiomi si possono dedurre molte affermazioni. E la selezione delle affermazioni che necessitano di essere dimostrate è suggerita ancora una volta dall'induzione. È questo che permette di separare i teoremi utili da quelli inutili, indica quali teoremi possono rivelarsi veri e aiuta anche a delineare il percorso della dimostrazione.

In matematica, il metodo induttivo è stato a lungo utilizzato, basato sul fatto che l'una o l'altra affermazione generale viene fatta considerando solo pochi casi speciali. La storia, ad esempio, ha conservato la seguente affermazione di Eulero: “Non ho altri argomenti a sostegno della dimostrazione, eccetto una lunga induzione, che ho portato così lontano che non posso in alcun modo dubitare della legge che regola la formazione di questi membri. E sembra impossibile che una legge che si è rivelata valida, ad esempio, per 20 membri, non possa essere osservata per i successivi.

Credendo nell'infallibilità dell'induzione, gli scienziati a volte commettevano gravi errori.

Verso la metà del XVII secolo in matematica si erano accumulate molte conclusioni errate. Cominciò ad essere forte la necessità di un metodo scientificamente fondato che consentisse di trarre conclusioni generali dall'esame di numerosi casi specifici. E un tale metodo è stato sviluppato. Il merito principale di ciò va ai matematici francesi Pascal (1623 - 1662) e Cartesio, nonché al matematico svizzero Jacob Bernoulli (1654-1705).

Principali risultati della fase di ricerca.

Nel processo di lavoro, ho scoperto che tutte le affermazioni possono essere suddivise in generali e specifiche. Un esempio di affermazione generale è, ad esempio, l'affermazione: "In ogni triangolo, la somma di due lati è maggiore del terzo lato". Ad esempio l'affermazione: “Il numero 136 è divisibile per 2” è particolare.

Viene chiamata la transizione dalle affermazioni generali a quelle specifiche nonno zione. In matematica utilizziamo il metodo deduttivo, ad esempio, in ragionamenti di questo tipo: questa figura è un rettangolo; Ogni rettangolo ha le diagonali uguali, quindi questo rettangolo ha le diagonali uguali.

Ma insieme a questo, in matematica è spesso necessario passare da affermazioni particolari a affermazioni generali, ad es. utilizzare un metodo opposto a quello deduttivo, che si chiama per induzione .

Induttivo l'approccio di solito inizia con l'analisi e il confronto di dati osservativi o sperimentali. La ripetizione ripetuta di un fatto porta alla generalizzazione induttiva. Il risultato ottenuto per induzione, in generale, non è logicamente giustificato né dimostrato. Ci sono molti casi in cui le affermazioni ottenute per induzione erano errate. Cioè, l'induzione può portare a conclusioni sia corrette che errate.

Consideriamo esempio. Sostituzione in un trinomio quadratico P(x)=x 2 +x+41 invece di X numeri naturali 1,2,3,4,5, troviamo: P(1)= 43; P(2)=47; P(3)= 53; P(4)= 61; P(5)= 71. Tutti i valori di questo trinomio sono numeri primi. Sostituendo invece X numeri 0, -1, -2, -3, -4, otteniamo: P(0)=41; P(-1)=41; P(-2)=43; P(-3)=47; Р(-4) =53. I valori di questo trinomio per i valori specificati della variabile X sono anche numeri primi. Sorge un'ipotesi che il valore del trinomio P(x)è un numero primo per qualsiasi valore intero X. Ma espresso l'ipotesi è sbagliata, poiché, ad esempio, P(41)= 41 2 +41+41=41∙43.

Poiché con questo metodo la conclusione viene tratta dopo aver analizzato diversi esempi che non coprono tutti i casi possibili, questo metodo viene chiamato induzione incompleta o imperfetta.

Il metodo dell'induzione incompleta, come vediamo, non porta a conclusioni completamente affidabili, ma è utile in questo ci permette di formulare un’ipotesi, che può poi essere dimostrato con precisi ragionamenti matematici o confutato. In altre parole, l’induzione incompleta in matematica non è considerata un metodo legittimo di dimostrazione rigorosa, ma lo è potentemetodo euristico per scoprire nuove verità.

Se la conclusione viene tratta sulla base dell'analisi di tutti i casi, viene chiamato questo metodo di ragionamento induzione completa.

Qui esempio ragionamento simile. Sia necessario stabilire che ogni numero naturale pari P entro 10 P Quindi prendiamo tutti questi numeri e scriviamo le espansioni corrispondenti: 10=7+3; 12=7+5; 14=7+7; 16=11+5; 18=13+5; 20=13+7 . Queste sei uguaglianze mostrano che ciascuno dei numeri che ci interessano è infatti rappresentato come la somma di due termini semplici.

Lasciamo che qualche affermazione sia vera in diversi casi particolari. La considerazione di tutti gli altri casi è del tutto impossibile o richiede un gran numero di calcoli. Come fai a sapere se questa affermazione è vera? Questa domanda a volte può essere risolta applicando uno speciale metodo di ragionamento chiamato metodo matematico induzione .Basato su questo metodo bugie principio induzione matematica .

Se l'ipotesi dipende dal numero naturaleN, VEROPerN=1 e dal fatto che è vero perN= K(DoveK-qualsiasi naturalenumero), ne consegue che è vero per il numero successivoN= K+1, allora l'ipotesi è vera per qualsiasinumero naturaleN.

Il metodo di induzione matematica è un metodo efficace per dimostrare ipotesi (affermazioni), basato sull'uso del principio di induzione matematica, quindi porta solo a conclusioni corrette.

Utilizzando il metodo dell'induzione matematica Non tutti i problemi possono essere risolti, ma solo compiti, parametrizzato qualche variabile. Questa variabile è chiamata variabile di induzione.

Il metodo dell'induzione matematica è ampiamente utilizzato in aritmetica, algebra e teoria dei numeri.

Esempio 1. Trova l'importo Sn =

Innanzitutto, troviamo le somme di uno, due e tre termini. Abbiamo:

S 1 = ; S 2 = ; S 3 = .

In ciascuno di questi casi, si ottiene una frazione, il cui numeratore contiene il numero di termini e il denominatore contiene un numero maggiore di uno rispetto al numero di termini. Questo ti permette di esprimere ipotesi ( presupposto) che per qualsiasi naturale P Sp =.

Per verificare questa ipotesi, utilizzeremo il metodo dell'induzione matematica.

1) Quando P = 1 ipotesi è corretta, poiché S 1 = .

2) Supponiamo che l'ipotesi sia vera per P= k, cioè

S k = .

Dimostriamo che allora l'ipotesi deve essere vera anche per P = K+ 1, cioè

S K +1 = .

Veramente, S K +1 = S K

S K +1 =

Pertanto, sulla base del presupposto che l'ipotesi S P =

vero quando n = K, abbiamo dimostrato che è vero anche quando P = K + 1.

Quindi la formula S P = vero per qualsiasi naturale P.

Esempio 2. Dimostrarlo per qualsiasi numero naturale P e qualsiasi numero reale un -1 c'è una disuguaglianza chiamata Disuguaglianza di Bernoulli (dal nome del matematico svizzero del XVII secolo Jacob Bernoulli) : (1+ UN) P ≥ 1 + ca.

1) Se n=1, allora è ovvio che la disuguaglianza è vera: (1+a) 1 ≥ 1+a.

2) Supponiamo che la disuguaglianza sia vera per N= K: (1+ UN) K ≥ 1 + ok.

Moltiplica entrambi i membri dell'ultima disuguaglianza per un numero positivo 1+ un, di conseguenza otteniamo (1+ UN) K +1 ≥ 1+ ok+ UN+ UN 2 K.

Eliminando l'ultimo termine sul lato destro della disuguaglianza, riduciamo il lato destro di questa disuguaglianza, e quindi (1+ UN) K +1 ≥ UN(K+1).

Il risultato ottenuto mostra che la disuguaglianza vale anche per N= K+1.

Entrambe le parti della dimostrazione sono state effettuate utilizzando il metodo dell'induzione matematica, e quindi la disuguaglianza è valida per qualsiasi numero naturale P.

Si noti che l'intera soluzione è stata divisa in quattro fasi:

1.base(dimostriamo che l'affermazione da dimostrare è vera per alcuni casi speciali più semplici ( P = 1);

2.presupposto(supponiamo che l'affermazione sia stata dimostrata per la prima volta A casi; 3 .fare un passo(sotto questa ipotesi dimostriamo l'affermazione del caso P = A + 1 ); 4.uscita (a l'affermazione è vera per tutti i casi, cioè per tutti P) .

La seconda versione del metodo di induzione matematica.

Alcune affermazioni non sono vere per tutto il naturale P, ma solo per natura P, a partire da un certo numero R. Tali affermazioni possono talvolta essere dimostrate con un metodo leggermente diverso da quello sopra descritto, ma abbastanza simile ad esso. Consiste nel seguente.

L'affermazione è vera per tutti i valori naturalip ≥ p se: 1) è vero quando P=p (e non a P= 1, come detto sopra);

2) dalla validità di questa affermazione quando P= k, dove k ≥ р (e non k ≥ 1, come detto sopra), ne consegue che è vero anche quando P= k + 1.

Esempio 1. Dimostrare che l’uguaglianza è vera per tutti

Indichiamo il prodotto a sinistra dell'uguaglianza con , cioè

dobbiamo dimostrarlo.

Per n=1 la formula non è corretta (1- 1) = 1(errato).

1) Controlliamo che questa formula è vera per n = 2. , - vero.

2) Sia vera la formula per n = k, cioè

3) Proviamo che questa identità vale anche per n = k + 1, cioè

Secondo il principio di induzione matematica, l’uguaglianza è vera per qualsiasi numero naturale.

Esempio 2. Dimostrare che 22n + 1 per ogni numero naturale n3.

1) Per n = 3 la disuguaglianza è vera. 223+1.

2) Supponiamo che 22k + 1 (k3).

3) Dimostriamo che 2 2(k + 1) + 1.

Infatti, 2 = 222(2k + 1) =(2k + 3)(2k - 1) 2k + 3, poiché 2k – 10 per qualsiasi valore naturale di k. Pertanto, 22n + 1 per ogni n3.

Una nota sul metodo di induzione matematica.

La dimostrazione per induzione matematica si compone di due fasi.

lthpalcoscenico. Controlliamo se l'affermazione è vera e quando n = 1 (o a n =R, se stiamo parlando del metodo sopra descritto).

2 ° piano Supponiamo che l'affermazione sia vera quando n =K, e, in base a ciò, dimostriamo che è vero anche quando P = K+1.

Ognuna di queste fasi è importante a modo suo, considerando l'esempio P(x)=x 2 +x+41, siamo convinti che l'affermazione possa essere vera in alcuni casi particolari, ma non vera in generale. Questo esempio ci convince quanto è importante la seconda fase della dimostrazione utilizzando il metodo dell'induzione matematica. Se lo ometti, puoi giungere alla conclusione sbagliata.

Tuttavia, non si dovrebbe pensare che la prima fase sia meno importante della seconda. Ora darò un esempio che mostra a quale conclusione assurda si può arrivare se si omette la prima fase della dimostrazione.

"Teorema a." Per qualsiasi numero naturale n 2p +1 Anche.

Provamangiòci sonoO. Sia vero questo teorema per n =K, questo è il numero 2 K + 1 Anche. Dimostriamolo allora il numero 2(K+1)+ 1 anche anche.

Veramente, 2(K+1)+1 = (2 K+1 )+2.

Per presupposto il numero 2 K +1 è pari, e quindi anche la sua somma con il numero pari 2 è pari. Il teorema è “dimostrato”.

Se non ci fossimo dimenticati di verificare se il nostro “teorema” è vero e quando n = 1, non saremmo arrivati ​​a un simile “risultato”.

Esempi di applicazione del metodo dell'induzione matematica alla dimostrazione delle disuguaglianze.

Esempio 1. Dimostrare che per ogni numero naturale n1

.

Indichiamo il lato sinistro della disuguaglianza con .

Pertanto per n=2 vale la disuguaglianza.

Lascia che per alcuni k. Dimostriamolo allora e . Abbiamo , .

Confrontando e , abbiamo , cioè. .

Per ogni intero positivo k, il lato destro dell'ultima uguaglianza è positivo. Ecco perché . Ma questo significa anche.

Esempio 2. Trova l'errore nel ragionamento.

Dichiarazione. Per ogni numero naturale n la disuguaglianza è vera.

Prova.

Sia vera la disuguaglianza per n=k, dove k è un numero naturale, cioè

Proviamo che allora la disuguaglianza vale anche per n=k+1, cioè

Infatti, non meno di 2 per ogni k naturale. Aggiungiamo al lato sinistro della disuguaglianza (1) e al lato destro 2. Otteniamo la giusta disuguaglianza , o . L'affermazione è stata dimostrata.

Esempio 4:

Dimostrare la disuguaglianza

Dove x 1, x 2,…., x 3 sono numeri positivi arbitrari.

Questa importante disuguaglianza tra la media aritmetica e la media geometrica di n numeri è una semplice conseguenza della relazione dimostrata nell'esempio precedente. Infatti, siano x 1, x 2, ..., x n numeri positivi arbitrari. Considera n numeri

Ovviamente tutti questi numeri sono positivi e il loro prodotto è uguale a uno. Pertanto, secondo quanto dimostrato nell’esempio precedente, la loro somma è maggiore o uguale a n, cioè

≥n

e il segno di uguaglianza vale se e solo se x 1 = x 2 = ... = x n.

La disuguaglianza tra la media aritmetica e la media geometrica di n numeri risulta spesso utile per dimostrare altre disuguaglianze e per trovare i valori più piccoli e più grandi delle funzioni.

Applicazione del metodo dell'induzione matematica alla somma di serie.

Esempio 5. Dimostrare la formula

, n – numero naturale.

Quando n=1, entrambi i membri dell'uguaglianza diventano uno e, quindi, la prima condizione del principio di induzione matematica è soddisfatta.

Supponiamo che la formula sia corretta per n=k, cioè

.

Aggiungiamo a entrambi i lati di questa uguaglianza e trasformiamo il lato destro. Allora otteniamo

Quindi, dal fatto che la formula è vera per n=k, ne consegue che è vera anche per n=k+1. Questa affermazione è vera per qualsiasi valore naturale di k. Quindi è soddisfatta anche la seconda condizione del principio di induzione matematica. La formula è provata.

Esempio 6. Prova che .

Metodo di induzione matematica nella risoluzione di problemi di divisibilità.

Usando il metodo dell'induzione matematica, puoi dimostrare varie affermazioni riguardanti la divisibilità dei numeri naturali.

La seguente affermazione può essere dimostrata in modo relativamente semplice. Mostriamo come si ottiene utilizzando il metodo dell'induzione matematica.

Esempio 7. SeNè un numero naturale, allora il numero è pari.

Quando n=1 la nostra affermazione è vera: - un numero pari. Supponiamo che sia un numero pari. Poiché , a 2k è un numero pari, allora è pari. Quindi la parità è dimostrata per n=1, la parità si deduce dalla parità, ciò significa che è pari per tutti i valori naturali di n.

Esempio 8. Dimostrare la verità della frase

A(n)=(il numero 5 è un multiplo di 19), n è un numero naturale.

L'affermazione A(1)=(un numero divisibile per 19) è vera.

Supponiamo che per un certo valore n=k

A(k)=(numero divisibile per 19) è vero. Poi, da allora

Ovviamente anche A(k+1) è vero. Infatti, il primo termine è divisibile per 19 per l'assunzione che A(k) sia vera; anche il secondo termine è divisibile per 19 perché contiene un fattore 19. Entrambe le condizioni del principio di induzione matematica sono soddisfatte, quindi la proposizione A(n) è vera per tutti i valori di n.

Prova di identità

Esempio 9. Dimostralo per qualsiasi naturale N l'uguaglianza è vera

Q.E.D.

Esempio 10. Dimostrare l'identità

1) Verifichiamo che questa identità è vera per n = 1.

2) Sia vera l'identità per n = k, cioè

3) Proviamo che questa identità vale anche per n = k + 1, cioè

M – somma di 2) e 3).

Metodo di induzione matematica nella risoluzione di problemi di progressione geometrica

Esempio 11. Dimostriamo che il termine generale della progressione geometrica è uguale a

UN P = un 1 ∙ Q n-1 , mediante il metodo dell’induzione matematica.

n=1:

a1 = a1 ∙q 0

un 1 = un 1 ∙1

lato sinistro = lato destro.

n=K:

a k = a 1 ∙q k -1

n =K+1:

ak +1 = a1 ∙q k

Prova:

a k +1 = a k ∙q = a 1 ∙q k -1 ∙ q = a 1 ∙q k ,

Q.E.D.

Sono soddisfatte entrambe le condizioni del principio di induzione matematica e quindi la formula UN N = UN 1 ∙ Q N -1 vero per qualsiasi numero naturale P.

Problemi della realtà

Esempio 12:

Dimostriamo che la somma degli angoli interni di un n-gono convesso è uguale a π(n-2).

1. Il numero minimo di angoli è tre. Quindi cominciamo
dimostrazione con n = 3. Lo troviamo per un triangolo
la formula dà π (3~2) = π Dichiarazione per n = 3

Giusto.

2. Supponiamo che la formula
vero per n=k. Dimostriamolo
è vero per qualsiasi convesso
(a +1) -gon. Analizziamolo

(k +1) -gon diagonale

in modo da ottenere un k-gon e un triangolo (vedi figura).

Poiché la formula è vera per un triangolo e un k-gon, otteniamo π (k - 2) + π = π (k -1).

Otteniamo la stessa cosa se sostituiamo p = k + 1 nella formula originale: π (k +1 - 2) = π (k -1).

Compiti suggeriti per l'Esame di Stato Unificato.

Esempio 1.

Dimostrarlo per qualsiasi numero naturale pagina 9 n+1 - 20:00 – 9:00 multiplo di 16.

1) Verifichiamo che questa affermazione è vera quando n=1:

9 2 - 8 – 9 = 81- 8 – 9 = 64, 64 16.

A n=1 l'affermazione è vera.

2) Supponiamo che questa affermazione sia vera, quando n =K :

(9 K +1 - 8 K - 9) 16.

3) E dimostriamo che questa affermazione è vera per n =K+1 :

(9 K +2 – 8 (K+1) - 9) 16.

Prova:

9 K +2 - 8(K+1) – 9 =9 K +1 ∙ 9 1 - 8 K – 8 – 9 = 9 K + 1 ∙ 9 - 8 K – 17 =

= 9(9 K +1 - 8 K - 9) + 64 K + 64 = 9(9 K +1 - 8 K - 9) +64(K+1)=

= 9(9 K +1 – 8 K - 9)+ 64(K+1).

Quindi: ( 9(9 K +1 - 8 K - 9) + 64(K-1)) 16.

Quindi sono soddisfatte entrambe le condizioni del principio di induzione matematica, e quindi 9 k+1 - 8p-9 divisibile per 16 per qualsiasi naturale P.

Esempio 2.

P la condizione è soddisfatta:

1 3 +2 3 +3 3 +… N 3 =.

S N = .

Controlliamo che questa formula sia corretta quando n=1:

Lato sinistro = 1 3 =1

Lato destro =

La formula è corretta quando n=1.

N= K:

1 3 +2 3 +3 3 +… K 3 =.

S K =.

n=K+1:

1 3 +2 3 +3 3 +…+(K+1) 3 =.

S K +1 = .

Prova:

S K +1 = S K +(K+1) 3

Quindi, questa formula è vera in due casi ed è stata dimostrata vera in N= K+1 quindi è vero per qualsiasi numero naturale P.

Esempio 3.

Dimostrarlo per qualsiasi numero naturale P la condizione è soddisfatta:

1∙2∙3+2∙3∙4+…+ p(p+1)(p+2)=.

.

1) Verifichiamo che questa formula sia corretta quando n=1:

Lato sinistro = 1∙2∙3=6.

Parte destra = .

6 = 6; la condizione è vera quando n=1.

2) Supponiamo che questa formula sia corretta N= K:

1∙2∙3+2∙3∙4+…+ K(K+1)(K+2)=.

S K =.

3) E dimostriamo che questa formula è corretta N= K+1:

1∙2∙3+2∙3∙4+…+(K+1)(K+2)(K+3)=.

S K +1 =.

Prova:

Quindi, questa condizione è vera in due casi ed è stata dimostrata vera in N= K+1, quindi è vero per qualsiasi numero naturale P.

Esempio 4.

Dimostrare che è naturale P l'uguaglianza è vera

1) Quando n=1 otteniamo l'uguaglianza corretta

2) Fatta l'ipotesi di induzione, considerare la somma a sinistra dell'uguaglianza, con N= K+1;

3) Per completare la dimostrazione, notiamo che

Pertanto, l’uguaglianza è giusta.

Esempio 5.

Nell'aereo trattenuto P rette di cui nessuna due è parallela e nessuna tre passa per un punto. Determina in quante parti queste linee dividono il piano.

Dopo aver disegnato i disegni necessari, possiamo annotare la seguente corrispondenza tra i numeri P linee rette che soddisfano le condizioni del problema e il numero UN P parti in cui queste rette dividono il piano:

A giudicare dai primi termini, la sequenza UN Pè tale che le differenze UN 2 -UN 1 , UN 3 -UN 2 , UN 4 -UN 3 ,… formano una progressione aritmetica. Se usiamo l’esempio già discusso, possiamo ipotizzarlo P linee rette che soddisfano le condizioni del problema, dividono il piano in

parti. Questa formula è facile da verificare per i primi valori P, tuttavia, ovviamente, non ne consegue che esso fornisca una risposta al problema proposto. Questa affermazione richiede ulteriori prove utilizzando il metodo dell'induzione matematica.

Prendendoci una pausa dalla “selezione” appena effettuata, lo dimostriamo P le rette (di cui nessuna è parallela e nessuna passa per lo stesso punto) dividono il piano in UN P parti dove UN P calcolato dalla formula.

È ovvio che quando n=1 la formula è corretta. Avendo fatto l'ipotesi di induzione, consideriamo K+1 rette che soddisfano le condizioni del problema. Selezionandoli casualmente K linee rette, possiamo dire che dividono il piano in

parti. Aggiungiamo ora (K+1) - l'esima retta. Poiché non è parallela a nessuna delle linee precedenti, le intersecherà tutte K Dritto Poiché non passerà per nessuno dei punti di intersezione delle linee precedenti, passerà lungo K+1 pezzo in cui il piano è già stato diviso, e ciascuno di questi pezzi sarà diviso in due parti, cioè ne verranno aggiunti altri K+1 pezzi. Quindi il numero totale di pezzi in cui è diviso l'aereo K+1 dritto, sì

Questo completa la dimostrazione.

Conclusione

Quindi, l'induzione (dal latino inductio - guida, motivazione) è una delle forme di inferenza, una tecnica di ricerca, utilizzando la quale dalla conoscenza dei fatti individuali si arriva a disposizioni generali. L'induzione può essere completa o incompleta. Il metodo dell'induzione incompleta consiste nel passare a una formulazione universale dopo aver verificato la verità di formulazioni particolari per alcuni, ma non tutti, valori di n. Usando l'induzione completa, ci consideriamo autorizzati a dichiarare la verità di una formulazione universale solo quando siamo convinti della sua verità per ogni singolo valore di n. Il metodo dell'induzione matematica è un metodo di dimostrazione basato sul principio dell'induzione matematica. Permette, alla ricerca di una legge generale, di verificare ipotesi, scartare quelle false e affermare quelle vere.

Il metodo di induzione matematica è uno dei fondamenti teorici per risolvere problemi di somma, dimostrare identità, dimostrare e risolvere disuguaglianze, risolvere il problema della divisibilità, studiare le proprietà delle sequenze numeriche, risolvere problemi geometrici, ecc.

Dopo aver conosciuto il metodo dell'induzione matematica, ho studiato letteratura specializzata, consultato un insegnante, analizzato dati e soluzioni a problemi, utilizzato risorse Internet ed eseguito i calcoli necessari.

Conclusione:

Durante il lavoro, ho imparato che per risolvere i problemi utilizzando il metodo dell'induzione matematica, è necessario conoscere e comprendere il principio di base dell'induzione matematica.

Il vantaggio del metodo di induzione matematica è la sua versatilità, poiché molti problemi possono essere risolti utilizzando questo metodo. Lo svantaggio dell’induzione incompleta è che talvolta porta a conclusioni errate.

Avendo generalizzato e sistematizzato le conoscenze sull'induzione matematica, mi sono convinto della necessità di conoscere l'argomento "metodo di induzione matematica". Inoltre, questa conoscenza aumenta l’interesse per la matematica come scienza.

Inoltre durante il lavoro ho acquisito competenze nella risoluzione di problemi utilizzando il metodo dell'induzione matematica. Credo che queste competenze mi aiuteranno in futuro.

Bibliografia.

1. Bokovnev O. A., Firsov V. V., Shvartsburd S. I. Domande selezionate di matematica. 9° grado. Corso facoltativo - M.: Educazione, 1979.

2. Vilenkin N. Ya., Shibasov L. P., Shibasova Z. F. Dietro le pagine di un libro di testo di matematica. Mosca: Istruzione, 1996.

3. Galitsky M. L., Moshkovich M. M., Shvartsburd S. I. Studio approfondito del corso di algebra e analisi matematica: raccomandazioni metodologiche, materiali didattici.

4.Ivlev B.M., Abramov A.M., Dudnitsin Yu.P., Shvartsburd S.I. M.: Educazione, 1990.

5. Petrakov I. S. Club matematici nelle classi 8-10: libro. per gli insegnanti M.: Prosveshchenie, 1987.

6. Sharygin I.F. Corso facoltativo di matematica. Libro di testo per la risoluzione dei problemi per la scuola superiore del 10° grado - M.: Prosveshchenie, 1989.

Attenzione studenti! I corsi vengono completati in modo indipendente in stretta conformità con l'argomento scelto. Non sono ammessi argomenti duplicati! Si prega di comunicare al docente l'argomento prescelto in qualsiasi modo sia conveniente, individualmente o in un elenco indicando il nome completo, il numero del gruppo e il titolo del lavoro del corso.

Argomenti di esempio per i corsi della disciplina
"Logica matematica"

1. Il metodo risolutivo e sue applicazioni in algebra proposizionale e algebra dei predicati.

2. Sistemi assiomatici.

3. CNF e DNF minimi e più brevi.

4. Applicazione dei metodi della logica matematica alla teoria dei linguaggi formali.

5. Grammatiche formali come calcoli logici.

6. Metodi per risolvere problemi di logica testuale.

7. Sistemi di programmazione logica.

8. Gioco di logica.

9. Indecidibilità della logica del primo ordine.

10. Modelli aritmetici non standard.

11. Metodo della diagonalizzazione in logica matematica.

12. Macchine di Turing e tesi di Church.

13. Calcolabilità sull'abaco e funzioni ricorsive.

14. Rappresentabilità di funzioni ricorsive e risultati negativi della logica matematica.

15. Risolvibilità dell'aritmetica delle addizioni.

16. Logica del secondo ordine e definibilità in aritmetica.

17. Il metodo degli ultraprodotti nella teoria dei modelli.

18. Teorema di Gödel sull'incompletezza dell'aritmetica formale.

19. Teorie assiomatiche risolvibili e indecidibili.

20. Lemma di interpolazione di Craig e sue applicazioni.

21. I più semplici convertitori di informazioni.

22. Circuiti di commutazione.

24. Strutture di contatto.

25. Applicazione di funzioni booleane ai circuiti di contatti di relè.

26. Applicazione delle funzioni booleane nella teoria del riconoscimento di pattern.

27. Logica matematica e sistemi di intelligenza artificiale.

Il lavoro del corso deve consistere di 2 parti: il contenuto teorico dell'argomento e una serie di problemi sull'argomento (almeno 10) con soluzioni. È inoltre consentito scrivere una tesina di tipo ricerca, sostituendo la seconda parte (risolvere problemi) con uno sviluppo indipendente (ad esempio un algoritmo funzionante, un programma, un campione, ecc.) creato sulla base del materiale teorico discusso nella prima parte del lavoro.

1) Barwise J. (a cura di) Libro di consultazione sulla logica matematica. - M.: Nauka, 1982.

2) Fratelli dei linguaggi di programmazione. - M.: Nauka, 1975.

3) Boulos J., computabilità e logica. - M.: Mir, 1994.

4) Logica Hindikin nei problemi. - M., 1972.

5), Logica della Palyutina. - M.: Nauka, 1979.

6) Risolvibilità di Ershov e modelli costruttivi. - M.: Nauka, 1980.

7), Teoria di Taitslin // Uspekhi Mat. Nauk, 1965, 20, No. 4, p. 37-108.

8) Igoshin - seminario sulla logica matematica. - M.: Educazione, 1986.

9) Logica di Igoshin e teoria degli algoritmi. - Saratov: casa editrice Sarat. Università, 1991.

10) In Ts., utilizzando Turbo Prolog. - M.: Mir, 1993.

11) introduzione alla metamatematica. - M., 1957.

12) logica atematica. - M.: Mir, 1973.

13) logica nella risoluzione dei problemi. - M.: Nauka, 1990.

14) Logica di Kolmogorov: un libro di testo per la matematica universitaria. specialità /, - M.: Casa editrice URSS, 2004. - 238 p.

15) storia con nodi / Trad. dall'inglese - M., 1973.

16) Gioco di logica / Trans. dall'inglese - M., 1991.

17), Maksimov sulla teoria degli insiemi, logica matematica e teoria degli algoritmi. - 4a ed. - M., 2001.

18), Logica di Sukacheva. Corso di lezioni. Libro di problemi pratici e soluzioni: guida allo studio. 3a ed., rev. - San Pietroburgo.

19) Casa editrice “Lan”, 2008. - 288 p.

20) Lyskova in informatica / , . - M.: Laboratorio delle conoscenze di base, 2001. - 160 p.

21) Logica matematica / Sotto la direzione generale e altri - Minsk: Scuola superiore, 1991.

22) introduzione alla logica matematica. - M.: Nauka, 1984.

23) Moshchensky sulla logica matematica. -Minsk, 1973.

24) Nikolskaya con logica matematica. - M .: Istituto psicologico e sociale di Mosca: Flint, 1998. - 128 p.

25) Logica Nikolskaya. - M., 1981.

26) Logica matematica di Novikov. - M.: Nauka, 1973.

27) Teoria di Rabin. Nel libro: Libro di consultazione sulla logica matematica, parte 3. Teoria della ricorsione. - M.: Nauka, 1982. - p. 77-111.

28) Tey A., Gribomon P. et al.Approccio logico all'intelligenza artificiale. T. 1. - M.: Mir, 1990.

29) Tey A., Gribomon P. et al.Approccio logico all'intelligenza artificiale. T. 2. - M.: Mir, 1998.

30) Chen Ch., Li R. Logica matematica e dimostrazione automatica di teoremi. - M.: Nauka, 1983.

31) introduzione alla logica matematica. - M.: Mir, 1960.

32) Logica di Shabunin. Logica proposizionale e logica dei predicati: libro di testo /, rep. ed. ; Stato ciuvascia Università intitolata a . - Cheboksary: ​​casa editrice ciuvascia. Università, 2003. - 56 p.