Storia dell'origine della teoria dei grafi. Storia dell'emergere e dello sviluppo della teoria dei grafi. Teoria dei grafi e principali problemi applicati moderni

GRAFICI

Molti problemi si riducono alla considerazione di un insieme di oggetti, le cui proprietà essenziali sono descritte dalle connessioni tra loro. Ad esempio, guardando una mappa stradale, ci si potrebbe interessare solo se esiste una connessione tra determinati insediamenti, ignorando la configurazione e la qualità delle strade, le distanze e altri dettagli. Quando si studiano i circuiti elettrici, può venire in primo piano la natura delle connessioni dei suoi vari componenti: resistori, condensatori, sorgenti, ecc.. Le molecole organiche formano strutture le cui proprietà caratteristiche sono le connessioni tra atomi. Di interesse possono essere varie connessioni e relazioni tra persone, eventi, stati e, in generale, tra qualsiasi oggetto.

In questi casi è conveniente rappresentare gli oggetti in esame come punti e le connessioni tra loro come linee di configurazione arbitraria. Un'immagine così formalizzata è chiamata grafico (dal greco grajw - scrivo).

Riso. 4.1 .

Il primo lavoro sui grafici fu pubblicato dal ventenne Leonhard Euler nel 1736, mentre lavorava all'Accademia russa delle scienze. Conteneva una soluzione al problema dei ponti di Königsberg (Fig. 4.1a): è possibile fare una passeggiata in modo tale che, lasciando qualsiasi punto della città, si possa ritornarvi camminando esattamente una volta su ciascun ponte ? È chiaro che, a seconda delle condizioni del problema, non importa come il percorso attraversi parti del territorio a, b, c, d, su cui si trova la città di Koenigsberg (ora Kaliningrad), quindi possono essere rappresentati come vertici. E poiché le connessioni tra queste parti vengono effettuate solo tramite sette ponti, ciascuno di essi è rappresentato da un bordo che collega i vertici corrispondenti. Di conseguenza, otteniamo il grafico mostrato in Fig. 4.1b. Eulero diede una risposta negativa alla domanda posta. Inoltre, dimostrò che tale percorso esiste solo per un grafo tale che ciascuno dei suoi vertici è connesso ad un numero pari di archi.

La teoria dei grafi ricevette il suo successivo impulso quasi 100 anni dopo con lo sviluppo della ricerca sulle reti elettriche, sulla cristallografia, sulla chimica organica e su altre scienze. Insieme a numerosi enigmi e giochi di grafici, sono stati presi in considerazione importanti problemi pratici, molti dei quali richiedevano sofisticate tecniche matematiche. Già a metà del secolo scorso Kirchhoff usò i grafici per analizzare i circuiti elettrici e Cayley esplorò un'importante classe di grafici per identificare ed elencare gli isomeri degli idrocarburi saturi. Tuttavia, la teoria dei grafi come disciplina matematica si è formata solo a metà degli anni Trenta del secolo scorso grazie al lavoro di molti ricercatori, il merito più grande tra i quali appartiene a D. Koenig. Contributi significativi alla teoria dei grafi furono apportati dagli scienziati sovietici L. S. Pontryagin, A. A. Zykov, V. G. Vising e altri.

Senza nemmeno accorgercene, incontriamo continuamente grafici. Ad esempio, un grafico è un diagramma delle linee della metropolitana. I punti su di esso rappresentano le stazioni e le linee rappresentano i percorsi ferroviari. Ricercando i nostri antenati e facendoli risalire ai nostri antenati, costruiamo un albero genealogico. E questo albero è un grafico.

I grafici servono come mezzo conveniente per descrivere le relazioni tra gli oggetti. Ad esempio, considerando un grafico che rappresenta una rete di strade tra aree popolate, è possibile determinare il percorso dal punto A al punto B. Se esistono diversi percorsi di questo tipo, si vorrebbe scegliere quello ottimale in un certo senso, ad esempio il più breve o il più sicuro. Per risolvere il problema della selezione è necessario effettuare alcuni calcoli sui grafici. Quando si risolvono tali problemi, è conveniente utilizzare tecniche algebriche e il concetto stesso di grafico deve essere formalizzato.

La teoria dei grafi ha un potente strumento per risolvere problemi applicati in un'ampia varietà di campi della scienza e della tecnologia. Ciò include, ad esempio, l'analisi e la sintesi di circuiti e sistemi, la progettazione di canali di comunicazione e lo studio dei processi di trasferimento delle informazioni, la costruzione di circuiti di contatto e lo studio di macchine a stati finiti, la pianificazione e controllo di reti, la ricerca operativa, la selezione di percorsi e flussi ottimali nelle reti, studio di processi casuali e molti altri compiti. La teoria dei grafi è strettamente correlata a rami della matematica discreta come la teoria degli insiemi, la teoria delle matrici, la logica matematica e la teoria della probabilità.

Attualmente la teoria dei grafi copre molto materiale, ma nel presentarla ci limiteremo solo a una parte di esso e, tralasciando numerosi teoremi, ne prenderemo in considerazione solo alcuni concetti basilari.

Leonard Euler è considerato il fondatore della teoria dei grafi. Nel 1736, in una delle sue lettere, formulò e propose una soluzione al problema dei sette ponti di Königsberg, che in seguito divenne uno dei problemi classici della teoria dei grafi.

I primi problemi nella teoria dei grafi riguardavano la risoluzione di problemi matematici ricreativi e di enigmi. Ecco una rivisitazione di un estratto dalla lettera di Eulero datata 13 marzo 1736: “Mi è stato posto un problema su un'isola situata nella città di Königsberg e circondata da un fiume attraversato da 7 ponti. La questione è se qualcuno possa aggirarli continuamente, passando solo una volta su ciascun ponte. E poi mi è stato detto che nessuno era ancora riuscito a farlo, ma nessuno aveva dimostrato che fosse impossibile. Questa questione, per quanto banale, mi è sembrata tuttavia degna di attenzione in quanto né la geometria, né l'algebra, né l'arte combinatoria sono sufficienti a risolverla. Dopo aver riflettuto a lungo, ho trovato una regola semplice, basata su una dimostrazione del tutto convincente, con l'aiuto della quale è possibile, in tutti i problemi di questo tipo, determinare immediatamente se una tale deviazione può essere fatta attraverso un numero qualsiasi e un numero qualsiasi di ponti localizzati in qualsiasi modo o meno.” I ponti di Königsberg possono essere rappresentati schematicamente come segue:

Regola di Eulero:

1. In un grafo che non ha vertici di grado dispari, c'è un attraversamento di tutti gli spigoli (e ogni spigolo viene attraversato esattamente una volta) a partire da qualsiasi vertice del grafico.

2. In un grafo che ha due e solo due vertici con gradi dispari, c'è una traversata che inizia in un vertice con grado dispari e termina nell'altro.

3. In un grafo che ha più di due vertici con gradi dispari, tale attraversamento non esiste.

Esiste un altro tipo di problema relativo allo spostamento lungo i grafici. Stiamo parlando di problemi in cui è necessario trovare un percorso che passi per tutti i vertici e non più di una volta per ciascuno. Un ciclo che passa per ciascun vertice una e una sola volta è chiamato retta hamiltoniana (dal nome di William Rowan Hamilton, il famoso matematico irlandese del secolo scorso che fu il primo a studiare tali rette). Sfortunatamente, non è stato ancora trovato un criterio generale con l'aiuto del quale si possa decidere se un dato grafico è hamiltoniano e, in tal caso, trovare tutte le linee hamiltoniane su di esso.

Formulato a metà del XIX secolo. Anche il problema dei quattro colori sembra un problema divertente, ma i tentativi di risolverlo hanno portato ad alcuni studi sui grafici che hanno significato teorico e applicato. Il problema dei quattro colori è formulato come segue: "È possibile colorare un'area di qualsiasi mappa piatta con quattro colori in modo che due aree adiacenti qualsiasi siano colorate con colori diversi?" L'ipotesi che la risposta sia affermativa fu formulata a metà del XIX secolo. Nel 1890 fu dimostrata un'affermazione più debole, vale a dire che qualsiasi mappa piatta può essere colorata in cinque colori. Associando una qualunque mappa planare al suo grafo planare duale, otteniamo una formulazione equivalente del problema in termini di grafi: è vero che il numero cromatico di qualunque grafo planare è minore o uguale a quattro? Numerosi tentativi di risolvere il problema hanno influenzato lo sviluppo di una serie di aree della teoria dei grafi. Nel 1976 fu annunciata una soluzione positiva al problema utilizzando un computer.

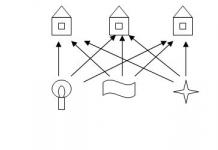
Un altro vecchio problema topologico che è stato a lungo particolarmente resistente alla soluzione e che ha tormentato le menti degli amanti dei puzzle è noto come “problema dell’approvvigionamento di elettricità, gas e acqua”. Nel 1917 Henry E. Dudeney gli diede questa formulazione. Gas, elettricità e acqua devono essere installati in ciascuna delle tre case mostrate in figura.

Teoria dei grafi. 1

La storia dell'emergere della teoria dei grafi. 1

La regola di Eulero. 1

Letteratura

1. Teoria dei grafi di Belov, Mosca, "Scienza", 1968.

2. Nuove tecnologie pedagogiche e informatiche E.S. Polat , Mosca, "Accademia" 1999

3. Kuznetsov O.P., Adelson-Velsky G.M. Matematica discreta per l'ingegnere. – M.: Energoatomizdat, 1988.

4. Cook D., Baze G. Matematica informatica. – M.: Scienza, 1990.

5. Nefedov V.N., Osipova V.A. Corso di matematica discreta. – M.: Casa editrice MAI, 1992.

6. Minerale O. Teoria dei grafi. – M.: Scienza, 1980.

7. Ismagilov R.S., Kalinkin A.V. Materiali per le lezioni pratiche del corso: Matematica Discreta

Teoria dei grafi- capitolo matematica discreta, studiando le proprietà grafici . In senso generale, un grafo è rappresentato come un insieme di vertici (nodi) collegati da spigoli. In una definizione rigorosa, tale coppia di insiemi è chiamata grafico. G=(V,E), dove V è un sottoinsieme di qualsiasi insieme numerabile ed E è un sottoinsieme di V×V.

Storia della teoria dei grafi
Leonard Euler è considerato il fondatore della teoria dei grafi. Nel 1736, in una delle sue lettere, formulò e propose una soluzione al problema dei sette ponti di Königsberg, che in seguito divenne uno dei problemi classici della teoria dei grafi.
I primi problemi nella teoria dei grafi riguardavano la risoluzione di problemi matematici ricreativi e di enigmi. Ecco una rivisitazione di un estratto dalla lettera di Eulero datata 13 marzo 1736: “Mi è stato posto un problema su un'isola situata nella città di Königsberg e circondata da un fiume attraversato da 7 ponti. La questione è se qualcuno possa aggirarli continuamente, passando solo una volta su ciascun ponte. E poi mi è stato detto che nessuno era ancora riuscito a farlo, ma nessuno aveva dimostrato che fosse impossibile. Questa questione, per quanto banale, mi è sembrata tuttavia degna di attenzione in quanto né la geometria, né l'algebra, né l'arte combinatoria sono sufficienti a risolverla. Dopo aver riflettuto a lungo, ho trovato una regola semplice, basata su una dimostrazione del tutto convincente, con l'aiuto della quale è possibile, in tutti i problemi di questo tipo, determinare immediatamente se una tale deviazione può essere fatta attraverso un numero qualsiasi e un numero qualsiasi di ponti localizzati in qualsiasi modo o meno.” I ponti di Königsberg possono essere rappresentati schematicamente come segue:
Regola di Eulero:

1. In un grafico che non ha vertici di gradi dispari, c'è un attraversamento di tutti gli spigoli (e ogni spigolo viene attraversato esattamente una volta) a partire da qualsiasi vertice del grafico.
2. In un grafo che ha due e solo due vertici con gradi dispari, c'è una traversata che inizia in un vertice con grado dispari e termina nell'altro.
3. In un grafo che ha più di due vertici con gradi dispari, tale attraversamento non esiste.

Anno scolastico 2016 Anno

1. Introduzione

2. Storia dell'emergere della teoria dei grafi

3. Concetti base della teoria dei grafi

4. Teoremi fondamentali della teoria dei grafi

5. Metodi di rappresentazione dei grafici in un computer

6. Richiami su problemi di teoria dei grafi

7. Conclusione

8. Riferimenti

introduzione

Recentemente, la ricerca in aree tradizionalmente legate alla matematica discreta è diventata sempre più importante. Insieme a sezioni classiche della matematica come l'analisi matematica e le equazioni differenziali, nei curricula della specialità "Matematica applicata" e in molte altre specialità sono apparse sezioni sulla logica matematica, l'algebra, la combinatoria e la teoria dei grafi. Le ragioni di ciò non sono difficili da comprendere semplicemente individuando la gamma di problemi risolvibili sulla base di questo apparato matematico.

La storia dell'emergere della teoria dei grafi.

1. Problema sui ponti di Königsberg. Nella fig. 1 mostra una pianta schematica della parte centrale della città di Koenigsberg (ora Kaliningrad), comprese due sponde del fiume Pergola, due isole al suo interno e sette ponti di collegamento. Il compito è percorrere tutte e quattro le parti del territorio, attraversando ogni ponte una volta e tornare al punto di partenza. Questo problema fu risolto (fu dimostrato che non esisteva soluzione) da Eulero nel 1736.

riso. 1

2. Il problema delle tre case e dei tre pozzi. Ci sono tre case e tre pozzi, in qualche modo situati su un piano. Disegna un percorso da ciascuna casa a ciascun pozzo in modo che i percorsi non si intersechino (Fig. 2). Questo problema fu risolto (è stato dimostrato che non esiste soluzione) da Kuratovsky nel 1930.

riso. 2

3. Il problema dei quattro colori. La divisione di un piano in aree non sovrapposte è chiamata mappa. Le aree su una mappa sono chiamate adiacenti se hanno un confine comune. Il compito è colorare la mappa in modo tale che non ci siano due aree adiacenti dello stesso colore (Fig. 3). Dalla fine del secolo scorso è nota l'ipotesi che quattro colori siano sufficienti per questo. Nel 1976, Appel e Heiken pubblicarono una soluzione al problema dei quattro colori, basata su una ricerca al computer. La soluzione “programmatica” a questo problema è stato un precedente che ha dato luogo ad un acceso dibattito, che non è affatto terminato. L'essenza della soluzione pubblicata è provare un numero ampio ma finito (circa 2000) di potenziali controesempi al teorema dei quattro colori e dimostrare che nessun singolo caso è un controesempio. Questa ricerca è stata completata dal programma in circa mille ore di funzionamento del supercomputer. È impossibile verificare "manualmente" la soluzione risultante: la portata dell'enumerazione va ben oltre le capacità umane. Molti matematici sollevano la domanda: una simile “dimostrazione del programma” può essere considerata una dimostrazione valida? Dopotutto, potrebbero esserci degli errori nel programma... I metodi per dimostrare formalmente la correttezza dei programmi non sono applicabili a programmi di complessità come quello in discussione. Il test non può garantire l'assenza di errori e in questo caso è generalmente impossibile. Pertanto, possiamo solo fare affidamento sulle capacità di programmazione degli autori e credere che abbiano fatto tutto bene.

Riso. 3

Concetti di base della teoria dei grafi

1) Grafico G(V,E)è una raccolta di due insiemi: un insieme non vuoto V (insieme di vertici) e un insieme E di sottoinsiemi di due elementi dell'insieme V (E – insieme di archi).

2) Orientataè un grafico in cui è un insieme di coppie ordinate di vertici della forma (x,y), dove x è chiamato l'inizio e y è la fine dell'arco. L'arco (x, y) è spesso scritto come . Dicono anche che l'arco va dal vertice x al vertice y, e al vertice y adiacente con vertice x.

3) Se un elemento dell'insieme E può essere una coppia identico elementi (non distinti) di V, allora tale elemento dell'insieme è chiamato E ciclo continuo, e il grafico viene chiamato grafico con loop(O pseudografo).

4) Se E non è un insieme, ma impostato contenente diversi elementi identici, questi elementi vengono chiamati bordi multipli, e il grafico viene chiamato multigrafo.

5) Se gli elementi dell'insieme E non sono necessariamente due elementi, ma qualsiasi sottoinsieme dell'insieme V, allora tali elementi dell'insieme E sono chiamati iperarchi, e il grafico viene chiamato ipergrafo.

6) Se la funzione è specificata F: V → M e/o F: Mi → M, quindi l'insieme M chiamato insieme Appunti, e il grafico viene chiamato segnato(O caricato). L'insieme dei simboli è solitamente costituito da lettere o numeri interi. Se la funzione Fè iniettivo, cioè diversi vertici (spigoli) hanno etichette diverse, quindi il grafo viene chiamato numerato.

7) Sottografoè chiamato grafo G′(V′,E′), dove e/o .

a) Se V′ = V, allora si dice G′ nucleo sottografo G.

b) Se , allora si chiama il grafo G′ Proprio sottografo del grafico G.

c) Un sottografo G′(V′,E′) è detto sottografo regolare del grafo G(V,E) se G′ contiene tutti i possibili archi di G.

8) Grado (valenza) vertici è il numero di bordi incidenti a questo vertice (il numero di vertici adiacenti ad esso).

9) Itinerario in un grafico è una sequenza alternata di vertici e spigoli in cui due elementi adiacenti sono incidenti.

a) Se , allora il percorso Chiuso, Altrimenti aprire.

b) Se tutti i bordi sono diversi, viene chiamato il percorso catena.

c) Se tutti i vertici (e quindi gli spigoli) sono diversi, allora viene chiamato il percorso catena semplice.

d) Si chiama circuito chiuso ciclo.

e) Si dice un circuito chiuso semplice ciclo semplice.

f) Si chiama un grafo senza cicli aciclico.

g) Per i digrafi la catena si chiama di, e il ciclo è contorno.

riso. 4. Percorsi, catene, cicli

Esempio

Nel grafico, il cui diagramma è mostrato in Fig. 4:

1. v 1, v 3, v 1, v 4 – un percorso, ma non un circuito;

2. v 1, v 3, v 5, v 2, v 3, v 4 – una catena, ma non una catena semplice;

3. v 1, v 4, v 3, v 2, v 5 – catena semplice;

4. v 1, v 3, v 5, v 2, v 3, v 4, v 1 – un ciclo, ma non un ciclo semplice;

5. v 1 , v 3 , v 4 , v 1 – un ciclo semplice.

10) Se un grafico ha un ciclo (non necessariamente semplice) contenente tutti gli spigoli del grafico una volta, allora tale ciclo è chiamato Euleriano ciclo.

11) Se un grafo ha un ciclo semplice contenente tutti i vertici del grafo (uno alla volta), allora tale ciclo viene chiamato Hamiltoniano ciclo.

12) albero chiamato grafo connesso senza cicli.

13) scheletro Si chiama albero contenente tutti i vertici di un grafo.

14) Corrispondenzaè un insieme di archi in cui non ce ne sono due adiacenti.

15) L'abbinamento è chiamato massimo, se nessun suo superinsieme è indipendente.

16) Due vertici in un grafico collegato, se esiste una catena semplice che li collega.

17) Si chiama un grafo in cui tutti i vertici sono collegati coerente.

18) Si chiama un grafo formato solo da vertici isolati abbastanza incoerente.

19) Lunghezza del percorso viene chiamato il numero di bordi in esso contenuti (con ripetizioni).

20) Distanza tra i vertici u e v è detta lunghezza della catena più corta, e viene detta la catena più corta stessa geodetico.

21) Diametro di un grafico G è detta lunghezza della geodetica più lunga.

22) Eccentricità il vertice v in un grafo connesso G(V,E) è la distanza massima dal vertice v agli altri vertici del grafo G.

23) Raggio di un grafo G è detta la più piccola delle eccentricità dei vertici.

24) Si chiama vertice v centrale, se la sua eccentricità coincide con il raggio del grafico.

25) L'insieme dei vertici centrali si chiama centro grafico.

riso. 5 Eccentricità dei vertici e dei centri dei grafici (evidenziati).

Informazioni correlate.

La teoria dei grafi trova applicazione, ad esempio, nei sistemi di informazione geografica (GIS). Le case, le strutture, gli isolati, ecc. esistenti o di nuova progettazione sono considerati vertici e le strade, le reti di servizi, le linee elettriche, ecc. che li collegano sono considerati come bordi. L'utilizzo di vari calcoli eseguiti su tale grafico consente, ad esempio, di trovare la deviazione più breve o il negozio di alimentari più vicino, oppure di pianificare il percorso ottimale.

La teoria dei grafi contiene un gran numero di problemi irrisolti e di ipotesi non ancora dimostrate.

Storia della teoria dei grafi

Leonard Euler è considerato il fondatore della teoria dei grafi. Nel 1736, in una delle sue lettere, formulò e propose una soluzione al problema dei sette ponti di Königsberg, che in seguito divenne uno dei problemi classici della teoria dei grafi. Il termine "grafico" fu coniato per la prima volta da Sylvester, James Joseph nel 1878 nel suo articolo su Nature [ ] .

Terminologia della teoria dei grafi

Applicazione della teoria dei grafi

Guarda anche

Appunti

Letteratura

• Distel R. Teoria dei grafi Trad. dall'inglese - Novosibirsk: Casa editrice dell'Istituto di Matematica, 2002. - 336 p. ISBN 5-86134-101-X.
• Diestel R. Teoria dei grafi, edizione elettronica. - NY: Springer-Verlag, 2005. - P. 422.
• Basaker R., Saati T. Grafi e reti finiti. M.: Nauka, 1974. 368c.
• Belov V.V., Vorobiev E.M., Shatalov V.E. Teoria dei grafi. - M.: Più in alto. scuola, 1976. - P. 392.
• Berge K. Teoria dei grafi e sue applicazioni. M.: IL, 1962. 320c.
• Emelichev V. A., Melnikov O. I., Sarvanov V. I., Tyshkevich R. I. Lezioni di teoria dei grafi. M.: Nauka, 1990. 384 p. (Ed. 2, riveduto M.: URSS, 2009. 392 p.)