Such factors include: the value of U0, molecular mass of the polymer, the density of the spatial network, the size of substituents and temperature.
Potential rotation barrier (U0). The value of U0 depends on intra- and intermolecular interactions. Let us consider the factors affecting U0 and chain flexibility in carbon chain polymers.
In carbon-chain polymers, the least polar are saturated hydrocarbons. Their intra- and intermolecular interactions are small, and the values of U0 and ΔU are small, therefore the polymers have great kinetic and thermodynamic flexibility. Examples: PE, PP, PIB.
U0 values are especially low for polymers in the chain of which there is a double bond next to the single bond.
–CH2–CH=CH–CH2– Polybutadiene
The introduction of substituents containing polar groups into macromolecules leads to intra- and intermolecular interactions. In this case, the degree of polarity of the groups and the symmetry of their arrangement significantly influence:
The most polar groups are –СN, –NO2 (μ=3.4 D)
Less polar groups –Cl, –OH (μ=1.8-1.9 D)
When introducing polar groups, there are three possible effects on flexibility:
1. Polar groups are closely located and strong interactions are possible between them. The transition of such polymers from one spatial position to another requires overcoming large U0, therefore the chains of such polymers are the least flexible.
2. Polar groups are rarely located in the chain and interactions between them do not appear. The values of U0 and ΔU are small and the polymers have greater kinetic and thermodynamic flexibility.
3. Polar groups are arranged so that the electric fields cancel each other. In this case, the total dipole moment of the macromolecule is equal to zero. Therefore, the values of U0 and ΔU are low and the polymers have greater kinetic and thermodynamic flexibility.
Polytetrafluoroethylene –СF2–СF2–
Heterochain polymers
In heterochain polymers, rotation is possible around the C–O, C–N, Si–O, and C–C bonds. The U0 values for these bonds are small and the chains have sufficient kinetic flexibility. Examples: polyesters, polyamides, polyurethanes, silicone rubbers.
However, the flexibility of heterochain polymers may be limited by intermolecular interactions due to the formation of H-bonds (for example, cellulose, polyamides). Cellulose is one of the rigid chain polymers. It contains a large number of polar groups (–OH) and therefore cellulose is characterized by intra- and intermolecular interactions, high U0 values and low flexibility.
Molecular weight of the polymer. An increase in the molecular weight of the polymer increases the chain folding and therefore long macromolecules have greater kinetic flexibility compared to short macromolecules. As the MW increases, the number of conformations that a macromolecule can take increases and the flexibility of the chains increases.
Density of the spatial grid. The more chemical bonds between macromolecules, the less flexibility of the chains, i.e. As the density of the spatial grid increases, flexibility decreases. An example is the decrease in chain flexibility with an increase in the number of crosslinks in the resol series<резитол<резит.
Effect of size and number of substituents. An increase in the number of polar and large substituents reduces the mobility of macromolecule units and reduces kinetic flexibility. An example is the decrease in the flexibility of macromolecules of a copolymer of butadiene and styrene with an increase in the content of bulky phenyl substituents in the chain. If there are two substituents at one carbon atom in the polymer backbone (for example, OCH3 and CH3 in PMMA units), then the macromolecule becomes kinetically rigid.
Temperature. As the temperature increases, the kinetic energy of the macromolecule increases. As long as the kinetic energy value is less than U0, the chains undergo torsional vibrations. When the kinetic energy of the macromolecule becomes equal to or exceeds the value U0, the links begin to rotate. With increasing temperature, the value of U0 changes little, but the speed of rotation of the links increases and the kinetic flexibility increases.
Chemical transformations of macromolecules are used to obtain new polymers and modify the properties of finished polymers. Such transformations can be carried out both directionally and spontaneously during the synthesis, processing and operation of polymers under the influence of light, atmospheric oxygen, heat and mechanical influences. The main types of chemical transformations of polymers are:
1) Reactions that occur without changing the degree of polymerization (intramolecular and polymer-analogous transformations),
2) Reactions leading to an increase in the degree of polymerization (cross-linking and hardening of polymers, production of block and graft copolymers),
3) Reactions leading to a decrease in the degree of polymerization (destruction of polymers).
Features of chemical reactions of polymers
Chemical reactions of polymers do not differ from classical organic reactions, however, due to the large size of macromolecules and the complexity of their structure, polymer reactions have specific features.
The main differences between polymer reactions and reactions of low molecular weight compounds are:
For polymers, reactions are possible that are not typical for low-molecular-weight compounds, for example, depolymerization. Depolymerization is the sequential elimination of monomer units from the chain.
Unlike reactions of low molecular weight compounds, when the final and intermediate products of reactions can be separated from the starting compounds, in the case of reactions of polymers, the final and intermediate products are part of the same macromolecule and cannot be separated. For example, in the esterification of a low molecular weight alcohol, at each stage of the reaction the system contains alcohol, acid, ester and water, which can be separated. When esterifying polyvinyl alcohol, the intermediate reaction products are copolymers containing hydroxyl and ester groups that cannot be separated:
The reactivity of functional groups of macromolecules differs from the reactivity of low molecular weight compounds. The reason is the chain nature of the polymer, when Flory's “principle of equal reactivity” is not respected. The idea that the reactivity of functional groups should not depend on the length of the polymer chain is outdated.
The main features in the chemical behavior of polymers in comparison with low-molecular analogues are configurational, conformational, and concentration.
Supramolecular, electrostatic and neighbor effects.
Configuration effect - this is the difference in the environment of the functional groups of the polymer at the beginning and at the end of the reaction, which affects the direction and completion of the reaction, the kinetics and mechanism of the reaction.
The reactivity of polymers during chemical transformations is significantly influenced by chain stereoisomerism. For example, cis-isomer - natural rubber differs during chemical transformations from trance-isomer – gutta-percha. The arrangement of functional groups along the chain length also affects their chemical properties. For example, PVA macromolecules of a “normal” structure (connection of units of the “head to tail” type) are not subject to destruction under the influence of oxygen and periodic acid (HIO4), but macromolecules of PVA of an abnormal structure (connection of units of the “head to head” type) are easily destroyed .
Another example, when the links in the PVC chain are arranged “head to tail”, dehydrochlorination and thermal decomposition of macromolecules proceeds slowly, and when the links in the chain are arranged “head to head”, the reaction proceeds quickly.
PVC Polychloroprene
“Neighbor effect" . In polymers, a change in the reactivity of functional groups or units under the influence of an already reacted group located nearby is called the “neighbor effect”. The influence of “neighbors” causes changes in the rate and mechanism of reactions in polymers. In this case, the reaction rate can increase by 103–104 times. Along with the accelerating effect, “neighbors” can also have an inhibitory effect on the reaction rate.
3. Molecular weight of polymers and molecular weight distribution (MWD). Polydispersity of polymers. Number-average, viscosity-average and weight-average molecular weight of polymers. Methods for determining the molecular weights of polymers.
Most synthetic polymers consist of macromolecules of varying lengths, i.e. are polydisperse due to the statistical (random) nature of elementary synthesis reactions and the possibility of destruction of macromolecules. Biopolymers are usually homogeneous in molecular weight (MM), but when polymers are isolated, some bonds are broken and the biopolymers become polydisperse.
Due to polydispersity, polymers are characterized by average MM and, depending on the type of averaging, they are distinguished number average And mass average MM. There are other types of averaging, so when studying the hydrodynamic properties of polymers they determine medium hydrodynamic MM . Such MMs are determined by measuring viscosity ( average viscosity naya – Mη), sedimentation constants ( medium-sedimentary I - M S) or diffusion coefficient ( average diffusion–M D).
The number average molecular weight is determined by the ratio:
Here N– number of macromolecules, xi– numerical fraction of macromolecules with molecular weight Mi. xi=Ni/Σ N i.
Experimentally n M measured by methods based on the colligative properties of solutions (depending on the number of particles). These methods include osmometry, cryoscopy, ebullioscopy and end group analysis.
The weight average molecular weight is determined by the ratio:
Here N– number of macromolecules, ωi– mass fraction of macromolecules with molecular weight Mi. ωi = Ni Mi /Σ N i Mi. Experimentally Mω is determined by the light scattering method. Magnitude Mω > n M for a polydisperse sample and Mω= Mn for a monodisperse sample. Values Mω are more sensitive to the presence of high molecular weight fractions in the sample, and n M– to the presence of low molecular weight fractions.
Attitude Mω/ n M=TO D is called indicator of polydispersity. If the sample is monodisperse, then TO D=1 (rare case). For most synthetic and natural polymers TO D>1, i.e. polymers are polydisperse, and TO D can vary widely (from 2 to 20). Polydispersity index values TO D are related to the mechanism of polymer formation. So, TO D=1.5 for the radical polymerization product at chain termination by recombination and TO D=2 – when the circuit breaks due to disproportionation. For polymers obtained by polycondensation, TO D=1 + X, where X is conversion. At X→1 (100%) TO D=2.
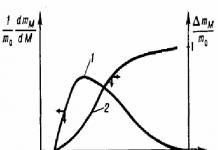
To characterize the polydispersity of polymers, in addition to the polydispersity indicator, curves are used molecular weight distribution(MMR). There are integral and differential MMR functions (Fig. 1), which can be numerical and mass. The integral MWD curve is the relationship between the MW and the integral mass (or numerical) fraction of the polymer fractions.
The differential MMD curve represents the dependence of MW on the mass [molecular mass distribution (MWD) (Fig. 2, curve 2)] or the numerical fraction of the fraction [molecular number distribution (MND) (Fig. 2, curve 1)]. The MMR and MMR curves do not coincide, since the numerical distribution is greatly influenced by low molecular weight fractions, and the mass distribution is influenced by high molecular weight fractions.
The abscissa of the center of gravity of the area bounded by the MMR curve is equal to Mω , and the abscissa of the center of gravity of the area bounded by the CDM curve is equal to n M(see Fig. 2). Distribution curves can have one (unimodal), two (bimodal) or several maxima (multimodal).
With the same average molecular mass, polymers can have different molecular mass distributions – narrow (in Fig. 3, curve 2) and wide (Fig. 3, curve 1).

Rice. 1. Curves of integral (2) and differential (1) mass MWD of the polymer.
Here Δ m / m0 is the relative integral fraction of fractions, and (1/ m0)(d m/d M) is the mass fraction of fractions.

Rice. 2. Differential curves of MCR (1) and MMR (2).

Rice. 3. MMD curves with different polydispersity and the same average MW value.
Polymer fractionation
Fractionation allows polymer samples to be separated into fractions with different MWs and is used to construct MWD curves. There are two types of fractionation: preparative And analytical. In preparative fractionation, individual fractions are isolated and their properties are studied. In analytical fractionation, a distribution curve is obtained without isolating individual fractions. Analytical fractionation methods include ultracentrifugation, turbodimetric titration, and gel permeation chromatography.
Preparative fractionation methods include fractional dissolution And fractional precipitation. These methods are based on the dependence of polymer solubility on MW - with increasing MW, the solubility of the polymer decreases. The fractional precipitation method involves the sequential precipitation from a polymer solution of fractions whose molecular weight decreases. Precipitation of fractions is caused in various ways:
By adding a precipitant to the polymer solution,
Evaporation of the solvent from the polymer solution,
A change in the temperature of the solution, which deteriorates the quality of the solvent.
The fractional dissolution method consists of sequential extraction of the polymer with a series of liquids with increasing dissolving ability. In this case, the isolated fractions have a consistently increasing molecular weight.
Construction of distribution curves by MM
As a result of fractionation, a number of fractions are isolated. For each fraction, the mass is determined and the MM is found. The experimental data are entered into the table.
Then the mass fraction of each fraction ωi is determined and then the integral mass fraction of the fractions is determined by summing all the fractions of the fractions, starting with the smallest fraction by MM. The calculated data is entered into the table.
Based on the table data, an integral MMR curve is constructed in coordinates Wi=f(MM) and the differential MMR curve in coordinates dWi/dMi=f(MM).
4. Isomerism of high molecular weight compounds. Features of isomerism of polymer materials, the concept of short-range and long-range order. Conformational and configurational isomerism of the elementary unit.
Local isomerism
This type of isomerism is characteristic of vinyl, vinylidene and diene polymers. So for a vinyl monomer molecule
The substituents on the C atoms (1) (head) and (2) (tail) are different and, therefore, two types of addition are possible

Head-to-head additions occur much less frequently than head-to-tail additions, primarily due to the steric hindrance that arises. For example, in polyvinylidene fluoride ( -CH 2 -CF 2 -) n the share of links connected by the “head-to-head” type is only 5-6%.
The formation of polyisoprene molecules can occur by adding monomer molecules at positions 1,4; 1.2; 3.4. In this case, isomers differing in configuration will be formed:

(In polybutadiene, due to the symmetrical structure of the monomer molecule, only the addition of 1,4 and 1,2 is possible). Depending on the nature of the catalyst and the polymerization conditions, the proportion of different configurations in the polymer chains can vary within wide limits. In polyisoprene, along with isomerism due to the method of addition at double bonds, there is also isomerism of addition of the “head-to-tail” and “head-to-head” type.
20.09.11 11:10
Deviations from the equilibrium state in short sections of the chain cause the manifestation of such a property of the polymer as flexibility in long sections.
Quantitative characteristics of the flexibility of a macromolecule can be the persistent length, statistical segment, root-mean-square distance between the ends of the chain, and the root-mean-square radius of gyration of the macromolecule.
RMS distance between chain ends . The conformation of the polymer coil is constantly changing and deviating from equilibrium. The distance between the ends of the chain changes. To find out what distance between the ends of the chain is most often realized, you need to take all the values obtained during measurements and divide by the number of measurements - i.e. find the average value (Fig. 8):
Rice. 8The distance between the ends of the chain (left) and the radius of gyration (right) in the representation of the freely articulated chain model
Knowing the length of the rigid segmentl Nand the number of such segments in the chainN, can be calculated
Rotation of rigid sections on hinges is free. For this model
Model with fixed bond angles b. It differs from the previous model in that the angle between two adjacent segments is fixed. Rotation around the axes remains free. In this case
Rotational isomer model . In this model, in addition to fixed bond angles, inhibited internal rotation appears, determined by the value of the torsion angle
For the perfect tangle, knowing
The average dimensions of a macromolecule can also be expressed in terms of the contour length of the chainL. The contour length of the chain is determined by the number of monomer units or SDRs that form the macromolecule. If you divide the chain into rigid sections of equal length, then O
From here we can write using the freely articulated model
This model is valid for assessing the thermodynamic flexibility of macromolecules of flexible-chain polymers (l N£ 100 Å or 10 nm).
From expressions (1), (2) one can find the value of the smallest rigid section of the chain (Kuhn segment) :
Based on expression (3), for the volume of the ball we can write
Gaussian distribution of distances between the ends of a chain
The typical conformation of a polymer coil has obvious similarities with the trajectory of a Brownian particle (Fig. 9b).
Vector r , which determines the distance between the ends of the chain, fluctuates greatly due to thermal motion. Consider the probability distribution of the vectorr between the ends of the chain ofNsegments for a freely jointed model of an ideal chain. Since each segment makes an independent contribution tor , then, by analogy with the trajectory of a Brownian particle, for the quantityr there will be a valid Gaussian distribution (therefore, an ideal tangle is often called a Gaussian tangle)
The flexibility of macromolecules is one of the most important characteristics of a polymer, determining its basic macroscopic properties. The flexibility of macromolecules is the ability of polymer chains to change their conformation as a result of intramolecular thermal movement of units ( thermodynamic flexibility ) or under the influence of external mechanical forces ( kinetic flexibility ). The flexibility of macromolecules is due to the fact that the monomer chain links rotate around single (s-) bonds during thermal motion or external force.
The concept of internal rotation of polymer macromolecules was first introduced by Kuhn, Mark and Guth. When the links rotate, the macromolecule changes its shape. Forms of macromolecules that transform into each other without breaking chemical bonds are called conformations . Many types of conformations of macromolecules are known: coil conformation, elongated rigid rod conformation, helix conformation, globule conformation (the most compact), folded (lamellar) conformation (usually in crystalline polymers), etc.
Let us consider one isolated polymer chain, the carbon atoms in which are connected only by s-bonds. Let us assume that the bond angles in such a chain are not fixed and rotation around the s-bonds is free. like this model the chain is called freely articulated (Fig. 3.4 (1). The links of a freely articulated chain can occupy arbitrary positions in space, regardless of the position of neighboring links. Such a chain can take on any conformation, i.e. it is extremely flexible.
In real polymer chains, bond angles have a very definite value, and the rotation of the links occurs without changing them (Fig. 3.4(2)). Therefore, in a real chain the links are not arranged arbitrarily: the position of each subsequent link turns out to be dependent on the position of the previous one. Even if we assume free rotation of the links, such a chain can take on fewer conformations than a freely jointed one. But it is capable of bending greatly due to the rotation of the links. Molecules in which fairly intense rotations of units around s-bonds are observed are called flexible chain , and polymers with weak rotations – rigid chain .Differentiate between thermodynamic and kinetic flexibility of macromolecules.
Thermodynamic flexibility (equilibrium flexibility) – the ability of macromolecules to change their conformations as a result of intramolecular thermal movement of units. Let's imagine a situation where one group of atoms of a polymer chain received a certain impulse as a result of the thermal movement of the links. An absolutely rigid molecule, under the influence of this impulse, would have to move entirely to a new position in space. In a flexible macromolecule, only a certain portion of it moves. Pulses of different sizes applied to different sections of the molecule will lead to the movement of sections of different sizes. The average statistical segment of a macromolecule, moving as a single whole in an elementary act of thermal motion, is called a segment (statistical segment of a macromolecule or statistical Kuhn element). The stiffer the chain, i.e. the larger the activation barrier of rotation DU, the larger the chain segment moves in the elementary act of thermal motion, i.e. the larger the segment. Thus, segment size can serve as a measure of the thermodynamic flexibility of macromolecules. A real molecule can be represented as consisting of N segments, each of length A:
where L is the length of the chain. For a freely articulated chain, A is the length of the link, and for an extremely rigid macromolecule, A = L.
The idea of a segment is not purely formal. It turned out that when measuring the molar mass of a polymer by any physicochemical method based on the colligative property (ebullioscopically, cryoscopically, osmometry, etc.), it turns out that it is less than the true molar mass measured, for example, by the viscometric method, and equal to the molar mass of the segment. This means that macromolecules in solutions do not behave as a single whole, but as a collection of small molecules with a length equal to the length of segment A.
Another estimate of thermodynamic flexibility can be the ratio of the root-mean-square dimensions of a macromolecule rolled into a statistical ball to the dimensions that the same molecule would have if the links were absolutely freely rotating.
Kinetic flexibility of macromolecules is the ability of macromolecules to change their conformations as a result of the influence of external mechanical forces. Depending on the ratio of the energy of these external influences and the potential barrier to rotation of the DU units, the polymer chain can unfold to one degree or another, i.e. exhibit kinetic flexibility.
By analogy with thermodynamic flexibility, the length of the kinetic segment can serve as a measure of kinetic flexibility . Indeed, if as a result of an external influence (for example, we pulled the ends of a polymer ribbon) one group of atoms of the polymer chain receives some impulse, then in the case of a flexible macromolecule only a certain section of it will move. Pulses of different sizes applied to different sections of the molecule will lead to the movement of sections of different sizes. A kinetic segment is an average segment of a macromolecule that moves as a single whole in an elementary act of external influence. The shorter the segment, the higher the kinetic flexibility of the macromolecule.
Most often, it is customary to consider as a measure of kinetic flexibility glass transition temperature – temperature range of transition of the polymer from the glassy to the highly elastic state. The higher the glass transition temperature of a polymer, the lower the kinetic flexibility of its macromolecules.
A universal and widespread method for determining Tst and Tt, as well as studying the deformation properties of polymers is the thermomechanical method. The method consists of measuring the dependence of deformation e on temperature T; a graphical representation of this dependence is called a thermomechanical curve (Fig. 3.5).
For amorphous linear polymers of high molecular weight, the thermomechanical curve has three sections corresponding to three physical states.
The first section (1) corresponds to the glassy state, which is characterized by small deformations, the second (2) to the highly elastic state with large reversible deformations. These deformations are superimposed (under prolonged load action) by flow deformation, which increases with increasing temperature. At sufficiently high temperatures, the movement of the chains as a whole is so facilitated that true polymer flow occurs. The polymer goes into a viscous flow state. This transition is accompanied by a sharp increase in deformation (section 3).
Temperatures T st and T t correspond to the average values of the temperature intervals at which a transition from one physical state of the polymer to another occurs.
Depending on the free volume, the polymer substance is in one of the physical states - glassy, highly elastic, viscous. Transitions from one state to another occur without the release or absorption of heat. The transition temperatures are called glass transition temperatures Tst and fluidity temperatures Tt.
Below Tst, intermolecular attraction excludes rotations around bonds, but it is not strong enough to exclude such rotations under the influence of an external load.
Polymers exhibit low stiffness and creep under load. Low stiffness is the result of reversible rotations around the bonds and distortion of the angles between the bonds under short-term load action. Under prolonged load action, deformation is essentially the result of irreversible rotations around the bonds and is called forced highly elastic deformation . Elongated molecules represent one of the types of nonequilibrium structures.
The supramolecular structures of thermoplastics below Tst depend on the processing and cooling conditions of the material and usually turn out to be nonequilibrium. The preservation of nonequilibrium structures in products is a characteristic feature of thermoplastics. Achieving uniaxial or biaxial orientation in polymer films is used to increase strength; oriented polymer fibers form an important group of high-strength fibers.
The transition of nonequilibrium structures to equilibrium ones is accompanied by warping and shrinkage of products during operation. To reduce this disadvantage, thermal stabilization is used - annealing − at temperatures exceeding maximum operating temperatures.
Supramolecular structures, in which tensile stresses from an external load act along valence bonds, are characterized by great rigidity. Similar structures are formed after very large drawing of polymer fibers. The elementary structural unit of a fiber, the fibril, contains alternating crystalline and amorphous sections. In amorphous areas, the molecules are extremely stretched. It is these areas that are loaded when the fiber is stretched, as a result of which the elastic modulus (E) turns out to be very large. For ordinary polyethylene with an amorphous-crystalline structure E = 120 ... 260 MPa, for polypropylene E = 160... 320 MPa. A copolymer of ethylene and propylene with a monomer ratio of 1:1 does not crystallize and at a temperature of 20-25°C is rubber, its modulus (at 300% tensile strength) is only 9-15 MPa. For polyethylene fiber, depending on the manufacturing technology E = 100 ... 170 GPa (for comparison, iron has E = 214 GPa).
The physical properties of substances depend on their chemical structure. The relationship between the physical properties of polymers and their structure is very complex, is “indirect” and manifests itself through the influence of the chemical structure on the flexibility of the macromolecule.
Flexibility is one of the most important characteristics of polymers, determining its basic microscopic properties: highly elastic, relaxation and thermomechanical properties of polymers, as well as the properties of their solutions. Flexibility characterizes the ability of macromolecules to change their shape under the influence of thermal movement of links or external mechanical influences.
Flexibility is due to the internal rotation of links or parts of macromolecules relative to each other.
The molecule of any substance is characterized by a certain spatial arrangement of atoms and the presence of certain bonds between them. This determines the chemical structure (structure, configuration) of the molecule. Let's consider the structure of two substances - ethane and ethylene (Fig. 6.1).
In an ethane molecule, carbon atoms are connected to hydrogen atoms and to each other by covalent bonds (formula" src="http://hi-edu.ru/e-books/xbook839/files/f122.gif" border="0" align="absmiddle" alt="-connection, second pair - example ">a and b) can be schematically represented by the formulas
example "> spatial isomerism (stereoisomerism), caused by different arrangements of substituents relative to the double bond. This type of spatial isomerism is called cis-trans isomerism.
The absence of stereoisomers in the ethane molecule is explained by the very rapid rotation of some groups of the molecule relative to others. This type of movement of one part of a molecule relative to another is called internal rotation.
In an ethane molecule, all hydrogen atoms are equivalent, and therefore it can be assumed that, regardless of their location in space, the potential energy of the molecule should be the same, i.e. that rotation is free. However, in reality, internal rotation in the ethane molecule is not free due to the interaction between neighboring atoms that are not chemically bonded to each other.
During thermal motion, the spatial arrangement of atoms continuously changes. Each position of the atoms corresponds to a certain value of the potential energy of the molecule, which is determined by the interactions between atoms, electrons, nuclei, etc.
When the group example">ethane is rotated around the line connecting the carbon atoms, the potential energy U changes.
Graphically, various extreme arrangements of atoms in a molecule can be represented in the form of projections of the molecule onto a horizontal plane (Fig. 6.2).
Let us assume that when the atoms in the ethane molecule are arranged as shown in Fig. 6.2, and, the potential energy of a molecule is equal to the formula" src="http://hi-edu.ru/e-books/xbook839/files/f125.gif" border="0" align="absmiddle" alt="(! LANG:should rotate relative to the other by 60° (Fig. 6.2, b)..gif" border="0" align="absmiddle" alt="at 60° the molecule returns to position again (Fig. 6.2, a).
From consideration of this example, it is obvious that the selection ">Fig. 6.2, b, because in this case repulsive forces appear between them, tending to transfer these atoms to the most energetically favorable, stable position, shown in Fig. 6.2, a. If we accept the potential energy of the molecule with the arrangement of atoms shown in Fig. 6.2, a, is equal to 0, then the potential energy corresponding to the model shown in Fig. 6.2, b, has a maximum value.
The energy required for a molecule to move from a position with a minimum value of potential energy to a position corresponding to its maximum value is called potential or rotational activation barrier.
For an ethane molecule, the potential barrier to rotation is relatively small, and at room temperature the kinetic energy is sufficient for free rotation. Therefore, ethane is actually a mixture of molecules, the atoms of which can occupy different spatial positions, i.e. is a mixture of rotary isomers. The transition from one position to another occurs 10 times per second, i.e. very quickly, so it is almost impossible to isolate ethane molecules with different arrangements of atoms. However, spectroscopic methods can prove the reality of their existence.
Increased values of the potential barrier to rotation are observed with an increase in the number of groups (example "> butane and butylene). The potential barriers to rotation around the C-O, C-S, C-Si bonds are relatively small.
If the potential barriers are sufficiently large, then even in the case of saturated compounds, molecules with a certain spatial structure can be identified.
Rotation of individual groups can also occur around a double bond, but for this it is necessary to break the formula" src="http://hi-edu.ru/e-books/xbook839/files/f122.gif" border="0" align=" absmiddle" alt="- connections. The links of such a chain are in thermal motion, i.e. one link can rotate relative to the adjacent link. Let us assume that the bond angles in such a chain are not fixed and the rotation around the selection is freely articulated.
It is obvious that the links of a freely articulated chain can occupy arbitrary positions in space, regardless of the position of neighboring links. Such a chain can take on any conformation, i.e. is extremely flexible (Fig. 6.3). In real chain polymer molecules, bond angles have a completely definite value, and the rotation of the links occurs without changing the bond angle (see Fig. 6.4). Therefore, in a real chain the links are not arranged arbitrarily, and the position of each subsequent link turns out to be dependent on the position of the previous one. Even if we assume the presence of free rotation, such a chain assumes a lower number of conformations than a freely jointed chain, but it is also capable of strong bending.
In real systems, polymer molecules are surrounded by other similar molecules and there is always an intermolecular interaction between them, which affects the degree of rotation inhibition. Since taking this interaction into account is very difficult, quantitative calculations are limited to taking into account only the intramolecular interaction of chemically unrelated atoms and groups of atoms of the same polymer molecule.
Rotations of links and their transition from an arrangement corresponding to one energy minimum to an arrangement corresponding to another energy minimum can occur only if the necessary energy reserve is available.
If a molecule has a reserve of energy less than a certain vibration of atoms relative to the position of the minimum energy, this is limited or inhibited rotation. The more intense these vibrations, the more flexible the molecule. Thus, a real polymer chain, due to intramolecular interaction, takes on fewer conformations than a freely jointed chain.
Polymers in which fairly intense torsional vibrations are observed are called flexible-chain, and polymers in which rotation of one part of the chain relative to the other is difficult are called rigid-chain.
There are two concepts of chain flexibility - TDG - thermodynamic flexibility and KG - kinetic flexibility of the polymer chain.
TDH determines the ability of a chain to undergo conformational transformations (i.e., without breaking chemical bonds under the influence of thermal motion).
This is equilibrium flexibility, which occurs in very dilute solutions in which the chains are in an isolated state.
TDG is characterized by several parameters. For example, stiffness parameter formula" src="http://hi-edu.ru/e-books/xbook839/files/f130.gif" border="0" align="absmiddle" alt="- parameter for assessing the flexibility of chain MMs, the flexibility of which is caused by rotation around valence bonds without deformation of valence angles. For many polymers this is not possible.
The most universal measure of flexibility is Kuhn segment size- a statistical element (or chain segment) of length A, the position of which does not depend on the position of neighboring elements or segments.
The real chain of a macromolecule can be divided into N independent statistical elements of segments A.
In a freely articulated chain, the position of each link does not depend on the position of the previous one, i.e. there is no correlation in the location of the links. In a real chain, the positions of the links in space are interconnected. However, with a very long chain length, there is also no correlation between the directions of location of links that are sufficiently distant from each other. If such links are connected by lines (Fig. 6.5), then the directions of these lines turn out to be independent. This means that a real chain consisting of n repeating links (the length of each link is l) can be divided into N independent statistical elements (segments or segments) of length A.
TD segment - in general not a segment of a real chain, but an equivalent value, reflecting the intensity of the oscillatory motion of the links or the flexibility of the chain.
For an extremely flexible chain A = l link..gif" border="0" align="absmiddle" alt="can be calculated by the number of segments M = N segments * A (molar mass of zvek).
In table 6.1. The values of the Kuhn segments of some polymer samples are given.
Table 6.1
Indicators characterizing TDG chains
Polymer |
Link |
A, nm |
Number |
Conformation |
| Polyethylene | CH 2 -CH 2 - |
Statistician clew |
||
| Polystyrene | CH 2 -SNS 6 H 5 - |
Statistician clew |
||
| PVC | CH 2 -CHCl- |
Statistician clew |
||
| Polymethyl methacrylate | CH 2 -C(CH 3)COOSH 3 - |
Statistician clew |
||
| EthylCl | Statistician clew |
|||
| Poly-n-benzamide | NH- C 6 H 5 -CO- |
Crankshaft |
||
| Biopolymers |
The nature of the substituents has little effect on TDH. The greatest rigidity is found in a polymer with closely spaced polar groups. Cyclic polyacetals (Cl and derivatives) belong to semi-rigid polymers.
Kinetic flexibility (KG) characterizes the rate of transition from one conformational position to another.
The rate of conformational transformations depends on the ratio of the potential rotation barrier and the energy of external influences (thermal, mechanical, etc.).
CG is characterized by the value kinetic segment, i.e. that part of the MM that responds to external influences as a whole.
The kinetic segment (as opposed to TDS) is a value that depends on T and the force of influence.
Let's consider the differences between TDG and CG (Fig. 6.6).
In polymers, due to intra- and intermolecular interactions, the dependence is the formula" src="http://hi-edu.ru/e-books/xbook839/files/f126.gif" border="0" align="absmiddle" alt="( !LANG:.gif" border="0" align="absmiddle" alt=". The transition energy difference is release ">thermodynamic flexibility. It determines the ability of the chain to bend under the influence of thermal motion.
Another characteristic of flexibility is the speed of transition of links from one position to another..gif" border="0" align="absmiddle" alt=", the slower the links turn and the less flexibility. The flexibility of macromolecules, determined by the value of release ">kinetic flexibility., the density of the spatial network, the size of substituents and temperature.
Carbon chain polymers
For carbon chain polymers least polar are limit hydrocarbons..gif" border="0" align="absmiddle" alt=", therefore polymers have great kinetic and thermodynamic flexibility.
Examples: PE, PP, PIB.
Especially low values formula" src="http://hi-edu.ru/e-books/xbook839/files/f134.gif" border="0" align="absmiddle" alt="Polybutadiene
Introduction into macromolecules of substituents containing polar groups leads to intra- and intermolecular interactions. In this case, the degree of polarity of the groups and the symmetry of their arrangement significantly influence.
Example:
The most polar groups formula" src="http://hi-edu.ru/e-books/xbook839/files/f136.gif" border="0" align="absmiddle" alt="
When introducing polar groups, there are three possible effects on flexibility:
Definition">Heterochain polymers
In heterochain polymers, rotation is possible around the C-O, C-N, Si-O, C-C bonds. Example values"> polyesters, polyamides, polyurethanes, silicone rubbers.
However, the flexibility of heterochain polymers may be limited by intermolecular interactions due to the formation of H-bonds (e.g. cellulose, polyamides). Cellulose (Cl) is one of the rigid chain polymers. It contains a large number of polar groups (-OH) and therefore cellulose is characterized by intra- and intermolecular interactions and high values of the molecular weight of the polymer
Increasing formula" src="http://hi-edu.ru/e-books/xbook839/files/f4.gif" border="0" align="absmiddle" alt="the number of conformations that a macromolecule can take increases and the flexibility of the chains increases, and even at large definitions the density of the spatial network
The more chemical bonds between macromolecules, the less flexibility of the chains, i.e. As the density of the spatial grid increases, flexibility decreases.
At the same time, with a small number of bonds (2-3% S), the flexibility of vulcanized rubber formula" src="http://hi-edu.ru/e-books/xbook839/files/f144.gif" border="0" align= "absmiddle" alt="Kg (ebonite - rubber with 30% S).
Effect of size and number of substituents
An increase in the number of polar and large substituents reduces the mobility of macromolecule units and reduces kinetic flexibility.
Example is decreased flexibility macromolecules butadiene copolymer and styrene with an increase in the content of bulky phenyl substituents in the chain.
PS at room temperature does not change conformations, i.e. is a rigid polymer.
If there are two substituents at one carbon atom in the polymer backbone (for example, the formula" src="http://hi-edu.ru/e-books/xbook839/files/f140.gif" border="0" align=" absmiddle" alt="in PMMA units), then the macromolecule becomes kinetically rigid.
Temperature
With increasing temperature, the kinetic energy of the macromolecule increases..gif" border="0" align="absmiddle" alt=", the links begin to rotate.
With increasing temperature, the value changes little, but the speed of rotation of the links increases and kinetic flexibility increases.
Example: PS at 100°C is a flexible polymer.
1. Features of the structure of polymers. Reasons for the flexibility of macromolecules. Education of associates
High molecular weight compounds are substances having a relative molecular weight of approximately 10,000 to several million. BMCs consisting of a large number of repeating identical units are called polymers.
Polymer molecules can be linear or branched. It is the linear forms of macromolecules that determine the typical properties of polymers: rubber-like elasticity, the ability to form strong films and threads, swell, and produce viscous solutions when dissolved.
Branching in macromolecules greatly affects their flexibility. Short and frequently spaced side chains increase the rigidity of the molecules. The flexibility of a macromolecule can be affected by solvent molecules or plasticizers.
The flexibility of the hydrocarbon chain is determined by the rotation of some sections of the chain relative to others around the same valence bond connecting neighboring carbon atoms. Since there are many such individual bonds in a macromolecule, the exceptional flexibility that hydrocarbon chains have becomes clear. Polymer molecules are not connected to each other and behave completely independently when they are in relatively dilute solutions. In concentrated solutions, when the probability of collision of molecules of a dissolved substance is high, macromolecules can interact and form associates.
Associates in dilute polymer solutions are not permanently existing formations and do not have a specific composition. Associates are also formed in NMS solutions due to the collision of two, three, four or more molecules. A feature of the formation of associates in IUD solutions is that long and flexible macromolecules can be included in separate sections in the composition of various associates.
2. General and distinctive properties of solutions of high molecular weight compounds (HMCs) and sols
BMC solutions are true solutions, thermodynamically stable and reversible, the particles contained in such solutions do not require a stabilizer, do not consist of many small molecules, as is the case with colloids, and represent individual molecules of relatively very large sizes. This is the difference between IUD solutions and solutions of low molecular weight compounds.
Solutions of IUDs in poor solvents contain molecules rolled into a compact ball with a clearly defined interfacial surface.
They represent a separate phase. Such IUD solutions can be classified as colloidal systems. Due to the large size of their molecules, BMC solutions have a number of properties of lyosols, which makes it possible to consider many problems simultaneously for both colloidal solutions and BMC solutions.
Unlike sols, IUD solutions are characterized by high viscosity, high stability, and swelling ability.
Sols can exist in a gaseous state (aerosols), but IUDs cannot, because the macromolecule will break.
3. Swelling. Stages of the swelling process. Factors influencing swelling. Swelling kinetics. Swelling degree. Limited and unlimited swelling. Swelling pressure. Concentration
The dissolution of high-molecular compounds with linear flexible molecules, in contrast to the dissolution of NMS, is accompanied by swelling.
When high molecular weight compounds swell, they absorb a low molecular weight solvent, significantly increase in mass, and at the same time change the mechanical properties without loss of homogeneity. The volume of the IUD can increase with swelling up to 1000 - 1500%.
At the first stage of swelling, solvation of macromolecules occurs as a result of diffusion of the solvent into a high-molecular substance. This stage is characterized by the release of heat and the ordering of the arrangement of solvent molecules around the macromolecule, as a result of which the entropy of the system in the first stage of dissolution usually even decreases. The main significance of this stage during dissolution is the destruction of the bonds between individual macromolecules, as a result of which they become free.
The second stage is swelling or dissolution, due to purely entropic reasons. At this stage, since solvation has already completed, the thermal effect is zero or has a negative value, and entropy increases sharply. The second stage of dissolution can be considered a purely osmotic process. Polymers swell most easily in a viscous and highly elastic state.
Factors affecting swelling include: thermodynamic activity of the solvent, temperature, physical state of the polymer, nature of the polymer and solvent. Typical swelling kinetic curves characterizing the solvent dependence are presented in the figure.
Kinetic curves for limited swelling are presented analytically:
![]() ,
,
where is the swelling rate constant; - degree of swelling upon reaching equilibrium and at time, respectively.
Having integrated, we obtain an equation for the kinetics of swelling, similar to the equation for the kinetics of Langmuir adsorption:
![]() ,
,
The swelling of a polymer in a liquid is characterized by the degree of swelling, calculated by the formula:
where is the polymer weight before and after swelling.
Swelling does not always end with dissolution. Very often, after reaching a certain degree of swelling, the process stops.
Reasons for limited swelling:
1. IUD and solvent have limited mixing ability. Therefore, as a result of swelling, two phases are formed in the system - a saturated solution of the polymer in the solvent and a saturated solution of the solvent in the polymer (gel, jelly). This limited swelling is of an equilibrium nature.
... "micelle" and "micellar solution". These terms were used by him to designate systems formed by non-stoichiometric compounds in an aqueous environment. The main contribution to the development of colloidal chemistry as a science belongs to T. Graham. As noted above, it was this scientist who came up with the idea of introducing the term “colloid”, derived from the Greek word “kolla”, meaning “glue”. While doing...





The distance traveled by a substance through the sorbent is directly proportional to the solubility of the substance in the solvent passed through. Makes it possible to completely separate the substances included in the mixture being separated. Colloidal chemistry Dispersed systems are systems consisting of many particles of one phase (dispersed), distributed in the volume of another phase - dispersive. Dispersive medium...





And much more, without which life itself is unthinkable. The entire human body is a world of particles that are in constant motion strictly according to certain rules that obey human physiology. Colloidal systems of organisms have a number of biological properties that characterize a particular colloidal state: 2.2 Colloidal system of cells. From the point of view of colloid-chemical physiology...
Metals with proteins, nucleic acids, lipids. Its practical application is associated with the synthesis of pharmacological drugs, the action of which is determined by complex metal ions. Bioorganic Chemistry Studies the relationship between the structures of organic substances and their biological functions, using mainly methods of organic and physical chemistry, as well as physics and mathematics. ...