Vlera më e vogël e derivatit sipas grafikut të funksionit. Derivati ​​i funksionit. Kuptimi gjeometrik i derivatit. Gjetja e intervaleve të rritjes dhe uljes së një funksioni

Derivati ​​i një funksioni është një nga temat më të vështira në kurrikulën shkollore. Jo çdo i diplomuar do t'i përgjigjet pyetjes se çfarë është një derivat.

Ky artikull shpjegon thjesht dhe qartë se çfarë është një derivat dhe pse është i nevojshëm.. Tani nuk do të përpiqemi për rigorozitet matematikor të paraqitjes. Gjëja më e rëndësishme është të kuptoni kuptimin.

Le të kujtojmë përkufizimin:

Derivati ​​është shpejtësia e ndryshimit të funksionit.

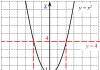
Figura tregon grafikët e tre funksioneve. Cili mendoni se rritet më shpejt?

Përgjigja është e qartë - e treta. Ajo ka shkallën më të lartë të ndryshimit, domethënë derivatin më të madh.

Këtu është një shembull tjetër.

Kostya, Grisha dhe Matvey morën punë në të njëjtën kohë. Le të shohim se si ndryshuan të ardhurat e tyre gjatë vitit:

Ju mund të shihni gjithçka në tabelë menjëherë, apo jo? Të ardhurat e Kostya janë dyfishuar në gjashtë muaj. Dhe të ardhurat e Grishës gjithashtu u rritën, por vetëm pak. Dhe të ardhurat e Mateut u ulën në zero. Kushtet e nisjes janë të njëjta, por shpejtësia e ndryshimit të funksionit, d.m.th. derivatore, - të ndryshme. Sa i përket Matvey-t, derivati ​​i të ardhurave të tij është përgjithësisht negativ.

Në mënyrë intuitive, ne mund të vlerësojmë lehtësisht shkallën e ndryshimit të një funksioni. Por si ta bëjmë?

Ajo që ne po shohim në të vërtetë është se sa pjerrësi rritet (ose poshtë) grafiku i funksionit. Me fjalë të tjera, sa shpejt ndryshon y me x. Natyrisht, i njëjti funksion në pika të ndryshme mund të ketë një vlerë të ndryshme të derivatit - domethënë, ai mund të ndryshojë më shpejt ose më ngadalë.

Derivati ​​i një funksioni shënohet me .

Le të tregojmë se si të gjejmë duke përdorur grafikun.

Vizatohet një grafik i disa funksioneve. Merrni një pikë mbi të me një abscissa. Vizatoni një tangjente me grafikun e funksionit në këtë pikë. Ne duam të vlerësojmë se sa pjerrësi rritet grafiku i funksionit. Një vlerë e dobishme për këtë është tangjenta e pjerrësisë së tangjentes.

Derivati ​​i një funksioni në një pikë është i barabartë me tangjenten e pjerrësisë së tangjentës së tërhequr në grafikun e funksionit në atë pikë.

Ju lutemi vini re - si kënd i prirjes së tangjentës, marrim këndin midis tangjentës dhe drejtimit pozitiv të boshtit.

Ndonjëherë studentët pyesin se sa është tangjentja me grafikun e një funksioni. Kjo është një vijë e drejtë që ka të vetmen pikë të përbashkët me grafikun në këtë seksion, për më tepër, siç tregohet në figurën tonë. Duket si një tangjente me një rreth.

Le të gjejmë. Kujtojmë se tangjentja e një këndi akut në një trekëndësh kënddrejtë është e barabartë me raportin e këmbës së kundërt me atë fqinj. Nga trekëndëshi:

Derivatin e gjetëm duke përdorur grafikun pa e ditur as formulën e funksionit. Detyra të tilla shpesh gjenden në provimin në matematikë nën numrin.

Ekziston një lidhje tjetër e rëndësishme. Kujtojmë se drejtëza jepet nga ekuacioni

Sasia në këtë ekuacion quhet pjerrësia e një vije të drejtë. Është e barabartë me tangjenten e këndit të prirjes së drejtëzës me boshtin.

.

Ne e kuptojmë atë

Le të kujtojmë këtë formulë. Ai shpreh kuptimin gjeometrik të derivatit.

Derivati ​​i një funksioni në një pikë është i barabartë me pjerrësinë e tangjentes së tërhequr në grafikun e funksionit në atë pikë.

Me fjalë të tjera, derivati ​​është i barabartë me tangjenten e pjerrësisë së tangjentes.

Ne kemi thënë tashmë se i njëjti funksion në pika të ndryshme mund të ketë një derivat të ndryshëm. Le të shohim se si derivati ​​lidhet me sjelljen e funksionit.

Le të vizatojmë një grafik të disa funksioneve. Lëreni këtë funksion të rritet në disa zona dhe të ulet në të tjera, dhe me ritme të ndryshme. Dhe le të ketë ky funksion pikë maksimale dhe minimale.

Në një moment, funksioni po rritet. Tangjentja e grafikut, e vizatuar në pikë, formon një kënd të mprehtë me drejtimin pozitiv të boshtit. Pra, derivati ​​është pozitiv në pikë.

Në këtë pikë, funksioni ynë është në rënie. Tangjentja në këtë pikë formon një kënd të mpirë me drejtimin pozitiv të boshtit. Meqenëse tangjentja e një këndi të mpirë është negative, derivati ​​në pikë është negativ.

Ja çfarë ndodh:

Nëse një funksion është në rritje, derivati ​​i tij është pozitiv.

Nëse zvogëlohet, derivati ​​i tij është negativ.

Dhe çfarë do të ndodhë në pikat maksimale dhe minimale? Shohim që në (pikën maksimale) dhe (pikën minimale) tangjentja është horizontale. Prandaj, tangjentja e pjerrësisë së tangjentës në këto pika është zero, dhe derivati ​​është gjithashtu zero.

Pika është pika maksimale. Në këtë pikë, rritja e funksionit zëvendësohet me një ulje. Rrjedhimisht, shenja e derivatit ndryshon në pikën nga "plus" në "minus".

Në pikën - pika minimale - derivati ​​është gjithashtu i barabartë me zero, por shenja e tij ndryshon nga "minus" në "plus".

Përfundim: me ndihmën e derivatit, mund të zbuloni gjithçka që na intereson për sjelljen e funksionit.

Nëse derivati ​​është pozitiv, atëherë funksioni është në rritje.

Nëse derivati ​​është negativ, atëherë funksioni është në rënie.

Në pikën maksimale, derivati ​​është zero dhe ndryshon shenjën nga plus në minus.

Në pikën minimale, derivati ​​është gjithashtu zero dhe ndryshon shenjën nga minus në plus.

Këto gjetje i shkruajmë në formën e një tabele:

Le të bëjmë dy sqarime të vogla. Një prej tyre do t'ju duhet kur zgjidhni problemet e provimit. Një tjetër - në vitin e parë, me një studim më serioz të funksioneve dhe derivateve.

Një rast është i mundur kur derivati ​​i një funksioni në një pikë është i barabartë me zero, por funksioni nuk ka as një maksimum dhe as një minimum në këtë pikë. Kjo e ashtuquajtura :

Në një pikë, tangjentja me grafikun është horizontale dhe derivati ​​është zero. Sidoqoftë, para pikës funksioni u rrit - dhe pas pikës ai vazhdon të rritet. Shenja e derivatit nuk ndryshon - ka mbetur pozitive siç ishte.

Ndodh gjithashtu që në pikën maksimale ose minimale, derivati ​​nuk ekziston. Në grafik, kjo korrespondon me një thyerje të mprehtë, kur është e pamundur të vizatoni një tangjente në një pikë të caktuar.

Por si të gjejmë derivatin nëse funksioni nuk jepet nga një grafik, por nga një formulë? Në këtë rast, ajo zbatohet

Në problemin B9, jepet një grafik i një funksioni ose derivati, nga i cili kërkohet të përcaktohet një nga madhësitë e mëposhtme:

1. Vlera e derivatit në një pikë x 0,
2. Pikat e larta ose të ulëta (pikat ekstreme),
3. Intervalet e funksioneve rritëse dhe zvogëluese (intervalet e monotonitetit).

Funksionet dhe derivatet e paraqitura në këtë problem janë gjithmonë të vazhdueshme, gjë që e thjeshton shumë zgjidhjen. Përkundër faktit se detyra i përket seksionit të analizës matematikore, ajo është mjaft në fuqinë edhe të studentëve më të dobët, pasi këtu nuk kërkohet njohuri e thellë teorike.

Për të gjetur vlerën e derivatit, pikave ekstreme dhe intervaleve të monotonitetit, ekzistojnë algoritme të thjeshta dhe universale - të gjitha do të diskutohen më poshtë.

Lexoni me kujdes gjendjen e problemit B9 në mënyrë që të mos bëni gabime të trashë: ndonjëherë hasen tekste mjaft voluminoze, por ka pak kushte të rëndësishme që ndikojnë në rrjedhën e zgjidhjes.

Llogaritja e vlerës së derivatit. Metoda me dy pika

Nëse problemit i jepet një grafik i funksionit f(x), tangjent me këtë grafik në një pikë x 0, dhe kërkohet të gjendet vlera e derivatit në këtë pikë, zbatohet algoritmi i mëposhtëm:

1. Gjeni dy pika "adekuate" në grafikun tangjentë: koordinatat e tyre duhet të jenë numër i plotë. Le t'i shënojmë këto pika si A (x 1 ; y 1) dhe B (x 2 ; y 2). Shkruani saktë koordinatat - kjo është pika kryesore e zgjidhjes dhe çdo gabim këtu çon në përgjigjen e gabuar.
2. Duke ditur koordinatat, është e lehtë të llogaritet rritja e argumentit Δx = x 2 − x 1 dhe rritja e funksionit Δy = y 2 − y 1 .
3. Së fundi, gjejmë vlerën e derivatit D = Δy/Δx. Me fjalë të tjera, ju duhet të ndani rritjen e funksionit me rritjen e argumentit - dhe kjo do të jetë përgjigja.

Edhe një herë, vërejmë: pikat A dhe B duhet të kërkohen saktësisht në tangjenten, dhe jo në grafikun e funksionit f(x), siç ndodh shpesh. Tangjentja do të përmbajë domosdoshmërisht të paktën dy pika të tilla, përndryshe problemi është formuluar gabimisht.

Merrni parasysh pikat A (−3; 2) dhe B (−1; 6) dhe gjeni rritjet:
Δx \u003d x 2 - x 1 \u003d -1 - (-3) \u003d 2; Δy \u003d y 2 - y 1 \u003d 6 - 2 \u003d 4.

Le të gjejmë vlerën e derivatit: D = Δy/Δx = 4/2 = 2.

Një detyrë. Figura tregon grafikun e funksionit y \u003d f (x) dhe tangjenten me të në pikën me abshisën x 0. Gjeni vlerën e derivatit të funksionit f(x) në pikën x 0 .

Merrni parasysh pikat A (0; 3) dhe B (3; 0), gjeni rritjet:
Δx \u003d x 2 - x 1 \u003d 3 - 0 \u003d 3; Δy \u003d y 2 - y 1 \u003d 0 - 3 \u003d -3.

Tani gjejmë vlerën e derivatit: D = Δy/Δx = −3/3 = −1.

Një detyrë. Figura tregon grafikun e funksionit y \u003d f (x) dhe tangjenten me të në pikën me abshisën x 0. Gjeni vlerën e derivatit të funksionit f(x) në pikën x 0 .

Merrni parasysh pikat A (0; 2) dhe B (5; 2) dhe gjeni rritjet:
Δx \u003d x 2 - x 1 \u003d 5 - 0 \u003d 5; Δy = y 2 - y 1 = 2 - 2 = 0.

Mbetet për të gjetur vlerën e derivatit: D = Δy/Δx = 0/5 = 0.

Nga shembulli i fundit, mund të formulojmë rregullin: nëse tangjentja është paralele me boshtin OX, derivati ​​i funksionit në pikën e kontaktit është i barabartë me zero. Në këtë rast, as nuk keni nevojë të llogaritni asgjë - thjesht shikoni grafikun.

Llogaritja e pikave të larta dhe të ulëta

Ndonjëherë në vend të një grafiku të një funksioni në problemin B9, jepet një grafik derivat dhe kërkohet të gjendet pika maksimale ose minimale e funksionit. Në këtë skenar, metoda me dy pika është e padobishme, por ekziston një algoritëm tjetër, edhe më i thjeshtë. Së pari, le të përcaktojmë terminologjinë:

1. Pika x 0 quhet pika maksimale e funksionit f(x) nëse në një afërsi të kësaj pike qëndron pabarazia e mëposhtme: f(x 0) ≥ f(x).
2. Pika x 0 quhet pika minimale e funksionit f(x) nëse në një fqinjësi të kësaj pike qëndron pabarazia e mëposhtme: f(x 0) ≤ f(x).

Për të gjetur pikët maksimale dhe minimale në grafikun e derivatit, mjafton të kryhen hapat e mëposhtëm:

1. Rivizatoni grafikun e derivatit, duke hequr të gjitha informacionet e panevojshme. Siç tregon praktika, të dhënat shtesë ndërhyjnë vetëm në zgjidhje. Prandaj, ne shënojmë zerot e derivatit në boshtin koordinativ - dhe kaq.
2. Gjeni shenjat e derivatit në intervalet midis zerove. Nëse për një pikë x 0 dihet se f'(x 0) ≠ 0, atëherë janë të mundshme vetëm dy opsione: f'(x 0) ≥ 0 ose f'(x 0) ≤ 0. Shenja e derivatit është lehtë për t'u përcaktuar nga vizatimi origjinal: nëse grafiku i derivatit shtrihet mbi boshtin OX, atëherë f'(x) ≥ 0. Në të kundërt, nëse grafiku i derivatit shtrihet nën boshtin OX, atëherë f'(x) ≤ 0.
3. Ne përsëri kontrollojmë zerot dhe shenjat e derivatit. Kur shenja ndryshon nga minus në plus, ka një pikë minimale. Në të kundërt, nëse shenja e derivatit ndryshon nga plus në minus, kjo është pika maksimale. Numërimi bëhet gjithmonë nga e majta në të djathtë.

Kjo skemë funksionon vetëm për funksione të vazhdueshme - nuk ka të tjerë në problemin B9.

Një detyrë. Figura tregon grafikun e derivatit të funksionit f(x) të përcaktuar në intervalin [−5; 5]. Gjeni pikën minimale të funksionit f(x) në këtë segment.

Le të heqim qafe informacionin e panevojshëm - do të lëmë vetëm kufijtë [−5; 5] dhe zerot e derivatit x = −3 dhe x = 2,5. Gjithashtu vini re shenjat:

Natyrisht, në pikën x = -3, shenja e derivatit ndryshon nga minus në plus. Kjo është pika minimale.

Një detyrë. Figura tregon grafikun e derivatit të funksionit f(x) të përcaktuar në intervalin [−3; 7]. Gjeni pikën maksimale të funksionit f(x) në këtë segment.

Le të rivizatojmë grafikun, duke lënë vetëm kufijtë [−3; 7] dhe zerot e derivatit x = −1,7 dhe x = 5. Vini re shenjat e derivatit në grafikun që rezulton. Ne kemi:

Natyrisht, në pikën x = 5, shenja e derivatit ndryshon nga plus në minus - kjo është pika maksimale.

Një detyrë. Figura tregon grafikun e derivatit të funksionit f(x) të përcaktuar në segmentin [−6; katër]. Gjeni numrin e pikave maksimale të funksionit f(x) që i përkasin intervalit [−4; 3].

Nga kushtet e problemit rezulton se mjafton të merret parasysh vetëm pjesa e grafikut e kufizuar nga segmenti [−4; 3]. Prandaj, ndërtojmë një grafik të ri, në të cilin shënojmë vetëm kufijtë [−4; 3] dhe zerot e derivatit brenda tij. Domethënë, pikat x = −3,5 dhe x = 2. Marrim:

Në këtë grafik ka vetëm një pikë maksimale x = 2. Është në të që shenja e derivatit ndryshon nga plus në minus.

Një shënim i vogël për pikat me koordinata jo të plota. Për shembull, në problemin e fundit është marrë parasysh pika x = -3.5, por me të njëjtin sukses mund të marrim x = -3.4. Nëse problemi është formuluar saktë, ndryshime të tilla nuk duhet të ndikojnë në përgjigjen, pasi pikat "pa vendbanim fiks" nuk përfshihen drejtpërdrejt në zgjidhjen e problemit. Sigurisht, me pikë të plota, një mashtrim i tillë nuk do të funksionojë.

Gjetja e intervaleve të rritjes dhe uljes së një funksioni

Në një problem të tillë, si pikat maksimale dhe minimale, propozohet të gjenden zona në të cilat funksioni vetë rritet ose zvogëlohet nga grafiku i derivatit. Së pari, le të përcaktojmë se çfarë janë ngjitëse dhe zbritëse:

1. Një funksion f(x) quhet në rritje në një segment nëse për çdo dy pika x 1 dhe x 2 nga ky segment pohimi është i vërtetë: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2). Me fjalë të tjera, sa më e madhe të jetë vlera e argumentit, aq më e madhe është vlera e funksionit.
2. Një funksion f(x) quhet zvogëlues në një segment nëse për çdo dy pika x 1 dhe x 2 nga ky segment pohimi është i vërtetë: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). ato. një vlerë më e madhe e argumentit korrespondon me një vlerë më të vogël të funksionit.

Ne formulojmë kushte të mjaftueshme për rritje dhe ulje:

1. Që një funksion i vazhdueshëm f(x) të rritet në segmentin , mjafton që derivati ​​i tij brenda segmentit të jetë pozitiv, d.m.th. f'(x) ≥ 0.
2. Që një funksion i vazhdueshëm f(x) të zvogëlohet në segmentin , mjafton që derivati ​​i tij brenda segmentit të jetë negativ, d.m.th. f'(x) ≤ 0.

Ne i pranojmë këto pohime pa prova. Kështu, marrim një skemë për gjetjen e intervaleve të rritjes dhe uljes, e cila në shumë mënyra është e ngjashme me algoritmin për llogaritjen e pikave ekstreme:

1. Hiq të gjitha informacionet e tepërta. Në grafikun origjinal të derivatit, ne jemi të interesuar kryesisht për zerot e funksionit, kështu që i lëmë vetëm ato.
2. Shënoni shenjat e derivatit në intervalet ndërmjet zerove. Ku f'(x) ≥ 0, funksioni rritet, dhe ku f'(x) ≤ 0, zvogëlohet. Nëse detyra ka kufizime në ndryshoren x, ne i shënojmë ato në grafikun e ri.
3. Tani që e dimë sjelljen e funksionit dhe kufizimin, mbetet të llogarisim vlerën e kërkuar në problem.

Një detyrë. Figura tregon grafikun e derivatit të funksionit f(x) të përcaktuar në intervalin [−3; 7.5]. Gjeni intervalet e funksionit zvogëlues f(x). Në përgjigjen tuaj, shkruani shumën e numrave të plotë të përfshirë në këto intervale.

Si zakonisht, ne rivizatojmë grafikun dhe shënojmë kufijtë [−3; 7.5], si dhe zerot e derivatit x = −1.5 dhe x = 5.3. Pastaj shënojmë shenjat e derivatit. Ne kemi:

Meqenëse derivati ​​është negativ në intervalin (− 1.5), ky është intervali i funksionit në rënie. Mbetet për të mbledhur të gjithë numrat e plotë që janë brenda këtij intervali:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Një detyrë. Figura tregon grafikun e derivatit të funksionit f(x) të përcaktuar në segmentin [−10; katër]. Gjeni intervalet e funksionit rritës f(x). Në përgjigjen tuaj, shkruani gjatësinë e më të madhit prej tyre.

Le të heqim qafe informacionin e tepërt. Ne lëmë vetëm kufijtë [−10; 4] dhe zero të derivatit, që kësaj radhe rezultuan katër: x = −8, x = −6, x = −3 dhe x = 2. Vëreni shenjat e derivatit dhe merrni figurën e mëposhtme:

Ne jemi të interesuar për intervalet e rritjes së funksionit, d.m.th. ku f'(x) ≥ 0. Ekzistojnë dy intervale të tilla në grafik: (−8; −6) dhe (−3; 2). Le të llogarisim gjatësinë e tyre:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.

Meqenëse kërkohet gjetja e gjatësisë së intervalit më të madh, si përgjigje shkruajmë vlerën l 2 = 5.

Sergei Nikiforov

Nëse derivati ​​i një funksioni është me shenjë konstante në një interval, dhe vetë funksioni është i vazhdueshëm në kufijtë e tij, atëherë pikat kufitare i bashkëngjiten intervaleve në rritje dhe në ulje, gjë që korrespondon plotësisht me përcaktimin e funksioneve në rritje dhe në zvogëlim.

Farit Yamaev 26.10.2016 18:50

Përshëndetje. Si (në çfarë baze) mund të argumentohet se në pikën ku derivati ​​është i barabartë me zero, funksioni rritet. Jep arsye. Përndryshe, është vetëm teka e dikujt. Me çfarë teoreme? Dhe gjithashtu prova. Faleminderit.

Mbështetje

Vlera e derivatit në një pikë nuk lidhet drejtpërdrejt me rritjen e funksionit në interval. Konsideroni, për shembull, funksionet - ato të gjitha rriten në segment

Vladlen Pisarev 02.11.2016 22:21

Nëse një funksion është në rritje në intervalin (a;b) dhe është i përcaktuar dhe i vazhdueshëm në pikat a dhe b, atëherë ai rritet në segmentin . ato. pika x=2 përfshihet në intervalin e dhënë.

Edhe pse, si rregull, rritja dhe ulja konsiderohet jo në një segment, por në një interval.

Por pikërisht në pikën x=2, funksioni ka një minimum lokal. Dhe si t'u shpjegojmë fëmijëve se kur kërkojnë pikë rritjeje (uljeje), atëherë nuk i numërojmë pikët e ekstremit lokal, por ato hyjnë në intervalet e rritjes (uljes).

Duke marrë parasysh që pjesa e parë e provimit është për "grupin e mesëm të kopshtit", atëherë nuanca të tilla ndoshta janë të tepërta.

Më vete, shumë faleminderit për "Unë do të zgjidh provimin" për të gjithë punonjësit - një udhëzues i shkëlqyeshëm.

Sergei Nikiforov

Një shpjegim i thjeshtë mund të merret nëse nisemi nga përkufizimi i një funksioni në rritje/zvogëlim. Më lejoni t'ju kujtoj se tingëllon kështu: një funksion quhet rritje/zvogëlim në interval nëse argumenti më i madh i funksionit korrespondon me një vlerë më të madhe/më të vogël të funksionit. Një përkufizim i tillë nuk e përdor në asnjë mënyrë konceptin e një derivati, kështu që nuk mund të lindin pyetje në lidhje me pikat ku zhduket derivati.

Irina Ishmakova 20.11.2017 11:46

Mirembrema. Këtu në komente shoh bindjet se duhet të përfshihen kufijtë. Le të themi se jam dakord me këtë. Por shikoni, ju lutem, zgjidhjen tuaj për problemin 7089. Atje, kur specifikoni intervalet e rritjes, kufijtë nuk përfshihen. Dhe kjo ndikon në reagimin. ato. zgjidhjet e detyrave 6429 dhe 7089 kundërshtojnë njëra-tjetrën. Ju lutemi sqaroni këtë situatë.

Aleksandër Ivanov

Detyrat 6429 dhe 7089 kanë pyetje krejtësisht të ndryshme.

Në njërën, ka intervale rritjeje, dhe në tjetrën, ka intervale me një derivat pozitiv.

Nuk ka asnjë kontradiktë.

Ekstremat përfshihen në intervalet e rritjes dhe uljes, por pikat në të cilat derivati ​​është i barabartë me zero nuk hyjnë në intervalet në të cilat derivati ​​është pozitiv.

A Z 28.01.2019 19:09

Kolegë, ekziston një koncept i rritjes në një pikë

(shih Fichtenholtz për shembull)

dhe kuptimi juaj i rritjes në pikën x=2 është në kundërshtim me përkufizimin klasik.

Rritja dhe zvogëlimi është një proces dhe unë do të doja t'i përmbahesha këtij parimi.

Në çdo interval që përmban pikën x=2, funksioni nuk rritet. Prandaj, përfshirja e pikës së dhënë x=2 është një proces i veçantë.

Zakonisht, për të shmangur konfuzionin, përfshirja e skajeve të intervaleve thuhet veçmas.

Aleksandër Ivanov

Funksioni y=f(x) quhet në rritje në një interval nëse vlera më e madhe e argumentit nga ky interval korrespondon me vlerën më të madhe të funksionit.

Në pikën x = 2, funksioni është i diferencueshëm, dhe në intervalin (2; 6) derivati ​​është pozitiv, që do të thotë se në intervalin )