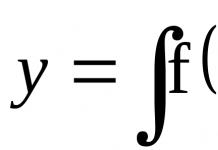Per completare il test n. 3

Indicazioni

(argomenti 12-16)

Argomento 12. Equazioni differenziali del 1° ordine.

Piskunov, cap. VIII, § 1-8, es. 1-68

Danko, parte II, cap. IV, §1

12.1 Definizione di equazione differenziale del primo ordine.

1.Definizione. Uguaglianza relativa alla variabile indipendente X, funzione A e le derivate (o differenziali) di questa funzione sono chiamate equazioni differenziali del primo ordine (DY1) quelli.

F(x,y,y")=0 O y"=f (x,y)

Risolvere un'equazione differenziale del primo ordine- significa trovare una funzione sconosciuta sì.

2.Soluzione generale di un'equazione differenziale del primo ordine è chiamata funzione y=j(x,c), Dove C- una costante che, sostituita in un'equazione differenziale del primo ordine, la trasforma in un'identità. In superficie XOY decisione comune y=j(x,c) esprime una famiglia di curve integrali.

3. Ogni decisione y= j (x,С 0) ottenuto dalla soluzione generale ad un valore specifico C=C0 chiamato soluzione privata Equazione differenziale del primo ordine.

4. Il problema di trovare una particolare soluzione ad un'equazione differenziale del primo ordine che soddisfi la condizione iniziale

O o

5. -DE 1 con variabili separabili.

6. - ODE 1 – equazione differenziale omogenea del 1° ordine o , dove , sono funzioni omogenee di una dimensione. Viene utilizzata la sostituzione

7. , dove . DE 1, ridotto ad omogeneo per sostituzione

Dov'è il punto di intersezione delle linee

Se , allora viene utilizzata la sostituzione

8. , dove - è detta equazione differenziale totale.

Dov'è il differenziale totale della funzione

Risolvere questa equazione significa trovare la funzione E.

9. - telecomando lineare 1 (LDU 1)

Se , allora l'equazione non è omogenea,

Se , allora l'equazione è omogenea.

LDU 1 è integrato:

1) Metodo Bernoulli (utilizzando la sostituzione y = ev, Dove tu E v-funzioni ancora sconosciute)

2) Utilizzando il metodo di Lagrange, variando una costante arbitraria.

10. , dove M- numero, m¹0, m¹1- Equazione differenziale di Bernoulli, risolta mediante sostituzione y= uv, o il metodo di Lagrange (cfr. paragrafo 9).

12.2. Esempi di risoluzione dei problemi.

Compito 1. Trovare una soluzione particolare di DE 1 che soddisfi la condizione iniziale.

Soluzione: Questa è un'equazione con variabili separabili.

Perché , allora l'equazione assumerà la forma:

Oppure - dopo aver separato le variabili.

Integrando entrambi i membri dell'ultima equazione, otteniamo:

Oppure - soluzione generale

Utilizzando la condizione iniziale, troviamo . Dalla soluzione generale si estrae quindi una soluzione particolare:

Compito 2.

Soluzione: Questa equazione è omogenea, poiché i coefficienti per dx E dy sono funzioni omogenee della stessa dimensione (la seconda) rispetto alle variabili X E sì. Applicazione della sostituzione y=xt, Dove T- qualche funzione di argomento X. Se y=xt, quindi il differenziale dy = d(xt) = tdx+ xdt, e questa equazione assumerà la forma:

2xxtdt+(x²t²-x²) (tdx+xdt)= 0

Ridotto da x², avrà:

2tdx+(t²-1) (tdx+xdt)=0

2tdx+(t²-1) tdx+x (t²-1)dt=0

t(2+t²-1) dx+x (t²-1)dt=0

t(1+t²)dx= x(1-t²)dt;.

Abbiamo ottenuto un'equazione a variabili separate rispetto a X E T. Integrando, troviamo la soluzione generale di questa equazione:

Potenziando, troviamo , o x(1+t²)=Ct. Dalla sostituzione introdotta ne consegue che . Pertanto, o x²+y²=Cyè la soluzione generale di questa equazione.

Compito 3. Trova la soluzione generale dell'equazione y"-y tg x=2 xsec x.

Soluzione: Questa equazione è lineare, poiché contiene la funzione desiderata y e la sua derivata sì" di primo grado e non contiene loro opere.

Applicazione della sostituzione y=uv, Dove tu E v–alcune funzioni di argomento sconosciute X. Se y=uv, Quello y"= (uv)"= u"v+uv" e questa equazione assumerà la forma: u"v+uv"-uvtg x= 2x sec x,

v(u"-utg x)+ uv"= 2xsec x. (1)

Poiché la funzione richiesta sì viene presentato come il prodotto di altre due funzioni sconosciute, allora una di esse può essere scelta arbitrariamente. Selezioniamo una funzione tu in modo che l'espressione tra parentesi a sinistra della disuguaglianza (1) diventi zero, ovvero scegliamo la funzione tu in modo che ci sia uguaglianza

u"-utgx= 0 (2)

Con questa scelta della funzione u, l'equazione (1) assume la forma

uv"= 2x secondo x. (3)

L'equazione (2) è un'equazione separabile rispetto a u e x. Risolviamo questa equazione:

ln u= -ln cos x, O

(Affinché si verifichi l'uguaglianza (2), è sufficiente trovare una soluzione particolare che soddisfi questa equazione. Pertanto, per semplicità, integrando questa equazione, troviamo quella soluzione particolare che corrisponde al valore della costante arbitraria C = 0 .) Sostituendo in (3) l'espressione trovata per tu, noi abbiamo:

secxv"= 2xsecx; v"= 2X; dv= 2xdx. Integrando, otteniamo v=x²+C. Poi y=secx(x²+C)è la soluzione generale di questa equazione.

12.3.Domande per l'autocontrollo.

1. Quale equazione si chiama differenziale?

2. Come viene determinato l'ordine di un'equazione? Esempi.

3. Cosa significa decidere?

4. Quale funzione è chiamata soluzione?

5. Quale soluzione si chiama generale, particolare?

6. Come trovare una soluzione particolare in base alle condizioni iniziali? Annota un piano di operazioni eseguite durante la risoluzione di un esempio sì"- 2x= 0 alle condizioni iniziali sì(-2)= 4.

7. Formulare il significato geometrico delle soluzioni generali e particolari.

L'equazione più semplice 1 è un'equazione della forma, come noto dal corso di calcolo integrale, la funzione sì si trova per integrazione

Definizione. Un'equazione della forma è chiamata equazione differenziale con variabili separate. Può essere scritto nella forma

Integriamo entrambi i membri dell'equazione e otteniamo il cosiddetto integrale generale (o soluzione generale).

Esempio.

Soluzione. Scriviamo l'equazione nella forma
Integriamo entrambi i lati dell'equazione:

(integrale generale di un'equazione differenziale).

Definizione. Un'equazione della forma è chiamata equazione con variabili separabili, se le funzioni possono essere rappresentate come prodotto di funzioni

cioè l'equazione ha la forma

Per risolvere tale equazione differenziale, dobbiamo ridurla alla forma di un'equazione differenziale con variabili separate, per la quale dividiamo l'equazione nel prodotto
Infatti, dividendo tutti i termini dell'equazione per il prodotto
,

–equazione differenziale a variabili separate.

Per risolverlo è sufficiente integrare termine per termine

Quando risolvi un'equazione differenziale con variabili separabili, puoi essere guidato da quanto segue algoritmo (regola) per separare le variabili.

Primo passo. Se un'equazione differenziale contiene una derivata , dovrebbe essere scritto come rapporto tra differenziali:

Secondo passo. Moltiplicare l'equazione per
, quindi raggruppiamo i termini contenenti il ​​differenziale della funzione e il differenziale della variabile indipendente
.

Terzo passo. Espressioni ottenute con
, rappresentatelo come un prodotto di due fattori, ciascuno dei quali contiene una sola variabile (
). Se dopo ciò l'equazione diventa visibile, dividendola per il prodotto
, otteniamo un'equazione differenziale con variabili separate.

Quarto passo. Integrando l'equazione termine per termine, otteniamo una soluzione generale dell'equazione originale (o del suo integrale generale).

Considera le equazioni

№ 2.

№ 3.

L'equazione differenziale n. 1 è un'equazione differenziale separabile, per definizione. Dividi l'equazione per il prodotto
Otteniamo l'equazione

Integrando, otteniamo

O

L'ultima relazione è l'integrale generale di questa equazione differenziale.

Nell'equazione differenziale n. 2 sostituiamo
moltiplicato per
, noi abbiamo

Soluzione generale di un'equazione differenziale.

L'equazione differenziale n. 3 non è un'equazione a variabili separabili, perché, avendola scritta nella forma

O
,

vediamo che l'espressione
sotto forma di prodotto di due fattori (uno –

soltanto Con sì, l'altro – solo con X) è impossibile da immaginare. Si noti che a volte è necessario eseguire trasformazioni algebriche per vedere che una data equazione differenziale è a variabili separabili.

Esempio n.4. Data un'equazione, trasforma l'equazione spostando il divisore comune a sinistra
Dividi i lati sinistro e destro dell'equazione per il prodotto
noi abbiamo

Integriamo entrambi i lati dell'equazione:

Dove
è l'integrale generale di questa equazione. (UN)

Si noti che se la costante di integrazione è scritta nella forma
, allora l'integrale generale di questa equazione può avere una forma diversa:

O
– integrale generale. (B)

Pertanto, l'integrale generale della stessa equazione differenziale può avere forme diverse. In ogni caso, è importante dimostrare che l'integrale generale risultante soddisfa l'equazione differenziale data. Per fare ciò, è necessario differenziare per X entrambi i lati dell'uguaglianza che definiscono l'integrale generale, tenendo conto di ciò sì c'è una funzione da X. Dopo l'eliminazione Con otteniamo equazioni differenziali identiche (originale). Se l'integrale generale
, (visualizzazione ( UN)), Quello

Se l'integrale generale
(tipo (b)), allora

Otteniamo la stessa equazione del caso precedente (a).

Consideriamo ora semplici ed importanti classi di equazioni del primo ordine riducibili ad equazioni a variabili separabili.

Equazione differenzialeè una relazione che assomiglia F(x 1 ,x 2 ,x 3 ,..,y,y′,y′′,...y (n)) = 0, e che mette in relazione le variabili indipendenti x1,x2,x3,... funzione y di queste variabili indipendenti e delle sue derivate fino a N-esimo ordine. Inoltre, la funzione Fè definito e differenziato un numero sufficiente di volte in una certa gamma di cambiamenti nelle sue argomentazioni.

Equazioni differenziali ordinarie sono equazioni differenziali contenenti una sola variabile indipendente.

Equazioni alle derivate parziali- queste sono equazioni differenziali che contengono 2 o più variabili indipendenti.

Un'equazione differenziale del primo ordine nel caso generale contiene:

1) variabile indipendente X;

2) variabile dipendente sì(funzione);

3) la derivata prima della funzione: sì’ .

In alcune equazioni del primo ordine potrebbe esserci no X o/e sì, ma questo non è essenziale: è importante che le equazioni differenziali abbiano la derivata 1a sì’ , e non c'erano derivate di ordine superiore - sì’’ , sì’’’ e così via.

Equazione differenziale- un'equazione che collega il valore della derivata di una funzione con la funzione stessa, i valori della variabile indipendente e i numeri (parametri). L'ordine delle derivate incluse nell'equazione può essere diverso (formalmente non è limitato). Derivate, funzioni, variabili indipendenti e parametri possono essere inclusi nell'equazione in varie combinazioni, oppure tutti tranne la prima derivata possono essere completamente assenti. Non tutte le equazioni che contengono derivate di una funzione sconosciuta risultano essere un'equazione differenziale. Per esempio, non è un'equazione differenziale.

Un'equazione differenziale di ordine superiore al 1° può essere trasformata in un sistema di equazioni del 1° ordine in cui il numero di equazioni è uguale all'ordine dell'equazione iniziale.

Classificazione delle equazioni differenziali.

Ordine delle equazioni differenzialiè l'ordine della derivata più alta in esso inclusa.

Grado dell'equazione differenzialeè l'esponente a cui viene elevata la derivata di ordine massimo.

Per esempio, equazione di 1° ordine di 2° grado:

Per esempio, equazione del 4° ordine di 1° grado:

A volte le equazioni differenziali sono scritte come (include i differenziali):

(X 2 - 3 xy 2 ) dx + (xy 2 - 3 X 2 sì) dy = 0;

In questo caso, le variabili X E sì devono essere considerati uguali. Se necessario, tale equazione può essere ridotta ad una forma che contenga esplicitamente la derivata sì". Dividi per dx:

Poiché e , significa che l'equazione assume una forma che contiene una derivata del primo ordine.

Equazioni differenziali del primo ordine

Caratteristiche delle equazioni differenziali del primo ordine

Quando si risolvono equazioni del primo ordine, la funzione y e la variabile x dovrebbero essere considerate uguali. Cioè, la soluzione può essere nella forma e nella forma .

Equazioni differenziali del primo ordine risolte rispetto alla derivata

Equazioni separabili

Equazioni che si riducono ad equazioni separabili

Equazioni omogenee

Equazioni che si riducono a omogenee

Equazioni omogenee generalizzate

Equazioni differenziali lineari

• Lineare in y
• Lineare in f(y)
• Lineare in x
• Lineare in f(x)

Le equazioni di Bernoulli

Equazioni di Riccati

Equazioni di Jacobi

Equazioni ai differenziali totali

dato che

Fattore integrativo

Se un'equazione differenziale del primo ordine non può essere ridotta a nessuno dei tipi elencati, dovresti provare a trovare un fattore di integrazione per ridurla a un'equazione differenziale totale.

Equazioni non risolte per la derivata y′

Equazioni risolvibili rispetto alla derivata y′

Per prima cosa devi provare a risolvere l'equazione rispetto alla derivata y′. Se possibile, l'equazione può essere ridotta a uno dei tipi sopra elencati.

Equazioni che possono essere fattorizzate

Equazioni che non contengono x e y

Equazioni che non contengono x o y

O

Equazioni risolte per y

Equazioni di Clairaut

Equazioni di Lagrange

Equazioni che portano all'equazione di Bernoulli

Equazioni differenziali di ordine superiore

Equazioni differenziali che consentono la riduzione dell'ordine

Equazioni risolte mediante integrazione diretta

Equazioni che non contengono y

Equazioni che non contengono x

Equazioni omogenee rispetto a y, y′, y′′, ...

Equazioni lineari disomogenee con una parte speciale disomogenea

,
dove sono i polinomi di gradi e .

Equazioni di Eulero

Riferimenti:
V.V. Stepanov, Corso di equazioni differenziali, "LKI", 2015.
N.M. Gunter, R.O. Kuzmin, Raccolta di problemi di matematica superiore, “Lan”, 2003.

Equazioni differenziali del primo ordine. Esempi di soluzioni.
Equazioni differenziali a variabili separabili

Equazioni differenziali (DE). Queste due parole di solito terrorizzano la persona media. Le equazioni differenziali sembrano essere qualcosa di proibitivo e difficile da padroneggiare per molti studenti. Uuuuuu... equazioni differenziali, come posso sopravvivere a tutto questo?!

Questa opinione e questo atteggiamento sono fondamentalmente sbagliati, perché in effetti EQUAZIONI DIFFERENZIALI: È SEMPLICE E ANCHE DIVERTENTE. Cosa devi sapere ed essere in grado di fare per imparare a risolvere le equazioni differenziali? Per studiare con successo le diffusioni, devi essere bravo a integrare e differenziare. Meglio si studiano gli argomenti Derivata di una funzione di una variabile E Integrale indefinito, tanto più facile sarà comprendere le equazioni differenziali. Dirò di più, se hai capacità di integrazione più o meno decenti, allora l'argomento è quasi stato padroneggiato! Più integrali di vario tipo riesci a risolvere, meglio è. Perché? Dovrai integrare molto. E differenziare. Anche altamente raccomandato imparare a trovare.

Nel 95% dei casi, le prove contengono 3 tipi di equazioni differenziali del primo ordine: equazioni separabili che vedremo in questa lezione; equazioni omogenee E equazioni lineari non omogenee. Per chi inizia a studiare i diffusori, ti consiglio di leggere le lezioni esattamente in questo ordine e, dopo aver studiato i primi due articoli, non farà male consolidare le tue capacità in un workshop aggiuntivo - equazioni che si riducono a omogenee.

Esistono tipi ancora più rari di equazioni differenziali: equazioni differenziali totali, equazioni di Bernoulli e alcune altre. I più importanti degli ultimi due tipi sono le equazioni alle derivate totali, poiché oltre a questa equazione differenziale sto considerando nuovo materiale: integrazione parziale.

Se ti restano solo un giorno o due, Quello per una preparazione ultraveloce C'è corso lampo in formato pdf.

Quindi, i punti di riferimento sono fissati: andiamo:

Per prima cosa ricordiamo le solite equazioni algebriche. Contengono variabili e numeri. L'esempio più semplice: . Cosa significa risolvere un'equazione ordinaria? Questo significa trovare insieme di numeri, che soddisfano questa equazione. È facile notare che l'equazione dei bambini ha un'unica radice: . Solo per divertimento, controlliamo e sostituiamo la radice trovata nella nostra equazione:

– si ottiene l’uguaglianza corretta, il che significa che la soluzione è stata trovata correttamente.

I diffusori sono progettati più o meno allo stesso modo!

Equazione differenziale primo ordine generalmente contiene:
1) variabile indipendente;
2) variabile dipendente (funzione);
3) la derivata prima della funzione: .

In alcune equazioni del primo ordine potrebbero non esserci "x" e/o "y", ma questo non è significativo - importante per andare alla sala di controllo era derivata prima e non aveva derivati ​​di ordine superiore – , ecc.

Cosa significa ? Risolvere un'equazione differenziale significa trovare insieme di tutte le funzioni, che soddisfano questa equazione. Un tale insieme di funzioni ha spesso la forma (– una costante arbitraria), che viene chiamata soluzione generale dell'equazione differenziale.

Esempio 1

Risolvere l'equazione differenziale

Munizioni complete. Da dove cominciare soluzione?

Prima di tutto, devi riscrivere la derivata in una forma leggermente diversa. Ricordiamo la designazione ingombrante, che probabilmente a molti di voi è sembrata ridicola e inutile. Questo è ciò che governa nei diffusori!

Nel secondo passaggio, vediamo se è possibile variabili separate? Cosa significa separare le variabili? In parole povere, sul lato sinistro dobbiamo andarcene solo "greci", UN dal lato giusto organizzare solo "X". La divisione delle variabili viene effettuata utilizzando manipolazioni “scolastiche”: mettendole tra parentesi, trasferendo termini da parte a parte con cambio di segno, trasferendo fattori da parte a parte secondo la regola della proporzione, ecc.

I differenziali e sono moltiplicatori completi e partecipanti attivi alle ostilità. Nell’esempio in esame, le variabili possono essere facilmente separate lanciando i fattori secondo la regola delle proporzioni:

Le variabili sono separate. Sul lato sinistro ci sono solo le “Y”, sul lato destro solo le “X”.

Prossima fase - integrazione di equazioni differenziali. È semplice, mettiamo gli integrali su entrambi i membri:

Naturalmente dobbiamo prendere gli integrali. In questo caso sono tabellari:

Come ricordiamo, a qualsiasi antiderivativa viene assegnata una costante. Qui ci sono due integrali, ma è sufficiente scrivere la costante una volta (poiché costante + costante è ancora uguale a un'altra costante). Nella maggior parte dei casi è posizionato sul lato destro.

A rigor di termini, dopo aver preso gli integrali, l'equazione differenziale è considerata risolta. L'unica cosa è che la nostra “y” non è espressa tramite “x”, cioè viene presentata la soluzione in modo implicito modulo. La soluzione di un'equazione differenziale in forma implicita si chiama integrale generale dell'equazione differenziale. Cioè, questo è un integrale generale.

La risposta in questa forma è abbastanza accettabile, ma esiste un'opzione migliore? Proviamo a ottenere decisione comune.

Per favore, ricorda la prima tecnica, è molto comune e viene spesso utilizzato in compiti pratici: se dopo l'integrazione appare un logaritmo a destra, in molti casi (ma non sempre!) è consigliabile scrivere la costante anche sotto il logaritmo. Ed è SICURO da annotare se il risultato è solo logaritmi (come nell'esempio in esame).

Questo è, INVECE DI le voci sono solitamente scritte .

Perché è necessario? E per rendere più semplice esprimere “gioco”. Utilizzo della proprietà dei logaritmi . In questo caso:

Ora i logaritmi e i moduli possono essere rimossi:

La funzione è presentata esplicitamente. Questa è la soluzione generale.

Risposta: decisione comune: .

Le risposte a molte equazioni differenziali sono abbastanza facili da verificare. Nel nostro caso, questo viene fatto in modo abbastanza semplice, prendiamo la soluzione trovata e la differenziamo:

Quindi sostituiamo la derivata nell'equazione originale:

– si ottiene l’uguaglianza corretta, il che significa che la soluzione generale soddisfa l’equazione, che è ciò che occorre verificare.

Dando a una costante valori diversi, è possibile ottenere un numero infinito di soluzioni private equazione differenziale. È chiaro che una qualsiasi delle funzioni , , ecc. soddisfa l'equazione differenziale.

A volte viene chiamata la soluzione generale famiglia di funzioni. In questo esempio, la soluzione generale è una famiglia di funzioni lineari o, più precisamente, una famiglia di proporzionalità diretta.

Dopo una revisione approfondita del primo esempio, è opportuno rispondere ad alcune domande ingenue sulle equazioni differenziali:

1)In questo esempio, siamo riusciti a separare le variabili. È sempre possibile farlo? No, non sempre. E ancora più spesso le variabili non possono essere separate. Ad esempio, nel equazioni omogenee del primo ordine, è necessario prima sostituirlo. In altri tipi di equazioni, ad esempio in un'equazione lineare disomogenea del primo ordine, è necessario utilizzare varie tecniche e metodi per trovare una soluzione generale. Le equazioni a variabili separabili, che considereremo nella prima lezione, sono il tipo più semplice di equazioni differenziali.

2) È sempre possibile integrare un’equazione differenziale? No, non sempre. È molto facile trovare un’equazione “fantasiosa” che non può essere integrata; inoltre, ci sono integrali che non possono essere presi. Ma tali DE possono essere risolti approssimativamente utilizzando metodi speciali. D’Alembert e Cauchy garantiscono... ...ugh, lurkmore. Per leggere molto proprio adesso, avrei quasi aggiunto "dall'altro mondo".

3) In questo esempio, abbiamo ottenuto una soluzione sotto forma di integrale generale . È sempre possibile trovare una soluzione generale a partire da un integrale generale, cioè esprimere esplicitamente la “y”? No, non sempre. Per esempio: . Bene, come puoi esprimere "greco" qui?! In questi casi, la risposta dovrebbe essere scritta come integrale generale. Inoltre, a volte è possibile trovare una soluzione generale, ma è scritta in modo così complicato e goffo che è meglio lasciare la risposta sotto forma di integrale generale

4) ...forse per ora può bastare. Nel primo esempio che abbiamo incontrato un altro punto importante, ma per non ricoprire i “manichini” con una valanga di nuove informazioni, lo lascio alla prossima lezione.

Non avremo fretta. Un altro semplice telecomando e un'altra soluzione tipica:

Esempio 2

Trovare una soluzione particolare dell'equazione differenziale che soddisfi la condizione iniziale

Soluzione: in base alle condizioni, è necessario trovare soluzione privata DE che soddisfa una data condizione iniziale. Questa formulazione della domanda viene anche chiamata Problema di Cauchy.

Per prima cosa troviamo una soluzione generale. Non c'è alcuna variabile "x" nell'equazione, ma questo non dovrebbe creare confusione, l'importante è che abbia la derivata prima.

Riscriviamo la derivata nella forma richiesta:

Ovviamente le variabili possono essere separate, ragazzi a sinistra, ragazze a destra:

Integriamo l'equazione:

Si ottiene l'integrale generale. Qui ho disegnato una costante con un asterisco, fatto sta che molto presto si trasformerà in un'altra costante.

Proviamo ora a trasformare l'integrale generale in una soluzione generale (esprimere esplicitamente la “y”). Ricordiamo le belle vecchie cose della scuola: . In questo caso:

La costante nell'indicatore sembra in qualche modo poco kosher, quindi di solito viene riportata con i piedi per terra. Nel dettaglio, ecco come avviene. Usando la proprietà dei gradi, riscriviamo la funzione come segue:

Se è una costante, allora è anche una costante, ridesigniamola con la lettera :
– in questo caso rimuoviamo il modulo, dopodiché la costante “ce” può assumere sia valori positivi che negativi

Ricorda che "demolire" una costante lo è seconda tecnica, che viene spesso utilizzato quando si risolvono equazioni differenziali. Nella versione pulita puoi passare immediatamente da a, ma sii sempre pronto a spiegare questa transizione.

Quindi, la soluzione generale è: . Questa è una bella famiglia di funzioni esponenziali.

Nella fase finale, è necessario trovare una soluzione particolare che soddisfi la condizione iniziale data. Anche questo è semplice.

Qual è il compito? È necessario ritirare come il valore della costante in modo che la condizione sia soddisfatta.

Può essere formattato in diversi modi, ma questo sarà probabilmente il modo più chiaro. Nella soluzione generale, al posto della “X” sostituiamo uno zero, e al posto della “Y” sostituiamo un due:



Questo è,

Versione di design standard:

Ora sostituiamo il valore trovato della costante nella soluzione generale:
– questa è la soluzione particolare di cui abbiamo bisogno.

Risposta: soluzione privata:

Controlliamo. Il controllo di una soluzione privata prevede due fasi:

Per prima cosa è necessario verificare se la particolare soluzione trovata soddisfa davvero la condizione iniziale? Al posto della “X” sostituiamo uno zero e vediamo cosa succede:
- sì, in effetti, è stato ricevuto un due, il che significa che la condizione iniziale è soddisfatta.

La seconda fase è già familiare. Prendiamo la soluzione particolare risultante e troviamo la derivata:

Sostituiamo nell'equazione originale:

– si ottiene l’uguaglianza corretta.

Conclusione: la soluzione particolare è stata trovata correttamente.

Passiamo ad esempi più significativi.

Esempio 3

Risolvere l'equazione differenziale

Soluzione: Riscriviamo la derivata nella forma che ci serve:

Valutiamo se è possibile separare le variabili? Potere. Spostiamo il secondo termine a destra con cambio di segno:

E trasferiamo i moltiplicatori secondo la regola delle proporzioni:

Le variabili sono separate, integriamo entrambe le parti:

Devo avvisarti, il giorno del giudizio si avvicina. Se non hai studiato bene integrali indefiniti, hai risolto alcuni esempi, quindi non c'è nessun posto dove andare: ora dovrai padroneggiarli.

L'integrale del secondo membro è facile da trovare; trattiamo l'integrale della cotangente utilizzando la tecnica standard che abbiamo visto nella lezione Integrazione di funzioni trigonometriche l'anno scorso:

Di conseguenza, abbiamo ottenuto solo logaritmi e, secondo la mia prima raccomandazione tecnica, definiamo anche la costante come logaritmo.

Cerchiamo ora di semplificare l’integrale generale. Poiché disponiamo solo di logaritmi, è del tutto possibile (e necessario) eliminarli. Usando proprietà conosciute“Impacchettiamo” i logaritmi il più possibile. Lo scrivo dettagliatamente:

La confezione è finita per essere barbaramente sbrindellata:
, e subito ci presentiamo integrale generale A proposito, finché è possibile:

In genere non è necessario farlo, ma fa sempre bene accontentare il professore ;-)

In linea di principio, questo capolavoro può essere scritto come una risposta, ma qui è comunque opportuno elevare al quadrato entrambe le parti e ridisegnare la costante:

Risposta: integrale generale:

! Nota: L'integrale generale può spesso essere scritto in più di un modo. Pertanto, se il tuo risultato non coincide con la risposta precedentemente nota, ciò non significa che hai risolto l'equazione in modo errato.

È possibile esprimere “gioco”? Potere. Esprimiamo la soluzione generale:

Naturalmente il risultato ottenuto è adatto per una risposta, ma si noti che l'integrale generale appare più compatto e la soluzione è più breve.

Terzo consiglio tecnico:se per ottenere una soluzione generale è necessario eseguire un numero significativo di azioni, nella maggior parte dei casi è meglio astenersi da queste azioni e lasciare la risposta sotto forma di integrale generale. Lo stesso vale per le azioni “cattive”, quando occorre esprimere la funzione inversa, elevare a potenza, estrarre la radice, ecc. Il fatto è che la soluzione generale sembrerà pretenziosa e ingombrante, con grandi radici, segni e altri rifiuti matematici.

Come controllare? Il controllo può essere effettuato in due modi. Metodo uno: prendi la soluzione generale , troviamo la derivata e sostituiscili nell'equazione originale. Prova tu stesso!

Il secondo modo è differenziare l'integrale generale. È abbastanza semplice, l'importante è riuscire a trovarlo derivata di una funzione specificata implicitamente:

dividi ogni termine per:

e su:

L'equazione differenziale originale è stata ottenuta esattamente, il che significa che l'integrale generale è stato trovato correttamente.

Esempio 4

Trovare una soluzione particolare dell'equazione differenziale che soddisfi la condizione iniziale. Eseguire il controllo.

Questo è un esempio che puoi risolvere da solo.

Permettetemi di ricordarvi che l'algoritmo si compone di due fasi:
1) trovare una soluzione generale;
2) trovare la soluzione particolare richiesta.

Anche il controllo viene effettuato in due passaggi (vedi esempio nell'Esempio n. 2), è necessario:
1) assicurarsi che la particolare soluzione trovata soddisfi la condizione iniziale;
2) verificare che una particolare soluzione soddisfi generalmente l'equazione differenziale.

Soluzione completa e risposta alla fine della lezione.

Esempio 5

Trovare una soluzione particolare dell'equazione differenziale , soddisfacendo la condizione iniziale. Eseguire il controllo.

Soluzione: Per prima cosa troviamo una soluzione generale: questa equazione contiene già i differenziali già pronti e, quindi, la soluzione è semplificata. Separiamo le variabili:

Integriamo l'equazione:

L'integrale a sinistra è tabulare, si prende l'integrale a destra Metodo per sussumere una funzione sotto il segno differenziale:

L'integrale generale è stato ottenuto; è possibile esprimere con successo la soluzione generale? Potere. Appendiamo i logaritmi su entrambi i lati. Poiché sono positivi, i segni del modulo non sono necessari:

(Spero che tutti comprendano la trasformazione, queste cose dovrebbero già essere conosciute)

Quindi la soluzione generale è:

Troviamo una soluzione particolare corrispondente alla condizione iniziale data.
Nella soluzione generale, invece di “X” sostituiamo zero, e invece di “Y” sostituiamo il logaritmo di due:

Design più familiare:

Sostituiamo il valore trovato della costante nella soluzione generale.

Risposta: soluzione privata:

Verifica: innanzitutto controlliamo se la condizione iniziale è soddisfatta:
- va tutto bene.

Ora controlliamo se la soluzione particolare trovata soddisfa del tutto l’equazione differenziale. Trovare la derivata:

Consideriamo l'equazione originale: – è presentato in differenziale. Esistono due modi per verificare. È possibile esprimere il differenziale dalla derivata trovata:

Sostituiamo la soluzione particolare trovata e il differenziale risultante nell'equazione originale :

Usiamo l'identità logaritmica di base:

Si ottiene l'uguaglianza corretta, il che significa che la soluzione particolare è stata trovata correttamente.

Il secondo metodo di controllo è speculare e più familiare: dall'equazione Esprimiamo la derivata, per fare questo dividiamo tutti i pezzi per:

E nel DE trasformato sostituiamo la soluzione parziale ottenuta e il derivato trovato. Come risultato delle semplificazioni, si dovrebbe ottenere anche l'uguaglianza corretta.

Esempio 6

Trova l'integrale generale dell'equazione, presenta la risposta nel modulo.

Questo è un esempio che puoi risolvere da solo, completa la soluzione e rispondi alla fine della lezione.

Quali difficoltà si nascondono quando si risolvono equazioni differenziali con variabili separabili?

1) Non è sempre ovvio (soprattutto per una “teiera”) che le variabili possano essere separate. Consideriamo un esempio condizionale: . Qui devi togliere i fattori tra parentesi: e separare le radici: . È chiaro cosa fare dopo.

2) Difficoltà con l'integrazione stessa. Gli integrali spesso non sono i più semplici e se ci sono difetti nella capacità di trovarli integrale indefinito, allora sarà difficile con molti diffusori. Inoltre, la logica "poiché l'equazione differenziale è semplice, almeno lasciamo che gli integrali siano più complicati" è popolare tra i compilatori di raccolte e manuali di formazione.

3) Trasformazioni con una costante. Come tutti hanno notato, la costante nelle equazioni differenziali può essere gestita abbastanza liberamente e alcune trasformazioni non sono sempre chiare a un principiante. Consideriamo un altro esempio condizionale: . Si consiglia di moltiplicare tutti i termini per 2: . La costante risultante è anche una sorta di costante, che può essere denotata da: . Sì, e poiché abbiamo solo logarim, è consigliabile riscrivere la costante sotto forma di un'altra costante: .

Il problema è che spesso non si preoccupano degli indici e usano la stessa lettera. Di conseguenza, il verbale della decisione assume la seguente forma:

Che diamine?! Ci sono errori proprio lì! A rigor di termini, sì. Tuttavia, da un punto di vista sostanziale, non ci sono errori, perché trasformando una variabile costante si ottiene una variabile costante equivalente.

Oppure un altro esempio: supponiamo che nel corso della risoluzione dell'equazione si ottenga un integrale generale. Questa risposta sembra brutta, quindi è consigliabile cambiare il segno di ogni termine: . Formalmente qui c'è un altro errore: dovrebbe essere scritto a destra. Ma informalmente resta inteso che “meno ce” è pur sempre una costante, che assume anche lo stesso insieme di valori, e quindi non ha senso mettere “meno”.

Cercherò di evitare un approccio imprudente e di assegnare comunque indici diversi alle costanti durante la conversione. Che è quello che ti consiglio di fare.

Esempio 7

Risolvere l'equazione differenziale. Eseguire il controllo.

Soluzione: Questa equazione consente la separazione delle variabili. Separiamo le variabili:

Integriamo:

Non è necessario definire qui la costante come logaritmo, poiché non ne verrà fuori nulla di utile.

Risposta: integrale generale:

E, naturalmente, non è necessario esprimere qui esplicitamente la "y", perché si rivelerà spazzatura (ricorda il terzo suggerimento tecnico).

Visita medica: Differenziare la risposta (funzione implicita):

Eliminiamo le frazioni moltiplicando entrambi i termini per:

È stata ottenuta l'equazione differenziale originale, il che significa che l'integrale generale è stato trovato correttamente.

Esempio 8

Trova una soluzione particolare del DE.
,