Historia e origjinës së teorisë së grafikut. Historia e shfaqjes dhe zhvillimit të teorisë së grafikut. Teoria e grafikut dhe problemet më të rëndësishme moderne të aplikuara

GRAFIKE

Shumë probleme vijnë në shqyrtimin e një grupi objektesh, vetitë thelbësore të të cilave përshkruhen nga lidhjet midis tyre. Për shembull, duke parë një hartë rrugore, dikush mund të interesohet vetëm nëse ka një lidhje midis vendbanimeve të caktuara, duke injoruar konfigurimin dhe cilësinë e rrugëve, distancat dhe detajet e tjera. Gjatë studimit të qarqeve elektrike mund të dalin në pah natyra e lidhjeve të komponentëve të ndryshëm të tij - rezistencave, kondensatorëve, burimeve etj.. Molekulat organike formojnë struktura, vetitë karakteristike të të cilave janë lidhjet ndërmjet atomeve. Me interes mund të jenë lidhjet dhe marrëdhëniet e ndryshme midis njerëzve, ngjarjeve, gjendjeve dhe, në përgjithësi, midis çdo objekti.

Në raste të tilla, është e përshtatshme të përshkruhen objektet në shqyrtim si pika, dhe lidhjet midis tyre si linja të konfigurimit arbitrar. Një imazh i tillë i formalizuar quhet grafik (nga greqishtja grajw - shkruaj).

Oriz. 4.1 .

Puna e parë mbi grafikët u botua nga njëzetvjeçari Leonhard Euler në 1736, ndërsa ai punonte në Akademinë Ruse të Shkencave. Ai përmbante një zgjidhje për problemin e urave Königsberg (Fig. 4.1a): a është e mundur të bëni një shëtitje në atë mënyrë që, duke lënë çdo vend në qytet, të mund të ktheheni në të duke ecur saktësisht një herë mbi secilën urë ? Është e qartë se sipas kushteve të problemit, nuk ka rëndësi se si kalon shtegu nëpër pjesë të tokës a, b, c, d, në të cilën ndodhet qyteti i Koenigsberg (tani Kaliningrad), kështu që ato mund të jenë të përfaqësuar si kulme. Dhe meqenëse lidhjet midis këtyre pjesëve kryhen vetëm përmes shtatë urave, secila prej tyre përfaqësohet nga një skaj që lidh kulmet përkatëse. Si rezultat, marrim grafikun e treguar në Fig. 4.1b. Euler i dha një përgjigje negative pyetjes së parashtruar. Për më tepër, ai vërtetoi se një rrugë e tillë ekziston vetëm për një grafik të tillë që çdo kulm i tij të lidhet me një numër çift skajesh.

Teoria e grafikut mori shtysën e saj të radhës pothuajse 100 vjet më vonë me zhvillimin e kërkimit në rrjetet elektrike, kristalografinë, kiminë organike dhe shkenca të tjera. Së bashku me enigmat e shumta dhe lojërat me grafik, u morën parasysh probleme të rëndësishme praktike, shumë prej të cilave kërkonin teknika të sofistikuara matematikore. Tashmë në mesin e shekullit të kaluar, Kirchhoff përdori grafikë për të analizuar qarqet elektrike dhe Cayley eksploroi një klasë të rëndësishme grafikësh për identifikimin dhe renditjen e izomerëve të hidrokarbureve të ngopura. Megjithatë, teoria e grafikëve si disiplinë matematikore u formua vetëm në mesin e viteve tridhjetë të shekullit të kaluar falë punës së shumë studiuesve, merita më e madhe ndër të cilët i përket D. Koenig. Kontribut të rëndësishëm në teorinë e grafikut dhanë shkencëtarët sovjetikë L. S. Pontryagin, A. A. Zykov, V. G. Vising dhe të tjerë.

Pa e vënë re, ne ndeshim grafikë gjatë gjithë kohës. Për shembull, një grafik është një diagram i linjave të metrosë. Pikat në të përfaqësojnë stacione, dhe linjat përfaqësojnë rrugët e trenit. Duke hulumtuar prejardhjen tonë dhe duke e gjurmuar atë tek paraardhësit tanë, ne ndërtojmë një pemë familjare. Dhe kjo pemë është një grafik.

Grafikët shërbejnë si një mjet i përshtatshëm për të përshkruar marrëdhëniet midis objekteve. Për shembull, duke marrë në konsideratë një grafik që përshkruan një rrjet rrugësh midis zonave të populluara, mund të përcaktoni itinerarin nga pika A në pikën B. Nëse ka disa rrugë të tilla, ju dëshironi të zgjidhni atë optimale në një kuptim të caktuar, për shembull më e shkurtra apo më e sigurta. Për të zgjidhur problemin e përzgjedhjes, është e nevojshme të kryhen llogaritje të caktuara në grafikë. Kur zgjidhni probleme të tilla, është e përshtatshme të përdorni teknika algjebrike dhe vetë koncepti i një grafiku duhet të zyrtarizohet.

Teoria e grafikut ka një mjet të fuqishëm për zgjidhjen e problemeve të aplikuara nga një shumëllojshmëri e gjerë fushash të shkencës dhe teknologjisë. Kjo përfshin, për shembull, analizën dhe sintezën e qarqeve dhe sistemeve, projektimin e kanaleve të komunikimit dhe studimin e proceseve të transferimit të informacionit, ndërtimin e qarqeve të kontaktit dhe studimin e makinave në gjendje të fundme, planifikimin dhe kontrollin e rrjetit, kërkimin e operacioneve, përzgjedhja e rrugëve dhe flukseve optimale në rrjete, studimi i proceseve të rastësishme dhe shumë detyra të tjera. Teoria e grafikut është e lidhur ngushtë me degë të tilla të matematikës diskrete si teoria e grupeve, teoria e matricës, logjika matematikore dhe teoria e probabilitetit.

Aktualisht, teoria e grafikëve mbulon shumë materiale, por kur e paraqesim atë, ne do të kufizohemi vetëm në një pjesë të tij dhe, duke lënë jashtë teoremave të shumta, do të shqyrtojmë vetëm disa konceptet bazë.

Leonard Euler konsiderohet themeluesi i teorisë së grafeve. Në 1736, në një nga letrat e tij, ai formuloi dhe propozoi një zgjidhje për problemin e shtatë urave të Königsberg, e cila më vonë u bë një nga problemet klasike të teorisë së grafikëve.

Problemet e para në teorinë e grafikëve lidheshin me zgjidhjen e problemeve matematikore rekreative dhe enigmave. Këtu është një ritregim i një fragmenti nga letra e Euler-it të datës 13 mars 1736: “Më dhanë një problem për një ishull që ndodhet në qytetin e Königsberg dhe i rrethuar nga një lumë me 7 ura përtej tij. Pyetja është nëse dikush mund t'i rrotullojë vazhdimisht, duke kaluar vetëm një herë mbi secilën urë. Dhe pastaj u informova se askush nuk kishte mundur ta bënte këtë ende, por askush nuk e kishte vërtetuar se ishte e pamundur. Kjo pyetje, edhe pse e parëndësishme, më dukej, megjithatë, e denjë për vëmendje, sepse as gjeometria, as algjebra, as arti kombinues nuk mjaftojnë për ta zgjidhur atë. Pas shumë mendimeve, gjeta një rregull të lehtë, të bazuar në një provë plotësisht bindëse, me ndihmën e së cilës është e mundur, në të gjitha problemet e këtij lloji, të përcaktohet menjëherë nëse një shmangie e tillë mund të bëhet përmes ndonjë numri dhe çdo numri ura të vendosura në çfarëdo mënyre ose jo.” Urat e Königsberg mund të përshkruhen skematikisht si më poshtë:

Rregulli i Euler:

1. Në një grafik që nuk ka kulme me shkallë tek, ka një kalim të të gjitha skajeve (dhe çdo skaj përshkohet saktësisht një herë) duke filluar nga çdo kulm i grafikut.

2. Në një graf që ka dy dhe vetëm dy kulme me shkallë tek, ka një përshkim që fillon në një kulm me shkallë tek dhe përfundon në tjetrin.

3. Në një grafik që ka më shumë se dy kulme me shkallë tek, një përshkim i tillë nuk ekziston.

Ekziston një lloj tjetër problemi që lidhet me udhëtimin përgjatë grafikëve. Ne po flasim për probleme në të cilat është e nevojshme të gjesh një shteg që kalon nëpër të gjitha kulmet, dhe jo më shumë se një herë nëpër secilën. Një cikël që kalon nëpër çdo kulm një herë dhe vetëm një herë quhet një vijë Hamiltoniane (pas William Rowan Hamilton, matematikani i famshëm irlandez i shekullit të kaluar i cili ishte i pari që studioi linja të tilla). Fatkeqësisht, ende nuk është gjetur një kriter i përgjithshëm me ndihmën e të cilit mund të vendoset nëse një grafik i caktuar është Hamiltonian, dhe nëse po, atëherë gjeni të gjitha linjat Hamiltoniane në të.

Formuluar në mesin e shekullit të 19-të. Problemi me katër ngjyra duket gjithashtu si një problem zbavitës, por përpjekjet për ta zgjidhur atë kanë çuar në disa studime grafike që kanë rëndësi teorike dhe aplikative. Problemi me katër ngjyra është formuluar si më poshtë: "A mund të ngjyroset një zonë e çdo harte të sheshtë me katër ngjyra në mënyrë që çdo dy zona ngjitur të ngjyrosen me ngjyra të ndryshme?" Hipoteza se përgjigja është pohuese u formulua në mesin e shekullit të 19-të. Në vitin 1890, u vërtetua një deklaratë më e dobët, domethënë se çdo hartë e sheshtë mund të ngjyroset në pesë ngjyra. Duke lidhur çdo hartë planare me grafikun e saj të dyfishtë planar, marrim një formulim ekuivalent të problemit për sa i përket grafikëve: A është e vërtetë që numri kromatik i çdo grafi planar është më i vogël ose i barabartë me katër? Përpjekje të shumta për të zgjidhur problemin ndikuan në zhvillimin e një sërë fushash të teorisë së grafikëve. Në vitin 1976, u njoftua një zgjidhje pozitive për problemin duke përdorur një kompjuter.

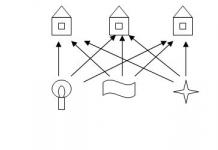
Një tjetër problem i vjetër topologjik që ka qenë veçanërisht rezistent ndaj zgjidhjes për një kohë të gjatë dhe që ka përhumbur mendjet e adhuruesve të enigmës njihet si "problemi i furnizimit me energji elektrike, gaz dhe ujë". Në vitin 1917, Henry E. Dudeney i dha këtë formulim. Gazi, energjia elektrike dhe uji duhet të instalohen në secilën nga tre shtëpitë e paraqitura në figurë.

Teoria e grafikut. 1

Historia e shfaqjes së teorisë së grafikut. 1

Rregulli i Euler-it. 1

Letërsia

1. Teoria e grafikut Belov, Moska, "Shkenca", 1968.

2. Teknologjitë e reja pedagogjike dhe informative E.S. Polat , Moskë, "Akademia" 1999

3. Kuznetsov O.P., Adelson-Velsky G.M. Matematikë diskrete për inxhinierin. - M.: Energoatomizdat, 1988.

4. Cook D., Baze G. Matematikë kompjuterike. - M.: Shkencë, 1990.

5. Nefedov V.N., Osipova V.A. Kurs diskrete i matematikës. - M.: Shtëpia Botuese MAI, 1992.

6. Ore O. Teoria e grafikut. - M.: Shkencë, 1980.

7. Ismagilov R.S., Kalinkin A.V. Materiale për mësimet praktike në lëndën: Matematikë diskrete

Teoria e grafikut- kapitulli matematikë diskrete, duke studiuar pronat grafikët . Në një kuptim të përgjithshëm, një grafik përfaqësohet si një grup kulmesh (nyjesh) të lidhura me skaje. Në një përkufizim të rreptë, një çift i tillë grupesh quhet graf. G=(V,E), ku V është një nëngrup i çdo grupi të numërueshëm dhe E është një nëngrup i V×V.

Historia e teorisë së grafikëve
Leonard Euler konsiderohet themeluesi i teorisë së grafeve. Në 1736, në një nga letrat e tij, ai formuloi dhe propozoi një zgjidhje për problemin e shtatë urave të Königsberg, e cila më vonë u bë një nga problemet klasike të teorisë së grafikëve.
Problemet e para në teorinë e grafikëve lidheshin me zgjidhjen e problemeve matematikore rekreative dhe enigmave. Këtu është një ritregim i një fragmenti nga letra e Euler-it të datës 13 mars 1736: “Më dhanë një problem për një ishull që ndodhet në qytetin e Königsberg dhe i rrethuar nga një lumë me 7 ura përtej tij. Pyetja është nëse dikush mund t'i rrotullojë vazhdimisht, duke kaluar vetëm një herë mbi secilën urë. Dhe pastaj u informova se askush nuk kishte mundur ta bënte këtë ende, por askush nuk e kishte vërtetuar se ishte e pamundur. Kjo pyetje, edhe pse e parëndësishme, më dukej, megjithatë, e denjë për vëmendje, sepse as gjeometria, as algjebra, as arti kombinues nuk mjaftojnë për ta zgjidhur atë. Pas shumë mendimeve, gjeta një rregull të lehtë, të bazuar në një provë plotësisht bindëse, me ndihmën e së cilës është e mundur, në të gjitha problemet e këtij lloji, të përcaktohet menjëherë nëse një shmangie e tillë mund të bëhet përmes ndonjë numri dhe çdo numri ura të vendosura në çfarëdo mënyre ose jo.” Urat e Königsberg mund të përshkruhen skematikisht si më poshtë:
Rregulli i Euler:

1. Në një grafik që nuk ka kulme të shkallëve tek, ka një kalim të të gjitha skajeve (dhe çdo skaj përshkohet saktësisht një herë) duke filluar nga çdo kulm i grafikut.
2. Në një graf që ka dy dhe vetëm dy kulme me shkallë tek, ka një përshkim që fillon në një kulm me shkallë tek dhe përfundon në tjetrin.
3. Në një grafik që ka më shumë se dy kulme me shkallë tek, një përshkim i tillë nuk ekziston.

viti shkollor 2016 viti

1. Hyrje

2. Historia e shfaqjes së teorisë së grafikut

3. Konceptet bazë të teorisë së grafeve

4. Teoremat bazë të teorisë së grafeve

5. Metodat e paraqitjes së grafikëve në kompjuter

6. Rishikimi i problemeve të teorisë së grafikëve

7. Përfundim

8. Referencat

Prezantimi

Kohët e fundit, kërkimet në fushat tradicionalisht të lidhura me matematikën diskrete janë bërë gjithnjë e më të spikatura. Së bashku me seksione të tilla klasike të matematikës si analiza matematikore dhe ekuacionet diferenciale, në kurrikulat e specialitetit "Matematikë e Aplikuar" dhe shumë specialitete të tjera janë shfaqur seksione për logjikën matematikore, algjebër, kombinatorikën dhe teorinë e grafikëve. Arsyet për këtë nuk janë të vështira për t'u kuptuar thjesht duke identifikuar gamën e problemeve të zgjidhura në bazë të këtij aparati matematikor.

Historia e shfaqjes së teorisë së grafikut.

1. Problem në lidhje me urat Königsberg. Në Fig. 1 tregon një plan skematik të pjesës qendrore të qytetit të Koenigsberg (tani Kaliningrad), duke përfshirë dy brigje të lumit Pergola, dy ishuj në të dhe shtatë ura lidhëse. Detyra është që të rrotullohen të katër pjesët e tokës, duke kaluar çdo urë një herë dhe të ktheheni në pikën e fillimit. Ky problem u zgjidh (u tregua se nuk kishte zgjidhje) nga Euler në 1736.

oriz. 1

2. Problemi i tre shtëpive dhe tre puseve. Ka tre shtëpi dhe tre puse, të vendosura disi në një avion. Vizatoni një shteg nga çdo shtëpi në çdo pus në mënyrë që shtigjet të mos kryqëzohen (Fig. 2). Ky problem u zgjidh (u tregua se nuk ka zgjidhje) nga Kuratovsky në 1930.

oriz. 2

3. Problemi me katër ngjyra. Ndarja e një aeroplani në zona që nuk mbivendosen quhet hartë. Zonat në një hartë quhen ngjitur nëse kanë një kufi të përbashkët. Detyra është të ngjyrosni hartën në mënyrë të tillë që të mos pikturohen dy zona ngjitur me të njëjtën ngjyrë (Fig. 3). Që nga fundi i shekullit të kaluar, hipoteza është e njohur se katër ngjyra janë të mjaftueshme për këtë. Në vitin 1976, Appel dhe Heiken publikuan një zgjidhje për problemin me katër ngjyra, e cila bazohej në një kërkim kompjuterik. Zgjidhja e këtij problemi “në mënyrë programore” ishte një precedent që shkaktoi një diskutim të nxehtë, i cili nuk ka mbaruar aspak. Thelbi i zgjidhjes së publikuar është të provoni një numër të madh, por të kufizuar (rreth 2000) lloje kundërshembujsh të mundshëm ndaj teoremës me katër ngjyra dhe të tregoni se asnjë rast i vetëm nuk është kundërshembull. Ky kërkim u përfundua nga programi në rreth një mijë orë funksionim të superkompjuterit. Është e pamundur të kontrollohet zgjidhja që rezulton "me dorë" - fushëveprimi i numërimit shkon shumë përtej aftësive njerëzore. Shumë matematikanë ngrenë pyetjen: a mund të konsiderohet një "provë programi" e tillë një provë e vlefshme? Në fund të fundit, mund të ketë gabime në program... Metodat për të vërtetuar zyrtarisht korrektësinë e programeve nuk janë të zbatueshme për programet e një kompleksiteti të tillë si ai që diskutohet. Testimi nuk mund të garantojë mungesën e gabimeve dhe në këtë rast është përgjithësisht i pamundur. Kështu, ne mund të mbështetemi vetëm në aftësitë programuese të autorëve dhe të besojmë se ata bënë gjithçka siç duhet.

Oriz. 3

Konceptet bazë të teorisë së grafikëve

1) Grafiku G(V,E)është një koleksion i dy grupeve - një grup jo bosh V (bashkësi kulmesh) dhe një grup E i nëngrupeve me dy elemente të grupit V (E - grup i skajeve).

2) I orientuarështë një grafik në të cilin është një grup çiftesh të renditura kulmesh të formës (x,y), ku x quhet fillimi dhe y është fundi i harkut. Harku (x, y) shpesh shkruhet si . Ata gjithashtu thonë se harku çon nga kulmi x në kulmin y, dhe kulmin y ngjitur me kulmin x.

3) Nëse një element i bashkësisë E mund të jetë një çift identike elemente (jo të dallueshme) të V-së, atëherë quhet një element i tillë i bashkësisë E lak, dhe thirret grafiku grafiku me sythe(ose pseudograf).

4) Nëse E nuk është një grup, por vendosur që përmban disa elemente identike, atëherë këto elemente quhen skajet e shumta, dhe thirret grafiku multigraf.

5) Nëse elementet e bashkësisë E nuk janë domosdoshmërisht dy elementësh, por çdo nënbashkësi e bashkësisë V, atëherë elementët e tillë të grupit E quhen hiperarket, dhe thirret grafiku hipergrafi.

6) Nëse funksioni është i specifikuar F: V → M dhe/ose F: E → M, pastaj grupi M quhet një grup shënime, dhe thirret grafiku e shënuar(ose i ngarkuar). Grupi i shenjave është zakonisht shkronja ose numra të plotë. Nëse funksioni Fështë injektiv, pra kulme (skajet) të ndryshme kanë etiketa të ndryshme, atëherë grafiku quhet të numëruara.

7) Nëngrafi quhet grafiku G′(V′,E′), ku dhe/ose .

a) Nëse V′ = V, atëherë thirret G′ bërthamë nëngrafi G.

b) Nëse , atëherë thirret grafi G′ vet nëngrafi i grafikut G.

c) Një nëngraf G′(V′,E′) quhet nëngraf i rregullt i grafikut G(V,E) nëse G′ përmban të gjitha skajet e mundshme të G.

8) Shkalla (valencë) kulmet është numri i skajeve që bien në këtë kulm (numri i kulmeve ngjitur me të).

9) Itinerari në një grafik është një sekuencë e alternuar e kulmeve dhe e skajeve në të cilën çdo dy elemente ngjitur janë incidente.

a) Nëse , atëherë rruga mbyllur, ndryshe hapur.

b) Nëse të gjitha skajet janë të ndryshme, atëherë thirret rruga zinxhir.

c) Nëse të gjitha kulmet (dhe rrjedhimisht skajet) janë të ndryshme, atëherë thirret rruga zinxhir i thjeshtë.

d) Quhet qark i mbyllur ciklit.

e) Quhet qark i thjeshtë i mbyllur lak i thjeshtë.

f) Quhet një graf pa cikle aciklike.

g) Për digrafët, zinxhiri quhet nga, dhe cikli është përvijojnë.

oriz. 4. Rrugët, zinxhirët, ciklet

Shembull

Në grafikun, diagrami i të cilit është paraqitur në Fig. 4:

1. v 1, v 3, v 1, v 4 - një rrugë, por jo një qark;

2. v 1, v 3, v 5, v 2, v 3, v 4 – një zinxhir, por jo një zinxhir i thjeshtë;

3. v 1, v 4, v 3, v 2, v 5 – zinxhir i thjeshtë;

4. v 1, v 3, v 5, v 2, v 3, v 4, v 1 – një cikël, por jo një cikël i thjeshtë;

5. v 1 , v 3 , v 4 , v 1 - një cikël i thjeshtë.

10) Nëse një grafik ka një cikël (jo domosdoshmërisht të thjeshtë) që përmban të gjitha skajet e grafikut një herë, atëherë një cikël i tillë quhet Eulerian ciklit.

11) Nëse një grafik ka një cikël të thjeshtë që përmban të gjitha kulmet e grafikut (një nga një), atëherë një cikël i tillë quhet Hamiltonian ciklit.

12) pemë quhet graf i lidhur pa cikle.

13) skelet Një pemë që përmban të gjitha kulmet e një grafi quhet.

14) Përputhjaështë një grup skajesh në të cilat nuk ka dy ngjitur.

15) Përputhja quhet maksimale, nëse asnjë superbashkësi e tij nuk është e pavarur.

16) Dy kulme në një grafik lidhur, nëse ka një zinxhir të thjeshtë që i lidh ato.

17) Një graf në të cilin të gjitha kulmet janë të lidhura quhet koherente.

18) Një graf që përbëhet vetëm nga kulme të izoluara quhet mjaft jokoherente.

19) Gjatësia e rrugës numri i skajeve në të quhet (me përsëritje).

20) Largësia ndërmjet kulmeve u dhe v quhet gjatësia e vargut më të shkurtër dhe vetë zinxhiri më i shkurtër gjeodezike.

21) Diametri e një grafi G quhet gjatësia e gjeodezit më të gjatë.

22) Ekscentricitet kulmi v në një graf të lidhur G(V,E) është distanca maksimale nga kulmi v në kulmet e tjera të grafikut G.

23) Rrezja i një grafi G quhet më i vogli i ekscentriciteteve të kulmeve.

24) Kulmi v quhet qendrore, nëse ekscentriciteti i tij përkon me rrezen e grafikut.

25) Bashkësia e kulmeve qendrore quhet qendër grafiku.

oriz. 5 Ekscentricitetet e kulmeve dhe qendrave të grafikëve (të theksuara).

Informacione të lidhura.

Teoria e grafikut gjen zbatim, për shembull, në sistemet e informacionit gjeografik (GIS). Shtëpitë, strukturat, blloqet, etj. ekzistuese ose të reja të projektuara konsiderohen si kulme dhe rrugët, rrjetet komunale, linjat e energjisë elektrike etj. që i lidhin konsiderohen si skaje. Përdorimi i llogaritjeve të ndryshme të kryera në një grafik të tillë lejon, për shembull, të gjeni rrugën më të shkurtër të devijimit ose dyqanin ushqimor më të afërt, ose të planifikoni rrugën optimale.

Teoria e grafikut përmban një numër të madh problemesh të pazgjidhura dhe hipoteza ende të paprovuara.

Historia e teorisë së grafikëve

Leonard Euler konsiderohet themeluesi i teorisë së grafeve. Në 1736, në një nga letrat e tij, ai formuloi dhe propozoi një zgjidhje për problemin e shtatë urave të Königsberg, e cila më vonë u bë një nga problemet klasike të teorisë së grafikëve. Termi "graf" u krijua për herë të parë nga Sylvester, James Joseph në 1878 në artikullin e tij në Nature [ ] .

Terminologjia e teorisë së grafikut

Zbatimi i teorisë së grafikut

Shiko gjithashtu

Shënime

Letërsia

• Distel R. Teoria e grafikut Trans. nga anglishtja - Novosibirsk: Shtëpia Botuese e Institutit të Matematikës, 2002. - 336 f. ISBN 5-86134-101-X.
• Diestel R. Teoria e Grafikut, Botim Elektronik. - NY: Springer-Verlag, 2005. - F. 422.
• Basaker R., Saati T. Grafikët dhe rrjetet e fundme. M.: Nauka, 1974. 368c.
• Belov V.V., Vorobiev E.M., Shatalov V.E. Teoria e grafikut. - M.: Më e lartë. shkolla, 1976. - F. 392.
• Berge K. Teoria e grafikut dhe aplikimet e saj. M.: IL, 1962. 320c.
• Emelichev V. A., Melnikov O. I., Sarvanov V. I., Tyshkevich R. I. Leksione mbi teorinë e grafikëve. M.: Nauka, 1990. 384 f. (Ed. 2, rishikuar M.: URSS, 2009. 392 f.)