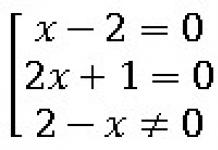Educational project "equations in OGE assignments." Solving quadratic equations I will solve oge quadratic equations

Quadratic equations are studied in 8th grade, so there is nothing complicated here. The ability to solve them is absolutely necessary.

A quadratic equation is an equation of the form ax 2 + bx + c = 0, where the coefficients a, b and c are arbitrary numbers, and a ≠ 0.

Before studying specific solution methods, note that all quadratic equations can be divided into three classes:

Have no roots;
Have exactly one root;
They have two different roots.

This is an important difference between quadratic equations and linear ones, where the root always exists and is unique. How to determine how many roots an equation has? There is a wonderful thing for this - discriminant.

Discriminant

Let the quadratic equation ax 2 + bx + c = 0 be given. Then the discriminant is simply the number D = b 2 − 4ac.

You need to know this formula by heart. Where it comes from is not important now. Another thing is important: by the sign of the discriminant you can determine how many roots a quadratic equation has. Namely:

If D< 0, корней нет;
If D = 0, there is exactly one root;
If D > 0, there will be two roots.

Please note: the discriminant indicates the number of roots, and not at all their signs, as for some reason many people believe. Take a look at the examples and you will understand everything yourself:

Task. How many roots do quadratic equations have:

x 2 − 8x + 12 = 0;

5x 2 + 3x + 7 = 0;

x 2 − 6x + 9 = 0.

Let's write out the coefficients for the first equation and find the discriminant:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 1 12 = 64 − 48 = 16

So the discriminant is positive, so the equation has two different roots. We analyze the second equation in a similar way:
a = 5; b = 3; c = 7;
D = 3 2 − 4 5 7 = 9 − 140 = −131.

The discriminant is negative, there are no roots. The last equation left is:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 1 9 = 36 − 36 = 0.

The discriminant is zero - the root will be one.

Please note that coefficients have been written down for each equation. Yes, it’s long, yes, it’s tedious, but you won’t mix up the odds and make stupid mistakes. Choose for yourself: speed or quality.

By the way, if you get the hang of it, after a while you won’t need to write down all the coefficients. You will perform such operations in your head. Most people start doing this somewhere after 50-70 solved equations - in general, not that much.

Roots of a quadratic equation

Now let's move on to the solution itself. If the discriminant D > 0, the roots can be found using the formulas:

Basic formula for the roots of a quadratic equation

When D = 0, you can use any of these formulas - you will get the same number, which will be the answer. Finally, if D< 0, корней нет — ничего считать не надо.

x 2 − 2x − 3 = 0;

15 − 2x − x 2 = 0;

x 2 + 12x + 36 = 0.

First equation:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 1 (−3) = 16.

D > 0 ⇒ the equation has two roots. Let's find them:

Second equation:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ the equation again has two roots. Let's find them

\[\begin(align) & ((x)_(1))=\frac(2+\sqrt(64))(2\cdot \left(-1 \right))=-5; \\ & ((x)_(2))=\frac(2-\sqrt(64))(2\cdot \left(-1 \right))=3. \\ \end(align)\]

Finally, the third equation:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 1 36 = 0.

D = 0 ⇒ the equation has one root. Any formula can be used. For example, the first one:

As you can see from the examples, everything is very simple. If you know the formulas and can count, there will be no problems. Most often, errors occur when substituting negative coefficients into the formula. Here again, the technique described above will help: look at the formula literally, write down each step - and very soon you will get rid of errors.

Incomplete quadratic equations

It happens that a quadratic equation is slightly different from what is given in the definition. For example:

x 2 + 9x = 0;
x 2 − 16 = 0.

It is easy to notice that these equations are missing one of the terms. Such quadratic equations are even easier to solve than standard ones: they don’t even require calculating the discriminant. So, let's introduce a new concept:

The equation ax 2 + bx + c = 0 is called an incomplete quadratic equation if b = 0 or c = 0, i.e. the coefficient of the variable x or the free element is equal to zero.

Of course, a very difficult case is possible when both of these coefficients are equal to zero: b = c = 0. In this case, the equation takes the form ax 2 = 0. Obviously, such an equation has a single root: x = 0.

Let's consider the remaining cases. Let b = 0, then we obtain an incomplete quadratic equation of the form ax 2 + c = 0. Let us transform it a little:

Since the arithmetic square root exists only of a non-negative number, the last equality makes sense only for (−c /a) ≥ 0. Conclusion:

If in an incomplete quadratic equation of the form ax 2 + c = 0 the inequality (−c /a) ≥ 0 is satisfied, there will be two roots. The formula is given above;
If (−c /a)< 0, корней нет.

As you can see, a discriminant was not required—there are no complex calculations at all in incomplete quadratic equations. In fact, it is not even necessary to remember the inequality (−c /a) ≥ 0. It is enough to express the value x 2 and see what is on the other side of the equal sign. If there is a positive number, there will be two roots. If it is negative, there will be no roots at all.

Now let's look at equations of the form ax 2 + bx = 0, in which the free element is equal to zero. Everything is simple here: there will always be two roots. It is enough to factor the polynomial:

Taking the common factor out of brackets

The product is zero when at least one of the factors is zero. This is where the roots come from. In conclusion, let’s look at a few of these equations:

Task. Solve quadratic equations:

x 2 − 7x = 0;

5x 2 + 30 = 0;

4x 2 − 9 = 0.

x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.

5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. There are no roots, because a square cannot be equal to a negative number.

4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1.5; x 2 = −1.5.

Teacher : Yurgenson Veronica Alexandrovna

Class: 9

Item: Algebra

Lesson topic: Preparation lesson for the OGE in grade 9 “Quadratic equations.”

Stage of training on this topic : preparation for the OGE.

Lesson type: Lesson on generalization and systematization of knowledge

Target:

Activity: Formation of students' skills to implement regulatory methods of action.

Content: - practicing methods for solving quadratic equations;

Developing the ability to choose the most rational solution;

Developmental: to form key competencies of students: information (the ability to analyze information, compare, draw conclusions), problem-solving (the ability to pose problems and, using existing knowledge, find a way out of the situation); communicative (ability to work in groups, ability to listen and hear others, accept the opinions of others)

Tasks for the teacher:

To help update students’ knowledge about solving quadratic equations;

Organize educational activities to practice ways to solve quadratic equations;

Create conditions for the formation of skills to develop the ability to choose the most rational solution;

Create conditions for the formation of regulatory UUD: goal setting, self-esteem and self-control, planning.

Technology: Multi-level training

Teaching methods: Visual, verbal, method of mutual verification, method of jointly finding an optimal solution, temporary work in groups, creating a problem situation, reproductive (instruction, illustration, explanation, practical training). Methods of self-control.

Used forms of organizing students' cognitive activity:

Collective form of work (frontal questioning, oral work), group, individual work (independent work), work in pairs (mutual questioning).

Equipment and main sources of information:

Computer, projector, screen, presentation for the lesson on the topic “Methods of solving quadratic equations.”

Performance sheet for control and self-control.

Cards-tasks for multi-level independent work

Technological map of the lesson:

Activity

student

Organizational

Greeting students

Teacher's greeting

Setting the goals and objectives of the lesson. Motivation for students' learning activities

At the final certification, there are often tasks where you need to be able to solve quadratic equations.

Communicating the purpose of the lesson :

Today in the lesson we will repeat, generalize, and bring into the system the studied types, methods and techniques for solving quadratic equations.

Based on the results of their work, that is, according to the number of points scored, everyone will receive grades.

Lesson motto: “We think, think, work and help each other”

(Slide 2 ).

The teachers are listening.

Updating knowledge.

Guys, we usually start the lesson by checking our homework.

Who will say that it was necessary to repeat about quadratic equations?

What are quadratic equations?

What are they?

What methods of solving quadratic equations do you know?

Teachers answer questions and conduct a self-assessment of their knowledge.

Generalization and systematization of knowledge

1. Mutual control role.

Here are the equations (slide 3)

x 2 + 7 x – 18 = 0;

2 x 2 + 1 = 0;

x 2 –2 x + 9 = 0;

2 y 2 – 3y + 1 = 0;

2 y 2 = 1;

–2 x 2 – x + 1 = 0;

x 2 + 6 x = 0;

4x 2 =0;

– x 2 – 6 x=1

2 x + x 2 – 1=0

On your table there is a card with questions that you need to answer (Appendix 1).

(slide 4 ) Checking the results, exchange cards with your neighbor.

Answer questions

2. Frontal work with the class.

On(slide 5) formulas with missing elements are written. The task of the class is to find out what this formula is and what is missing in the recording of this formula.

D = b ² – * a * .

D > 0 , means * root.

D * 0 , means 1 root.

D * 0 , Means * roots.

Answer questions

correct knowledge.

Solve equations from flashcards. One of the group members will show the solution on the board.

Compare your answers with the correct ones, for each correct answer - 1 point

Solve equations

Explain the solution.

Frontal work with the class

Tell me, could you immediately, without making calculations, answer my question: “What is the sum and product of the roots of a quadratic equation?” (One person at the blackboard writes down the formulas of Vieta’s theorem.)

(slide6)

Next task: verbally find the sum and difference of the roots of the equation using the theorem:

(answers: 5 and 6; 9 and 20; -3 and 2) Introduction to the method of solving some quadratic equations orally.

Vieta's theorem is widely used in equations of the formaX 2 + bx + c = 0.

The use of certain properties provides significant advantages for quickly obtaining answers when solving quadratic equations.

Let's consider these properties(slide7)

1) a + b+c = 0 x 1 = 1, x 2 = s/a.

5x 2 + 4x – 9 = 0; X 1 =1, x 2 = - 9/2.

2) a -b+ c = 0 x 1 = - 1, x 2 = - s/a.

For example: 4x 2 + 11x + 7 = 0; X 1 = - 1, x 2 = - 7/4.

(slide8)

3) a in +c 0

Solve the equation orally: x 2 + bx + ac = 0

Divide its roots by a.

a) 2x 2 – 11x + 5 = 0.

We solve the equation orally: x 2 – 11x + 10 = 0. Its roots are 1 and 10. Divide by 2.

Then x 1 = , x 2 = 5.

Answer: ; 5.

(slide9)

c) 6x 2 –7х – 3 = 0

We solve the equation orally: x 2 –7x – 18 = 0. Its roots are -2 and 9. Divide by 6.

Then x 1 = - , x 2 = .

Answer: -; .

Answer questions. Fill knowledge gaps

Work in multi-level groups

Reception "Compliance"

“Catch a mistake” technique

Solve equations using these properties(slide 10)

Igroup.

1)find the sum of the roots of the equation

2x 2 – 3x + 1 = 0

2) Find the product of the roots of the equation

X 2 +9x +20 = 0

3) solve the equation

10x 2 – 8x - 2= 0

IIgroup.

1)find the sum and product of the roots of the equation

3x 2 – 8x + 5 = 0

Solve equations

2)x 2 + 2x -24 = 0

3)2 x 2 -7x +5 = 0

IIIgroup

Solve the problems:

1)x 2 +5x-6=0

2)5x 2 -7x+2=0

3)100x 2 -99x-199=0

Solve equations

Check the solution.

Correction of knowledge is carried out.

2. Match quadratic equations and methods for solving them:

(slide 11)

2x 2 – 3x + 11 = 0

7 x 2 = 8x

X 2 – 10x + 100 = 0

X 2 –5x –6 = 0

– 2x 2 + x +14= 0

-factorization

- general formula of roots

-Vieta's theorem

3. Find errors in solving equations =

Guys who complete the work quickly can solve an additional task(slide 14), written on the board.

After execution, a quick check is carried out.(slide15)

Now count the total number of points and give yourself a grade.(slide16)

30-24 points – score 5;

23-18 points – score 4;

12-17 points –. score4

And everyone is given a grade by the teacher for activity, courage, and perseverance. Well, if someone today failed to score points for a positive assessment, then success is still ahead of you, and it will definitely be with you next time.

Solve equations

conduct self-assessment.

Reflection.

Who can say what we repeated in class today?

Did you like how we did it?

Continue the phrases:

Now I know for sure...

I understand …

I learned …

My opinion …

Everyone has colored cards on the table.

If you are happy and satisfied with the lesson, raise a green card.

If the lesson is interesting and you worked actively, you raise a yellow card.

conduct self-assessment.

Homework

(slide 17) Solve equations from the collection of tasks

State final certification

9th grade graduates.

A.V. Semenov, A.S. Trepalin, I.V. Yashchenko

by level

Select tasks according to your level

Analysis of task No. 4 on the topic: "Solving equations of various types"

Additional materials
Dear users, do not forget to leave your comments, reviews, wishes! All materials have been checked by an anti-virus program.

Educational aids and simulators in the Integral online store for grade 9
Interactive manual "Rules and exercises in algebra" for grade 9
Multimedia textbook for grade 9 "Algebra in 10 minutes"

Task No. 4 requires the ability to solve equations of various types. Guys, you should be well versed in the methods of correctly solving quadratic equations, fractional rational equations, and ordinary linear equations. You should also be good at performing operations with polynomials: multiplying and dividing a polynomial by a polynomial. Do you need the ability to select the roots of an equation that are included in the solution area and determine which roots should be thrown out and not taken into account?

Lessons that will help you in preparing this assignment:

1.Basic definitions and examples of solutions of linear functions.
2. Concept and standard form of a monomial.
3. Polynomial, standard form, reduction, transformation.
4. Examples for numerical expressions. Algebraic expressions with variables and operations with them.
5. Equations, examples of solving equations.
6. Quadratic equations. Lesson in progress.
7. Fractional rational equations. Lesson in progress.
8. Square root. Lesson in progress.

Let's move on to analyzing examples of solutions.

Example 1.
Find the roots of the equation: $16x^2-1=0$.

Solution.
Note that we are given a quadratic equation, but not a complete one. The coefficient of x is zero. Then we will be guided by the rule: “we will leave those expressions in which there is x squared on the left, and move all the numbers to the right.”
Let's transform our expression: $16x^2=1$.

Let's divide both sides of the equation by the coefficient of x squared: $x^2=\frac(1)(16)$.

To solve this equation, we need knowledge of the square root. Let's extract the root, not forgetting that we must also take into account the negative number: $x=±\sqrt(\frac(1)(16))=±\frac(1)(4)=±0.25$.
Answer: $x=±0.25$.

Example 2.
Solve the equation: $x^2=18-7x$.

Solution.
Let's move all the expressions to the left side of the equation: $x^2+7x-18=0$.

We can solve the usual quadratic equation in two ways:
1. “head-on”, calculating the discriminant;
2. using Viette's theorem.

1 way.
Let's write down all the coefficients for the quadratic equation: $a=1$, $b=7$, $c=-18$.

Let's find the discriminant: $D=b^2-4ac=(7)^2-4*1*(-18)=49+72=121=(11)^2>0$.
We found that the equation has 2 roots.
We just have to find these roots:
$x_1=\frac(-b+\sqrt(D))(2a)=\frac(-7+11)(2)=2$.
$x_2=\frac(-b-\sqrt(D))(2a)=\frac(-7-11)(2)=-9$.

Method 2.
Let's use Viette's theorem. Viette's theorem often simplifies the solution of quadratic equations many times, especially when the coefficient $a=1$. In this case, the product of the roots of the equation is equal to the coefficient $c$, and the sum of the roots of the equation is equal to minus the coefficient of $b$:
$x_1+x_2=-\frac(b)(a)$.
$x_1*x_2=\frac(c)(a)$.

In our example, $с=-18$ and $b=7$. We begin to sort through pairs of numbers whose product is equal to minus eighteen. The first numbers that come to mind are nine and two. After performing a few simple multiplications and additions, we can verify that the roots $x=-9$ and $x=2$ are suitable for us.
$x_1*x_2=-9*2=-18=\frac(c)(a)$.
x$_1+x_2=-9+2=-7=-\frac(b)(a)$.
Answer: $x=-9$, $x=2$.

Example 3.
Solve the equation: $x-\frac(x)(7)=\frac(15)(7)$.

Solution.
We are given an ordinary linear equation with fractional coefficients. To solve this equation you need to work correctly with ordinary fractions.
The first step is to transform the left side of the equation, simplifying it: $x-\frac(x)(7)=\frac(7x)(7)-\frac(x)(7)=\frac(6x)(7)$.
We got the equation: $\frac(6x)(7)=\frac(15)(7)$.
Let's divide the right side of the equation by the coefficient of x: $x=\frac(\frac(15)(7))(\frac(6)(7))$.

Let's consider division separately: $\frac(\frac(15)(7))(\frac(6)(7))=\frac(15)(7)*\frac(7)(6)=\frac(15 )(6)=2\frac(3)(6)=2\frac(1)(2)=$2.5.

We received: $x=2.5$.
Answer: $x=2.5$.

Example 4.
Solve the equation: $(x+2)^2=(x-4)^2$.

Solution.
Method 1.
Let's use the formula for the square of the sum: $(x+2)^2=x^2+4x+4$.
$(x-4)^2=x^2-8x+16$.
We received: $x^2+4x+4=x^2-8x+16$.
Let's simplify our equation:
$x^2+4x-x^2+8x=16-4$.
$12x=$12.
$x=1$.

Method 2.
To solve this equation, we can use the difference of squares formula. $(x+2)^2-(x-4)^2=0$.
$(x+2+x-4)(x+2-x+4)=0$.
$(2x-2)*(6)=0$.
$2x-2=0$.
$2x=2$.
$x=1$.
Answer: $x=1$.

Example 5.
Solve the equation: $\frac(9)(x-14)=\frac(14)(x-9)$.

Solution.
We are presented with a fractional rational equation. When solving these equations, it is worth remembering that you cannot divide by zero. Therefore, the roots of the equation should always be checked by substituting them into the denominator of the original equation.
Let's use the cross-by-cross multiplication rule: $9(x-9)=14(x-14)$.
We got a linear equation:
$9x-81=14x-196$.
$9x-14x=-196+81$.
$-5x=-115$.
$x=23$.
Having checked our root, we are convinced that the denominators of the fractions of the original equation do not vanish.
Answer: $x=23$.

Example 6.
Find solutions that satisfy the system: $\begin (cases) x^2+9x-22=0, \\ x≤1 \end (cases)$.

Solution.
First, let's solve the quadratic equation using Viette's theorem. The product of our roots is $22$, and the sum is $-9$.
Let's select the roots:
$-11*2=-22$.
$-11+2=-9$.
We got two roots: $x_1=-11$ and $x_2=2$. Of these roots, the inequality $x≤1$ is satisfied by the first root, and it will be the answer.
Answer: $x=-11$.

Example 7.
Solve the equation: $23x-60-x^2=0$.
In your answer, indicate the modulus of the difference of the roots.

Solution.
Let's multiply the original equation by $-1$: $x^2-23x+60=0$.
In this form, the equation looks much more familiar.
Let's use Viette's theorem and present our equation as a product of binomials:
$(x-20)(x-3)=0$.
We got two roots $x_1=20$ and $x_2=3$.
Let's find the difference modulus: $|x_1-x_2|=|20-3|=|17|=17$.
Answer: 17.

Example 8.
How many roots does the equation $x^6-x^2=0 have?$

Solution.
Let's take the smallest degree out of brackets: $x^2(x^4-1)=0$.
Now let's use the difference of squares formula:
$x^2 (x^2-1)(x^2+1)=0$.
And let's use the same formula again:
$x^2 (x-1)(x+1)(x^2+1)=0$.
This equation is equivalent to a set of equations: We found that this equation has three roots.
Answer: 3.

Example 9.
Solve the equation: $\frac((x-2)(2x+1))(2-x)=0$.
If the equation has more than one root, write down the larger one as your answer.

Solution.
The original equation is equivalent to the following set: Let's solve each equation: Since the denominator of the fraction cannot be equal to zero, one solution is eliminated. We got one root of the equation $x=-0.5$.
Answer: -0.5.

Alexander Shabalin

! From theory to practice;

! From simple to complex

MAOU "Platoshin Secondary School",

mathematics teacher, Melekhina G.V.

General form of a linear equation: ax + b = 0 ,

Where a And b– numbers (coefficients).

If a = 0 And b = 0, That 0x + 0 = 0 – infinitely many roots;
If a = 0 And b ≠ 0, That 0x + b = 0– no solutions;
If a ≠ 0 And b = 0 , That ax + 0 = 0 – one root, x = 0;
If a ≠ 0 And b ≠ 0 , That ax + b = 0 – one root,

! If X is to the first power and is not in the denominator, then it is a linear equation

! And if the linear equation is complex :

! The terms with X go to the left, without X - to the right.

! These equations are also linear .

! The main property of proportion (crosswise).

! Open the brackets, with X to the left, without X to the right.

if the coefficient a = 1, then the equation is called given :

if the coefficient b = 0 or/and c = 0, then the equation is called incomplete :

! Basic formulas

! More formulas

Biquadratic equation- called an equation of the form ax 4 +bx 2 + c = 0 .

The biquadratic equation reduces to quadratic equation using substitution, then

We get a quadratic equation:

Let's find the roots and return to the replacement:

Example 1:

Solve equation x 4 + 5x 2 – 36 = 0.

Solution:

Substitution: x 2 = t.

t 2 + 5t – 36 = 0. The roots of the equation are t 1 = -9 and t 2 = 4.

x 2 = -9 or x 2 = 4.

Answer: There are no roots in the first equation, but in the second: x = ±2.

Example 2:

Solve the equation (2x – 1) 4 – 25(2x – 1) 2 + 144 = 0.

Solution:

Substitution: (2x – 1) 2 = t.

t 2 – 25t + 144 = 0. The roots of the equation are t 1 = 9 and t 2 = 16.

(2x – 1) 2 = 9 or (2x – 1) 2 = 16.

2x – 1 = ±3 or 2x – 1 = ±4.

The first equation has two roots: x = 2 and x = -1, the second also has two roots: x = 2.5 and x = -1.5.

Answer: -1.5; -1; 2; 2.5.

1) X 4 - 9 X 2 = 0; 2) 4 X 4 - x 2 = 0;

1) X 4 + x 2 - 2 = 0;

2) X 4 - 3 X 2 - 4 = 0; 3) 9 X 4 + 8 X 2 - 1 = 0; 4) 20 X 4 - X 2 - 1 = 0.

Solve equations by selecting from the left side full square :

1) X 4 - 20 X 2 + 64 = 0; 2) X 4 - 13 X 2 + 36 = 0; 3) X 4 - 4 X 2 + 1 = 0; 4) X 4 + 2 X 2 +1 = 0.

! Remember the square of the sum and the square of the difference

Rational expression is an algebraic expression made up of numbers and a variable x using the operations of addition, subtraction, multiplication, division and exponentiation with a natural exponent.

If r(x) is a rational expression, then the equation r(x)=0 called a rational equation.

Algorithm for solving a rational equation:

1. Move all terms of the equation into one side.

2. Convert this part of the equation to an algebraic fraction p(x)/q(x)

3. Solve the equation p(x)=0

4. For each root of the equation p(x)=0 check whether it satisfies the condition q(x)≠0 or not. If yes, then this is the root of the given equation; if not, then it is an extraneous root and should not be included in the answer.

! Let us recall the solution to the fractional rational equation:

! To solve equations, it is useful to recall the abbreviated multiplication formulas:

If an equation contains a variable under the square root sign, then the equation is called irrational .

Method of squaring both sides of an equation- the main method for solving irrational equations.

Having solved the resulting rational equation, it is necessary to check , weeding out possible extraneous roots.

Answer: 5; 4

Another example:

Examination:

The expression has no meaning.

Answer: no solutions.

In the term “quadratic equation,” the key word is “quadratic.” This means that the equation must necessarily contain a variable (that same x) squared, and there should not be xes to the third (or greater) power.

The solution of many equations comes down to solving quadratic equations.

Let's learn to determine that this is a quadratic equation and not some other equation.

Example 1.

Let's get rid of the denominator and multiply each term of the equation by

Let's move everything to the left side and arrange the terms in descending order of powers of X

Now we can say with confidence that this equation is quadratic!

Example 2.

Multiply the left and right sides by:

This equation, although it was originally in it, is not quadratic!

Example 3.

Let's multiply everything by:

Scary? The fourth and second degrees... However, if we make a replacement, we will see that we have a simple quadratic equation:

Example 4.

It seems to be there, but let's take a closer look. Let's move everything to the left side:

See, it's reduced - and now it's a simple linear equation!

Now try to determine for yourself which of the following equations are quadratic and which are not:

Examples:

Answers:

square;
square;
not square;
not square;
not square;
square;
not square;
square.

Mathematicians conventionally divide all quadratic equations into the following types:

Complete quadratic equations- equations in which the coefficients and, as well as the free term c, are not equal to zero (as in the example). In addition, among complete quadratic equations there are given- these are equations in which the coefficient (the equation from example one is not only complete, but also reduced!)

Incomplete quadratic equations- equations in which the coefficient and or the free term c are equal to zero:
They are incomplete because they are missing some element. But the equation must always contain x squared!!! Otherwise, it will no longer be a quadratic equation, but some other equation.

Why did they come up with such a division? It would seem that there is an X squared, and okay. This division is determined by the solution methods. Let's look at each of them in more detail.

Solving incomplete quadratic equations

First, let's focus on solving incomplete quadratic equations - they are much simpler!

There are types of incomplete quadratic equations:

, in this equation the coefficient is equal.
, in this equation the free term is equal to.
, in this equation the coefficient and the free term are equal.

1. i. Since we know how to take the square root, let's express from this equation

The expression can be either negative or positive. A squared number cannot be negative, because when multiplying two negative or two positive numbers, the result will always be a positive number, so: if, then the equation has no solutions.

And if, then we get two roots. There is no need to memorize these formulas. The main thing is that you must know and always remember that it cannot be less.

Let's try to solve some examples.

Example 5:

Solve the equation

Now all that remains is to extract the root from the left and right sides. After all, you remember how to extract roots?

Answer:

Never forget about roots with a negative sign!!!

Example 6:

Solve the equation

Answer:

Example 7:

Solve the equation

Oh! The square of a number cannot be negative, which means that the equation

no roots!

For such equations that have no roots, mathematicians came up with a special icon - (empty set). And the answer can be written like this:

Answer:

Thus, this quadratic equation has two roots. There are no restrictions here, since we did not extract the root.
Example 8:

Solve the equation

Let's take the common factor out of brackets:

Thus,

This equation has two roots.

Answer:

The simplest type of incomplete quadratic equations (although they are all simple, right?). Obviously, this equation always has only one root:

We will dispense with examples here.

Solving complete quadratic equations

We remind you that a complete quadratic equation is an equation of the form equation where

Solving complete quadratic equations is a little more difficult (just a little) than these.

Remember, Any quadratic equation can be solved using a discriminant! Even incomplete.

The other methods will help you do it faster, but if you have problems with quadratic equations, first master the solution using the discriminant.

1. Solving quadratic equations using a discriminant.

Solving quadratic equations using this method is very simple; the main thing is to remember the sequence of actions and a couple of formulas.

If, then the equation has a root. You need to pay special attention to the step. Discriminant () tells us the number of roots of the equation.

If, then the formula in the step will be reduced to. Thus, the equation will only have a root.
If, then we will not be able to extract the root of the discriminant at the step. This indicates that the equation has no roots.

Let's go back to our equations and look at some examples.

Example 9:

Solve the equation

Step 1 we skip.

Step 2.

We find the discriminant:

This means the equation has two roots.

Step 3.

Answer:

Example 10:

Solve the equation

The equation is presented in standard form, so Step 1 we skip.

Step 2.

We find the discriminant:

This means that the equation has one root.

Answer:

Example 11:

Solve the equation

The equation is presented in standard form, so Step 1 we skip.

Step 2.

We find the discriminant:

This means we will not be able to extract the root of the discriminant. There are no roots of the equation.

Now we know how to correctly write down such answers.

Answer: no roots

2. Solving quadratic equations using Vieta's theorem.

If you remember, there is a type of equation that is called reduced (when the coefficient a is equal to):

Such equations are very easy to solve using Vieta’s theorem:

Sum of roots given quadratic equation is equal, and the product of the roots is equal.

Example 12:

Solve the equation

This equation can be solved using Vieta's theorem because .

The sum of the roots of the equation is equal, i.e. we get the first equation:

And the product is equal to:

Let's compose and solve the system:

And. The amount is equal to;
And. The amount is equal to;
And. The amount is equal.

and are the solution to the system:

Answer: ; .

Example 13:

Solve the equation

Answer:

Example 14:

Solve the equation

The equation is given, which means:

Answer:

QUADRATIC EQUATIONS. AVERAGE LEVEL

What is a quadratic equation?

In other words, a quadratic equation is an equation of the form, where - the unknown, - some numbers, and.

The number is called the highest or first coefficient quadratic equation, - second coefficient, A - free member.

Why? Because if the equation immediately becomes linear, because will disappear.

In this case, and can be equal to zero. In this chair equation is called incomplete. If all the terms are in place, that is, the equation is complete.

Solutions to various types of quadratic equations

Methods for solving incomplete quadratic equations:

First, let's look at methods for solving incomplete quadratic equations - they are simpler.

We can distinguish the following types of equations:

I., in this equation the coefficient and the free term are equal.

II. , in this equation the coefficient is equal.

III. , in this equation the free term is equal to.

Now let's look at the solution to each of these subtypes.

Obviously, this equation always has only one root:

A squared number cannot be negative, because when you multiply two negative or two positive numbers, the result will always be a positive number. That's why:

if, then the equation has no solutions;

if we have two roots

There is no need to memorize these formulas. The main thing to remember is that it cannot be less.

Examples:

Solutions:

Answer:

Never forget about roots with a negative sign!

The square of a number cannot be negative, which means that the equation

no roots.

To briefly write down that a problem has no solutions, we use the empty set icon.

Answer:

So, this equation has two roots: and.

Answer:

Let's take the common factor out of brackets:

The product is equal to zero if at least one of the factors is equal to zero. This means that the equation has a solution when:

So, this quadratic equation has two roots: and.

Example:

Solve the equation.

Solution:

Let's factor the left side of the equation and find the roots:

Answer:

Methods for solving complete quadratic equations:

1. Discriminant

Solving quadratic equations this way is easy, the main thing is to remember the sequence of actions and a couple of formulas. Remember, any quadratic equation can be solved using a discriminant! Even incomplete.

Did you notice the root from the discriminant in the formula for roots? But the discriminant can be negative. What to do? We need to pay special attention to step 2. The discriminant tells us the number of roots of the equation.

If, then the equation has roots:
If, then the equation has the same roots, and in fact, one root:
Such roots are called double roots.
If, then the root of the discriminant is not extracted. This indicates that the equation has no roots.

Why are different numbers of roots possible? Let us turn to the geometric meaning of the quadratic equation. The graph of the function is a parabola:

In a special case, which is a quadratic equation, . This means that the roots of a quadratic equation are the points of intersection with the abscissa axis (axis). A parabola may not intersect the axis at all, or may intersect it at one (when the vertex of the parabola lies on the axis) or two points.

In addition, the coefficient is responsible for the direction of the branches of the parabola. If, then the branches of the parabola are directed upward, and if, then downward.

Examples:

Solutions:

Answer:

Answer: .

Answer:

This means there are no solutions.

Answer: .

2. Vieta's theorem

It is very easy to use Vieta's theorem: you just need to choose a pair of numbers whose product is equal to the free term of the equation, and the sum is equal to the second coefficient taken with the opposite sign.

It is important to remember that Vieta's theorem can only be applied in reduced quadratic equations ().

Let's look at a few examples:

Example #1:

Solve the equation.

Solution:

This equation can be solved using Vieta's theorem because . Other coefficients: ; .

The sum of the roots of the equation is:

And the product is equal to:

Let's select pairs of numbers whose product is equal and check whether their sum is equal:

And. The amount is equal to;
And. The amount is equal to;
And. The amount is equal.

and are the solution to the system:

Thus, and are the roots of our equation.

Answer: ; .

Example #2:

Solution:

Let's select pairs of numbers that give in the product, and then check whether their sum is equal:

and: they give in total.

and: they give in total. To obtain, it is enough to simply change the signs of the supposed roots: and, after all, the product.

Answer:

Example #3:

Solution:

The free term of the equation is negative, and therefore the product of the roots is a negative number. This is only possible if one of the roots is negative and the other is positive. Therefore the sum of the roots is equal to differences of their modules.

Let us select pairs of numbers that give in the product, and whose difference is equal to:

and: their difference is equal - does not fit;

and: - not suitable;

and: - suitable. All that remains is to remember that one of the roots is negative. Since their sum must be equal, the root with the smaller modulus must be negative: . We check:

Answer:

Example #4:

Solve the equation.

Solution:

The equation is given, which means:

The free term is negative, and therefore the product of the roots is negative. And this is only possible when one root of the equation is negative and the other is positive.

Let's select pairs of numbers whose product is equal, and then determine which roots should have a negative sign:

Obviously, only the roots and are suitable for the first condition:

Answer:

Example #5:

Solve the equation.

Solution:

The equation is given, which means:

The sum of the roots is negative, which means that at least one of the roots is negative. But since their product is positive, it means both roots have a minus sign.

Let us select pairs of numbers whose product is equal to:

Obviously, the roots are the numbers and.

Answer:

Agree, it’s very convenient to come up with roots orally, instead of counting this nasty discriminant. Try to use Vieta's theorem as often as possible.

But Vieta’s theorem is needed in order to facilitate and speed up finding the roots. In order for you to benefit from using it, you must bring the actions to automaticity. And for this, solve five more examples. But don't cheat: you can't use a discriminant! Only Vieta's theorem:

Solutions to tasks for independent work:

Task 1. ((x)^(2))-8x+12=0

According to Vieta's theorem:

As usual, we start the selection with the piece:

Not suitable because the amount;

: the amount is just what you need.

Answer: ; .

Task 2.

And again our favorite Vieta theorem: the sum must be equal, and the product must be equal.

But since it must be not, but, we change the signs of the roots: and (in total).

Answer: ; .

Task 3.

Hmm... Where is that?

You need to move all the terms into one part:

The sum of the roots is equal to the product.

Okay, stop! The equation is not given. But Vieta's theorem is applicable only in the given equations. So first you need to give an equation. If you can’t lead, give up this idea and solve it in another way (for example, through a discriminant). Let me remind you that to give a quadratic equation means to make the leading coefficient equal:

Great. Then the sum of the roots is equal to and the product.

Here it’s as easy as shelling pears to choose: after all, it’s a prime number (sorry for the tautology).

Answer: ; .

Task 4.

The free member is negative. What's special about this? And the fact is that the roots will have different signs. And now, during the selection, we check not the sum of the roots, but the difference in their modules: this difference is equal, but a product.

So, the roots are equal to and, but one of them is minus. Vieta's theorem tells us that the sum of the roots is equal to the second coefficient with the opposite sign, that is. This means that the smaller root will have a minus: and, since.

Answer: ; .

Task 5.

What should you do first? That's right, give the equation:

Again: we select the factors of the number, and their difference should be equal to:

The roots are equal to and, but one of them is minus. Which? Their sum should be equal, which means that the minus will have a larger root.

Answer: ; .

Let me summarize:

Vieta's theorem is used only in the quadratic equations given.
Using Vieta's theorem, you can find the roots by selection, orally.
If the equation is not given or no suitable pair of factors of the free term is found, then there are no whole roots, and you need to solve it in another way (for example, through a discriminant).

3. Method for selecting a complete square

If all terms containing the unknown are represented in the form of terms from abbreviated multiplication formulas - the square of the sum or difference - then after replacing variables, the equation can be presented in the form of an incomplete quadratic equation of the type.

For example:

Example 1:

Solve the equation: .

Solution:

Answer:

Example 2:

Solve the equation: .

Solution:

Answer:

In general, the transformation will look like this:

This implies: .

Doesn't remind you of anything? This is a discriminatory thing! That's exactly how we got the discriminant formula.

QUADRATIC EQUATIONS. BRIEFLY ABOUT THE MAIN THINGS

Quadratic equation- this is an equation of the form, where - the unknown, - the coefficients of the quadratic equation, - the free term.

Complete quadratic equation- an equation in which the coefficients are not equal to zero.

Reduced quadratic equation- an equation in which the coefficient, that is: .

Incomplete quadratic equation- an equation in which the coefficient and or the free term c are equal to zero:

if the coefficient, the equation looks like: ,
if there is a free term, the equation has the form: ,
if and, the equation looks like: .

1. Algorithm for solving incomplete quadratic equations

1.1. An incomplete quadratic equation of the form, where, :

1) Let's express the unknown: ,

2) Check the sign of the expression:

if, then the equation has no solutions,
if, then the equation has two roots.

1.2. An incomplete quadratic equation of the form, where, :

1) Let’s take the common factor out of brackets: ,

2) The product is equal to zero if at least one of the factors is equal to zero. Therefore, the equation has two roots:

1.3. An incomplete quadratic equation of the form, where:

This equation always has only one root: .

2. Algorithm for solving complete quadratic equations of the form where

2.1. Solution using discriminant

1) Let's bring the equation to standard form: ,

2) Let's calculate the discriminant using the formula: , which indicates the number of roots of the equation:

3) Find the roots of the equation:

if, then the equation has roots, which are found by the formula:
if, then the equation has a root, which is found by the formula:
if, then the equation has no roots.

2.2. Solution using Vieta's theorem

The sum of the roots of the reduced quadratic equation (equation of the form where) is equal, and the product of the roots is equal, i.e. , A.

2.3. Solution by the method of selecting a complete square

If a quadratic equation of the form has roots, then it can be written in the form: .

Well, the topic is over. If you are reading these lines, it means you are very cool.

Because only 5% of people are able to master something on their own. And if you read to the end, then you are in this 5%!

Now the most important thing.

You have understood the theory on this topic. And, I repeat, this... this is just super! You are already better than the vast majority of your peers.

The problem is that this may not be enough...

For what?

For successfully passing the Unified State Exam, for entering college on a budget and, MOST IMPORTANTLY, for life.

I won’t convince you of anything, I’ll just say one thing...

People who have received a good education earn much more than those who have not received it. This is statistics.

But this is not the main thing.

The main thing is that they are MORE HAPPY (there are such studies). Perhaps because many more opportunities open up before them and life becomes brighter? Don't know...

But think for yourself...

What does it take to be sure to be better than others on the Unified State Exam and ultimately be... happier?

GAIN YOUR HAND BY SOLVING PROBLEMS ON THIS TOPIC.

You won't be asked for theory during the exam.

You will need solve problems against time.

And, if you haven’t solved them (A LOT!), you’ll definitely make a stupid mistake somewhere or simply won’t have time.

It's like in sports - you need to repeat it many times to win for sure.

Find the collection wherever you want, necessarily with solutions, detailed analysis and decide, decide, decide!

You can use our tasks (optional) and we, of course, recommend them.

In order to get better at using our tasks, you need to help extend the life of the YouClever textbook you are currently reading.

How? There are two options: