Acoustics is a field of physics that studies elastic vibrations and waves from the lowest frequencies to the extremely high (10 12 -10 13 Hz). Modern acoustics covers a wide range of issues; it includes a number of sections: physical acoustics, which studies the characteristics of the propagation of elastic waves in various media, physiological acoustics, which studies the structure and operation of sound-receiving and sound-producing organs in humans and animals, etc. In the narrow sense of the word, under Acoustics understands the study of sound, i.e. about elastic vibrations and waves in gases, liquids and solids perceived by the human ear (frequencies from 16 to 20,000 Hz).

8.1. NATURE OF SOUND. PHYSICAL CHARACTERISTICS

Sound vibrations and waves are a special case of mechanical vibrations and waves. However, due to the importance of acoustic concepts for assessing auditory sensations, as well as in connection with medical applications, it is advisable to examine some issues specifically. It is customary to distinguish the following sounds:

1) tones, or musical sounds;

2) noise;

3) sonic booms.

It's called a tonesound,which is a periodic process. If this process is harmonic, then the tone is called simple or clean, and the corresponding plane sound wave is described by equation (7.45). The main physical characteristic of a pure tone is frequency. Anharmonic 1 corresponds to fluctuation difficult tone. A simple tone is produced, for example, by a tuning fork, a complex tone is created by musical instruments, the apparatus of speech (vowel sounds), etc.

A complex tone can be broken down into simple ones. The lowest frequency ν ο of such an expansion corresponds to basic tone other harmonics (overtones) have frequencies equal to 2ν ο, 3ν ο, etc. A set of frequencies indicating their relative intensity (amplitude A) called acoustically

1 Anharmonic - non-harmonic vibration.

sky spectrum(see 6.4). The complex tone spectrum is lined; in Fig. Figure 8.1 shows the acoustic spectra of the same note (ν 0 = 100 Hz), taken on the piano (a) and clarinet (b). Thus, the acoustic spectrum is an important physical characteristic of a complex tone.

Noise is a sound that has a complex, non-repeating time dependence.

Rice. 8.1

Noise includes sounds from vibration of machines, applause, noise of a burner flame, rustling, creaking, consonant sounds of speech, etc.

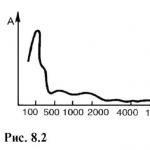
Noise can be thought of as a combination of randomly varying complex tones. If we try, with some degree of convention, to decompose the noise into a spectrum, it turns out that this spectrum will be continuous, for example, the spectrum obtained from the combustion noise of a Bunsen gas burner (Fig. 8.2).

A sonic boom is a short-term sound impact: bang, explosion, etc. A sonic boom should not be confused with a shock wave(see 7.10).

1 Strictly speaking, in this formula underR the average amplitude of sound pressure should be understood.

8.2. CHARACTERISTICS OF AUDITORY SENSATION. SOUND MEASUREMENTS

8.1 considered objective characteristics of sound that could be assessed by appropriate instruments independently of the individual. However, sound is an object of auditory sensations, and therefore is assessed by a person subjectively.

When perceiving tones, a person distinguishes them by pitch.

Height- a subjective characteristic determined primarily by the frequency of the fundamental tone.

To a much lesser extent, pitch depends on the complexity of the tone and its intensity: a sound of greater intensity is perceived as a sound of a lower tone.

Timbre sound is almost exclusively determined by its spectral composition.

In Fig. 8.1, different acoustic spectra correspond to different timbres, although the fundamental tone and therefore the pitch are the same.

Volume- another subjective assessment of sound, which characterizes the level of auditory sensation.

Although subjective, loudness can be quantified by comparing the auditory sensation of two sources.

The basis for creating a volume level scale is an important psychophysical law of Weber-Fechner: if you increase irritation in geometric progression (i.e. by the same number of times), then the sensation of this irritation increases in arithmetic progression (i.e. by the same amount).

In relation to sound, this means that if the sound intensity takes on a series of successive values, for example a1 0, a 2 1 0, and 3 1 0 (a is a certain coefficient, A>1), etc., then the corresponding sensations of sound volume E 0, 2E 0, 3E 0, etc.

Mathematically, this means that the loudness of a sound is proportional to the logarithm of the sound intensity.

If there are two sound stimuli with intensities I and I 0, and I 0 is the threshold of audibility, then, based on the Weber-Fechner law, the loudness relative to it is related to the intensities as follows:

E= klg(I/ I,), (8.3)

Where k- a certain proportionality coefficient depending on frequency and intensity.

If the coefficient k was constant, then from (8.1) and (8.3) it would follow that the logarithmic scale of sound intensities corresponds to the loudness scale. In this case, the loudness of the sound, as well as the intensity, would be expressed in bels or decibels. However, strong dependence k from the frequency and intensity of sound does not allow the measurement of loudness to be reduced to the simple use of formula (8.3).

Conventionally, it is assumed that at a frequency of 1 kHz the volume and intensity scales of sound completely coincide, i.e. k = 1 and E b = log(I/I 0), or, by analogy with (8.2):

E f = 10 log(I/l0). (8.4)

To distinguish it from the sound intensity scale in the loudness scale, decibels are called backgrounds(background).

Loudness at other frequencies can be measured by comparing the sound of interest to a sound at 1 kHz. To do this using sound generator 1 create a sound with a frequency of 1 kHz. The intensity of the sound is changed until an auditory sensation similar to the sensation of the volume of the sound being studied occurs. The intensity of a sound with a frequency of 1 kHz in decibels, measured by the device, is equal to the volume of this sound in the background.

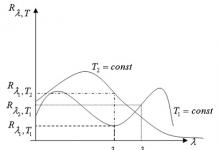
In order to find a correspondence between the volume and intensity of sound at different frequencies, use curves of equal loudness (Fig. 8.4). These curves are based on the average data obtained from people with normal hearing when measured using the method described above.

The lower curve corresponds to the intensities of the weakest audible sounds - the threshold of audibility; for all frequencies Eph = 0, for 1 kHz sound intensity I 0= 1 pW/m2. From the above curves it can be seen that the average human ear is most sensitive to frequencies of 2500-3000 Hz. Each intermediate curve corresponds to the same volume, but different sound intensity for different frequencies. Using a separate curve equal to loudness, one can find the intensities that, at certain frequencies, cause the sensation of this loudness. Using a set of curves of equal loudness, one can find for different

1 A sound generator is an electronic device that generates electrical vibrations at frequencies in the audio range. However, the sound generator itself is not the source of the sound. If the vibration it creates is applied to a speaker, then a sound appears, the tonality of which corresponds to the frequency of the generator. The sound generator provides the ability to smoothly change the amplitude and frequency of vibrations.

volume frequencies corresponding to a certain intensity. For example, let the intensity of a sound with a frequency of 100 Hz be 60 dB. What is the volume of this sound? In Fig. 8.2 we find a point with coordinates 100 Hz, 60 dB. It lies on the curve corresponding to a volume level of 30 von, which is the answer.

In order to have certain ideas about sounds of different natures, we present their physical characteristics (Table 8.1).

Table 8.1

The method for measuring hearing acuity is called audiometry. During audiometry on a special device (audiometer) determine the threshold of auditory sensation at different frequencies; the resulting curve is called audio diagram. Comparing the audiogram of a sick person with a normal auditory threshold curve helps diagnose hearing disease.

To objectively measure the noise volume level, it is used sound level meter Structurally, it corresponds to the diagram shown in Fig. 8.3. The properties of the sound level meter approach those of the human ear (see equal loudness curves in Fig. 8.4); for this purpose, corrective electrical filters are used for different ranges of loudness levels.

8.3. PHYSICAL BASES OF SOUND METHODS OF RESEARCH IN THE CLINIC

Sound, like light, is a source of information, and this is its main significance.

The sounds of nature, the speech of people around us, the noise of operating machines tell us a lot. To imagine the meaning of sound for a person, it is enough to temporarily deprive yourself of the ability to perceive sound - close your ears.

Naturally, sound can also be a source of information about the state of a person’s internal organs. Common sound method

diagnostics of diseases - auscultation(listening) - known since the 2nd century. BC. Used for auscultation stethoscope or phonendoscope. The phonendoscope (Fig. 8.5) consists of a hollow capsule 1 with a sound-transmitting membrane 2, applied to the patient’s body, rubber tubes coming from it 3 to the doctor's ear. A resonance of the air column occurs in the hollow capsule, as a result of which the sound intensifies and the au-cultation improves.

When auscultating the lungs, breathing sounds and various wheezing characteristic of diseases are heard. By changes in heart sounds and the appearance of murmurs, one can judge the state of cardiac activity. Using auscultation, you can determine the presence of peristalsis of the stomach and intestines and listen to the fetal heartbeat.

To simultaneously listen to a patient by several researchers for educational purposes or during a consultation, a system is used that includes a microphone, an amplifier and a loudspeaker or several telephones.

To diagnose the state of cardiac activity, a method similar to auscultation is used and is called phonocardiography(FKG). This method consists of graphically recording heart sounds and murmurs and their diagnostic interpretation. The phonocardiogram is recorded using a phonocardiograph (Fig. 8.6), consisting of a microphone, an amplifier, a system of frequency filters and a recording device. In Fig. Figure 8.7 shows a normal phonocardiogram.

Fundamentally different from the two sound methods outlined above is percussion. In this method, the sound of individual parts of the body is listened to by tapping them.

Let's imagine a closed cavity filled with air inside some body. If you induce sound vibrations in this body, then at a certain frequency of sound, the air in the cavity will begin to resonate, releasing and amplifying a tone corresponding to the size and position of the cavity.

Schematically, the human body can be represented as a set of gas-filled (lungs), liquid (internal organs) and solid (bone) volumes. When hitting the surface of a body, vibrations occur, the frequencies of which have a wide range. From this range, some vibrations will fade out quite quickly, while others, coinciding with the natural vibrations of the voids, will intensify and, due to resonance, will be audible. An experienced doctor determines the condition and topography of internal organs by the tone of percussion sounds.

8.4. WAVE RESISTANCE. REFLECTION OF SOUND WAVES. REVERBERATION

Sound pressure R depends on the speed υ of the oscillating particles of the medium. Calculations show that

Table 8.2

We use (8.8) to calculate the penetration coefficient of a sound wave from air into concrete and into water:

These data are impressive: it turns out that only a very small part of the energy of the sound wave passes from the air into concrete and into water. In any enclosed space, sound reflected from walls, ceilings, furniture falls on other walls, floors, etc., is again reflected and absorbed and gradually fades away. Therefore, even after the sound source stops, there are still sound waves in the room that create hum. This is especially noticeable in large spacious halls. The process of gradual attenuation of sound in enclosed spaces after the source is turned off is called reverberation.

Reverberation, on the one hand, is useful, since the perception of sound is enhanced by the energy of the reflected wave, but, on the other hand, excessively long reverberation can significantly worsen the perception of speech and music, since each new part of the text overlaps the previous ones. In this regard, they usually indicate some optimal reverberation time, which is taken into account when building auditoriums, theater and concert halls, etc. For example, the reverberation time of a filled Hall of Columns in the House of Unions in Moscow is 1.70 s, and a filled Bolshoi Theater is 1.55 s. For these rooms (empty), the reverberation time is 4.55 and 2.06 s, respectively.

8.5. PHYSICS OF HEARING

The auditory system connects the direct receiver of sound waves with the brain.

Using the concepts of cybernetics, we can say that the auditory system receives, processes and transmits information. From the entire auditory system, to consider the physics of hearing, we will single out the outer, middle and inner ears.

The outer ear consists of the auricle 1 and external auditory canal 2 (Fig. 8.8).

Rice. 8.9

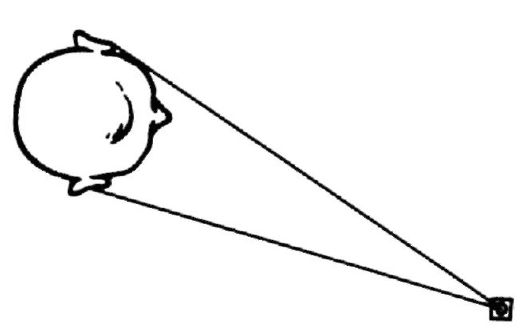
The auricle in humans does not play a significant role in hearing. It helps determine the localization of the sound source when it is located in the sagittal plane. Let's explain this. The sound from the source enters the ear. Depending on the position of the source in the vertical plane (Fig. 8.9), sound waves will diffract differently at the auricle due to its specific shape. This will also lead to different changes in the spectral composition of the sound wave entering the ear canal (diffraction issues are discussed in more detail in 24.6). As a result of experience, a person has learned to associate changes in the spectrum of a sound wave with the direction towards the sound source (directions A, B And IN in Fig. 8.9).

Possessing two sound receivers (ears), humans and animals are able to establish the direction to the sound source and in the horizontal plane (binaural effect; Fig. 8.10). This is explained by the fact that sound travels different distances from the source to different ears and a phase difference arises for the waves entering the right and left ears. The relationship between the difference in these distances (δ) and the phase difference (Δφ) is derived in 24.1 in explaining the interference of light [see (24.9)]. If the sound source is located directly in front of a person’s face, then δ = 0 and Δφ = 0; if the sound source is located on the side opposite one of the ears, then it will enter the other ear with a delay. Let us assume approximately that in this case δ is equal to the distance between the ears. Using formula (24.9), the phase difference can be calculated for ν = 1 kHz and δ = 0.15 m. It is approximately equal to 180°.

Different directions towards the sound source in the horizontal plane will correspond to a phase difference between 0° and 180° (for the above data). It is believed that a person with normal hearing can fix the direction of a sound source with an accuracy of 3°; this corresponds to a phase difference of 6°. Therefore, it can be assumed that people

Rice. 8.10

the eyelid is able to distinguish changes in the phase difference of sound waves entering its ears with an accuracy of 6°.

In addition to the phase difference, the binaural effect is facilitated by the difference in sound intensities in different ears, as well as the acoustic shadow from the head for one ear. In Fig. Figure 8.10 schematically shows that sound from a source enters the left ear as a result of diffraction.

The sound wave passes through the ear canal and is partially reflected from the eardrum 3. As a result of the interference of incident and reflected waves, acoustic resonance can occur. This occurs when the wavelength is four times the length of the external auditory canal. The length of the ear canal in humans is approximately 2.3 cm; therefore, acoustic resonance occurs at a frequency:

The most essential part of the middle ear is the eardrum 3 and auditory ossicles: hammer 4, incus 5 and stirrup 6 with corresponding muscles, tendons and ligaments. The bones transmit mechanical vibrations from the air environment of the outer ear to the liquid environment of the inner ear. The liquid medium of the inner ear has a characteristic impedance approximately equal to the characteristic impedance of water. As was shown (see 8.4), during the direct transition of a sound wave from air to water, only 0.122% of the incident intensity is transmitted. This is too little. Therefore, the main purpose of the middle ear is to help transmit greater sound intensity to the inner ear. Using technical language, we can say that the middle ear matches the wave resistance of the air and fluid of the inner ear.

The system of ossicles at one end is connected by a hammer to the eardrum (area S 1= 64 mm 2), on the other - a stirrup - with an oval window 7 inner ear (area S 2 = 3 mm 2).

Sound pressure p 1 acts on the eardrum, which determines the force

on 8, called vestibular staircase. Another channel comes from round window 9, it is called scala tympani 10. The vestibular and tympanic scala are connected in the area of ​​the cochlea's dome through a small opening - helicotrema 11. Thus, both of these canals in some way represent a single system filled with peri-lymph. Oscillations of the stapes 6 transmitted to the membrane of the oval window 7, from it to the perilymph and “bulge out” the membrane of the round window 9. The space between the scala vestibular and scala tympani is called cochlear canal 12, it is filled with endolymph. The main (basilar) membrane runs between the cochlear canal and the scala tympani along the cochlea. 13. It contains the organ of Corti, which contains receptor (hair) cells, and the auditory nerve extends from the cochlea (these details are not shown in Fig. 8.9).

The organ of Corti (spiral organ) converts mechanical vibrations into an electrical signal.

The length of the main membrane is about 32 mm, it widens and thins in the direction from the oval window at the apex of the cochlea (from a width of 0.1 to 0.5 mm). The main membrane is a very interesting structure for physics; it has frequency-selective properties. This was noticed by Helmholtz, who envisioned the main membrane as analogous to a series of tuned strings on a piano. Nobel laureate Bekesy established the fallacy of this resonator theory. Bekesy's work showed that the main membrane is a heterogeneous line of transmission of mechanical excitation. When exposed to an acoustic stimulus, a wave propagates along the main membrane. Depending on the frequency, this wave attenuates differently. The lower the frequency, the farther from the oval window the wave will travel along the main membrane before it begins to attenuate. For example, a wave with a frequency of 300 Hz will propagate to approximately 25 mm from the oval window before attenuation begins, and a wave with a frequency of 100 Hz reaches its maximum near 30 mm.

Based on these observations, theories were developed according to which the perception of pitch is determined by the position of the maximum vibration of the main membrane. Thus, a certain functional chain can be traced in the inner ear: oscillation of the oval window membrane - oscillation of the perilymph - complex oscillations of the main membrane - irritation of hair cells (receptors of the organ of Corti) - generation of an electrical signal.

Some forms of deafness are associated with damage to the receptor apparatus of the cochlea. In this case, the cochlea does not generate electrical signals.

nals when exposed to mechanical vibrations. Such deaf people can be helped by implanting electrodes into the cochlea and applying electrical signals to them corresponding to those that arise when exposed to a mechanical stimulus.

Such prosthetics for the main function of the cochlea (cochlear prosthetics) are being developed in a number of countries. In Russia, cochlear prosthetics was developed and implemented at the Russian Medical University. The cochlear prosthesis is shown in Fig. 8.12, here 1 - main body, 2 - earhook with microphone, 3 - electrical connector plug for connection to implantable electrodes.

8.6. ULTRASOUND AND BGO APPLICATIONS IN MEDICINE

Ultrasound(US) are mechanical vibrations and waves whose frequencies are more than 20 kHz.

The upper limit of ultrasonic frequencies can be considered to be 10 9 -10 10 Hz. This limit is determined by intermolecular distances and therefore depends on the state of aggregation of the substance in which the ultrasonic wave propagates.

To generate ultrasound, devices called ultrasound emitters are used. The most widespread are electromechanical emitters based on the phenomenon of the inverse piezoelectric effect (see 14.7). The reverse piezoelectric effect is

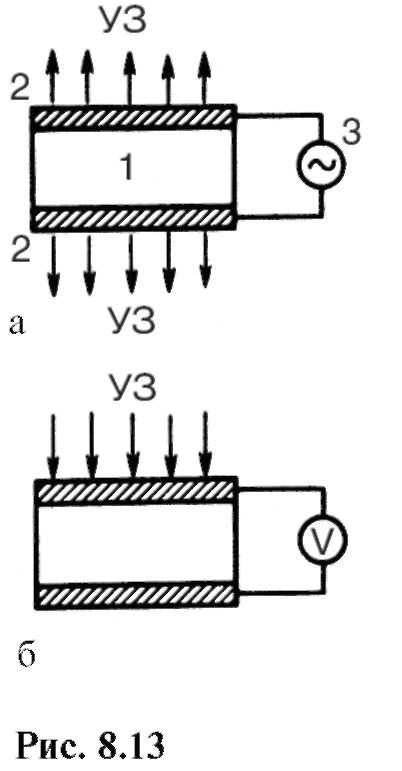
occurs in the mechanical deformation of bodies under the influence of an electric field. The main part of such an emitter (Fig. 8.13, a) is a plate or rod 1 made of a substance with well-pronounced piezoelectric properties (quartz, Rochelle salt, ceramic material based on barium titanate, etc.). Electrodes 2 are applied to the surface of the plate in the form of conductive layers. If an alternating electrical voltage from a generator is applied to the electrodes 3, then the plate, thanks to the inverse piezoelectric effect, will begin to vibrate, emitting a mechanical wave of the corresponding frequency.

The greatest effect of mechanical wave radiation occurs when the resonance condition is met (see 7.6). Thus, for plates 1 mm thick, resonance occurs for quartz at a frequency of 2.87 MHz, Rochelle salt - 1.5 MHz and barium titanate - 2.75 MHz.

An ultrasound receiver can be created based on the piezoelectric effect (direct piezoelectric effect). In this case, under the influence of a mechanical wave (ultrasonic wave), deformation of the crystal occurs (Fig. 8.13, b), which, with the piezoelectric effect, leads to the generation of an alternating electric field; the corresponding electrical voltage can be measured.

The use of ultrasound in medicine is associated with the peculiarities of its distribution and characteristic properties. Let's consider this question.

By its physical nature, ultrasound, like sound, is a mechanical (elastic) wave. However, the ultrasound wavelength is significantly less than the sound wavelength. For example, in water the wavelengths are 1.4 m (1 kHz, sound), 1.4 mm (1 MHz, ultrasound) and 1.4 μm (1 GHz, ultrasound). Wave diffraction (see 24.5) depends significantly on the ratio of the wavelength and the size of the bodies on which the wave diffracts. An “opaque” body measuring 1 m will not be an obstacle to a sound wave with a length of 1.4 m, but will become an obstacle to an ultrasound wave with a length of 1.4 mm, and an ultrasound shadow will appear. This makes it possible in some cases not to take into account the diffraction of ultrasonic waves, considering these waves as rays during refraction and reflection (similar to the refraction and reflection of light rays).

The reflection of ultrasound at the boundary of two media depends on the ratio of their wave impedances (see 8.4). Thus, ultrasound is well reflected at the muscle-periosteum-bone boundaries, on the surface of hollow organs, etc.

Therefore, it is possible to determine the location and size of inhomogeneous inclusions, cavities, internal organs, etc. (Ultrasonic location). Ultrasound location uses both continuous and pulsed radiation. In the first case, a standing wave is studied that arises from the interference of incident and reflected waves from the interface. In the second case, the reflected pulse is observed and the time of propagation of ultrasound to the object under study and back is measured. Knowing the speed of propagation of ultrasound, the depth of the object is determined.

The wave resistance of biological media is 3000 times greater than the wave resistance of air. Therefore, if an ultrasound emitter is applied to a human body, the ultrasound will not penetrate inside, but will be reflected due to a thin layer of air between the emitter and the biological object (see 8.4). To eliminate the air layer, the surface of the ultrasonic emitter is covered with a layer of oil.

The speed of propagation of ultrasonic waves and their absorption significantly depend on the state of the medium; This is the basis for the use of ultrasound to study the molecular properties of a substance. Research of this kind is the subject of molecular acoustics.

As can be seen from (7.53), the intensity of the wave is proportional to the square of the circular frequency, therefore it is possible to obtain ultrasonic waves of significant intensity even with a relatively small amplitude of oscillations. The acceleration of particles oscillating in an ultrasonic wave can also be large [see. (7.12)], which indicates the presence of significant forces acting on particles in biological tissues during ultrasound irradiation.

Compressions and rarefaction created by ultrasound lead to the formation of discontinuities in the continuity of the liquid - cavitations.

Cavitations do not last long and quickly collapse, while significant energy is released in small volumes, heating of the substance occurs, as well as ionization and dissociation of molecules.

Physical processes caused by the influence of ultrasound cause the following main effects in biological objects:

Microvibrations at the cellular and subcellular levels;

Destruction of biomacromolecules;

Restructuring and damage to biological membranes, changes in membrane permeability (see Chapter 13);

Thermal action;

Biomedical applications of ultrasound can mainly be divided into two areas: diagnostic and research methods and exposure methods.

The first direction includes location methods and the use of pulsed radiation. This echoencephalography- determination of tumors and cerebral edema (Fig. 8.14 shows echoencephalograph"Echo-12"); ultrasound cardiography- measurement of heart size in dynamics; in ophthalmology - ultrasonic location to determine the size of the ocular media. Using the Doppler ultrasound effect, the movement pattern of the heart valves is studied and the speed of blood flow is measured. For diagnostic purposes, the density of fused or damaged bone is determined by ultrasound speed.

The second direction concerns ultrasound physiotherapy. In Fig. Figure 8.15 shows the UTP-ZM apparatus used for these purposes. The patient is exposed to ultrasound using a special radiating head of the device. Usually, ultrasound with a frequency of 800 kHz is used for therapeutic purposes, its average intensity is about 1 W/cm 2 or less.

The primary mechanism of ultrasound therapy is mechanical and thermal effects on tissue.

During operations, ultrasound is used as an “ultrasonic scalpel”, capable of cutting both soft and bone tissue.

The ability of ultrasound to crush bodies placed in liquid and create emulsions is used in the pharmaceutical industry in the manufacture of drugs. In the treatment of diseases such as tuberculosis, bronchial asthma, catarrh of the upper respiratory tract, aerosols of various medicinal substances obtained using ultrasound are used.

Currently, a new method has been developed for “welding” damaged or transplanted bone tissue using ultrasound. (ultrasonic osteosynthesis).

The destructive effect of ultrasound on microorganisms is used for sterilization.

The use of ultrasound for the blind is interesting. Thanks to ultrasonic location using the Orientir portable device, you can detect objects and determine their nature at a distance of up to 10 m.

The listed examples do not exhaust all medical and biological applications of ultrasound; the prospect of expanding these applications is truly enormous. Thus, we can expect, for example, the emergence of fundamentally new diagnostic methods with the introduction of ultrasound holography into medicine (see Chapter 24).

8.7. INFRASOUND

Infrasound is the name given to mechanical (elastic) waves with frequencies lower than those perceived by the human ear (20 Hz).

Sources of infrasound can be both natural objects (sea, earthquake, lightning discharges, etc.) and artificial ones (explosions, cars, machine tools, etc.).

Infrasound is often accompanied by audible noise, for example in a car, so difficulties arise in measuring and studying infrasound vibrations themselves.

Infrasound is characterized by weak absorption by various media, so it travels over a considerable distance. This makes it possible to detect an explosion at a great distance from the source by the propagation of infrasound in the earth’s crust, to predict a tsunami based on measured infrasound waves, etc. Since the wavelength of infrasound is longer than that of audible sounds, infrasound waves diffract better and penetrate into rooms, bypassing obstacles.

Infrasound has an adverse effect on the functional state of a number of body systems: fatigue, headache, drowsiness, irritation, etc. It is assumed that the primary mechanism of action of infrasound on the body is of a resonant nature. Resonance occurs at close values ​​of the frequency of the driving force and the frequency of natural oscillations (see 7.6). The frequency of natural vibrations of the human body in a lying position (3-4 Hz), standing (5-12 Hz), the frequency of natural vibrations of the chest (5-8 Hz), abdominal cavity (3-4 Hz), etc. correspond to the frequency of infrasounds.

Reducing the intensity level of infrasounds in residential, industrial and transport premises is one of the hygiene tasks.

8.8. VIBRATIONS

In technology, mechanical vibrations of various structures and machines are called vibrations

They also affect a person who comes into contact with vibrating objects. This effect can be both harmful and, under certain conditions, leading to vibration disease, as well as beneficial and therapeutic (vibration therapy and vibration massage).

The main physical characteristics of vibrations coincide with the characteristics of mechanical vibrations of bodies, these are:

Oscillation frequency or harmonic spectrum of anharmonic vibration;

Amplitude, velocity amplitude and acceleration amplitude;

Energy and average power of oscillations.

In addition, to understand the effect of vibrations on a biological object, it is important to imagine the propagation and attenuation of vibrations in the body. When studying this issue, models consisting of inertial masses, elastic and viscous elements are used (see 10.3).

Vibrations are the source of audible sounds, ultrasounds and infrasounds.

February 18, 2016

The world of home entertainment is quite varied and can include: watching movies on a good home theater system; exciting and exciting gameplay or listening to music. As a rule, everyone finds something of their own in this area, or combines everything at once. But whatever a person’s goals for organizing his leisure time and whatever extreme they go to, all these links are firmly connected by one simple and understandable word - “sound”. Indeed, in all of the above cases, we will be led by the hand by sound. But this question is not so simple and trivial, especially in cases where there is a desire to achieve high-quality sound in a room or any other conditions. To do this, it is not always necessary to buy expensive hi-fi or hi-end components (although it will be very useful), but a good knowledge of physical theory is sufficient, which can eliminate most of the problems that arise for anyone who sets out to obtain high-quality voice acting.

Next, the theory of sound and acoustics will be considered from the point of view of physics. In this case, I will try to make this as accessible as possible to the understanding of any person who, perhaps, is far from knowing physical laws or formulas, but nevertheless passionately dreams of realizing the dream of creating a perfect acoustic system. I do not presume to say that in order to achieve good results in this area at home (or in a car, for example), you need to know these theories thoroughly, but understanding the basics will allow you to avoid many stupid and absurd mistakes, and will also allow you to achieve the maximum sound effect from the system any level.

General theory of sound and musical terminology

What is it sound? This is the sensation that the auditory organ perceives "ear"(the phenomenon itself exists without the participation of the “ear” in the process, but this is easier to understand), which occurs when the eardrum is excited by a sound wave. The ear in this case acts as a “receiver” of sound waves of various frequencies.
Sound wave it is essentially a sequential series of compactions and discharges of the medium (most often the air medium under normal conditions) of various frequencies. The nature of sound waves is oscillatory, caused and produced by the vibration of any body. The emergence and propagation of a classical sound wave is possible in three elastic media: gaseous, liquid and solid. When a sound wave occurs in one of these types of space, some changes inevitably occur in the medium itself, for example, a change in air density or pressure, movement of air mass particles, etc.

Since a sound wave has an oscillatory nature, it has such a characteristic as frequency. Frequency measured in hertz (in honor of the German physicist Heinrich Rudolf Hertz), and denotes the number of oscillations over a period of time equal to one second. Those. for example, a frequency of 20 Hz indicates a cycle of 20 oscillations in one second. The subjective concept of its height also depends on the frequency of the sound. The more sound vibrations occur per second, the “higher” the sound appears. A sound wave also has another important characteristic, which has a name - wavelength. Wavelength It is customary to consider the distance that a sound of a certain frequency travels in a period equal to one second. For example, the wavelength of the lowest sound in the human audible range at 20 Hz is 16.5 meters, and the wavelength of the highest sound at 20,000 Hz is 1.7 centimeters.

The human ear is designed in such a way that it is capable of perceiving waves only in a limited range, approximately 20 Hz - 20,000 Hz (depending on the characteristics of a particular person, some are able to hear a little more, some less). Thus, this does not mean that sounds below or above these frequencies do not exist, they are simply not perceived by the human ear, going beyond the audible range. Sound above the audible range is called ultrasound, sound below the audible range is called infrasound. Some animals are able to perceive ultra and infra sounds, some even use this range for orientation in space (bats, dolphins). If sound passes through a medium that is not in direct contact with the human hearing organ, then such sound may not be heard or may be greatly weakened subsequently.

In the musical terminology of sound, there are such important designations as octave, tone and overtone of sound. Octave means an interval in which the frequency ratio between sounds is 1 to 2. An octave is usually very distinguishable by ear, while sounds within this interval can be very similar to each other. An octave can also be called a sound that vibrates twice as much as another sound in the same period of time. For example, the frequency of 800 Hz is nothing more than a higher octave of 400 Hz, and the frequency of 400 Hz in turn is the next octave of sound with a frequency of 200 Hz. The octave, in turn, consists of tones and overtones. Variable vibrations in a harmonic sound wave of the same frequency are perceived by the human ear as musical tone. High-frequency vibrations can be interpreted as high-pitched sounds, while low-frequency vibrations can be interpreted as low-pitched sounds. The human ear is capable of clearly distinguishing sounds with a difference of one tone (in the range of up to 4000 Hz). Despite this, music uses an extremely small number of tones. This is explained from considerations of the principle of harmonic consonance; everything is based on the principle of octaves.

Let's consider the theory of musical tones using the example of a string stretched in a certain way. Such a string, depending on the tension force, will be “tuned” to one specific frequency. When this string is exposed to something with one specific force, which causes it to vibrate, one specific tone of sound will be consistently observed, and we will hear the desired tuning frequency. This sound is called the fundamental tone. The frequency of the note “A” of the first octave is officially accepted as the fundamental tone in the musical field, equal to 440 Hz. However, most musical instruments never reproduce pure fundamental tones alone; they are inevitably accompanied by overtones called overtones. Here it is appropriate to recall an important definition of musical acoustics, the concept of sound timbre. Timbre- this is a feature of musical sounds that gives musical instruments and voices their unique, recognizable specificity of sound, even when comparing sounds of the same pitch and volume. The timbre of each musical instrument depends on the distribution of sound energy among overtones at the moment the sound appears.

Overtones form a specific coloring of the fundamental tone, by which we can easily identify and recognize a specific instrument, as well as clearly distinguish its sound from another instrument. There are two types of overtones: harmonic and non-harmonic. Harmonic overtones by definition are multiples of the fundamental frequency. On the contrary, if the overtones are not multiples and noticeably deviate from the values, then they are called non-harmonic. In music, operating with multiple overtones is practically excluded, so the term is reduced to the concept of “overtone,” meaning harmonic. For some instruments, such as the piano, the fundamental tone does not even have time to form; in a short period of time, the sound energy of the overtones increases, and then just as rapidly decreases. Many instruments create what is called a "transition tone" effect, where the energy of certain overtones is highest at a certain point in time, usually at the very beginning, but then changes abruptly and moves on to other overtones. The frequency range of each instrument can be considered separately and is usually limited to the fundamental frequencies that that particular instrument is capable of producing.

In sound theory there is also such a concept as NOISE. Noise- this is any sound that is created by a combination of sources that are inconsistent with each other. Everyone is familiar with the sound of tree leaves swaying by the wind, etc.

What determines the volume of sound? Obviously, such a phenomenon directly depends on the amount of energy transferred by the sound wave. To determine quantitative indicators of loudness, there is a concept - sound intensity. Sound intensity is defined as the flow of energy passing through some area of ​​space (for example, cm2) per unit of time (for example, per second). During normal conversation, the intensity is approximately 9 or 10 W/cm2. The human ear is capable of perceiving sounds over a fairly wide range of sensitivity, while the sensitivity of frequencies is heterogeneous within the sound spectrum. This way, the frequency range 1000 Hz - 4000 Hz, which most widely covers human speech, is best perceived.

Because sounds vary so greatly in intensity, it is more convenient to think of it as a logarithmic quantity and measure it in decibels (after the Scottish scientist Alexander Graham Bell). The lower threshold of hearing sensitivity of the human ear is 0 dB, the upper is 120 dB, also called the “pain threshold”. The upper limit of sensitivity is also perceived by the human ear not in the same way, but depends on the specific frequency. Low-frequency sounds must have much greater intensity than high-frequency sounds to trigger the pain threshold. For example, the pain threshold at a low frequency of 31.5 Hz occurs at a sound intensity level of 135 dB, when at a frequency of 2000 Hz the sensation of pain will appear at 112 dB. There is also the concept of sound pressure, which actually expands the usual explanation of the propagation of a sound wave in the air. Sound pressure- this is a variable excess pressure that arises in an elastic medium as a result of the passage of a sound wave through it.

Wave nature of sound

To better understand the system of sound wave generation, imagine a classic speaker located in a pipe filled with air. If the speaker makes a sharp movement forward, the air in the immediate vicinity of the diffuser is momentarily compressed. The air will then expand, thereby pushing the compressed air region along the pipe.
This wave movement will subsequently become sound when it reaches the auditory organ and “excites” the eardrum. When a sound wave occurs in a gas, excess pressure and excess density are created and particles move at a constant speed. About sound waves, it is important to remember the fact that the substance does not move along with the sound wave, but only a temporary disturbance of the air masses occurs.

If we imagine a piston suspended in free space on a spring and making repeated movements “back and forth”, then such oscillations will be called harmonic or sinusoidal (if we imagine the wave as a graph, then in this case we will get a pure sinusoid with repeated declines and rises). If we imagine a speaker in a pipe (as in the example described above) performing harmonic oscillations, then at the moment the speaker moves “forward” the well-known effect of air compression is obtained, and when the speaker moves “backwards” the opposite effect of rarefaction occurs. In this case, a wave of alternating compression and rarefaction will propagate through the pipe. The distance along the pipe between adjacent maxima or minima (phases) will be called wavelength. If the particles oscillate parallel to the direction of propagation of the wave, then the wave is called longitudinal. If they oscillate perpendicular to the direction of propagation, then the wave is called transverse. Typically, sound waves in gases and liquids are longitudinal, but in solids both types of waves can occur. Transverse waves in solids arise due to resistance to change in shape. The main difference between these two types of waves is that a transverse wave has the property of polarization (oscillations occur in a certain plane), while a longitudinal wave does not.

Sound speed

The speed of sound directly depends on the characteristics of the medium in which it propagates. It is determined (dependent) by two properties of the medium: elasticity and density of the material. The speed of sound in solids directly depends on the type of material and its properties. Velocity in gaseous media depends on only one type of deformation of the medium: compression-rarefaction. The change in pressure in a sound wave occurs without heat exchange with surrounding particles and is called adiabatic.
The speed of sound in a gas depends mainly on temperature - it increases with increasing temperature and decreases with decreasing temperature. Also, the speed of sound in a gaseous medium depends on the size and mass of the gas molecules themselves - the smaller the mass and size of the particles, the greater the “conductivity” of the wave and, accordingly, the greater the speed.

In liquid and solid media, the principle of propagation and the speed of sound are similar to how a wave propagates in air: by compression-discharge. But in these environments, in addition to the same dependence on temperature, the density of the medium and its composition/structure are quite important. The lower the density of the substance, the higher the speed of sound and vice versa. The dependence on the composition of the medium is more complex and is determined in each specific case, taking into account the location and interaction of molecules/atoms.

Speed ​​of sound in air at t, °C 20: 343 m/s
Speed ​​of sound in distilled water at t, °C 20: 1481 m/s
Speed ​​of sound in steel at t, °C 20: 5000 m/s

Standing waves and interference

When a speaker creates sound waves in a confined space, the effect of waves being reflected from the boundaries inevitably occurs. As a result, this most often occurs interference effect- when two or more sound waves overlap each other. Special cases of the phenomenon of interference are the formation of: 1) Beating waves or 2) Standing waves. Wave beats- this is the case when the addition of waves with similar frequencies and amplitudes occurs. The picture of the occurrence of beats: when two waves of similar frequencies overlap each other. At some point in time, with such an overlap, the amplitude peaks may coincide “in phase,” and the declines may also coincide in “antiphase.” This is how sound beats are characterized. It is important to remember that, unlike standing waves, phase coincidences of peaks do not occur constantly, but at certain time intervals. To the ear, this pattern of beats is distinguished quite clearly, and is heard as a periodic increase and decrease in volume, respectively. The mechanism by which this effect occurs is extremely simple: when the peaks coincide, the volume increases, and when the valleys coincide, the volume decreases.

Standing waves arise in the case of superposition of two waves of the same amplitude, phase and frequency, when when such waves “meet” one moves in the forward direction and the other in the opposite direction. In the area of ​​space (where the standing wave was formed), a picture of the superposition of two frequency amplitudes appears, with alternating maxima (the so-called antinodes) and minima (the so-called nodes). When this phenomenon occurs, the frequency, phase and attenuation coefficient of the wave at the place of reflection are extremely important. Unlike traveling waves, there is no energy transfer in a standing wave due to the fact that the forward and backward waves that form this wave transfer energy in equal quantities in both the forward and opposite directions. To clearly understand the occurrence of a standing wave, let’s imagine an example from home acoustics. Let's say we have floor-standing speaker systems in some limited space (room). Having them play something with a lot of bass, let's try to change the location of the listener in the room. Thus, a listener who finds himself in the zone of minimum (subtraction) of a standing wave will feel the effect that there is very little bass, and if the listener finds himself in a zone of maximum (addition) of frequencies, then the opposite effect of a significant increase in the bass region is obtained. In this case, the effect is observed in all octaves of the base frequency. For example, if the base frequency is 440 Hz, then the phenomenon of “addition” or “subtraction” will also be observed at frequencies of 880 Hz, 1760 Hz, 3520 Hz, etc.

Resonance phenomenon

Most solids have a natural resonance frequency. It is quite easy to understand this effect using the example of an ordinary pipe, open at only one end. Let's imagine a situation where a speaker is connected to the other end of the pipe, which can play one constant frequency, which can also be changed later. So, the pipe has its own resonance frequency, in simple terms - this is the frequency at which the pipe “resonates” or makes its own sound. If the frequency of the speaker (as a result of adjustment) coincides with the resonance frequency of the pipe, then the effect of increasing the volume several times will occur. This happens because the loudspeaker excites vibrations of the air column in the pipe with a significant amplitude until the same “resonant frequency” is found and the addition effect occurs. The resulting phenomenon can be described as follows: the pipe in this example “helps” the speaker by resonating at a specific frequency, their efforts add up and “result” in an audible loud effect. Using the example of musical instruments, this phenomenon can be easily seen, since the design of most instruments contains elements called resonators. It is not difficult to guess what serves the purpose of enhancing a certain frequency or musical tone. For example: a guitar body with a resonator in the form of a hole mating with the volume; The design of the flute tube (and all pipes in general); The cylindrical shape of the drum body, which itself is a resonator of a certain frequency.

Frequency spectrum of sound and frequency response

Since in practice there are practically no waves of the same frequency, it becomes necessary to decompose the entire sound spectrum of the audible range into overtones or harmonics. For these purposes, there are graphs that display the dependence of the relative energy of sound vibrations on frequency. This graph is called a sound frequency spectrum graph. Frequency spectrum of sound There are two types: discrete and continuous. A discrete spectrum plot displays individual frequencies separated by blank spaces. The continuous spectrum contains all sound frequencies at once.
In the case of music or acoustics, the usual graph is most often used Amplitude-Frequency Characteristics(abbreviated as "AFC"). This graph shows the dependence of the amplitude of sound vibrations on frequency throughout the entire frequency spectrum (20 Hz - 20 kHz). Looking at such a graph, it is easy to understand, for example, the strengths or weaknesses of a particular speaker or acoustic system as a whole, the strongest areas of energy output, frequency dips and rises, attenuation, and also to trace the steepness of the decline.

Propagation of sound waves, phase and antiphase

The process of propagation of sound waves occurs in all directions from the source. The simplest example to understand this phenomenon is a pebble thrown into water.
From the place where the stone fell, waves begin to spread across the surface of the water in all directions. However, let’s imagine a situation using a speaker in a certain volume, say a closed box, which is connected to an amplifier and plays some kind of musical signal. It is easy to notice (especially if you apply a powerful low-frequency signal, for example a bass drum) that the speaker makes a rapid movement “forward”, and then the same rapid movement “backward”. What remains to be understood is that when the speaker moves forward, it emits a sound wave that we hear later. But what happens when the speaker moves backward? And paradoxically, the same thing happens, the speaker makes the same sound, only in our example it propagates entirely within the volume of the box, without going beyond its limits (the box is closed). In general, in the above example one can observe quite a lot of interesting physical phenomena, the most significant of which is the concept of phase.

The sound wave that the speaker, being in the volume, emits in the direction of the listener is “in phase”. The reverse wave, which goes into the volume of the box, will be correspondingly antiphase. It remains only to understand what these concepts mean? Signal phase– this is the sound pressure level at the current moment in time at some point in space. The easiest way to understand the phase is by the example of the reproduction of musical material by a conventional floor-standing stereo pair of home speaker systems. Let's imagine that two such floor-standing speakers are installed in a certain room and play. In this case, both acoustic systems reproduce a synchronous signal of variable sound pressure, and the sound pressure of one speaker is added to the sound pressure of the other speaker. A similar effect occurs due to the synchronicity of signal reproduction from the left and right speakers, respectively, in other words, the peaks and troughs of the waves emitted by the left and right speakers coincide.

Now let’s imagine that the sound pressures still change in the same way (have not undergone changes), but only now they are opposite to each other. This can happen if you connect one speaker system out of two in reverse polarity ("+" cable from the amplifier to the "-" terminal of the speaker system, and "-" cable from the amplifier to the "+" terminal of the speaker system). In this case, the opposite signal will cause a pressure difference, which can be represented in numbers as follows: the left speaker will create a pressure of “1 Pa”, and the right speaker will create a pressure of “minus 1 Pa”. As a result, the total sound volume at the listener's location will be zero. This phenomenon is called antiphase. If we look at the example in more detail for understanding, it turns out that two speakers playing “in phase” create identical areas of air compaction and rarefaction, thereby actually helping each other. In the case of an idealized antiphase, the area of ​​compressed air space created by one speaker will be accompanied by an area of ​​rarefied air space created by the second speaker. This looks approximately like the phenomenon of mutual synchronous cancellation of waves. True, in practice the volume does not drop to zero, and we will hear a highly distorted and weakened sound.

The most accessible way to describe this phenomenon is as follows: two signals with the same oscillations (frequency), but shifted in time. In view of this, it is more convenient to imagine these displacement phenomena using the example of an ordinary round clock. Let's imagine that there are several identical round clocks hanging on the wall. When the second hands of this watch run synchronously, on one watch 30 seconds and on the other 30, then this is an example of a signal that is in phase. If the second hands move with a shift, but the speed is still the same, for example, on one watch it is 30 seconds, and on another it is 24 seconds, then this is a classic example of a phase shift. In the same way, phase is measured in degrees, within a virtual circle. In this case, when the signals are shifted relative to each other by 180 degrees (half a period), classical antiphase is obtained. Often in practice, minor phase shifts occur, which can also be determined in degrees and successfully eliminated.

Waves are plane and spherical. A plane wave front propagates in only one direction and is rarely encountered in practice. A spherical wavefront is a simple type of wave that originates from a single point and travels in all directions. Sound waves have the property diffraction, i.e. ability to go around obstacles and objects. The degree of bending depends on the ratio of the sound wavelength to the size of the obstacle or hole. Diffraction also occurs when there is some obstacle in the path of sound. In this case, two scenarios are possible: 1) If the size of the obstacle is much larger than the wavelength, then the sound is reflected or absorbed (depending on the degree of absorption of the material, the thickness of the obstacle, etc.), and an “acoustic shadow” zone is formed behind the obstacle. . 2) If the size of the obstacle is comparable to the wavelength or even less than it, then the sound diffracts to some extent in all directions. If a sound wave, while moving in one medium, hits the interface with another medium (for example, an air medium with a solid medium), then three scenarios can occur: 1) the wave will be reflected from the interface 2) the wave can pass into another medium without changing direction 3) a wave can pass into another medium with a change in direction at the boundary, this is called “wave refraction”.

The ratio of the excess pressure of a sound wave to the oscillatory volumetric velocity is called wave resistance. In simple words, wave impedance of the medium can be called the ability to absorb sound waves or “resist” them. The reflection and transmission coefficients directly depend on the ratio of the wave impedances of the two media. Wave resistance in a gaseous medium is much lower than in water or solids. Therefore, if a sound wave in air strikes a solid object or the surface of deep water, the sound is either reflected from the surface or absorbed to a large extent. This depends on the thickness of the surface (water or solid) on which the desired sound wave falls. When the thickness of a solid or liquid medium is low, sound waves almost completely “pass”, and vice versa, when the thickness of the medium is large, the waves are more often reflected. In the case of reflection of sound waves, this process occurs according to a well-known physical law: “The angle of incidence is equal to the angle of reflection.” In this case, when a wave from a medium with a lower density hits the boundary with a medium of higher density, the phenomenon occurs refraction. It consists in the bending (refraction) of a sound wave after “meeting” an obstacle, and is necessarily accompanied by a change in speed. Refraction also depends on the temperature of the medium in which reflection occurs.

In the process of propagation of sound waves in space, their intensity inevitably decreases; we can say that the waves attenuate and the sound weakens. In practice, encountering a similar effect is quite simple: for example, if two people stand in a field at some close distance (a meter or closer) and start saying something to each other. If you subsequently increase the distance between people (if they begin to move away from each other), the same level of conversational volume will become less and less audible. This example clearly demonstrates the phenomenon of a decrease in the intensity of sound waves. Why is this happening? The reason for this is various processes of heat exchange, molecular interaction and internal friction of sound waves. Most often in practice, sound energy is converted into thermal energy. Such processes inevitably arise in any of the 3 sound propagation media and can be characterized as absorption of sound waves.

The intensity and degree of absorption of sound waves depends on many factors, such as pressure and temperature of the medium. Absorption also depends on the specific sound frequency. When a sound wave propagates through liquids or gases, a friction effect occurs between different particles, which is called viscosity. As a result of this friction at the molecular level, the process of converting a wave from sound to heat occurs. In other words, the higher the thermal conductivity of the medium, the lower the degree of wave absorption. Sound absorption in gaseous media also depends on pressure (atmospheric pressure changes with increasing altitude relative to sea level). As for the dependence of the degree of absorption on the frequency of sound, taking into account the above-mentioned dependences of viscosity and thermal conductivity, the higher the frequency of sound, the higher the absorption of sound. For example, at normal temperature and pressure in air, the absorption of a wave with a frequency of 5000 Hz is 3 dB/km, and the absorption of a wave with a frequency of 50,000 Hz will be 300 dB/m.

In solid media, all the above dependencies (thermal conductivity and viscosity) are preserved, but several more conditions are added to this. They are associated with the molecular structure of solid materials, which can be different, with its own inhomogeneities. Depending on this internal solid molecular structure, the absorption of sound waves in this case can be different, and depends on the type of specific material. When sound passes through a solid body, the wave undergoes a number of transformations and distortions, which most often leads to the dispersion and absorption of sound energy. At the molecular level, a dislocation effect can occur when a sound wave causes a displacement of atomic planes, which then return to their original position. Or, the movement of dislocations leads to a collision with dislocations perpendicular to them or defects in the crystal structure, which causes their inhibition and, as a consequence, some absorption of the sound wave. However, the sound wave can also resonate with these defects, which will lead to distortion of the original wave. The energy of the sound wave at the moment of interaction with the elements of the molecular structure of the material is dissipated as a result of internal friction processes.

In this article I will try to analyze the features of human auditory perception and some of the subtleties and features of sound propagation.

Sound is a phenomenon that has excited human minds since ancient times. In fact, a world of various sounds arose on Earth long before human beings appeared on it. The first sounds were heard during the birth of our planet. They were caused by powerful impacts, vibrations of matter and the seething of hot matter.

Sound in the natural environment

When the first animals appeared on the planet, over time they developed an urgent need to receive as much information as possible about the surrounding reality. And since sound is one of the main carriers of information, representatives of the fauna began to undergo evolutionary changes in the brain, which gradually led to the formation of hearing organs.

Now primitive animals could receive, by capturing sound vibrations, the necessary information about danger, often emanating from objects invisible to the eye. Later, living beings learned to use sounds for other purposes. The scope of application of audio information grew in the process of the evolution of animals themselves. Sound signals began to serve as a means of primitive communication between them. With sounds they began to warn each other about danger, and it also served as a call to unity for creatures with herd instincts.

Man is the master of sounds

But only man managed to learn to fully use sound for his own purposes. At one point, people were faced with the need to transfer knowledge to each other and from generation to generation. Man subordinated to these goals the variety of sounds that he learned over time to produce and perceive. From this multitude of sounds speech subsequently emerged. Sound has also become a filler of leisure time. People discovered the euphony of the whistle of a bowstring being released, and the energy of the rhythmic striking of wooden objects against each other. This is how the first, simplest musical instruments arose, and therefore the art of music itself.

However, human communication and music are not the only sounds that appeared on Earth with the emergence of humans. Numerous labor processes were also accompanied by sounds: the production of various objects from stone and wood. And with the advent of civilization, with the invention of the wheel, people for the first time encountered the problem of loud noise. It is known that already in the ancient world, the sound of wheels on roads paved with stone often caused poor sleep among residents of roadside houses. To combat this noise, the first means of noise reduction was invented: straw was laid on the pavement.

Growing noise problem

When humanity learned the benefits of iron, the problem of noise began to acquire global proportions. By inventing gunpowder, man created a source of sound of such power that it was sufficient to cause noticeable damage to his own hearing aid. In the era of the industrial revolution, among such negative side effects as environmental pollution and depletion of natural resources, the problem of high-volume industrial noise occupies not the least place.

Anecdote from life

Nevertheless, even at present, not all manufacturers of industrial equipment pay at least some attention to this issue. The management of not all plants and factories is concerned about maintaining healthy hearing among their subordinates.

Sometimes you hear stories like this. The chief engineer of one of the large industrial enterprises ordered the installation of microphones in the noisiest workshops, connected to loudspeakers located outside the buildings. In his opinion, in this way the microphones will suck some of the noise out. Of course, as comical as this story is, it makes you think about the reasons for such illiteracy in matters relating to noise reduction and sound insulation. And there is only one reason for this - in educational institutions of higher, secondary vocational and secondary specialized levels of education, only in recent decades have they begun to introduce special courses in acoustics.

The Science of Sound

The first attempts to understand the nature of sound were made by Pythagoras, who studied the vibrations of a string. After Pythagoras, for many centuries this area did not arouse any interest among researchers. Of course, a number of ancient scientists were engaged in constructing their own acoustic theories, but these scientific researches were not based on mathematical calculations, but were more like disparate philosophical reasoning.

And only after more than a thousand years did Galileo lay the foundation for a new science of sound - acoustics. The most prominent pioneers in this area were Rayleigh and Helmholtz. They created the theoretical basis of modern acoustics in the nineteenth century. Hermann Helmholtz is mainly famous for his studies of the properties of resonators, and Rayleigh became a Nobel laureate for his fundamental work on the theory of sound.

Main directions of modern acoustics

Numerous scientific works on the study of the nature of noise and the issues of noise reduction and sound insulation were published some time later. The first work in this area concerned mainly the noise produced by aircraft and ground transport. But over time, the boundaries of these studies have expanded significantly. At the moment, most industrialized countries have their own research institutes that are engaged in developing solutions to these problems.

Today, the following sections of acoustics are best known: general, geometric, architectural, construction, psychological, musical, biological, electrical, aviation, transport, medical, ultrasound, quantum, speech, digital. The following chapters will examine some of these areas of sound science.

General provisions

First of all, we should define the science discussed in this article. Acoustics is the field of knowledge about the nature of sound. This science studies phenomena such as the occurrence, propagation, sensation of sound and the various effects produced by sound on the organs of hearing. Like all other sciences, acoustics has its own conceptual apparatus.

Acoustics is a science considered to be one of the branches of physical science. At the same time, it is also an interdisciplinary field, that is, it has close connections with other areas of knowledge. The interaction of acoustics with mechanics, architecture, music theory, psychology, electronics, and mathematics is most clearly visible. The most important formulas of acoustics concern the propagation properties of sound waves in an elastic medium: equations of plane and standing waves, formulas for calculating wave speed.

Application in music

Musical acoustics is a branch that studies musical sounds from a physics perspective. This industry is also interdisciplinary. Scientific works on musical acoustics actively use the achievements of mathematical science, music theory and psychology. The basic concepts of this science: pitch, dynamic and timbral shades of sounds used in music. This section of acoustics is primarily aimed at studying the sensations that arise when humans perceive sounds, as well as the characteristics of musical intonation (reproduction of sounds of a certain pitch). One of the most extensive research topics in musical acoustics is the topic of musical instruments.

Application in practice

Music theorists have applied research on musical acoustics to construct concepts of music based on the natural sciences. Physicists and psychologists have studied issues of musical perception. Domestic scientists who worked in this field worked both on the development of a theoretical basis (N. Garbuzov is known for his theory of zones of musical perception) and on the application of achievements in practice (L. Termen, A. Volodin, E. Murzin were engaged in the design of electric musical instruments ).

In recent years, interdisciplinary scientific works have increasingly begun to appear, in which the peculiarities of the acoustics of buildings belonging to different architectural styles and eras are comprehensively examined. Data obtained from research in this area are used to develop methods for developing musical ear and tuning techniques for musical instruments. Therefore, we can conclude that musical acoustics is a branch of science that has not lost its relevance today.

Ultrasound

Not all sounds can be perceived by human hearing. Ultrasonic acoustics is a branch of acoustics that studies sound vibrations with a range of twenty kHz. Sounds of this frequency are beyond human perception. Ultrasound is divided into three types: low-frequency, mid-frequency, high-frequency. Each type has its own specific reproduction and practical application. Ultrasounds can be created not only artificially. They are often found in wildlife. Thus, the noise produced by the wind consists partly of ultrasound. Also, such sounds are reproduced by some animals and are captured by their hearing organs. Everyone knows that the bat is one of these creatures.

Ultrasonic acoustics is a branch of acoustics that has found practical application in medicine, in various scientific experiments and research, and in the military industry. In particular, at the beginning of the twentieth century in Russia a device was invented for detecting underwater icebergs. The operation of this device was based on the generation and capture of ultrasonic waves. From this example it is clear that ultrasonic acoustics is a science whose achievements have been used in practice for more than a hundred years.

Accent placement: ACOUSTICS

ACOUSTICS (Greek akustikos - auditory) - the study of sound; a branch of physics that studies the properties, occurrence, propagation and reception of elastic waves in gaseous, liquid or solid media.

A. - one of the most ancient areas of physics - arose in connection with the need to explain the phenomena of hearing and speech. Thus, even Empedocles (490-430 BC) explained the propagation and perception of sounds by the movements of a special (subtle) substance emanating from the sounding body and entering the ear. Aristotle (384-322 BC) already understood that a sounding body causes compression and rarefaction of air, and was able to explain the process of the occurrence of echo. He clearly distinguished between the height, strength and timbre of sound and associated them with differences in the speed and amount of moving air and with the structure of the vocal apparatus. Pythagoras (6th century BC) was the first to formulate the laws of string vibration.

A milestone in the development of acoustics was the work of Galileo and Mersenne (17th century), who established the quantitative laws of vibration of strings and were the first to determine the speed of sound in air. Gassendi (17th century) established that the speed of sound does not depend on its height. The brothers Weber (1825) and Savard (1820) showed that the propagation of sound in liquids and elastic bodies follows the same laws as in air. In 1863, Helmholtz’s book “The Doctrine of Sound Sensations” was published, and in 1877-1878. - Rayleigh's work "Theory of Sound".

Helmholtz explained the physical nature of sounds, based on the method he developed for analyzing sounds (Helmholtz resonators), and explained the perception of sound by the laws of physics.

A new stage in the development of acoustics began in connection with the development of electronic technology, the creation of electronic amplifiers, and the discovery of new ways to generate sounds up to very high frequencies (millions of vibrations per second). A. began to develop especially intensively in connection with the problem of radio and television broadcasting.

Modern architecture can be divided into general, or theoretical, physiological, medical, musical, architectural, technical, and atmospheric; Electroacoustics and hydroacoustics are also distinguished.

General, ortheoretical, acoustics studies (theoretically and experimentally) the processes of emergence and spread sound(see), as well as methods of acoustic measurements.

An oscillating body (source of oscillations) creates in the environment zones of alternating increase and decrease in pressure, propagating in different directions in the form of elastic oscillations (waves) with speeds determined by the properties of the medium in which they propagate. For example, the speed of propagation of elastic waves in air at t° 0° is 331 m/sec, in water - 1440-1500 m/sec, in bone tissue - 3380 m/sec. Elastic vibrations are characterized by vibration frequency (f), wavelength (λ), and vibration intensity (I). The oscillation frequency is determined in hertz ( Hz); 1 Hz equal to one vibration per second. If the frequency of elastic vibrations is in the range of 16-20000 Hz, then they are perceived by the human hearing organ in the form of sound, the height of which is determined by the frequency of vibrations; in this case, higher frequencies correspond to higher sounds.

The strength of sound is determined by the intensity of the sound or the amount of sound energy flowing through 1 cm 2 in 1 sec. The intensity of vibration is maximum at the source of vibration and decreases with distance.

Fluctuations below 16 and above 20000 Hz(with deviations in one direction or another) are not perceived by the human ear in the form of sounds and are called infrasound(mass media ultrasounds(cm.). At the same time, a person through the bones of the skull is able to perceive ultrasound with a frequency of about 100,000-150,000 Hz. Infrasonic vibrations can be perceived by the body vibrotactilely (see. Vibration). The limits of perception of sound waves by animals differ significantly from the indicated figures (for example, guinea pigs, hamsters and certain other animals perceive sounds with a frequency of up to 100,000 Hz).

Physiological acoustics studies the physics and biophysics of the organs of hearing and speech, as well as the consequences of the action of elastic vibrations, since the latter are capable of exerting mechanical, thermal and physical-chemical effects on biological objects (including the body as a whole). impact. The intensity of sound energy and frequency are important. So, for example, at a sound intensity of the order of 10 -4 W/cm 2 a painful sensation occurs. Intense sounds, even below the threshold of pain, have a harmful effect on health and performance. Prolonged exposure to loud noise may cause hearing loss(see), sometimes to deafness(see) or specific damage to the organ of hearing as a result of exposure to sounds of excessive force (see. Acoustic trauma). At the same time, the sensitivity of the human ear to sounds of different pitches is not the same. The ear is most sensitive to tones 1000-3000 Hz.

Elastic vibrations of different frequency ranges cause specific effects, but all frequency ranges have something in common in the nature of their action: 1) at low intensities, the sound effect on the biological substrate is practically absent; 2) at medium intensities, the impact of elastic vibrations causes mechanical, thermal and physical-chemical. changes; 3) at high intensities, irreversible changes occur in the biological substrate, sometimes leading to the death of the organism (see. Sound, biological effect of high-intensity sounds).

Medical acoustics, using the techniques and methods of physiological vibration, explores and seeks the possibilities of using elastic vibrations in practical medicine (diagnosis, therapy, surgery).

Particular attention is paid to the study of elastic vibrations that occur in the human body during the operation of its internal organs and circulatory system (for example, the mechanical activity of the heart, lungs, pulse waves, etc.). These studies, carried out under normal and pathological conditions, serve as the basis for the creation of acoustic instruments and devices, as well as certain research methods (for example, auscultation, pneumography, phonocardiography). To diagnose diseases of the hearing organ, as well as to examine the auditory analyzer, an external sound generator is used (see. Audiometry, audiometer).

One of the areas of use of sound vibrations in medicine is devices for prosthetics of the vocal apparatus and correction of the patient’s hearing (see. Hearing Aids).

Ultrasound is especially widely used. It is used for therapy, providing high therapeutic efficiency, and is increasingly used for diagnostic purposes, complementing radiography. Ultrasound has found application in surgery, due to the ease of obtaining powerful ultrasounds, if necessary in the form of thin beams with the ability to focus them like optical beams. This is used in the treatment of certain brain diseases, when it is necessary to locally necrotize tissue (the intensity of each of the ultrasound rays directed at a given point is insufficient to cause any pathological change, but at the focal point their total intensity is sufficient to necrotize the tissue).

Ultrasounds have pronounced bactericidal properties, which have found application, for example, in the sterilization of milk, canned food, etc. Ultrasound is also used in cleaning instruments (based on the phenomenon of cavitation), in particular surgical ones, and primarily hollow needles for injections (more For details on the use of ultrasound in medicine, see Ultrasound).

One of the aspects of the practical application of research results in the field of A. is dignity. rationing noise(cm.). The noise level and its spectral analysis are measured using sound level meters and sound spectrum analyzers. Based on special work that takes into account the harmful effects of noise on the human body, maximum permissible noise standards have been developed for various conditions. Similar work has been carried out in the field of sanitary regulation. vibrations(cm.).

See above for the main uses of acoustics in medical practice.

Architectural acoustics studies sound processes in enclosed spaces from the point of view of ensuring good audibility of speech and music at all points where listeners may be, etc.

Atmospheric acoustics deals with Ch. arr. studying the patterns of sound propagation in a free atmosphere.

Technical acoustics considers mainly the practical possibility of applying A. to the technology of transmitting individual sounds, speech and music, which is related to Ch. arr. with problems converting sound energy into electrical energy; Therefore, technical engineering is often called electroacoustics. Technical analysis, along with general or theoretical analysis, deals with the creation of measuring, receiving, and transmitting equipment.

A special section of technical engineering is hydroacoustics, which studies the propagation of sound waves and rays in a liquid medium, and primarily in water.

Bibliography.: Beranek L. Acoustic measurements, trans. from English, M., 1952; Krasilnikov V. A. Sound and ultrasonic waves in air, water and solids, M., 1960; Lamb G. Dynamic theory of sound, trans. from English, M., 1960; Paul R. V. Mechanics, acoustics and the doctrine of heat, trans. from German, M., 1971; Strett D. W. (Rayleigh D. V.), Theory of Sound, trans. from English, vol. 1 - 2, M., 1955; Skuchik E. Fundamentals of Acoustics, trans. from German, vol. 1 - 2, M., 19 58 - 1959; Morse P. M. a. Ingard K. U. Theoretical acoustics, N.Y. a. o., 1968.

L. A. Vodolazsky, A. A. Chevnenko.

Sources:

1. Big medical encyclopedia. Volume 1/Editor-in-Chief Academician B.V. Petrovsky; publishing house "Soviet Encyclopedia"; Moscow, 1974.- 576 p.

I. Subject of physics. Her tasks. Sound and its characteristics.

Physics - the science of the properties and forms of existence of matter.

Biophysics - medical and biological science that studies physical processes and phenomena in living systems, including under various external influences.

Goals andtasksmedical and biological physics course:

Get acquainted with the physical and biophysical mechanisms occurring in the tissues, organs and systems of the body.

Study the physical and biophysical characteristics of organs and tissues and the physical principles of their operation.

To become familiar with the physical basis of diagnostic and treatment methods.

Get acquainted with the physical basis of the operating methods of medical equipment.

Study the influence of external factors on the body.

Features of modern physics.

a) Modern physics has border areas with other sciences.

b) Physics is divided into a number of narrow areas according to different criteria:

by scope of research;

by subjects of research.

The role of physics for other sciences is increasing; it gives them theories, principles, systems of units, experimental results, creates the basis for the design of medical equipment, and explains various physical and biological processes.

Features of biophysics:

It is a frontier science.

Has narrow areas:

general and private;

theoretical, experimental and applied;

studies the biophysics of plants, animals and humans;

quantum biophysics;

molecular, cellular, biophysics of tissues, organs, systems, populations.

Sound, its characteristics.

Acoustics is the science of the receipt, propagation and properties of mechanical waves and the interaction of these waves with physical and biophysical objects.

Types of acoustics:

Technical- studies the reception and distribution of sound, develops sound research methods.

Architectural- explores issues of obtaining good audibility or protecting premises (for example, from noise).

Biological- explores the production and use of sound by living organisms.

Medical- explores the physics and biophysics of hearing and speech, the possibilities of using sound for diagnosis and treatment. A distinction must be made between the use of audible sound and ultrasound.

Main tasks of medical acoustics :

development of hygienic standards for the use of sound in science and industry;

development of sound diagnostic and treatment methods;

development of ultrasound diagnostic and treatment methods.

Sound as a physical phenomenon.

Sound- a type of mechanical vibrations propagated in elastic media mainly in the form of longitudinal waves. Sound does not travel in a vacuum.

Sound wave- mechanical disturbance propagated in an elastic medium.

Sound vibrations- mechanical vibrations of conventional particles of the medium.

Conditional particles- volumes of the medium that are quite small compared to the wavelength.

Sound field- part of the space in which a sound wave propagates.

Classification of sound waves:

1. By frequency

infrasound (v< 16Гц)

audible sound (16Hz< v < 20000Гц)

ultrasound (20000Hz< v <100МГц)

hypersound (v > 100 MHz)

(all boundaries are conditional)

Infrasound, ultrasound and hypersound are not perceived by the auditory analyzer.

In the direction of displacement of medium particles:

Longitudinal - waves in which vibrations of the particles of the medium occur along the direction of propagation of the wave.

Transverse - waves in which vibrations of particles of the medium occur in a direction perpendicular to the direction of propagation of the wave.

In liquids and gases, elastic forces arise only when volume changes; only longitudinal waves are formed in them.

In solids, elastic forces arise both when volume changes and when shape changes; both longitudinal and transverse waves are formed in them, and the speed of longitudinal waves is approximately half the speed of transverse waves.

3. According to vibration shape:

Harmonic spectrum