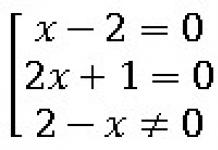How to remember formulas for reducing trigonometric functions? It's easy if you use an association. This association was not invented by me. As already mentioned, a good association should “catch”, that is, evoke vivid emotions. I cannot call the emotions caused by this association positive. But it gives a result - it allows you to remember reduction formulas, which means it has the right to exist. After all, if you don't like it, you don't have to use it, right?
The reduction formulas have the form: sin(πn/2±α), cos(πn/2±α), tg(πn/2±α), ctg(πn/2±α). Remember that +α gives counterclockwise movement, - α gives clockwise movement.
To work with reduction formulas, you need two points:
1) put the sign that the initial function has (in textbooks they write: reducible. But in order not to get confused, it is better to call it initial), if we consider α to be the angle of the first quarter, that is, small.
2) Horizontal diameter - π±α, 2π±α, 3π±α... - in general, when there is no fraction, the name of the function does not change. Vertical π/2±α, 3π/2±α, 5π/2±α... - when there is a fraction, the name of the function changes: sine - to cosine, cosine - to sine, tangent - to cotangent and cotangent - to tangent. 
Now, actually, the association:
vertical diameter (there is a fraction) -
standing drunk. What will happen to him early?
or is it too late? That's right, it will fall.
The function name will change.
If the diameter is horizontal, the drunk is already lying down. He's probably sleeping. Nothing will happen to him; he has already assumed a horizontal position. Accordingly, the name of the function does not change.
That is, sin(π/2±α), sin(3π/2±α), sin(5π/2±α), etc. give ±cosα,
and sin(π±α), sin(2π±α), sin(3π±α), … - ±sinα.
We already know how.
How it works? Let's look at examples.
1) cos(π/2+α)=?
We become π/2. Since +α means we go forward, counterclockwise. We find ourselves in the second quarter, where the cosine has a “-“ sign. The name of the function changes (“a drunk person is standing”, which means he will fall). So,
cos(π/2+α)=-sin α.
Let's get to 2π. Since -α - we go backwards, that is, clockwise. We find ourselves in the IV quarter, where the tangent has a “-“ sign. The name of the function does not change (the diameter is horizontal, “the drunk is already lying down”). Thus, tan(2π-α)=- tanα.
3) ctg²(3π/2-α)=?
Examples in which a function is raised to an even power are even simpler to solve. The even degree “-” removes it, that is, you just need to find out whether the name of the function changes or remains. The diameter is vertical (there is a fraction, “standing drunk”, it will fall), the name of the function changes. We get: ctg²(3π/2-α)= tan²α.
And another problem B11 on the same topic - from the real Unified State Examination in mathematics.
Task. Find the meaning of the expression:
In this short video tutorial we will learn how to apply reduction formulas for solving real problems B11 from the Unified State Examination in mathematics. As you can see, we have two trigonometric expressions, each containing sines and cosines, as well as some pretty brutal numerical arguments.
Before solving these problems, let's remember what reduction formulas are. So, if we have expressions like:
Then we can get rid of the first term (of the form k · π/2) according to special rules. Let's draw a trigonometric circle and mark the main points on it: 0, π/2; π; 3π/2 and 2π. Then we look at the first term under the sign of the trigonometric function. We have:
- If the term we are interested in lies on the vertical axis of the trigonometric circle (for example: 3π/2; π/2, etc.), then the original function is replaced by a co-function: sine is replaced by cosine, and cosine, on the contrary, by sine.
- If our term lies on the horizontal axis, then the original function does not change. We simply remove the first term in the expression and that’s it.
Thus, we obtain a trigonometric function that does not contain terms of the form k · π/2. However, the work with reduction formulas does not end there. The fact is that our new function, obtained after “discarding” the first term, may have a plus or minus sign in front of it. How to identify this sign? Now we'll find out.
Let's imagine that the angle α remaining inside the trigonometric function after transformations has a very small degree measure. But what does “small measure” mean? Let's say α ∈ (0; 30°) - this is quite enough. Let's take an example of the function:
Then, following our assumptions that α ∈ (0; 30°), we conclude that the angle 3π/2 − α lies in the third coordinate quarter, i.e. 3π/2 − α ∈ (π; 3π/2). Let us remember the sign of the original function, i.e. y = sin x on this interval. Obviously, the sine in the third coordinate quarter is negative, since by definition, the sine is the ordinate of the end of the moving radius (in short, the sine is the y coordinate). Well, the y coordinate in the lower half-plane always takes negative values. This means that in the third quarter y is also negative.
Based on these reflections, we can write down the final expression:
Problem B11 - Option 1
These same techniques are quite suitable for solving problem B11 from the Unified State Examination in mathematics. The only difference is that in many real B11 problems, instead of a radian measure (i.e. numbers π, π/2, 2π, etc.) a degree measure is used (i.e. 90°, 180°, 270° and etc.). Let's look at the first task:
Let's look at the numerator first. cos 41° is a non-tabular value, so we can't do anything with it. Let's leave it like that for now.
Now let's look at the denominator:
sin 131° = sin (90° + 41°) = cos 41°
Obviously, this is a reduction formula, so the sine is replaced by a cosine. In addition, the angle 41° lies on the segment (0°; 90°), i.e. in the first coordinate quadrant - exactly as required to apply the reduction formulas. But then 90° + 41° is the second coordinate quarter. The original function y = sin x is positive there, so we put a plus sign in front of the cosine at the last step (in other words, we didn’t put anything).
It remains to deal with the last element:
cos 240° = cos (180° + 60°) = −cos 60° = −0.5
Here we see that 180° is the horizontal axis. Consequently, the function itself will not change: there was a cosine - and the cosine will also remain. But the question arises again: will plus or minus appear before the resulting expression cos 60°? Note that 180° is the third coordinate quarter. The cosine there is negative, therefore, the cosine will eventually have a minus sign in front of it. In total, we get the construction −cos 60° = −0.5 - this is a tabular value, so everything is easy to calculate.
Now we substitute the resulting numbers into the original formula and get:
As you can see, the number cos 41° in the numerator and denominator of the fraction is easily reduced, and the usual expression remains, which is equal to −10. In this case, the minus can either be taken out and placed in front of the fraction sign, or “kept” next to the second factor until the very last step of the calculations. In any case, the answer will be −10. That's it, problem B11 is solved!
Problem B14 - option 2
Let's move on to the second task. We have a fraction before us again:
Well, 27° lies in the first coordinate quarter, so we won’t change anything here. But sin 117° needs to be written (without any square for now):
sin 117° = sin (90° + 27°) = cos 27°
Obviously, before us again reduction formula: 90° is the vertical axis, therefore the sine will change to cosine. In addition, the angle α = 117° = 90° + 27° lies in the second coordinate quadrant. The original function y = sin x is positive there, therefore, after all the transformations, there is still a plus sign in front of the cosine. In other words, nothing is added there - we leave it like that: cos 27°.
We return to the original expression that needs to be calculated:
As we see, after the transformations, the main trigonometric identity arose in the denominator: sin 2 27° + cos 2 27° = 1. Total −4: 1 = −4 - so we found the answer to the second problem B11.
As you can see, with the help of reduction formulas such problems from the Unified State Examination in mathematics are solved literally in a couple of lines. No sine of the sum and cosine of the difference. All we need to remember is just the trigonometric circle.
This article is devoted to a detailed study of trigonometric reduction formulas. A complete list of reduction formulas is given, examples of their use are shown, and proof of the correctness of the formulas is given. The article also provides a mnemonic rule that allows you to derive reduction formulas without memorizing each formula.
Yandex.RTB R-A-339285-1
Reduction formulas. List
Reduction formulas allow you to reduce basic trigonometric functions of angles of arbitrary magnitude to functions of angles lying in the range from 0 to 90 degrees (from 0 to π 2 radians). Operating with angles from 0 to 90 degrees is much more convenient than working with arbitrarily large values, which is why reduction formulas are widely used in solving trigonometry problems.
Before we write down the formulas themselves, let us clarify several important points for understanding.
- The arguments of trigonometric functions in reduction formulas are angles of the form ± α + 2 π · z, π 2 ± α + 2 π · z, 3 π 2 ± α + 2 π · z. Here z is any integer, and α is an arbitrary rotation angle.
- It is not necessary to learn all the reduction formulas, the number of which is quite impressive. There is a mnemonic rule that makes it easy to derive the desired formula. We will talk about the mnemonic rule later.
Now let's move directly to the reduction formulas.
Reduction formulas allow you to move from working with arbitrary and arbitrarily large angles to working with angles ranging from 0 to 90 degrees. Let's write all the formulas in table form.
Reduction formulas
sin α + 2 π z = sin α , cos α + 2 π z = cos α t g α + 2 π z = t g α , c t g α + 2 π z = c t g α sin - α + 2 π z = - sin α , cos - α + 2 π z = cos α t g - α + 2 π z = - t g α , c t g - α + 2 π z = - c t g α sin π 2 + α + 2 π z = cos α , cos π 2 + α + 2 π z = - sin α t g π 2 + α + 2 π z = - c t g α , c t g π 2 + α + 2 π z = - t g α sin π 2 - α + 2 π z = cos α , cos π 2 - α + 2 π z = sin α t g π 2 - α + 2 π z = c t g α , c t g π 2 - α + 2 π z = t g α sin π + α + 2 π z = - sin α , cos π + α + 2 π z = - cos α t g π + α + 2 π z = t g α , c t g π + α + 2 π z = c t g α sin π - α + 2 π z = sin α , cos π - α + 2 π z = - cos α t g π - α + 2 π z = - t g α , c t g π - α + 2 π z = - c t g α sin 3 π 2 + α + 2 π z = - cos α , cos 3 π 2 + α + 2 π z = sin α t g 3 π 2 + α + 2 π z = - c t g α , c t g 3 π 2 + α + 2 π z = - t g α sin 3 π 2 - α + 2 π z = - cos α , cos 3 π 2 - α + 2 π z = - sin α t g 3 π 2 - α + 2 π z = c t g α , c t g 3 π 2 - α + 2 π z = t g α
In this case, the formulas are written in radians. However, you can also write them using degrees. It is enough just to convert radians to degrees, replacing π by 180 degrees.
Examples of using reduction formulas
We will show how to use reduction formulas and how these formulas are used to solve practical examples.
The angle under the sign of the trigonometric function can be represented not in one, but in many ways. For example, the argument of a trigonometric function can be represented in the form ± α + 2 π z, π 2 ± α + 2 π z, π ± α + 2 π z, 3 π 2 ± α + 2 π z. Let's demonstrate this.
Let's take the angle α = 16 π 3. This angle can be written like this:
α = 16 π 3 = π + π 3 + 2 π 2 α = 16 π 3 = - 2 π 3 + 2 π 3 α = 16 π 3 = 3 π 2 - π 6 + 2 π
Depending on the representation of the angle, the appropriate reduction formula is used.
Let's take the same angle α = 16 π 3 and calculate its tangent
Example 1: Using reduction formulas
α = 16 π 3 , t g α = ?
Let us represent the angle α = 16 π 3 as α = π + π 3 + 2 π 2
This representation of the angle will correspond to the reduction formula
t g (π + α + 2 π z) = t g α
t g 16 π 3 = t g π + π 3 + 2 π 2 = t g π 3
Using the table, we indicate the value of the tangent
Now we use another representation of the angle α = 16 π 3.
Example 2: Using reduction formulas
α = 16 π 3 , t g α = ? α = - 2 π 3 + 2 π 3 t g 16 π 3 = t g - 2 π 3 + 2 π 3 = - t g 2 π 3 = - (- 3) = 3
Finally, for the third representation of the angle we write
Example 3. Using reduction formulas
α = 16 π 3 = 3 π 2 - π 6 + 2 π t g 3 π 2 - α + 2 π z = c t g α t g α = t g (3 π 2 - π 6 + 2 π) = c t g π 6 = 3
Now let's give an example of using more complex reduction formulas
Example 4: Using reduction formulas
Let's imagine sin 197° through the sine and cosine of an acute angle.
In order to be able to apply reduction formulas, you need to represent the angle α = 197 ° in one of the forms
± α + 360 ° z, 90 ° ± α + 360 ° z, 180 ° ± α + 360 ° z, 270 ° ± α + 360 ° z. According to the conditions of the problem, the angle must be acute. Accordingly, we have two ways to represent it:
197° = 180° + 17° 197° = 270° - 73°
We get
sin 197° = sin (180° + 17°) sin 197° = sin (270° - 73°)
Now let's look at the reduction formulas for sines and choose the appropriate ones
sin (π + α + 2 πz) = - sinα sin (3 π 2 - α + 2 πz) = - cosα sin 197 ° = sin (180 ° + 17 ° + 360 ° z) = - sin 17 ° sin 197 ° = sin (270 ° - 73 ° + 360 ° z) = - cos 73 °
Mnemonic rule
There are many reduction formulas, and, fortunately, there is no need to memorize them. There are regularities by which reduction formulas can be derived for different angles and trigonometric functions. These patterns are called mnemonic rules. Mnemonics is the art of memorization. The mnemonic rule consists of three parts, or contains three stages.
Mnemonic rule
1. The argument of the original function is represented in one of the following forms:
± α + 2 πz π 2 ± α + 2 πz π ± α + 2 πz 3 π 2 ± α + 2 πz
Angle α must lie between 0 and 90 degrees.
2. The sign of the original trigonometric function is determined. The function written on the right side of the formula will have the same sign.
3. For angles ± α + 2 πz and π ± α + 2 πz the name of the original function remains unchanged, and for angles π 2 ± α + 2 πz and 3 π 2 ± α + 2 πz, respectively, it changes to “cofunction”. Sine - cosine. Tangent - cotangent.
To use the mnemonic guide for reduction formulas, you need to be able to determine the signs of trigonometric functions based on the quarters of the unit circle. Let's look at examples of using the mnemonic rule.
Example 1: Using a mnemonic rule
Let us write down the reduction formulas for cos π 2 - α + 2 πz and t g π - α + 2 πz. α is the log of the first quarter.
1. Since by condition α is the log of the first quarter, we skip the first point of the rule.
2. Determine the signs of the functions cos π 2 - α + 2 πz and t g π - α + 2 πz. The angle π 2 - α + 2 πz is also the angle of the first quarter, and the angle π - α + 2 πz is in the second quarter. In the first quarter, the cosine function is positive, and the tangent in the second quarter has a minus sign. Let's write down what the required formulas will look like at this stage.
cos π 2 - α + 2 πz = + t g π - α + 2 πz = -
3. According to the third point, for the angle π 2 - α + 2 π the name of the function changes to Confucius, and for the angle π - α + 2 πz remains the same. Let's write down:
cos π 2 - α + 2 πz = + sin α t g π - α + 2 πz = - t g α
Now let’s look at the formulas given above and make sure that the mnemonic rule works.
Let's look at an example with a specific angle α = 777°. Let us reduce sine alpha to the trigonometric function of an acute angle.
Example 2: Using a mnemonic rule
1. Imagine the angle α = 777 ° in the required form
777° = 57° + 360° 2 777° = 90° - 33° + 360° 2
2. The original angle is the angle of the first quarter. This means that the sine of the angle has a positive sign. As a result we have:
3. sin 777° = sin (57° + 360° 2) = sin 57° sin 777° = sin (90° - 33° + 360° 2) = cos 33°
Now let's look at an example that shows how important it is to correctly determine the sign of the trigonometric function and correctly represent the angle when using the mnemonic rule. Let's repeat it again.
Important!
Angle α must be acute!
Let's calculate the tangent of the angle 5 π 3. From the table of values of the main trigonometric functions, you can immediately take the value t g 5 π 3 = - 3, but we will apply the mnemonic rule.
Example 3: Using a mnemonic rule
Let's imagine the angle α = 5 π 3 in the required form and use the rule
t g 5 π 3 = t g 3 π 2 + π 6 = - c t g π 6 = - 3 t g 5 π 3 = t g 2 π - π 3 = - t g π 3 = - 3
If we represent the alpha angle in the form 5 π 3 = π + 2 π 3, then the result of applying the mnemonic rule will be incorrect.
t g 5 π 3 = t g π + 2 π 3 = - t g 2 π 3 = - (- 3) = 3
The incorrect result is due to the fact that the angle 2 π 3 is not acute.
The proof of the reduction formulas is based on the properties of periodicity and symmetry of trigonometric functions, as well as on the property of shift by angles π 2 and 3 π 2. The proof of the validity of all reduction formulas can be carried out without taking into account the term 2 πz, since it denotes a change in the angle by an integer number of full revolutions and precisely reflects the property of periodicity.
The first 16 formulas follow directly from the properties of the basic trigonometric functions: sine, cosine, tangent and cotangent.
Here is a proof of the reduction formulas for sines and cosines
sin π 2 + α = cos α and cos π 2 + α = - sin α
Let's look at a unit circle, the starting point of which, after a rotation through an angle α, goes to the point A 1 x, y, and after a rotation through an angle π 2 + α - to a point A 2. From both points we draw perpendiculars to the abscissa axis.
Two right triangles O A 1 H 1 and O A 2 H 2 are equal in hypotenuse and adjacent angles. From the location of points on the circle and the equality of triangles, we can conclude that point A 2 has coordinates A 2 - y, x. Using the definitions of sine and cosine, we write:
sin α = y, cos α = x, sin π 2 + α = x, cos π 2 + α = y
sin π 2 + α = cos α, cos π 2 + α = - sin α
Taking into account the basic identities of trigonometry and what has just been proven, we can write
t g π 2 + α = sin π 2 + α cos π 2 + α = cos α - sin α = - c t g α c t g π 2 + α = cos π 2 + α sin π 2 + α = - sin α cos α = - t g α
To prove reduction formulas with argument π 2 - α, it must be presented in the form π 2 + (- α). For example:
cos π 2 - α = cos π 2 + (- α) = - sin (- α) = sin α
The proof uses the properties of trigonometric functions with arguments of opposite signs.
All other reduction formulas can be proven based on those written above.
If you notice an error in the text, please highlight it and press Ctrl+Enter
Reduction formulas are relationships that allow you to go from sine, cosine, tangent and cotangent with angles `\frac (\pi)2 \pm \alpha`, `\pi \pm \alpha`, `\frac (3\pi) 2 \pm \alpha`, `2\pi \pm \alpha` to the same functions of the angle `\alpha`, which is located in the first quarter of the unit circle. Thus, the reduction formulas “lead” us to working with angles in the range from 0 to 90 degrees, which is very convenient.
All together there are 32 reduction formulas. They will undoubtedly come in handy during the Unified State Exam, exams, and tests. But let us immediately warn you that there is no need to memorize them! You need to spend a little time and understand the algorithm for their application, then it will not be difficult for you to derive the necessary equality at the right time.
First, let's write down all the reduction formulas:
For angle (`\frac (\pi)2 \pm \alpha`) or (`90^\circ \pm \alpha`):
`sin(\frac (\pi)2 - \alpha)=cos \ \alpha;` ` sin(\frac (\pi)2 + \alpha)=cos \ \alpha`
`cos(\frac (\pi)2 — \alpha)=sin \ \alpha;` ` cos(\frac (\pi)2 + \alpha)=-sin \ \alpha`
`tg(\frac (\pi)2 — \alpha)=ctg \ \alpha;` ` tg(\frac (\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (\pi)2 — \alpha)=tg \ \alpha;` ` ctg(\frac (\pi)2 + \alpha)=-tg \ \alpha`
For angle (`\pi \pm \alpha`) or (`180^\circ \pm \alpha`):
`sin(\pi - \alpha)=sin \ \alpha;` ` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi - \alpha)=-cos \ \alpha;` ` cos(\pi + \alpha)=-cos \ \alpha`
`tg(\pi - \alpha)=-tg \ \alpha;` ` tg(\pi + \alpha)=tg \ \alpha`
`ctg(\pi - \alpha)=-ctg \ \alpha;` ` ctg(\pi + \alpha)=ctg \ \alpha`
For angle (`\frac (3\pi)2 \pm \alpha`) or (`270^\circ \pm \alpha`):
`sin(\frac (3\pi)2 — \alpha)=-cos \ \alpha;` ` sin(\frac (3\pi)2 + \alpha)=-cos \ \alpha`
`cos(\frac (3\pi)2 — \alpha)=-sin \ \alpha;` ` cos(\frac (3\pi)2 + \alpha)=sin \ \alpha`
`tg(\frac (3\pi)2 — \alpha)=ctg \ \alpha;` ` tg(\frac (3\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (3\pi)2 — \alpha)=tg \ \alpha;` ` ctg(\frac (3\pi)2 + \alpha)=-tg \ \alpha`
For angle (`2\pi \pm \alpha`) or (`360^\circ \pm \alpha`):
`sin(2\pi - \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi - \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi - \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi - \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`
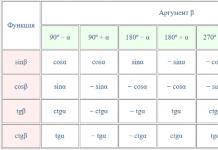
You can often find reduction formulas in the form of a table where angles are written in radians:
To use it, we need to select the row with the function we need and the column with the desired argument. For example, to find out using a table what ` sin(\pi + \alpha)` will be equal to, it is enough to find the answer at the intersection of the row ` sin \beta` and the column ` \pi + \alpha`. We get ` sin(\pi + \alpha)=-sin \ \alpha`.
And the second, similar table, where angles are written in degrees:
Mnemonic rule for reduction formulas or how to remember them
As we already mentioned, there is no need to memorize all the above relationships. If you looked at them carefully, you probably noticed some patterns. They allow us to formulate a mnemonic rule (mnemonic - remember), with the help of which we can easily obtain any reduction formula.
Let us immediately note that to apply this rule you need to be good at identifying (or remembering) the signs of trigonometric functions in different quarters of the unit circle. 
The vaccine itself contains 3 stages:
- The function argument must be represented as `\frac (\pi)2 \pm \alpha`, `\pi \pm \alpha`, `\frac (3\pi)2 \pm \alpha`, `2\pi \ pm \alpha`, and `\alpha` is necessarily an acute angle (from 0 to 90 degrees).
- For the arguments `\frac (\pi)2 \pm \alpha`, `\frac (3\pi)2 \pm \alpha` the trigonometric function of the transformed expression changes to a cofunction, that is, the opposite (sine to cosine, tangent to cotangent and vice versa). For arguments `\pi \pm \alpha`, `2\pi \pm \alpha` the function does not change.
- The sign of the original function is determined. The resulting function on the right side will have the same sign.
To see how this rule can be applied in practice, let’s transform several expressions:
1. `cos(\pi + \alpha)`.
The function is not reversed. The angle `\pi + \alpha` is in the third quarter, the cosine in this quarter has a “-” sign, so the transformed function will also have a “-” sign.
Answer: ` cos(\pi + \alpha)= - cos \alpha`
2. `sin(\frac (3\pi)2 - \alpha)`.
According to the mnemonic rule, the function will be reversed. The angle `\frac (3\pi)2 - \alpha` is in the third quarter, the sine here has a “-” sign, so the result will also have a “-” sign.
Answer: `sin(\frac (3\pi)2 - \alpha)= - cos \alpha`
3. `cos(\frac (7\pi)2 - \alpha)`.
`cos(\frac (7\pi)2 - \alpha)=cos(\frac (6\pi)2+\frac (\pi)2-\alpha)=cos (3\pi+(\frac(\pi )2-\alpha))`. Let's represent `3\pi` as `2\pi+\pi`. `2\pi` is the period of the function.
Important: The functions `cos \alpha` and `sin \alpha` have a period of `2\pi` or `360^\circ`, their values will not change if the argument is increased or decreased by these values.
Based on this, our expression can be written as follows: `cos (\pi+(\frac(\pi)2-\alpha)`. Applying the mnemonic rule twice, we get: `cos (\pi+(\frac(\pi) 2-\alpha)= - cos (\frac(\pi)2-\alpha)= - sin \alpha`.
Answer: `cos(\frac (7\pi)2 - \alpha)=- sin \alpha`.
Horse rule
The second point of the mnemonic rule described above is also called the horse rule of reduction formulas. I wonder why horses?
So, we have functions with arguments `\frac (\pi)2 \pm \alpha`, `\pi \pm \alpha`, `\frac (3\pi)2 \pm \alpha`, `2\pi \ pm \alpha`, points `\frac (\pi)2`, `\pi`, `\frac (3\pi)2`, `2\pi` are key, they are located on the coordinate axes. `\pi` and `2\pi` are on the horizontal x-axis, and `\frac (\pi)2` and `\frac (3\pi)2` are on the vertical ordinate.
We ask ourselves the question: “Does a function change into a cofunction?” To answer this question, you need to move your head along the axis on which the key point is located.
That is, for arguments with key points located on the horizontal axis, we answer “no” by shaking our heads to the sides. And for corners with key points located on the vertical axis, we answer “yes” by nodding our heads from top to bottom, like a horse :)
We recommend watching a video tutorial in which the author explains in detail how to remember reduction formulas without memorizing them.
Practical examples of using reduction formulas
The use of reduction formulas begins in grades 9 and 10. Many problems using them were submitted to the Unified State Exam. Here are some of the problems where you will have to apply these formulas:
- problems to solve a right triangle;
- transformation of numeric and alphabetic trigonometric expressions, calculation of their values;
- stereometric tasks.
Example 1. Calculate using reduction formulas a) `sin 600^\circ`, b) `tg 480^\circ`, c) `cos 330^\circ`, d) `sin 240^\circ`.
Solution: a) `sin 600^\circ=sin (2 \cdot 270^\circ+60^\circ)=-cos 60^\circ=-\frac 1 2`;
b) `tg 480^\circ=tg (2 \cdot 270^\circ-60^\circ)=ctg 60^\circ=\frac(\sqrt 3)3`;
c) `cos 330^\circ=cos (360^\circ-30^\circ)=cos 30^\circ=\frac(\sqrt 3)2`;
d) `sin 240^\circ=sin (270^\circ-30^\circ)=-cos 30^\circ=-\frac(\sqrt 3)2`.
Example 2. Having expressed cosine through sine using reduction formulas, compare the numbers: 1) `sin \frac (9\pi)8` and `cos \frac (9\pi)8`; 2) `sin \frac (\pi)8` and `cos \frac (3\pi)10`.
Solution: 1)`sin \frac (9\pi)8=sin (\pi+\frac (\pi)8)=-sin \frac (\pi)8`
`cos \frac (9\pi)8=cos (\pi+\frac (\pi)8)=-cos \frac (\pi)8=-sin \frac (3\pi)8`
`-sin \frac (\pi)8> -sin \frac (3\pi)8`
`sin \frac (9\pi)8>cos \frac (9\pi)8`.
2) `cos \frac (3\pi)10=cos (\frac (\pi)2-\frac (\pi)5)=sin \frac (\pi)5`
`sin \frac (\pi)8 `sin \frac (\pi)8 Let us first prove two formulas for the sine and cosine of the argument `\frac (\pi)2 + \alpha`: ` sin(\frac (\pi)2 + \alpha)=cos \ \alpha` and ` cos(\frac (\ pi)2 + \alpha)=-sin \ \alpha`. The rest are derived from them. Let's take a unit circle and point A on it with coordinates (1,0). Let after turning to Coming from the definition of tangent and cotangent, we obtain ` tan(\frac (\pi)2 + \alpha)=\frac (sin(\frac (\pi)2 + \alpha))(cos(\frac (\pi)2 + \alpha))=\frac (cos \alpha)(-sin \alpha)=-ctg \alpha` and ` сtg(\frac (\pi)2 + \alpha)=\frac (cos(\frac (\ pi)2 + \alpha))(sin(\frac (\pi)2 + \alpha))=\frac (-sin \alpha)(cos \alpha)=-tg \alpha`, which proves the reduction formulas for tangent and the cotangent of the angle `\frac (\pi)2 + \alpha`. To prove formulas with the argument `\frac (\pi)2 - \alpha`, it is enough to represent it as `\frac (\pi)2 + (-\alpha)` and follow the same path as above. For example, `cos(\frac (\pi)2 - \alpha)=cos(\frac (\pi)2 + (-\alpha))=-sin(-\alpha)=sin(\alpha)`. The angles `\pi + \alpha` and `\pi - \alpha` can be represented as `\frac (\pi)2 +(\frac (\pi)2+\alpha)` and `\frac (\pi) 2 +(\frac (\pi)2-\alpha)` respectively. And `\frac (3\pi)2 + \alpha` and `\frac (3\pi)2 - \alpha` as `\pi +(\frac (\pi)2+\alpha)` and `\pi +(\frac (\pi)2-\alpha)`. They belong to the trigonometry section of mathematics. Their essence is to reduce trigonometric functions of angles to a “simple” form. Much can be written about the importance of knowing them. There are already 32 of these formulas! Don’t be alarmed, you don’t need to learn them, like many other formulas in a math course. There is no need to fill your head with unnecessary information, you need to remember the “keys” or laws, and remembering or deriving the required formula will not be a problem. By the way, when I write in articles “... you need to learn!!!” - this means that it really needs to be learned. If you are not familiar with reduction formulas, then the simplicity of their derivation will pleasantly surprise you - there is a “law” with the help of which this can be easily done. And you can write any of the 32 formulas in 5 seconds. I will list only some of the problems that will appear on the Unified State Exam in mathematics, where without knowledge of these formulas there is a high probability of failing in solving them. For example: – problems for solving a right triangle, where we are talking about the external angle, and problems for internal angles, some of these formulas are also necessary. – tasks on calculating the values of trigonometric expressions; converting numerical trigonometric expressions; converting literal trigonometric expressions. – problems on the tangent and the geometric meaning of the tangent, a reduction formula for the tangent is required, as well as other problems. – stereometric problems, in the course of solving it is often necessary to determine the sine or cosine of an angle that lies in the range from 90 to 180 degrees. And these are just those points that relate to the Unified State Exam. And in the algebra course itself there are many problems, the solution of which simply cannot be done without knowledge of reduction formulas. So what does this lead to and how do the specified formulas make it easier for us to solve problems? For example, you need to determine the sine, cosine, tangent, or cotangent of any angle from 0 to 450 degrees: the alpha angle ranges from 0 to 90 degrees * * *
So, it is necessary to understand the “law” that works here: 1. Determine the sign of the function in the corresponding quadrant. Let me remind you: 2. Remember the following: function changes to cofunction
function does not change to cofunction
What does the concept mean - a function changes to a cofunction?
Answer: sine changes to cosine or vice versa, tangent to cotangent or vice versa.
That's all! Now, according to the presented law, we will write down several reduction formulas ourselves: This angle lies in the third quarter, the cosine in the third quarter is negative. We don’t change the function to a cofunction, since we have 180 degrees, which means: The angle lies in the first quarter, the sine in the first quarter is positive. We do not change the function to a cofunction, since we have 360 degrees, which means: Here is another additional confirmation that the sines of adjacent angles are equal: The angle lies in the second quarter, the sine in the second quarter is positive. We do not change the function to a cofunction, since we have 180 degrees, which means: Work through each formula mentally or in writing, and you will be convinced that there is nothing complicated. ***
In the article on the solution, the following fact was noted - the sine of one acute angle in a right triangle is equal to the cosine of another acute angle in it.
angle `\alpha` it will go to point `A_1(x, y)`, and after turning by angle `\frac (\pi)2 + \alpha` to point `A_2(-y, x)`. Dropping the perpendiculars from these points to the line OX, we see that the triangles `OA_1H_1` and `OA_2H_2` are equal, since their hypotenuses and adjacent angles are equal. Then, based on the definitions of sine and cosine, we can write `sin \alpha=y`, `cos \alpha=x`, `sin(\frac (\pi)2 + \alpha)=x`, `cos(\frac (\ pi)2 + \alpha)=-y`. Where can we write that ` sin(\frac (\pi)2 + \alpha)=cos \alpha` and ` cos(\frac (\pi)2 + \alpha)=-sin \alpha`, which proves the reduction formulas for sine and cosine angles `\frac (\pi)2 + \alpha`.
