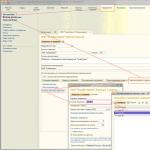
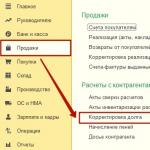
Man is able to see through light. Light quanta - photons have the properties of both waves and particles. Light sources are divided into primary and secondary. In primary - such as the Sun, lamps, fire, electric discharge - photons are born as a result of chemical, nuclear or thermonuclear reactions.

Any atom serves as a secondary source of light: having absorbed a photon, it goes into an excited state and sooner or later returns to the main one, emitting a new photon. When a beam of light hits an opaque object, all of the photons that make up the beam are absorbed by the atoms on the surface of the object.

Excited atoms almost immediately return the absorbed energy in the form of secondary photons, which are evenly radiated in all directions.

If the surface is rough, then the atoms on it are arranged randomly, the wave properties of light do not appear, and the total radiation intensity is equal to the algebraic sum of the radiation intensity of each re-emitting atom. In this case, regardless of the viewing angle, we see the same light flux reflected from the surface - such a reflection is called diffuse. Otherwise, light is reflected from a smooth surface, such as a mirror, polished metal, glass.

In this case, the atoms re-emitting light are ordered relative to each other, the light exhibits wave properties, and the intensities of the secondary waves depend on the phase differences of neighboring secondary light sources. As a result, the secondary waves compensate each other in all directions, with the exception of a single one, which is determined by a well-known law - the angle of incidence is equal to the angle of reflection.
Photons seem to rebound elastically from the mirror, so their trajectories go from objects that are, as it were, behind it - they are what a person sees when looking into the mirror. True, the looking-glass world is different from ours: the texts are read from right to left, the clock hands are spinning in the opposite direction, and if you raise your left hand, our double in the mirror will raise his right, and the rings are on the wrong hand ... Unlike the movie screen, where all the spectators they see the same image, the reflections in the mirror are different for everyone.

For example, the girl in the picture does not see herself in the mirror at all, but the photographer (since he sees her reflection). To see yourself, you need to sit in front of the mirror. Then the photons coming from the face in the direction of gaze fall on the mirror almost at a right angle and come back.

When they reach your eyes, you see your image on the other side of the glass. Closer to the edge of the mirror, the eyes catch photons reflected by it at a certain angle. This means that they also came at an angle, that is, from objects located on either side of you. This allows you to see yourself in the mirror along with the surroundings.

But less light is always reflected from the mirror than it falls, for two reasons: there are no perfectly smooth surfaces, and the light always heats the mirror a little. Of the widely used materials, polished silver reflects light best (more than 95%).
Mirrors were made from it in ancient times. But in the open air, silver tarnishes due to oxidation, and the polish is damaged. In addition, a metal mirror is expensive and heavy.

Now a thin layer of metal is applied to the back of the glass, protecting it from damage with several layers of paint, and aluminum is often used instead of silver to save money. Its reflectance is about 90%, and the difference is imperceptible to the eye.

Why do we see the reflection in the mirror?

Man is able to see through light. Light quanta - photons have the properties of both waves and particles. Light sources are divided into primary and secondary. In the primary - such as the Sun, lamps, fire, electric discharge - photons are born as a result of chemical, nuclear or thermonuclear reactions.

Any atom serves as a secondary source of light: having absorbed a photon, it goes into an excited state and sooner or later returns to the main one, emitting a new photon. When a beam of light hits an opaque object, all of the photons that make up the beam are absorbed by the atoms on the surface of the object. Excited atoms almost immediately return the absorbed energy in the form of secondary photons, which are evenly radiated in all directions. If the surface is rough, then the atoms on it are arranged randomly, the wave properties of light do not appear, and the total radiation intensity is equal to the algebraic sum of the radiation intensity of each re-emitting atom.

In this case, regardless of the viewing angle, we see the same light flux reflected from the surface - such a reflection is called diffuse. Otherwise, light is reflected from a smooth surface, such as a mirror, polished metal, glass. In this case, the atoms re-emitting light are ordered relative to each other, the light exhibits wave properties, and the intensities of the secondary waves depend on the phase differences of neighboring secondary light sources.

As a result, the secondary waves compensate each other in all directions, except for one single one, which is determined according to a well-known law - the angle of incidence is equal to the angle of reflection. Photons seem to rebound elastically from the mirror, so their trajectories go from objects that are, as it were, behind it - they are what a person sees when looking into the mirror. True, the looking-glass world is different from ours: the texts are read from right to left, the clock hands turn in the opposite direction, and if you raise your left hand, our double in the mirror will raise his right, and the rings are on the wrong hand ... Unlike the movie screen, where All viewers see the same image, reflections in the mirror are different for everyone. For example, the girl in the picture does not see herself in the mirror at all, but the photographer (since he sees her reflection).

To see yourself, you need to sit in front of the mirror. Then the photons coming from the face in the direction of gaze fall on the mirror almost at a right angle and come back. When they reach your eyes, you see your image on the other side of the glass. Closer to the edge of the mirror, the eyes catch photons reflected by it at a certain angle. This means that they also came at an angle, that is, from objects located on either side of you. This allows you to see yourself in the mirror along with the surroundings.

But less light is always reflected from the mirror than it falls, for two reasons: there are no perfectly smooth surfaces, and the light always slightly heats the mirror. Of the widely used materials, polished silver reflects light best (more than 95%). Mirrors were made from it in ancient times. But in the open air, silver tarnishes due to oxidation, and the polish is damaged. In addition, a metal mirror is expensive and heavy. Now a thin layer of metal is applied to the back of the glass, protecting it from damage with several layers of paint, and aluminum is often used instead of silver to save money. Its reflectance is about 90%, and the difference is imperceptible to the eye.

HOW DOES A MIRROR REFLECT?

Of course, we all know how a mirror reflects, but if it is necessary to describe it exactly, difficulties will undoubtedly arise. As a rule, we are satisfied with ourselves if we imagine something at least “in principle”. And the details that physics teachers explained to us on the blackboard with the help of chalk and a ruler, every normal schoolboy and student tries to forget, and the sooner the better.

Every child, full of surprise at the world around him, will certainly be interested in how the mirror reflects him. But adults usually answer in such cases: "Don't ask stupid questions!" A person droops, begins to be shy, his surprise gradually fades, and he tries not to show it again for the rest of his life (which is a pity!).

But in this book we will be as surprised as possible, remembering the words of Bertolt Brecht: “There are no stupid questions, there are only stupid answers.”

What is the shortest route from the burning house to the fire station? The "angle of incidence" at which the fire engine reaches the river must be equal to the "angle of reflection" at which it will rush towards the fire.

Of course, people can be divided into fools and smart, big and small, they differ in language, religion, worldview. You can also imagine a division like this:

1) people who are never surprised;

2) people who are surprised, but do not think about the phenomenon that surprised them;

3) people who, surprised, ask “why?”;

4) people who, surprised, turn to number and measure.

Depending on the living conditions, traditions, degree of education, there are also all possible "intermediate" steps. The thinkers of antiquity and the Middle Ages were amazed at the world and thought about its mysteries. But they only occasionally had a chance to measure any phenomenon.

Only in the Renaissance, that is, in the 16th century, people came to the conclusion that measurement is better than blind faith or scholastic reasoning. This was facilitated by economic interests, which could only be satisfied through the development of the natural sciences, through quantitative measurements. (We see that, in essence, exchange value was "measured" with the help of money.) For the 16th century. optics was cutting edge science. From a glass ball filled with water, which was used as a focusing lens, a magnifying glass arose, and from it a microscope and a telescope. The Netherlands, the largest maritime power in those days, needed good telescopes for the fleet in order to see the dangerous coast ahead of time or get away from the enemy in time. Optics ensured the success and reliability of navigation. Therefore, it was in the Netherlands that many scientists were engaged in it. The Dutchman Willebrord, Snell van Rooyen, who called himself Snellius (1580-1626), observed (which, by the way, many before him had seen) how a thin beam of light was reflected in a mirror. He simply measured the angle of incidence and the angle of reflection of the beam (which no one had done before him) and established the law: the angle of incidence is equal to the angle of reflection.

Now, in hindsight, this law seems to us something taken for granted. But in those days it had a huge, one might say, ideological significance, which awakened philosophical thought until the 19th century.

Let's set ourselves the following mathematical problem: a fire broke out in some house. The fire brigade is called, and water for extinguishing has to be taken from the river. Where should you pick it up in order to get it to the burning house as quickly as possible?

The answer is: the place must be chosen in such a way that the angle of approach to the river is equal to the angle of departure from it in a straight line to the burning house. In this case, the total length of the path segments will be minimal. (Such a principle of minimum-maximum was previously considered as a manifestation of the "will of God").

Snell's law of reflection explains the phenomenon of specular reflection, to which it should only be added why it is characteristic only of shiny and smooth surfaces. In fact, rough surfaces also obey the law of reflection. But due to their roughness, they seem to consist of small mirrors, haphazardly directed in all directions. In addition, the material that we consider as a mirror must absorb light to a very small extent and not be transparent. Such qualities are distinguished, for example, by polished metals, calm water over a dark bottom, some polished stones and, above all, glass placed on an opaque substrate.

Each point of the object corresponds to its reflection in the mirror, and therefore in it our right eye moves to the left side. As a result of this transfer of points, objects located farther away in the mirror also appear to be reduced in accordance with the laws of perspective. Technically, we can reconstruct the mirror image as if it were located behind the glass surface. But this is only an apparent perception. It is no coincidence that animals and small children often look behind the mirror; they believe that the image lurks behind, like a picture seen outside a window. The fact of the reversal of left and right is correctly realized only by adults.

MIRROR WITH CONVEYOR

One of the Greek myths tells of Narcissus, who lay for hours on the shore of the lake, admiring his reflection in the water.

If Narcissus were a wealthy man, he would probably have bought himself a polished metal mirror. In those days, it was not so easy to bring a piece of steel or bronze the size of a palm to a mirror shine. In addition, the surface of such a mirror oxidized and had to be cleaned daily. The Latin spectrum in German has become Spiegel ("Spiegel" - a mirror). From which we can conclude that the Romans brought mirrors to Germany.

Only in the XI century. glass mirrors known to us appeared. One of the first mentions of them belongs to the French minstrel Vensant de Beauvais. According to him, in such mirrors, lead was superimposed on the glass from below. Obviously, it is unnecessary to comment on the context in which the minstrel mentions the mirror. And in 1773 in Nuremberg there was already a shop of mirror-makers. Since that time, the manufacture of mirrors has become an important branch of European crafts.

Venice was the first country (at that time it had the status of an independent state), which began to issue patents for inventions. In 1507, the Danzalo del Gallo brothers received a patent for the manufacture of crystal mirrors. Today, in the antiques market, Venetian mirrors are a treasure. In those days, thin tin foil was placed under the glass plate (tin is easily rolled on rolls). Mercury was poured onto the foil, which formed an amalgam with tin. Since mercury vapor is very toxic, this method was banned a long time ago and replaced by silvering.

In a rectangular corner mirror (at an angle between the mirrors of 90°), the positions "right" and "left" are preserved

For a long time, the technique of protecting a thin metal layer with a varnish coating has been preserved. Today, sheet glass moves along a conveyor, where a silver salt solution and a reducing agent are successively applied to its surface from spray guns, which precipitates pure silver from the solution in a finely dispersed (colloidal) form; after that, a layer of copper is applied on a thin layer of silver, protecting the silver film, and finally both metals are varnished. The conveyor belt moves at a speed of about 2.5 m/min. The monthly production of such a unit is about 40,000 m2 of mirror. If some too "smart" reader intends to scrape silver from a large wall mirror to decorate his wife or friend, then it is useful for him to know that the layer of silver on the mirror is so thin that "the game is not worth the candle." Less than 1 g of silver is deposited on 1 m 2 of the mirror surface.

Glass making was once considered a great art. There was a story that in the time of the Roman emperor Tiberius (42 BC), someone discovered safety glass. Tiberius ordered the execution of this man so that his discovery would not lead to the depreciation of the glass. Today, inventors working in the glass industry need not fear a similar fate. On the contrary, all efforts are reduced to making glass as cheap as possible.

Among solid substances of inorganic origin (stone, metal), glass occupies a special place. Strictly speaking, certain properties of glass bring it closer to a liquid. Most substances in solid and liquid state behave differently. The easiest way to observe water and ice. Water is in droplet-liquid form. At exactly 0°C, pure water begins to crystallize. The solidification temperature remains zero until all the water turns into ice. Even in the Arctic, with a frost of -50 ° C, the water under the ice maintains a temperature of 0 ° C. Only when all the water is gone can the ice be cooled further. Ice as a solid body has a crystalline structure. Within its small patches, the crystals, we find a distinct symmetry. This symmetry is recognized on x-rays (radiographs).

Glass is another matter. There are no crystals in it. There is no sharp transition in it at a certain temperature from a liquid state to a solid state (or vice versa). Molten glass (glass mass) remains solid over a wide range of temperatures. If we take the viscosity of water as 1, then the viscosity of molten glass at 1400°C is 13,500. If glass is cooled to 1000°C, it becomes malleable and 2 million times more viscous than water. (For example, a loaded glass tube or sheet sags over time.) At an even lower temperature, the glass turns into a liquid of infinitely high viscosity.

The main component of glasses is silicon dioxide, or silica, - SiO 2. In its purest form, it is represented in nature by white quartz sand. Silicon dioxide crystallizes relatively gradually during the transition from the melt to the solid state. A quartz melt can be cooled below its solidification temperature without becoming solid. There are many other liquids and solutions that can also be supercooled. But only quartz lends itself to supercooling so much that it loses its ability to form crystals. The silicon dioxide then remains "free of crystals", i.e. "liquid".

It would be too expensive to process pure quartz, primarily because of its relatively high melting point. Therefore, technical glasses contain only 50 to 80% silicon dioxide. To lower the melting point, additives of sodium oxide, alumina, and lime are introduced into the composition of such glasses. Obtaining certain properties is achieved by adding some more chemicals. The famous lead glass, which is carefully polished in the manufacture of bowls or vases, owes its brilliance to the presence of about 18% lead in it.

Mirror glass contains predominantly cheap components that lower the melting point. In large baths (as glass makers call them), containing more than 1000 tons of glass, low-melting substances are first melted. Molten soda and other chemicals dissolve quartz (like water dissolves salt). By such a simple means, it is possible to convert silicon dioxide into a liquid state already at a temperature of about 1000 ° C (although in its pure form it begins to melt only at much higher temperatures). To the great annoyance of glassmakers, gases are released from the glass melt. At 1000°C, the melt is still too viscous for the free exit of gas bubbles. For degassing, it should be brought to a temperature of 1400-1600°C. Such high temperatures are reached in the so-called regenerative glass furnaces, invented in 1856 by Friedrich Siemens. In them, the exhaust gases are heated by preheating chambers lined with refractory materials. As soon as these chambers are hot enough, combustible gases and the air necessary for their combustion are supplied to them. The gases that arise during combustion evenly mix the molten glass, otherwise it would be far from easy to mix a thousand tons of viscous melt.

The modern glass melting furnace is a continuous furnace. From one side, the initial substances are fed into it, which, due to a slight inclination, move, gradually turning into molten glass, towards the opposite side (the distance between the walls of the furnace is about 50 m). There, a precisely measured portion of the finished glass enters the cooled rolls. A glass ribbon several meters wide stretches along the entire length of the hundred-meter cooling section. At the end of this section of the machine, it is cut into sheets of the desired format and size for mirrors or window glass.

The hardness of glass is known (in German there is even an expression "hard as glass"). In Pushkin's poem "Eugene Onegin", Tatyana in love carves on the window glass an expensive name with a diamond ring ( Apparently, the author is familiar with Pushkin's translation. In the original, Tatyana "wrote with a pretty finger on a misted glass." - Note, translation). Today, "diamonds" for cutting glass are made from synthetic stones or hard alloys. Glass is also distinguished by a fair amount of compressive strength. This property is used to create stained-glass windows, decorative partitions. In contrast, the tensile strength of glass is negligible. High-strength glasses are a novelty today. Among other applications, they are used for pipelines in the chemical industry. Transparency is also important for a mirror. Normal glass transmits 70 to 90% of visible light. The transparency of glass remains an indispensable condition for the manufacture of good mirrors. For ultraviolet light (≈ 10 15 -10 16 Hz), glass is not transparent. In the first days of spring, when it is still cold, but the sun begins to warm up, there are fanatical tanners who sit by the windows, exposing their faces to the sun's rays. But all their efforts are in vain if special glasses are not inserted into the frames, transparent to ultraviolet rays.

Those who have several mirrors in their apartment must have noticed that their quality is different. First of all, a good mirror should not have streaks that distort the image. Such streaks occur due to incomplete melting of glass or uneven cooling.

The brilliance of a mirror can be improved both by the composition of the glass and by careful surface treatment (grinding and polishing).

And yet it is amazing: just as Narcissus in ancient times, lying on the shore of a lake, admired his reflection in the water, so we, modern people, look into mirrors, which are essentially a “liquid”!

However, in the future, the production of mirrors will most likely follow the path of using a plastic film on which a thin layer of metal is deposited.

FROM TRILLAGE TO RADAR

Of course not: it is enough to reflect the mirror image a second time in the mirror in order to see your true face. Often in houses there are still so-called trellises. They have one large main mirror in the center and two smaller mirrors on the sides. Many people think that these side mirrors serve only to look at the curls behind the ears. But if such a side mirror is placed at right angles to the middle one, then you can see yourself exactly in the form in which others see you. Close your left eye, and your reflection in the second mirror will repeat your movement with your left eye. Before trellis, you can choose whether you want to see yourself in a mirror image or in a direct image.

A corner mirror with a right angle between its constituent mirrors has some other interesting properties. If you make it from two small mirrors, you can see for yourself that in such a mirror with a rectangular solution (and now we are talking only about it), the reflected beam of light is always parallel to the incident beam. This is a very important property. But not the only one! When the corner mirror is rotated around the axis connecting the mirrors (within certain limits), the reflected beam will not change its direction.

In technology, mirrors are usually not made up, but a rectangular prism is used, in which the corresponding faces provide a mirror beam path.

Rectangular prisms, as if "folding" the path of the beam like an "accordion", while maintaining its required length, given by the focal length of the lens, make it possible to reduce the dimensions of optical devices. In prismatic binoculars, the light rays with the help of such devices turn 180 °.

In old paintings, you can see captains and generals with exorbitantly long spyglasses. Angled mirrors have transformed old spyglasses into modern binoculars.

Billiards players have long been familiar with the action of reflection. Their "mirrors" are the sides of the playing field, and the trajectories of the balls play the role of a beam of light. Having hit the side near the corner, the ball rolls to the side located at a right angle, and, reflected from it, moves back parallel to the direction of the first impact.

The property of the reflected beam to maintain direction when the corner mirror rotates around its axis is widely used in technology. So, in a trihedral mirror corner reflector, the beam maintains a constant direction, despite the very strong oscillations of the mirror. In shape, such a mirror is a cube with a cut off corner. And in this case, in practice, not three mirrors are used, but the corresponding glass prism with mirror edges.

An important area of ​​application of a trihedral mirror is a corner reflector (cat's eye, reflector) on bicycles, motorcycles, signal safety boards, roadway limiters. From whichever side the light falls on such a reflector, the light reflection always retains the direction of the light source.

Trihedral mirror corner reflectors play an important role in radar technology. Airplanes and large steel ships reflect the radar beam. Despite its significant scattering, that small fraction of the reflected radio waves that returns to the radar is usually enough to recognize the object.

The situation is worse with small boats, signal floats and plastic sailing yachts. For small objects, the reflection is too weak. Plastic yachts are as "transparent" to radio waves, which operate radar technology, as window panes are to sunlight. Therefore, sailing yachts and signal buoys are equipped with metal corner reflectors. The length of the edges of such a "mirror" is only about 30 cm, but this is enough to return a sufficiently powerful echo.

Let's return once again to the corner mirror of two connected mirrors. Let's swing its axis to the right or to the left - our image will also tilt to the side. We can even lay it down if we place the axis of the mirror horizontally. But by tilting the mirror even further, we will notice that the image "straightens out". Of course, and we will look for an explanation for this. It fits perfectly with the theme of this book.

The corner mirror has a plane of symmetry that bisects the space between both mirrors. With an appropriate form, it can have another plane perpendicular to the mirrors, but we will not consider it here. We are only interested in the plane of symmetry passing between the mirrors in which, so to speak, both mirrors are mutually reflected.

Each plane of symmetry changes, as we already know, right to left (and vice versa). But this is a somewhat simplified perception. If the plane of symmetry could speak, it would say, “I don’t change right to left, or up to down. I don't even know what it is. I only display dot by dot everything that is on one side or the other of me. If a person with his longitudinal axis stands parallel to his axis, I will change his right and left sides, but if the same person with his longitudinal axis is perpendicular to my axis (for I always remain unchanged), then I will change what people call top and bottom " . As you can see, it all depends on the point of view.

But in the end, what can be measured and counted is true. Today, we don't see much achievement in Snell's measuring the angles of incidence and reflection of the beam. But we must not forget that the scientists of the XVI century. such discoveries broke more than twenty centuries of tradition.

Among the secrets of television, a trick is known to reduce the performer, who, against the background of the entire environment, “life-size” looks like a small doll. Sometimes the viewer can see the actor at the same time in two scales: in the foreground at the usual size, and in the background at a reduced size.

Anyone who is experienced in photography understands how such an effect is achieved. First, a reduced version is filmed, and then the actor plays in front of a screen onto which his reduced image is projected.

The famous "magician" Jochen Zmeck in his fascinating book "The Magical World of Magic" ( Zmeck J. Wunderwelt Magie. Berlin: Heuchel-Verlag, Kunst und Gesellschaft, 1974) describes how such miracles can be done without photography. When a reduced object should appear in space by itself, with the help of a concave mirror, its image is projected in such a way that it appears to be standing on a stand.

Illusionist Alexander Furst built this trick as follows. The viewer saw a small stage with greatly reduced artists. In order to project them in this form onto a screen, Furst used an angled mirror in his construction. It was in front of him that the artists moved. But the mirror turned them over by 180° and thus put them “on their heads”, and this image was already turned over by the concave mirror and thrown onto a small stage. An indispensable condition for the effect was the impeccable cleanliness of all mirrors.

Of course, the “magician” could demonstrate not only the appearance of some objects, but also their lightning-fast disappearance, as soon as he uttered the magical “simsalabim” (and, of course, turn off the light source or turn off the mirror). How charming such a Tanagra theater (as such spectacles are called) can be seen by looking through inverted binoculars. Reduced, as if concentrated world looks very interesting in it. The principle of operation of both prismatic binoculars and the Tanagra theater is the same. Only in one case lenses are used, and in the other case a concave mirror is used.

ABOUT LEFT-HANDED AND RIGHT-HANDED

Now that we know how mirrors work and how they are made, let's think a little more about what we see in a mirror in our daily life.

It can turn into a hobby: analyze every object in terms of symmetry. Recall that if you cut an object along its plane of symmetry and put one of the halves perpendicular to the mirror, then the second, “cut off” half will appear in the mirror. Therefore, whether we are talking about a mirror or a plane of symmetry, we are talking, in essence, about phenomena of the same order.

In principle, all possible "magic" optical tricks are based on the "seamless" transition of an image into its mirror reflection. You can easily comprehend and reproduce the secret of the “lady cut in half” and other similar tricks using a trellis consisting of several mirrors. Turn one of the small mirrors inwards so that it can be clearly seen in the large mirror. Place your hand on the edge of a small mirror so that your middle finger is parallel to the edge, and you will see in the mirror that your hand consists of two little fingers and two ring fingers. Stick out your little finger, and two fingers move in the mirror. A little imagination - and this "number" can be prepared for demonstration at home evening. The condition for success here, as in a variety show or a circus, is the impeccable cleanliness of the mirror. A good and large enough mirror (so that its edges are not visible) is not noticeable to the eyes.

Buckets are always produced with the expectation that they will be taken with the right hand. But every left-hander would prefer a ladle in a "mirror" design

After we mentally separate chairs, tables, vases, people, animals, houses and trees by planes of symmetry, we, of course, want to look for asymmetric bodies.

We have already mentioned spiral staircases and spiral threading. Perhaps, we should once again clarify the property of asymmetry: it is impossible to draw a symmetry plane through an asymmetric object ( The author here refers to symmetric only those bodies that have planes of symmetry. In the modern doctrine of symmetry, all figures consisting of equal regularly repeating parts are referred to as symmetrical bodies. In particular, figures with helical lines, considered as infinitely extended systems, have helical axes of symmetry, that is, they are considered symmetrical. - Approx. ed). Therefore, it cannot be “correctly” reflected in the mirror. And vice versa: each spiral twists in the mirror "in the other direction." The left turn becomes right. The left hand turns into the right. Maybe that's where the words "left-handed" and "right-handed" come from?

However, an objection may arise here: how can a person, a creature endowed with a plane of symmetry, “swap” hands or ears in a mirror ?!

In order to understand, imagine that only a hand is visible in the mirror, without its owner. You can try it yourself, standing sideways to the mirror, place one hand in front of it. Or just take a close look at your gloves. They relate to each other like an image and its mirror image. But if you cut a cube in the middle, you will not distinguish the halves! They are combined (mentally) without any difficulty.

The surface of the cup is symmetrical: you can drink from it both on the right and on the left. But our grandfathers used special cups for barbels. From above, such a cup had a visor so that a proud mustache would not be dipped in coffee. The hole through which they filled the cup and drank was on one side. This cup is no longer symmetrical. It was made either for the left or right hand.

Scissors are usually made for the right hand. You will immediately notice this as soon as you try to cut a nail on it, with scissors in your left hand. Buckets are also always made for the right hand. Among souvenir trifles, corkscrews for the left hand are sometimes sold as a curiosity: after all, it is very inconvenient for a left-hander to open a bottle with a normal corkscrew. Asymmetric, of course, are such objects as the propeller of a ship or aircraft. Previously, large seaplanes had two propellers: a pusher and a puller. It is not difficult to imagine how they revolved. Or take, for example, a pencil sharpener in your right hand, and rotate the lead with your left. You will immediately notice that there is asymmetry here as well.

Finally, look at guitars, violins, and other stringed instruments. They are symmetrical (if you do not take into account the thickness of the strings and the location of the pegs). But the whole system of violin and bow is asymmetric. It would be interesting to know if there are left-handers among violinists!

CHARLIE CHAPLIN AND SEA KNOTES

And great people have their problems. A very important question for a public figure: where to put your hands? In The Great Dictator, the consummate Charlie Chaplin tries to find a solution to this problem before showing himself to the people. He stands in front of a mirror. Of course, it would be best to just put your hands in your pockets. But you can not drop your dignity! And so Chaplin goes through all conceivable positions. Finally, he crosses his arms over his chest in a pose, in his opinion, the most impressive of his contemporaries.

Looking at paintings, monuments or ceremonial portraits, it is easy to see that there are only a few spectacular hand positions. But for us, only crossed arms are of interest. If you don't hesitate to try this, you will find that there are two options. Your right hand lies down so that its brush is hidden under the left forearm. Or vice versa: the right hand lies on the left forearm, and the left is hidden under the right hand.

The straight sea knot is symmetrical. Asymmetric "women's knot"

Imagine that these are not hands, but shoelaces. They can also be flipped from left to right or right to left.

In the language of sailors, such a simple connection is called a "half bayonet." If you can't believe you've tied your limbs in a knot, ask to be given one end of a rope in each of your crossed arms. Now take your hands out of your armpits - there will be a “half-bayonet” knot on the rope.

To this “half” of the knot, naturally, the second half should be added to make a solid knot. But if you try to do this, be careful! There are two possible options here. If you "correctly" lay the ends of the rope, you will get a "flat bayonet" knot. As soon as you put them “wrong”, you will end up with a “woman's knot” that inspires disgust in every sailor. The "Baby knot" is tightened tightly, and it is very difficult to untie it. The "flat bayonet" is also tightly tightened, but it is very easy to untie it, you just have to move the corresponding ends towards each other. For us, in both cases, there is another significant difference: the “flat bayonet” is symmetrical, and the “woman's knot” is asymmetrical.

But back to Charlie Chaplin. Both crossed arms (or ends of the rope) essentially reproduce the turns of the screw and are devoid of symmetry. Therefore, intertwined ends and it is impossible to mentally translate one into the other. They relate like an image and its mirror image. And if you tie a “half-bayonet” in front of a mirror, your reflection in the mirror will tie it “in reverse”. In order for a correct sea knot to be obtained after the second overlap, it must be tied in a mirror image with respect to the first.

Ropes or cables can be twisted from left to right or right to left. There are ropes (and cables) twisted from right to left along the letter Z and twisted from left to right along the letter S. This refers to the long middle element of the letter, directed along the fibers of the rope. The arrangement of these elements in letters is mirrored in relation to each other, which applies to the same extent to the corresponding ropes.

Do these young people know that they have "tied" their hands in front of each other with a left and right knot?

However, if you begin to look at your clothesline, it may turn out that it is not retinue at all, but woven. Twisted ropes stretch under load, and woven ropes almost do not. (A clothesline that stretches when wet clothes are hung on it is not very convenient!) It is interesting, by the way, that the snail curls its house in a Z-shaped coil.

In a special book on sea knots, we find about 4,000 different rope tying problems. Many of these knots are very attractive to look at, but hopelessly asymmetrical.

In the pictures depicting old sailing ships, you can see how the sailors climb the masts on the rope ladders. For sailors, this is called "climbing the shrouds." Guys are long ropes or cables that stretch from the sides of the ship to the mast. Rope "crossbars" are attached to them. These short pieces of tackle must be attached "tightly" (in no case with a "flat bayonet" knot!). How such a fastening looks like is shown in the figure. At first glance, it seems symmetrical, but it is not. All sorts of decorative knots produce the same impression. They can be found both in art products and on military uniforms.

The flat bayonet nautical knot gives us another great example of symmetry. Here it is necessary to consider not only the symmetry of the form, but also the symmetry of the load. Our cross knot can be tied (correctly!) in such a way that the ends of the rope are first tied together, which subsequently must be stressed. But you can also tie it in such a way that the loaded end is connected to the free, unloaded ("self-opening" knot). In the tied form, both knots are practically indistinguishable. However, if you load an incorrectly tied knot, then it will not hold. As the sailors say, the knot will “break apart”.

It is he who is used in their performances by magicians and illusionists. Earlier, when hammocks still existed on ships, there were always helpful assistants to fasten a hammock to a beginner. Naturally, in the middle of the night, the gullible newcomer ended up on the floor.

Mathematicians and engineers often have to deal with knots and solve related problems. Theoretically, it is interesting to know what types of nodes exist. But practitioners are concerned about a different question: how to create a transport hub for the unhindered movement of flows of cars or people. Such "nodes" can be seen on the topological map of surface and underground transport in Berlin.

There are even patents for knots. There is, for example, an American patent based on a special knot - a Möbius strip. The German mathematician August Ferdinand Möbius (1790-1868) twisted a flat ribbon once at an angle of 180° and glued both ends together. This tape is amazing. If we, having touched one of its sides with our finger (we note which), we slide it along the surface, we will find that this tape has only one surface (a tape not twisted in this way, of course, has two surfaces). The patent is based on this property. When using a drive belt (said in the patent description), its inner side, running over the driving and driven wheels, wears out over time and becomes unusable. When using a Möbius strip, the difference between the inner and outer surface essentially disappears and belt wear is correspondingly greatly reduced. In fact, it was patented.

A self-untying knot often used by magicians. If you pull on the "desired" end, the knot will unravel

If we make the Möbius strip transparent and put some icon on it, say the letter N, then it will be found that the opposite figures correlate like an image and its mirror image. This is quite curious, considering that the "straight" and "opposite" letters are on the same side of the tape! After all, the tape generally has only one surface.

When constructing complex intersections, it is important to know one property of nodes, which we will derive with the help of an experiment. Draw any transport hub. It can be confusing and wrong. Mark only each intersection with a letter, of course, in each case different. Now move your pencil or finger across your drawing in the opposite direction from where you drew. And every time you pass an intersection, write down the corresponding letter. To make the result (which we are trying to find) clearer, write the letters in two rows: either from left to right, or from top to bottom. It is only important that you alternate intersections (depending on whether the street passes above or below the other). And it does not matter how you took the first intersection - upper or lower. When the tablet is ready and you have checked it properly, you will find that each letter denoting an intersection occurs once in each of the rows.

Imagine that you have to design a system of traffic lights to control the passage of vehicles. One row will have all the traffic lights turned on green, while all the traffic lights in the other row should be turned on red.

Amateur magicians use knowledge of knot theory for a neat "mind-reading experiment." You ask to draw a similar knot and mark it with letters (without peeping), and then you offer to go around the obstacle, naming the letters (which the magician writes down according to the already known pattern). At some point, two intersections "get confused". And the magician, "reading" thoughts, calls the letters he meets. It is easy to check that the mixed up letters will appear twice in the same row.

To conclude this section, one more question: what happens if the Möbius strip is cut lengthwise? In the case of a simple, not inverted ribbon, this is clear: two new ribbons will be obtained, which will be twice as narrow as the first. What will happen to the Möbius strip, which we previously twisted before gluing its ends together, is hard to imagine! If after one turn one side has already “disappeared”, then in this case you can expect anything. Let's put the question a little differently: what happens if the owner of a patented belt drive cuts it lengthwise in order to save two belt drives? Experience tells us that two new tapes will not work. A closed tape will appear, twice as long. Although it is intertwined, it, like any normal ribbon, again has two sides.

MILK TRANSPORT AND BATHROOM FLOOR

Please turn back a few pages and take another look at the five Platonic solids. Only these five bodies (let's repeat this again) can be built from the same regular flat figures - faces.

The tetrahedron is familiar to us from everyday life. We buy dairy products in tetrahedral bags. Some time ago, the question was discussed why a tetrahedron, and not a hexahedron, that is, a cube, is used for these purposes. After all, the cube has the smallest (after the ball) surface in relation to the volume. Therefore, with such packaging for the same volume of milk, less packaging material would be needed than with packaging in tetrahedrons. However, if we look at the developments of both bodies, we will see that tetrahedra can be built from a continuous moving ribbon. But cubes from a simple tape will not work. Two squares will always stick out, so there will always be much more scraps than when gluing tetrahedron packages.

This small example allows you to analyze a common error. Often, in the search for the optimal solution, we forget to determine exactly what exactly should be optimized. A Low German proverb says: "What suits an owl is not good for a nightingale." In a modern way, it sounds something like this: “If you create optimal conditions for nightingales, what will owls have to do!” (And vice versa!)

In our packing problem, many questions can be asked, depending on what exactly should be optimal:

1. What gives the least amount of packaging for the same amount of content? (Ball, cube)

2. What is the easiest body to get from a flat sheet by simple folding? (Five Platonic solids, that is, not a ball!)

3. When assembled, which body has the shortest connecting strip that can be glued, welded, or connected in some other way? (Tetrahedron.)

4. When cutting which body does the least trimming result? (Tetrahedron.)

5. What bodies can be folded the most tightly, without gaps? (Cube, tetrahedron.)

6. Which body is least likely to “mix up” faces if it must lie on a certain side up (say, so that the marking is visible)? (A tetrahedron has the fewest faces.)

From asking these six questions, it's easy to see how carefully we need to specify what we're trying to optimize.

If we are faced with the task of developing a form of packaging for cargo intended for shipment by air, points 1 (small packaging format) and 5 (tight packing without gaps) will be the determining optimization criteria, since each gram costs extra money in air transport. But when choosing containers for transporting milk, point 3 (the shortest length of the gluing line) plays the main role, and even more important - point 4 (minimum waste). Here are added the advantages of points 5 (packing density) and 6 (the least chance of stacking packages on the wrong side).

If you go around this "node" along the arrow, then the letters will appear once in the "indirect" row and once - in the direct

Futurologists are already facing a problem today: will we buy milk in tetrahedrons in 2000 or only in powder, or maybe we will have to mess with milk cans again?

However, in this book we are primarily interested in questions that are closer to the topic.

Indeed, it is surprising that a polyhedron can also be built from pentagons. And why is it impossible from hexagons? Moreover, a hexagon can be built from six triangles?

Obviously, the point here is not only in the original flat figure itself (triangle, square, pentagon), but also in how these surfaces, adjoining, are connected to each other. If the hexagons are laid out on the table, it becomes clear that they cover the plane without gaps. This is also true for triangles and squares. But it is impossible to fold a three-dimensional body from hexagons without deforming them. If you still try to make such a polyhedron of hexagons with light pressure, its faces will bend and the shape will approach spherical.

A special kind of ball structure is a soccer ball. Millions of people see this ball on the TV screen many times a week. Hundreds of thousands see him "in kind", at the stadium. Everyone knows that the tires of the ball are made up of white and black pieces. But, oddly enough, only a few can say with certainty what kind of polygons it is made of. Even football players hesitate when they remember whether it is from five or from hexagons. This is a typical example of our carelessness in everyday life.

Formerly, the leather tire was made from two-pointed slices, similar to those that are cut on an orange peel. Most modern balls have a tire made of curved polygons. It weighs about 300 g with a ball circumference of about 64 cm and is made up of 12 black and 20 white "fields". The edge of each polygon, regardless of the number of its corners, is 4.3 cm long. Around each black pentagon are six white hexagons.

As already mentioned, on the plane, a hexagon surrounded by six other hexagons forms a motif of a continuous pattern. A pentagon surrounded by five hexagons does not fill the entire plane without gaps. But if, with some effort, we connect such polygons made of leather, we get (with a very good approximation) a ball - our soccer ball. Spatially deformed hexagons are also used in construction in the construction of modern lightweight structures.

Thus, from undeformed flat figures of the same type and size, only five Platonic solids can be combined.

Great opportunities for combinations of flat figures open up when composing patterns from tiles (for example, on the floor in the bathroom). They endlessly repeat motifs from equilateral triangles, squares and hexagons. But with pentagonal tiles, the tiler could hardly do anything. They cannot be folded into a similar pattern.

The special properties of an equilateral or isosceles triangle (for a square consists of two isosceles, and a hexagon of six equilateral triangles) are associated with the sum of its angles, which is 180 °. The sum of the angles of any n-gon is (n - 2) 180°. For a pentagon it will be (5-2) 180° = 540°. Dividing 540 by 5, we get 108° for each angle. At the points where all tiles converge, the sum of all angles must be 360°. But from angles equal to 108 °, it is impossible to make a total angle of 360 °!

We have already said that a tile pattern can only be made if you take regular triangles, squares and hexagons. However, this is true only when side to side and corner to corner are applied. But these three kinds of polygons will show differences as soon as we choose a different design motif for our floor. Squares and equilateral triangles will fill the entire plane even if they do not adjoin corner to corner. In the motif laid out with hexagons, gaps are formed between adjoining corners and sides. But these gaps themselves contribute to the creation of new delightful patterns. For hexagons, there are four motives for combining them into a single pattern with triangles and squares.

In addition, two more combinations are known in which only squares and triangles participate, and two in which, in addition, octagon and dodecagons are also used. Many mathematicians were fond of creating "patterns for tiles".

So, it is known that Johannes Kepler was engaged in drawing up a pattern of hexagons surrounded by triangles. It is curious that this pattern (and only it) can have a mirror image. The rest of the patterns in the mirror do not change. Only the Kepler pattern is flipped.

Taking any -polygons and not being limited by special rules when connecting them, we can come up with a great variety of mosaic patterns. Russian crystallographer E. S. Fedorov in 1891 proved that 17 different symmetry groups are distinguished in this case. In practice, these groups were already known to the Arabs and were used by them in the mosaics of the Alhambra in Spain.

The human eye tends to break up patterns further and further, especially if they are contrasting in color, like a checkerboard, for example. Let's start with a "chessboard", consisting of only two rows of two cells. (Instead of a checkerboard, you can use four square tiles on the floor or wall.)

How can you cut a 2X2 pattern in half? To answer this question, of course, is not difficult. Only one line passing in the middle either from left to right or from top to bottom and separating two cells (left or top).

A board consisting of 3x3 cells cannot be divided in half (without re-slicing the cells). In some games, however, playing fields 3X3, 5X5, etc. are used, excluding the middle i so that when the playing field is divided in half, an integer number of cells is obtained. But here we will not consider such already, and from those that are made up of a whole number of cells, the head can go round.

How many possibilities are there to bisect a pattern made up of 4 x 4 cells without crossing them? In this case, we will neglect the difference between top - bottom and left - right. (Such solutions can be translated into each other by a simple turn.) Anyone who properly tinkers with such a division will find, at the very least, 6 ways.

And if you try to divide the field of 6x6 cells? English puzzle maker Henry E. Dudeney found 255 ways to divide such a field. For a chessboard with 64 cells (8X8), the computer calculated 92,263 division options!

There are many similar problems that chess players and mathematicians struggle with. Problems of this kind remain favorite: how many queens (or bishops, or rooks) can be placed on one board so that they do not threaten each other? (For those who do not play chess, it should be noted that the queen has the right to move in all directions, including diagonals, as far as she likes.) Chess lovers have determined that there can be 8 queens on the board.

Here the next question arises: how many options are there for their arrangement? In 1850, Franz Nauk published an answer in the Leipzig "Illustrated Gazette": there are 12 such basic positions.

Since we've talked a lot about mirror planes, hopefully you'll draw a plane of symmetry across the chessboard from top to bottom without hesitation. This will be the first solution.

You can draw the next plane of mirror reflection from left to right, two more planes will pass diagonally. Thus, we have found four more solutions. Now let's rotate the field by 180° and again draw two diagonal mirror reflection planes and one from top to bottom. But here we can no longer draw a plane of symmetry from left to right: it will only give us the same picture that we have already seen.

Thus, by simple mirroring and rotation, we have added seven more options to the main position of the figures. With one single exception, this operation is possible for all other basic provisions that Science has found. In the exceptional case mentioned above, there are only three reflections. In total, queens can be simultaneously placed on the chessboard, without threatening each other, in 92 different positions.

This example teaches us how to benefit from the presence of symmetry. Of course, first it was necessary to establish that only 8 queens can be on the ole. Then it was necessary to develop 12 basic starting positions, which, of course, was not easy. But the remaining 80 variants could be found without being a chess expert. It was enough to know how the mirror works. On the other hand, it must be admitted that there are certainly many outstanding chess players who have never heard of planes of symmetry.

ON THE QUESTION OF DEFINITIONS

They say that every problem can be considered from three points of view: from mine, from yours, and from the point of view of facts.

Undoubtedly, there is something in this aphorism. The glass can be half empty or half full. You can have as much as 5 rubles in your pocket or as little as 5 rubles! Passengers are experiencing a strong storm, and the battered captain at the same time feels only a fresh breeze.

Let's define what a chessboard is. We can say that these are 64 cells, located in 8 longitudinal rows of 8 cells each, so that in general, all together they form a square. But you can put it differently: this is a square divided into 64 equal square cells. (In both cases, we should also talk about black and white fields, but since this circumstance is not essential for our purposes, we will omit this part of the definition.) In the first case, we form a large square from small ones, in the second, we divide a large one into small ones.

For the sake of curiosity, let's ask, how many parts can a square be divided into so that small but identical squares appear? Obviously, the square is divisible into at least 4 smaller squares. It is impossible to divide it into 2 or 3 squares. At the next division, each of the four small squares will be divided into 4 even smaller ones, that is, there will be 16 squares in total. We learned the course of division. Each time we get the result by multiplying by 4. Accordingly, the next time we divide 16 squares, we get 64, that is, a chessboard. There are only two flat figures that can be divided into two equal parts, and these parts will be exact reduced reproductions of large figures. Since we are accustomed to halving everything that occurs around us, one has only to be surprised that in only two cases can we comply with the condition formulated above. These are such figures: a right-angled isosceles triangle and a parallelogram with an aspect ratio of 1: √ 2.

Such a parallelogram in one particular case - in the form of a rectangle - plays an essential role in art and technology. A rectangle whose long side is √2 times larger than its short side (that is, 1.4142 times) is perceived by us as commensurate. It is this or a format close to it that artists prefer.

In photography, 7X10 formats (formerly 6x9) and 13X18 are widely used. If you calculate the aspect ratio, it turns out 10:7 ≈ 1.43, and 18:13 ≈ 1.38, that is, numbers close to √ 2 = 1.4142.

More precisely adhere to the ratio 1: √ 2 in the technique. It is based on the paper size. So, with the AO format (841 x 1189 mm), the aspect ratio is 1.413 ≈ √ 2. If you bend the sheet in half, on the larger side, you get the A1 format (841X1189 / 2, that is, 841X594 mm), where 841:594 = 1.415. Then the big side is folded in half again. It turns out the A3 format. With the next folding, we get the well-known A4 format, in which 291:210 \u003d 1.414. This division goes further up to the A8 format (74:52).

Those who deal with paper know that there are two other rows - for dust jackets and other purposes. Row B starts at 1414:1000 = 1.414 and row C starts at 1297:917 = 1.414...

The book you are reading (and hopefully not without interest) has a format of 260x200 mm, and 260:200 = 1.3.

Of course, you noticed that the paper format here is not indicated exactly as it is customary: not through the product of the parties, but through their ratio, but we allowed ourselves this for greater clarity.

We could say that the calculation of the paper size that meets the standard is made by re-dividing the sheet with an aspect ratio of 1: √ 2, starting from the format 917X1297 mm. But another definition would be more correct: the standard paper calculation is performed by proportionally enlarging the sheet with an aspect ratio of 1:√2, sequentially starting from the 52X74 mm format. In both cases, one should make a reservation that in division (or multiplication) each time a side with a relative length of √ 2 is taken.

Recall that a rectangle is only a special case of a parallelogram, and that a parallelogram with an aspect ratio of 1:√2, as well as a right isosceles triangle, can be divided into two smaller copies.

A parallelogram with one side equal to √3 can be divided into 3 reduced similar parts. In general form: a parallelogram with an aspect ratio of 1:√ n can be divided into n identical similar parts.

There are many more figures that have a variety of separation options. We will consider another motif, which was sometimes laid out on ancient tiled floors in the corners. These are trapeziums, which the mirror reflection turns into an integral motif of the pattern. Here again there is a "reflection". This means that in such patterns combinations of flat figures are permissible that cannot be combined with each other by rotation or rotation, that is, "left" and "right".

How to lay bars or bricks so that the structure does not have through "seams"

The figure shown here brings us to divisions without discontinuity. If, when the paper size was reduced, the surface of the figure was crossed by a gap (fold or line), then in our main pattern there are lines that do not continue, but rest against other lines. Sometimes it is especially desirable to completely avoid division with gaps. Let's say we would like the wall of a brick house to not have a seam that crosses the entire wall from top to bottom. Instructions for welding drums of boilers and oil pipes of large diameter prohibit the contact of two longitudinal and two transverse seams. Only one longitudinal seam in one direction can abut against each transverse or circular seam. The longitudinal seam of the other direction must certainly be shifted to the side. Due to this, tears in the longitudinal seam will only extend to the next transverse seam.

Now you probably already guessed what task you are offered: assemble the surface depicted here from standard parts (bricks, parquet or sheets of tin), without violating its continuity.

LEGENDS OF MINERS

In the old days, miners were purely practical people. They did not bother themselves with the names of all kinds of rocks that they met in the adit, but simply divided these rocks and minerals into useful and useless, unnecessary. The necessary ones were extracted from the bowels, copper, lead, silver and other metals were smelted from them, and the unnecessary ones were dumped into dumps.

For useful (in their opinion) minerals, they looked for descriptive and memorable names. You may never see a spear-shaped pyrite, but without much difficulty imagine it by its name. It is not more difficult to distinguish red iron ore from brown iron ore by name.

For useless stones (as already mentioned - in their opinion), miners often found names in legends and legends. So, for example, the name of the ore cobalt shine occurred. Cobalt ores are similar to silver ores and were sometimes mistaken for them when mined. When silver could not be smelted from such ore, it was believed that it was bewitched by mountain spirits - kobolds.

When mineralogy turned into a science, a great variety of rocks and minerals were discovered. And at the same time, more and more difficulties arose with the invention of names for them. New minerals were often named after the place of discovery (ilmenite - in the Ilmensky mountains) or in honor of a famous person (goethite - in honor of Goethe) or they gave him a Greek or Latin name.

Museums were replenished with grandiose collections of stones, which were already boundless. Chemical analyzes did not help much either, because many substances of the same composition sometimes form crystals of completely different shapes. Suffice it to recall at least snowflakes.

In 1850, the French physicist Auguste Bravais (1811-1863) put forward a geometric principle for the classification of crystals based on their internal structure / According to Bravais, the smallest, endlessly repeating pattern motif is the defining, decisive feature for the classification of crystalline substances. Brave imagined a tiny elementary particle of a crystal at the basis of a crystalline substance. Today, from the school bench, we know that the world consists of the smallest particles - atoms and molecules. But Bravais operated in his ideas with a tiny "brick" of a crystal and investigated what angles between the edges could be and in what proportions of its sides could be between themselves ( For greater clarity, the author simplifies the history of the derivation of Bravais lattices. Bravais's predecessor, the French crystallographer R. J. Hayuy (1743-1822), really imagined crystals to be made up of elementary "bricks". O. Brave replaced these "bricks" with their centers of gravity and thus moved from the "brickwork" of Gajuy to a spatial lattice. - Approx. ed).

In a cube, three edges are always at an angle of 90° to each other. All sides are of equal length. Bricks also have 90° angles. But its sides are of different lengths. In snowflakes, on the contrary, we will not find an angle of 90 °, but only 60 or 120 °.

Brave found that there are 7 combinations of cells with the same or different sides (axes) and angles. For angles, he accepted only two options: equal to 90° and not equal to 90°. Only one angle in his entire system, as an exception, has 120°. In the worst case, all three axes and all angles of the cell are different in magnitude, while it does not have angles of either 90 or 120 °. Everything in it is slanted and crooked, and, one might think, in the world of crystals this should not be the place. Meanwhile, they include, for example, copper sulfate (copper sulfate), whose blue crystals are usually liked by everyone.

In some of these 7 spatial grids, the elementary "bricks" can be packed in different ways. For us, who know today about the structure of the atom, this is not difficult to imagine and demonstrate with the help of ping-pong balls. But 125 years ago, Bravais's brilliant idea was innovative and opened up new paths in science. It is very likely that Bravais also proceeded from tile patterns or chessboard motifs.

If we divide the square fields by diagonals, then a new pattern arises from the squares at the corners. In three-dimensional space, this corresponds to a cube decomposed into six pyramids. Each such pyramid is half an octahedron.

Those who have ever grown salt crystals know that salt can crystallize in cubes, or maybe in octahedrons. In other words, experimental observations will be consistent with theoretical considerations.

After trying possible packaging options for all seven axle systems, Bravais came up with 14 lattices. We present them here in our modern atomistic image.

If you take a closer look at the Bravais lattices and try to mentally build crystals out of them, you will probably see how you can draw planes and axes of symmetry in them. These possibilities will immediately expand if we form new faces in one of the elementary cells. Let's take a cube (of course, mentally!), put it on a corner and cut off (still mentally) all the corners, then it will form completely new triangular faces. And from the square faces, octagons will arise: thereby new symmetry motifs will appear.

Analysis of the symmetry elements in each of the axial systems of crystal lattices leads to the emergence of 32 symmetry classes. The whole variety of minerals in nature is subdivided on the basis of 32 symmetry classes. Armed with this knowledge, let's think about the classification of Plato's five solids. The fact that the cube, with its three equal axes and three right angles, belongs to the cubic axial system (syngony) does not need proof. Within a more detailed subdivision, it belongs to the pentagon-tetrahedral symmetry class ( The cubic system includes 5 out of 32 classes of crystallographic symmetry. These include 5 varieties of the cube, differing in symmetry. The most symmetrical cube has 9 planes of symmetry, 3 quadruple, 4 triple and 6 double axes of symmetry. The least symmetrical cube, which is discussed in the text, has only three double and four triple axes of symmetry. - Approx. ed). We will not give the names of other classes here because of their complexity. However, note the term "tetrahedral", as the tetrahedron is one of the Platonic solids.

And if you have a good memory, you will remember the pentagondode-kahedron, which is also included in this symmetry class. The picture clearly shows how a tetrahedron can be formed from a cube. The rest of the Platonic solids also belong to the cubic system. The ancient Greeks, one must think, would have been terribly upset if they had known that such a prosaic mineral as sulfur pyrite had the same symmetry as their "perfect" bodies.

Man is able to see through light. Light quanta - photons have the properties of both waves and particles. Light sources are divided into primary and secondary. In the primary - such as the Sun, lamps, fire, electric discharge - photons are born as a result of chemical, nuclear or thermonuclear reactions. Any atom serves as a secondary source of light: having absorbed a photon, it goes into an excited state and sooner or later returns to the main one, emitting a new photon. When a beam of light hits an opaque object, all of the photons that make up the beam are absorbed by the atoms on the surface of the object. Excited atoms almost immediately return the absorbed energy in the form of secondary photons, which are evenly radiated in all directions. If the surface is rough, then the atoms on it are arranged randomly, the wave properties of light do not appear, and the total radiation intensity is equal to the algebraic sum of the radiation intensity of each re-emitting atom. In this case, regardless of the viewing angle, we see the same light flux reflected from the surface - such a reflection is called diffuse. Otherwise, light is reflected from a smooth surface, such as a mirror, polished metal, glass. In this case, the atoms re-emitting light are ordered relative to each other, the light exhibits wave properties, and the intensities of the secondary waves depend on the phase differences of neighboring secondary light sources. As a result, the secondary waves compensate each other in all directions, except for one single one, which is determined according to a well-known law - the angle of incidence is equal to the angle of reflection. Photons seem to rebound elastically from the mirror, so their trajectories go from objects that are, as it were, behind it - they are what a person sees when looking into the mirror. True, the looking-glass world is different from ours: the texts are read from right to left, the clock hands turn in the opposite direction, and if you raise your left hand, our double in the mirror will raise his right, and the rings are on the wrong hand ... Unlike the movie screen, where All viewers see the same image, reflections in the mirror are different for everyone. For example, the girl in the picture does not see herself in the mirror at all, but the photographer (since he sees her reflection). To see yourself, you need to sit in front of the mirror. Then the photons coming from the face in the direction of gaze fall on the mirror almost at a right angle and come back. When they reach your eyes, you see your image on the other side of the glass. Closer to the edge of the mirror, the eyes catch photons reflected by it at a certain angle. This means that they also came at an angle, that is, from objects located on either side of you. This allows you to see yourself in the mirror along with the surroundings. But less light is always reflected from the mirror than it falls, for two reasons: there are no perfectly smooth surfaces, and the light always heats the mirror a little. Of the widely used materials, polished silver reflects light best (more than 95%). Mirrors were made from it in ancient times. But in the open air, silver tarnishes due to oxidation, and the polish is damaged. In addition, a metal mirror is expensive and heavy. Now a thin layer of metal is applied to the back of the glass, protecting it from damage with several layers of paint, and aluminum is often used instead of silver to save money. Its reflectance is about 90%, and the difference is imperceptible to the eye.