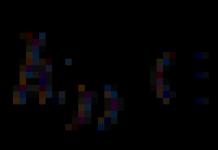En el caso de flexión transversal en las secciones de la viga, no solo surge un momento de flexión, sino también una fuerza transversal. En consecuencia, en este caso, no solo surgen tensiones normales, sino también tangenciales en las secciones transversales de la viga.
Dado que las tensiones tangenciales generalmente se distribuyen de manera desigual sobre la sección transversal, estrictamente hablando, las secciones transversales de la viga no permanecen planas durante la flexión transversal. Sin embargo, en (donde h- altura de la sección transversal, yo es la longitud de la viga) resulta que estas distorsiones no afectan notablemente el trabajo de la viga en flexión. En este caso, la hipótesis de secciones planas también es aceptable con suficiente precisión en el caso de flexión pura. Por tanto, se utiliza la misma fórmula (6.4) para calcular las tensiones normales s.
Considere la derivación de fórmulas de cálculo para esfuerzos cortantes. Destaquemos de la barra que experimenta flexión transversal un elemento con una longitud dx(Figura 6.6 A).

| A |
| b |
| V |
| GRAMO |
| A * |

Sección horizontal longitudinal dibujada a distancia z desde el eje neutral, dividimos el elemento en dos partes (Fig. 6.6 V) y considere el equilibrio de la parte superior, que tiene una base de ancho b. Al mismo tiempo, teniendo en cuenta la ley de emparejamiento de tensiones tangenciales, obtenemos que las tensiones tangenciales en la sección transversal son iguales a las tensiones tangenciales que surgen en las secciones longitudinales (Fig. 6.6 b). Teniendo en cuenta esta circunstancia y partiendo de la suposición de que los esfuerzos cortantes sobre el área b× dx están distribuidas uniformemente, usando la condición åx = 0, obtenemos:
norte * - norte * - dN* + t × b× dx = 0 ,
 . (6.5)
. (6.5)
Dónde norte* - resultante de fuerzas normales s× dA en la sección transversal izquierda
elemento dx dentro de la plaza A* (Figura 6.6 GRAMO):
 . (6.6)
. (6.6)
Teniendo en cuenta (6.4), la última expresión se puede representar como
 , (6.7)
, (6.7)
Dónde  - momento estático de la parte de la sección transversal situada por encima de la coordenada y(en la Fig. 6.6b esta área está sombreada).
- momento estático de la parte de la sección transversal situada por encima de la coordenada y(en la Fig. 6.6b esta área está sombreada).
Por lo tanto, (6.7) se puede reescribir como  , dónde
, dónde
 . (6.8)
. (6.8)
Como resultado de la consideración conjunta de (6.7) y (6.8), obtenemos
 ,
,
o finalmente
 . (6.9)
. (6.9)
La fórmula (6.9) lleva el nombre del científico ruso D.I. Zhuravski.
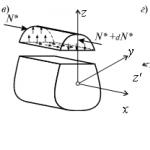
Para estudiar el estado de tensión en un punto arbitrario de una viga que experimenta flexión transversal, seleccionamos un prisma elemental de la composición de la viga alrededor del punto bajo estudio (Fig. 6.6 GRAMO), de modo que la plataforma vertical es parte de la sección transversal de la viga, y la plataforma inclinada forma un ángulo arbitrario con respecto al horizonte. Aceptamos que el elemento seleccionado tiene las siguientes dimensiones a lo largo de los ejes de coordenadas: a lo largo del eje longitudinal - dx, es decir. a lo largo del eje X; a lo largo del eje vertical - dz, es decir. a lo largo del eje z; a lo largo del eje y- igual al ancho de la viga.
Dado que el área vertical del elemento seleccionado pertenece a la sección transversal de la viga que experimenta flexión transversal, las tensiones normales s en este sitio están determinados por la fórmula (6.4), y los esfuerzos cortantes t- según la fórmula D.I. Zhuravsky (6.9). Teniendo en cuenta la ley de emparejamiento de esfuerzos cortantes, es fácil establecer que los esfuerzos cortantes en una plataforma horizontal también son iguales t. Las tensiones normales en este sitio son iguales a cero, según la hipótesis de la teoría de la flexión ya conocida por nosotros de que las capas longitudinales no ejercen presión entre sí.
Denotemos los valores de los esfuerzos normales y cortantes en el área inclinada a través de es un Y ejército de reserva, respectivamente. Tomando el área de la pendiente dA, para plataformas verticales y horizontales tendremos dA pecado y dA porque a respectivamente.
Composición de las ecuaciones de equilibrio para un prisma de corte elemental (Fig. 6.6 GRAMO), obtenemos:

 ,
,
de donde tendremos:
Por lo tanto, las expresiones finales para esfuerzos sobre una plataforma inclinada toman la forma:

Determinemos la orientación del sitio, es decir. valor a = a 0 , en el cual el voltaje s a toma un valor extremo. De acuerdo con la regla para determinar los extremos de las funciones del análisis matemático, tomamos la derivada de la función s a de a y la igualamos a cero:
 .
.
Asumiendo un = un 0, obtenemos:  .
.
De donde finalmente tendremos:  .
.
De acuerdo con la última expresión, los esfuerzos extremos surgen en dos áreas perpendiculares entre sí, llamadas principal, y las propias tensiones - tensiones principales.
Comparando las expresiones ta y  , tenemos:
, tenemos:  , de donde se sigue que las tensiones tangenciales en las áreas principales son siempre iguales a cero.
, de donde se sigue que las tensiones tangenciales en las áreas principales son siempre iguales a cero.
En conclusión, teniendo en cuenta las conocidas identidades trigonométricas:

y fórmulas  , determinamos las tensiones principales, expresadas en términos de s y t.
, determinamos las tensiones principales, expresadas en términos de s y t.
Hemos visto que en la flexión pura sólo surgen esfuerzos normales en las secciones transversales de la barra. Los esfuerzos internos correspondientes se reducen a un momento de flexión en la sección. En el caso de la flexión transversal en la sección de la varilla, no solo surge un momento de flexión, sino también una fuerza transversal, que es la resultante de fuerzas elementales distribuidas que se encuentran en el plano de la sección (Fig. 4.23). En consecuencia, en este caso, no solo surgen esfuerzos normales, sino también esfuerzos cortantes en las secciones transversales.

La aparición de tensiones tangenciales va acompañada de la aparición de deformaciones angulares. Por lo tanto, además de los desplazamientos básicos inherentes a la flexión pura, cada área elemental de la sección recibe unos desplazamientos angulares adicionales por cortante. Los esfuerzos cortantes se distribuyen de manera desigual sobre la sección, por lo que los desplazamientos angulares también se distribuirán de manera desigual. Esto significa que en caso de flexión transversal, a diferencia de la izpb a pura, las secciones transversales no permanecen planas. En la fig. 4.24 muestra una imagen típica de la curvatura de las secciones transversales.


Sin embargo, la distorsión del plano de las secciones transversales no afecta notablemente el valor de las tensiones normales. En particular, si la fuerza transversal no cambia a lo largo de la barra, las fórmulas (4.6) y (4.8), derivadas para el caso de flexión pura, darán resultados completamente precisos en el caso de flexión transversal. De hecho, cuando la curvatura de todas las secciones se produce de la misma manera (Fig. 4.25). Por lo tanto, con la rotación mutua de dos secciones adyacentes, el alargamiento de la fibra longitudinal AB será el mismo, independientemente de que la sección permanezca plana o no.
Con una fuerza transversal que varía a lo largo del eje de la barra, las fórmulas de flexión pura dan algún error para a. Mediante un simple análisis, se puede demostrar que este error es del orden de magnitud en comparación con la unidad, donde es el tamaño de la sección transversal en el plano de flexión; - longitud de la varilla. De acuerdo con la definición dada en el § B2, un rasgo característico de una barra es que las dimensiones de su sección transversal son mucho menores que su longitud. En consecuencia, la relación es relativamente pequeña y el error especificado resulta ser correspondientemente pequeño.
Todo lo anterior da razón para aceptar la hipótesis de las secciones planas. Supondremos además que el conjunto de puntos que forman el plano de la sección transversal antes de la flexión también forma un plano rotado en el espacio después de la flexión. Esta suposición es aceptable en la medida en que las deformaciones angulares 7 en la sección pueden considerarse significativamente menores que los desplazamientos angulares debidos al cambio de curvatura.
Una característica de la flexión transversal es también la presencia de tensiones normales que surgen en las secciones longitudinales de la viga, es decir. tensiones entre capas. Estas tensiones surgen solo con una fuerza transversal variable y son muy pequeñas.
Así, dentro de los supuestos indicados, las fórmulas (4.6) y (4.8), derivadas para determinar las tensiones normales, son aplicables no sólo a la flexión pura, sino también a la flexión transversal. Igualmente aplicable es la fórmula (4.5), que da la dependencia de la curvatura de la barra en el momento de flexión.
Ahora determinemos aproximadamente las tensiones tangenciales en la flexión transversal. La forma más fácil de calcular estos esfuerzos es a través de los esfuerzos cortantes apareados que surgen en las secciones longitudinales de la varilla. Seleccionemos un elemento de longitud de la viga (Fig. 4.26, a). En caso de flexión transversal, los momentos que surgen en las secciones izquierda y derecha del elemento no son los mismos y difieren en la sección horizontal longitudinal dibujada a una distancia y de la capa neutra (Fig. 4.26, b), dividimos el elemento en dos partes y considere las condiciones de equilibrio de la parte superior. La resultante de las fuerzas normales en la sección izquierda dentro del área sombreada es, obviamente,

o, según la fórmula (4.6),


donde, a diferencia de y, denota la ordenada actual del sitio (ver Fig. 4.26, b). La integral resultante es el momento estático con respecto al eje x de la parte del área ubicada por encima de la sección longitudinal (por encima del nivel). Denotemos este momento estático por Entonces

En la sección derecha, la fuerza normal será diferente:

La diferencia entre estas fuerzas

debe estar equilibrado por fuerzas tangenciales que surgen en la sección longitudinal del elemento (ver Fig. 4.26, b y c).
Como primera aproximación, suponemos que los esfuerzos cortantes se distribuyen uniformemente sobre el ancho de la sección. Entonces
![]()
La fórmula resultante se llama fórmula de Zhuravsky, en honor al científico ruso del siglo pasado, quien fue el primero en realizar un estudio general de los esfuerzos cortantes en la flexión transversal.
La expresión (4.12) permite calcular los esfuerzos cortantes que surgen en las secciones longitudinales de la barra. Los esfuerzos formados en las secciones transversales de la varilla son iguales a ellos, como un par. La dependencia de y en la sección se determina a través del momento estático 5. Al acercarse al borde superior de la sección, el área de su parte sombreada (ver Fig. 4.26, b) se reduce a cero. Aquí, por lo tanto, al acercarse al borde inferior, la parte sombreada cubre toda la sección. Dado que el eje es central, entonces aquí también Por lo tanto, los esfuerzos cortantes, como se deduce de la fórmula (4.12), en los puntos superior e inferior de la sección son iguales a cero.

Para una barra rectangular con lados y (Fig. 4.27, a) tenemos
Por eso,

y el diagrama de tensiones tangenciales a lo largo de la altura de la sección está representado por una parábola cuadrada. El mayor estrés se produce en
![]()
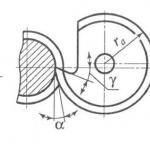
Para una barra circular (Fig. 4.27, b), mediante una simple operación de integración, puede encontrar

Además,
![]()
![]()
Para una barra que tiene una sección en forma de triángulo con una base c y una altura (Fig. 4.27, c),

La tensión máxima se produce a una distancia del eje neutro:
![]()
Los dos últimos ejemplos demuestran claramente la naturaleza aproximada de las operaciones realizadas. Esto se puede ver por el hecho de que en la sección transversal, los esfuerzos cortantes tienen componentes no solo a lo largo del eje y, sino también a lo largo del eje x. De hecho, supongamos, como se hizo anteriormente, que para los puntos A ubicados cerca del contorno de la sección (figura 4.28), el esfuerzo cortante está dirigido a lo largo del eje y. Descompongamos el vector en dos componentes: a lo largo de la normal al contorno y a lo largo de la tangente.De acuerdo con las condiciones de carga, la superficie exterior de la barra está libre de fuerzas tangenciales. Por lo tanto, no hay pares de voltaje. Por lo tanto, mientras que el esfuerzo cortante total cerca del contorno se dirige tangencialmente al contorno, la suposición de que se dirige a lo largo del eje y resulta ser incorrecta. Así, se detecta la presencia de componentes a lo largo del eje x. Para determinar estos componentes, se debe recurrir a métodos más complejos que


revisado anteriormente. Usando los métodos de la teoría de la elasticidad, se puede demostrar que, en la mayoría de los casos, los componentes a lo largo del eje x juegan un papel significativamente menor que a lo largo del eje y.
De los ejemplos considerados anteriormente, podemos sacar una conclusión general de que la zona de esfuerzos cortantes máximos se encuentra aproximadamente en la parte media de la altura de la sección, y para secciones sin paredes delgadas tiene un valor del orden
Es posible comparar los valores absolutos de los esfuerzos máximos normales y máximos de corte que surgen en las secciones transversales de la barra. Por ejemplo, para una consola rectangular (Fig. 4.29) tenemos

Esto significa que los esfuerzos cortantes máximos en la sección transversal están relacionados con los esfuerzos normales máximos aproximadamente como la altura de la sección está relacionada con la longitud de la varilla, es decir los esfuerzos cortantes son significativamente menores de lo normal. La estimación especificada, con algunas excepciones, se conserva para todas las barras que no sean de paredes delgadas. En cuanto a las varillas de pared delgada, este es un tema especial.
Debido a la pequeñez de τmax, el cálculo de la resistencia en flexión transversal se realiza solo para tensiones normales, como en flexión pura. No se tienen en cuenta los esfuerzos cortantes. Esto es tanto más natural cuanto que en los puntos del tramo más alejados de la línea neutra, es decir, en los más peligrosos, los esfuerzos cortantes en la sección transversal son cero.
Considerando el lado cualitativo del fenómeno, se debe tener en cuenta que los esfuerzos cortantes en las secciones transversales y sus esfuerzos apareados en las secciones longitudinales, a pesar de su pequeño tamaño, pueden en algunos casos afectar significativamente la evaluación de la resistencia de la barra. Por ejemplo, al doblar transversalmente una viga de madera corta, no es posible la destrucción a lo largo de la sección transversal en el empotramiento, sino el corte a lo largo del plano longitudinal cerca de la capa neutra, es decir donde los esfuerzos cortantes son máximos (figura 4.30).

Los esfuerzos cortantes en secciones longitudinales son una expresión de la conexión existente entre las capas de la barra durante la flexión transversal. Si esta conexión se rompe en algunas capas, cambia la naturaleza de la flexión de la varilla. Por ejemplo, en una varilla formada por láminas (Fig. 4.31, a), cada lámina se dobla de forma independiente en ausencia de fuerzas de fricción. La fuerza externa sobre la lámina es igual a y el mayor esfuerzo normal en la sección transversal de la lámina es igual a
En el caso de flexión transversal en las secciones de la viga, no solo se produce un momento de flexión, sino también una fuerza transversal. En consecuencia, en este caso, no solo surgen tensiones normales, sino también tangenciales en las secciones transversales de la viga.
Dado que las tensiones tangenciales generalmente se distribuyen de manera desigual sobre la sección transversal, estrictamente hablando, las secciones transversales de la viga no permanecen planas durante la flexión transversal. Sin embargo, en (donde h- altura de la sección transversal, yo- la longitud de la viga) resulta que estas distorsiones no afectan notablemente el trabajo de la viga en flexión. En este caso, la hipótesis de secciones planas también es aceptable con suficiente precisión en el caso de flexión pura. Por lo tanto, se utiliza la misma fórmula (5) para calcular las tensiones normales.
Considere la derivación de fórmulas de cálculo para esfuerzos cortantes. Destaquemos de una barra que experimenta flexión transversal un elemento con una longitud (Fig. 6.28, A).
Arroz. 6.28
Con una sección horizontal longitudinal dibujada a una distancia y del eje neutral, dividimos el elemento en dos partes (Fig. 6.28, V) y considere el equilibrio de la parte superior, que tiene una base de ancho b. Al mismo tiempo, teniendo en cuenta la ley de emparejamiento de tensiones tangenciales, obtenemos que las tensiones tangenciales en la sección transversal son iguales a las tensiones tangenciales que surgen en las secciones longitudinales (Fig. 6.28, b). Teniendo en cuenta esta circunstancia y partiendo del supuesto de que los esfuerzos cortantes se distribuyen uniformemente en el área, utilizando la condición , se obtiene:
donde es la resultante de las fuerzas normales en la sección transversal izquierda del elemento dentro del área sombreada:
Teniendo en cuenta (5), la última expresión se puede representar como
donde es el momento estático de la parte de la sección transversal ubicada sobre la coordenada y (en la Fig. 6.28, b esta área está sombreada). Por lo tanto, (15) se puede reescribir como
Como resultado de la consideración conjunta de (13) y (16), obtenemos
o finalmente
La fórmula resultante (17) lleva el nombre del científico ruso D.I. Zhuravski.
Condición de resistencia para esfuerzos cortantes:
donde es el valor máximo de la fuerza transversal en la sección; - Esfuerzo cortante admisible, suele ser igual a la mitad.
Para estudiar el estado de tensión en un punto arbitrario de una viga que experimenta flexión transversal, seleccionamos un prisma elemental de la composición de la viga alrededor del punto en estudio (Fig. 6.28, GRAMO), de modo que la plataforma vertical es parte de la sección transversal de la viga, y la plataforma inclinada forma un ángulo arbitrario con respecto al horizonte. Aceptamos que el elemento seleccionado tiene las siguientes dimensiones a lo largo de los ejes de coordenadas: a lo largo del eje longitudinal - dz, es decir. a lo largo del eje z; a lo largo del eje vertical - dy, es decir. a lo largo del eje en; a lo largo del eje X- igual al ancho de la viga.
Dado que el área vertical del elemento seleccionado pertenece a la sección transversal de la viga que experimenta flexión transversal, las tensiones normales en esta área están determinadas por la fórmula (5) y las tensiones cortantes están determinadas por el D.I. Zhuravsky (17). Teniendo en cuenta la ley de emparejamiento de esfuerzos cortantes, es fácil establecer que los esfuerzos cortantes en una plataforma horizontal también son iguales. Las tensiones normales en este sitio son iguales a cero, según la hipótesis de la teoría de la flexión ya conocida por nosotros de que las capas longitudinales no ejercen presión entre sí.
Denotemos los valores de las tensiones normales y tangenciales en el área inclinada a través de y , respectivamente. Tomando el área de la plataforma inclinada , para las plataformas vertical y horizontal tendremos y , respectivamente.
Composición de las ecuaciones de equilibrio para un prisma de corte elemental (Fig. 6.28, GRAMO), obtenemos:
de donde tendremos:
Por lo tanto, las expresiones finales para esfuerzos sobre una plataforma inclinada toman la forma:
Determinemos la orientación del sitio, es decir. el valor en el que el voltaje alcanza su valor extremo. De acuerdo con la regla para determinar los extremos de las funciones del análisis matemático, tomamos la derivada de la función y la igualamos a cero:
Suponiendo que obtenemos:
De donde finalmente tendremos:
De acuerdo con la última expresión, los esfuerzos extremos surgen en dos áreas perpendiculares entre sí, llamadas principal , y las propias tensiones - tensiones principales.
Comparando las expresiones y , tenemos:
de donde se sigue que las tensiones tangenciales en las áreas principales son siempre iguales a cero.
En conclusión, teniendo en cuenta las conocidas identidades trigonométricas:
y fórmulas,
determinamos las tensiones principales, expresando de a través de y:
Cortamos de la viga en la vecindad de un cierto punto un paralelepípedo elemental 1-2-3-4 (Fig. 45.7, a) cuyas caras laterales 1-2 y 3-4 están ubicadas en las secciones transversales de la viga, y las caras laterales 2-3 y 1-4 son capa neutra paralela. La longitud de la caja (en la dirección perpendicular al dibujo) es igual al ancho de la viga. Los esfuerzos que actúan sobre las caras del paralelepípedo se consideran en los § 7.7 y 8.7; se muestran en la fig. 45.7b. En las caras 1-2 y 3-4 actúan tensiones normales a y tangenciales, y en las caras 2-3 y 1-4 sólo actúan tensiones tangenciales. Las direcciones de estos voltajes, que se muestran en la fig. 45.7, b, corresponden al caso cuando el momento de flexión positivo y la fuerza transversal actúan en las secciones transversales de la sección de la viga en consideración.

Los valores de tensión están determinados por las fórmulas (17.7) y (28.7).
Las caras anterior y posterior del paralelepípedo elemental coinciden con las superficies laterales de la viga, libres de carga, y por tanto los esfuerzos sobre estas caras son nulos. En consecuencia, el paralelepípedo se encuentra en un estado de tensión plano.
En áreas inclinadas en diferentes ángulos a las caras laterales de un paralelepípedo elemental, actúan tensiones normales y tangenciales, cuyos valores pueden determinarse mediante las fórmulas (6.3) y (7.3). Hay dos áreas mutuamente perpendiculares a lo largo de las cuales los esfuerzos cortantes son iguales a cero. Estas áreas, como es sabido, se denominan áreas principales, y las tensiones normales que actúan en ellas se denominan tensiones principales (ver § 3.3). En áreas inclinadas en ángulos de 45° con respecto a las áreas principales, actúan esfuerzos cortantes extremos; estas áreas se denominan áreas de cizalla (ver § 4.3).
La determinación de los esfuerzos cortantes normales y extremos principales en el caso general de un estado tensional plano se realiza, como es sabido, según las fórmulas (12.3) y (15.3):

Sustituye en estas fórmulas los valores

Aquí, tensiones normales y tangenciales en el punto en consideración, que actúan en el sitio, coinciden con la sección transversal de la viga y están determinadas por las fórmulas (17.7) y (28.7).
De la fórmula (32.7) se puede ver que el voltaje otax es siempre positivo, a es siempre negativo. Por lo tanto, de acuerdo con la regla, según la cual se debe designar el voltaje otax y se debe designar la tensión. La tensión principal intermedia ocurre en las áreas principales paralelas al plano del dibujo (Fig. 45.7).
El ángulo de inclinación de las plataformas principales a las caras laterales de un paralelepípedo elemental se puede determinar por el método especificado en el § 3.3.
Los valores de los principales esfuerzos de corte normales y extremos y las posiciones de los sitios en los que actúan también se pueden determinar utilizando el círculo de Mohr (ver § 5.3).
Consideremos ahora con más detalle el estado de tensión en los puntos de la sección transversal rectangular de la viga. Suponga que el momento flector M y la fuerza transversal Q en esta sección son positivos.
En la sección transversal, en los puntos más alejados del eje neutro, los esfuerzos cortantes son cero y los esfuerzos normales a son iguales (en el punto a en la Fig. 46.7, a) y (en el punto a en la Fig. 46.7, a). Por tanto, para cada uno de estos puntos, una de las áreas principales coincide con la sección transversal de la viga, y las otras dos son perpendiculares a la sección transversal (las tensiones normales en ellas son iguales a cero). En estos puntos, existe un estado de tensión uniaxial.
En la fig. 46.7, pero se muestran paralelepípedos elementales, cuyas caras laterales son paralelas a las dos plataformas principales; la tercera plataforma principal es paralela al plano del dibujo. Los esfuerzos cortantes extremos en los puntos a a a están determinados por la fórmula
En la sección transversal en los puntos ubicados en el eje neutral (punto b en la Fig. 46.7, a), el esfuerzo normal o es cero y el esfuerzo cortante. En estos puntos, el estado tensional es de cortante puro con esfuerzos cortantes extremos
Las dos plataformas principales en cada uno de estos puntos están inclinadas en ángulos de ± 45 ° con respecto al eje de la viga (ver Fig. 46.7, a), y las tensiones principales en ellas.
La tercera plataforma principal es paralela al plano del dibujo; las tensiones en él son iguales a cero.
En la sección transversal en otros puntos, los esfuerzos a y son distintos de cero. A diferentes distancias del eje neutral, las relaciones entre los valores de a y son diferentes y, por lo tanto, los ángulos de inclinación de las plataformas principales con respecto al eje de la viga también son diferentes. En cada uno de estos puntos, las tensiones principales que no son iguales a cero tienen signos opuestos, es decir, el estado de tensión es tanto de tensión como de compresión en dos direcciones mutuamente perpendiculares.

Habiendo determinado los valores de las tensiones principales para varios puntos ubicados en la misma sección transversal de la viga a diferentes distancias del eje neutral, es posible construir diagramas de las tensiones principales a partir de estos valores. Estos diagramas caracterizan el cambio en los esfuerzos principales a lo largo de la altura de la viga.
De igual forma, es posible calcular los valores de esfuerzos cortantes extremos y construir diagramas de estos esfuerzos. En la fig. 46.7, b para una sección transversal rectangular de una viga, en la que actúan un momento flector positivo M y una fuerza transversal Q, apareciendo diagramas de tensiones en las zonas que coinciden con la sección transversal, diagramas de las tensiones principales y tensiones cortantes extremas.
Determinemos para algún punto de la viga la dirección de uno de los esfuerzos principales, y luego tomemos un segundo punto en esta dirección, suficientemente cerca del primero. Habiendo encontrado la dirección del estrés principal para el segundo punto, marcamos el tercer punto de manera similar, etc.
Conectando los puntos encontrados de esta manera, obtenemos la llamada trayectoria de tensiones principales. Dos de estas trayectorias pasan por cada punto, perpendiculares entre sí; uno de ellos representa la trayectoria de los principales esfuerzos de tracción y el otro, los principales de compresión. Las trayectorias de los principales esfuerzos de tracción forman una familia de curvas y las trayectorias de los principales esfuerzos de compresión forman otra familia. La tangente a la trayectoria en cualquier punto da la dirección de la tensión principal correspondiente (de tracción o de compresión) en ese punto.

En la fig. 47.7 muestra una parte de la fachada de una viga con las trayectorias aplicadas de los esfuerzos principales. Todos ellos cortan el eje del haz en ángulos de ±45° y se aproximan a las caras superior e inferior del haz en ángulos de 0 y 90°; esto corresponde a las direcciones de las áreas principales (y las tensiones principales) que se muestran en la Fig. 46.7, a.

fuerza longitudinal 
![]()
![]()
Al derivar fórmulas de cálculo para determinar la tensión normal, se hace la siguiente suposición: el eje longitudinal no cambia su longitud cuando se dobla, las líneas longitudinales se doblan a lo largo del radio. Los contornos de las secciones transversales son planos antes de la carga y permanecen planos después de la carga; las curvas de nivel de las secciones son en todas partes perpendiculares al eje longitudinal.
Hay una capa que no cambia su longitud cuando se dobla: se llama capa neutra.
Al cruzar la capa neutra con una sección transversal, obtenemos una línea neutra.
Con un plegado plano, la capa neutra resulta ser perpendicular al plano de fuerza y, por lo tanto, la línea neutra es perpendicular a la línea de fuerza de la sección.
Elijamos ahora un elemento viga de longitud dx con dos secciones transversales.

La deformación relativa de la fibra es igual a la diferencia entre las longitudes de las fibras ![]()
![]()
Considere una fibra a 0 b 0 perteneciente a la capa normal, su longitud es igual al segmento dx, después de la deformación, el segmento se convierte en un arco a 0 ’b 0 ’=
La fibra de la capa neutra no cambia su longitud durante la deformación => dx=, sustituyendo esta expresión en la fórmula de deformación relativa
de acuerdo con la ley de Hooke, comparando estas expresiones =>, aquí y es la distancia desde la línea neutra hasta el punto donde se determina este voltaje, sustituyendo esta expresión en la expresión del momento: ![]()


![]()
En los casos de flexión transversal, el cálculo de las tensiones normales se realiza según la misma fórmula que para la flexión pura, ya que la diferencia de resultados es prácticamente nula, y el esfuerzo cortante resultante puede alcanzar valores elevados, y se determina durante la flexión mediante las fórmulas de Zhuravsky. 
Determinación del esfuerzo cortante en flexión transversal
Con una sección transversal, fuerzas transversales Q y momentos de flexión, no solo surge la tensión normal, sino también la de corte.
Considere la derivación de la fórmula para determinar los esfuerzos cortantes en una viga con una sección transversal
![]()

Estas suposiciones son válidas si el ancho de la sección b es mucho menor que h.
Marcamos una parte del elemento viga dibujando un plano horizontal mm a una distancia y de la línea neutra
No hay esfuerzos en las caras A 1 A 2 m 2 m 1, C 1 C 2 n 2 n 1 y A 1 A 2 C 2 C 1, porque estas caras son parte de la superficie exterior de la viga.
Es necesario calcular la resultante de tensiones normales distribuidas a lo largo de la cara A 1 C 1 m 1 n 1 sobre un área elemental dF=bd, trazada paralelamente al eje z, a una distancia de éste, actúa una fuerza axial normal ![]()
![]()

Momento estadístico del área encerrada entre el nivel Y y el borde exterior de la viga
![]()
Análogamente, en la cara A 2 C 2 n 2 m 2, la resultante de las tensiones normales será igual a: ![]()
el valor del momento estático del plano recortado será el mismo que en la expresión anterior.
En la cara n 1 n 2 m 1 m 2 actúa la tensión normal, ya que las fibras se presionan entre sí durante la flexión transversal, pero estas tensiones se desprecian como insignificantes para los cálculos de resistencia.
Además, de acuerdo con la ley de emparejamiento de esfuerzos cortantes, los esfuerzos cortantes surgen en la dirección perpendicular a lo largo de la ZPKN
Porque la longitud de la cara n 1 n 2 m 1 m 2 es pequeña, es decir es igual a dx, podemos suponer que están distribuidas uniformemente sobre esta cara.
![]()
Condición de equilibrio paralelepípedo: a 1 a 2 c 2 c 1 n 1 n 2 m 2 m 1

![]()
Si dividimos la igualdad resultante por bdx, entonces: ![]() - fórmula de Zhuravsky,
- fórmula de Zhuravsky,
Lo que le permite determinar la cantidad de esfuerzo cortante durante la flexión transversal en cualquier nivel de la sección transversal
![]()