Parametric voltage regulators are still used to power low-power electronic devices, so you need to be able to calculate them.
Often, when repeating ready-made structures, the operating conditions of which differ from those recommended by the developer, it is required to analyze the operation of a parametric voltage stabilizer to clarify the resistance value of the ballast resistor.
These tasks are solved using the file developed by the author in Microsoft Excel. Two options for calculating a parametric voltage stabilizer and a calculation for analyzing the operating conditions of a zener diode in a finished circuit are given.
The objects of calculation and analysis in the examples are parametric stabilizers of two well-known designs of audio frequency power amplifiers. This is from Interlavka and from Andrey Zelenin A.
Basic ratios for calculating a parametric stabilizer on a zener diode
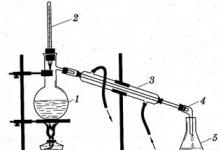
On fig. 1 shows a schematic diagram of a parametric stabilizer: Uin - input unstabilized voltage, Uout \u003d Ust - output stabilized voltage, Ist - current through the zener diode, In - load current, R 0 - ballast (limiting, quenching) resistor.Uin \u003d Ust + (In + Ist) R 0 \u003d Ust + IR 0, (1)
I \u003d Iн + Ist - current flowing through the ballast resistor R 0.

Rice. 1. Scheme of a parametric voltage stabilizer on a zener diode
As can be seen from fig. 1, a parametric stabilizer on a silicon zener diode is a voltage divider, consisting of a ballast resistor R 0 with a linear Volt - current characteristic (CV) and a zener diode VD1, which can be considered as a resistor with a sharply nonlinear IV characteristic.
When the voltage Uin changes, the current through the divider changes, leading to a change in the voltage drop across the resistor R 0, and the voltage across the zener diode, therefore, at the load Rn practically does not change.
A small change in voltage at the load in the range from Ust min to Ust max corresponds to a change in current through the zener diode from Ist min to Ist max. Moreover, the minimum current through the zener diode corresponds to the minimum input voltage and maximum load current, which is achieved with the resistance of the ballast resistor
R 0 \u003d (Uin min-Ust min) / (In max + Ist min). (2)
In turn, the maximum current through the zener diode will flow at the minimum load current and maximum input voltage.
It is easy to find the operating conditions of the stabilizer:
ΔUin=ΔUst+R 0 (ΔIst-ΔIn), (3)
where ΔUin=Uin max-Uin min, ΔUst= Ust max-Ust min, ΔIst=Ist max-Ist min, ΔIn= In max-In min.
For simplicity, let us set ΔUst=0 and analyze expression (3).
The load current range cannot be greater than the zener diode current range, because in this case the right side of the expression becomes negative, and the circuit will not work as a voltage regulator.
If the change in the load current is insignificant, the expression for the operating condition of the stabilizer is simplified:
ΔUin= ΔIstR 0 . (4)
The efficiency of the parametric stabilizer is determined from the expression:
Efficiency \u003d Ust In / (Uin (In + Ist) \u003d 1 / (Nst (1 + Ist / In)), (5)
where Nst=Uin/Ust is the stabilizer transfer coefficient; usually Nst \u003d 1.4 ... 2.
It follows from expression (5) that the lower the stabilizer transfer coefficient and the lower the ratio of the current through the zener diode to the load current, the higher the efficiency.
The main parameter of the voltage stabilizer, by which its quality of work is evaluated, is the stabilization coefficient:
Kst \u003d (ΔUin / Uin) / (ΔUout / Uout) \u003d R 0 Ust / rdUin \u003d R 0 /Nstrd \u003d Kfefficiency, (6)
where rd is the dynamic resistance of the zener diode; Kf is the filtration coefficient.
The first option for calculating the parametric stabilizer
we will carry out for the case when the supply voltage is unstable, and the load resistance is relatively constant.
The initial data for the calculation are: Uout, In, ΔIn, Uin, ΔUin.
To obtain the required output voltage, according to the reference book, we select a zener diode with the parameters: Ust \u003d Uout, Ist max, Ist min, rd.
The required input voltage is calculated based on the extreme optimal transmission coefficients of the stabilizer Nst = 1.4 ... 2, which can also be selected by the user in any required range of Nst:
Ist p \u003d 0.5 (Ist min + Ist max)> In.
Calculate the resistance of the ballast resistor:
R 0 \u003d (Uin - Ust) / (Ist p + In).
We calculate with a double margin the power of the ballast resistor:
Po=2(Ist p+ In) 2 R 0 .
Let's check the selected mode of operation of the stabilizer.
The calculation was made correctly if, with a simultaneous change in Uin by ΔUin and In by ΔIn, the zener diode current does not go beyond Ist max and Ist min:
Ist p max \u003d (Uin + ΔUin- Ust) / (R 0 - (In- ΔIn))<0,8 Iст max;
Ist p min \u003d (Uin - Ust) / (R0- (In + ΔIn))\u003e 1.2 Ist min.
Here, a margin of 20% is taken into account, which is necessary for the reliable operation of the zener diode. The highest operating value of the current through the zener diode, not more than 0.8 of the reference Ist max, adopted in the calculation, is due to considerations of the operational reliability of the device so that the power dissipated on the zener diode is below the limit. To ensure the required stabilization coefficient, the minimum operating value of the current through the zener diode Ist p min is taken in the calculation to be 1.2 times greater than Ist min.
If the obtained values of the currents Istr max and Istr min go beyond the permissible values, then it is necessary to select a different value of Istr p, change the resistance R 0 or replace the zener diode.
We also calculate the stabilizer parameters that determine its quality and efficiency - the stabilization coefficient Kst \u003d (ΔUin / Uin) / (ΔUout / Uout) \u003d R 0 / (rdNst),
efficiency coefficient efficiency = Ust In / (Uin (In + Ist)) \u003d 1 / (Nst (1 + Ist / In)),
and filtration coefficient Kf=Kst/efficiency.
Calculation example No. 1
Let's calculate a parametric voltage stabilizer with the following characteristics: stabilized voltage at the load Un=9 V; load current In=10 mA; change in current in the load ΔIn=2 mA; input voltage change ΔUin=10%.We choose a zener diode of the D814B type, for which Ust \u003d Un \u003d 9 V; rd=10 Ohm; Ist max=36 mA; Ist min=3 mA.
We enter the above information into the corresponding cells of the source data (highlighted in light blue shading) of the “First calculation option” sheet of the Microsoft Excel table “Calculation and analysis of the operation of a parametric voltage stabilizer.xlsx” and immediately we get the calculation results in the calculation cells highlighted in light brown fill:
input voltage Uin=15.0 V; the resistance of the ballast resistor R 0 =240 Ohm, the power of the ballast resistor with a double margin Po=0.3 W; Kst=15.0, efficiency=24%, Kf=62.5 (see Fig. 2).

Rice. 2. Printing from the screen of calculation example No. 1
We select a resistor with a resistance of 240 ohms with a power of 0.5 watts.
Suppose that at the input of the stabilizer there are ripples of an alternating voltage with an amplitude Up in = 0.1 V = 100 mV. The amplitude of the ripples at the output of the stabilizer will be Up st \u003d Up in / Kf \u003d 100 / 62.5 \u003d 1.6 mV.
Calculation example No. 2
Let's calculate the parametric stabilizer for supply voltages Up=Uin=±25 V; ±35 V and ±45 V.The calculation is performed for a parametric stabilizer of positive polarity (R5, VD1, C2), since another stabilizer of negative polarity (R6, VD2, C4) differs only in the direction of switching on the zener diode.
Let's prepare the initial data: stabilized voltage at the load Un=12 V, current in the load In=(12-0.5)/R2=11.5/10=1.15 mA, ΔIn=0.115 mA, input voltage change ΔUin=10 %.
Let's choose a zener diode BZX55C12, which has the following parameters: Ust = Un = 12 V; rd=20 Ohm; Ist max=32 mA; Ist min=5 mA.
The calculation results are shown in fig. 3; for Up=±25 V R5=R6=1.3 kOhm (0.25 W); for Up=±35 V R5=R6=2.4 kOhm (0.5 W); for Up=±45 V R5=R6=3.6 kOhm (1 W).

Rice. 3. Calculation of parametric stabilizers for the Green Lanzar amplifier
The second option for calculating the parametric stabilizer
as initial data, it uses the limiting values of the current in the load Iн min and Iн max, which, with Iн min=0, allows us to provide for the idling mode of the stabilizer. For a constant load, choose In max \u003d In min.
So, the initial data are: stabilized load voltage Uout, load currents In min, In max, rated input voltage Uin and its deviations ΔUin n and ΔUin in.
The parameters of the zener diode are the same as in the previous calculation: Ust = Uout, Ist max, Ist min, rd.
We calculate the maximum and minimum values \u200b\u200bof the operating current of the zener diode:
Ist p max=0.8 Ist max,
Ist p min=1.2 Ist min.
If the stabilizer should operate in idle mode (Iн min=0), select Ist p min=Ist min.
We check the suitability of the stabilizer diode selected for voltage stabilization within the specified limits of the load current and supply voltage:
(Ist p max + In min) (1- ΔUin n) - (Ist min + In max) (1+ ΔUin in)> 0,
where ΔUin n=(Uin-Uin min)/ Uin, ΔUin in=(Uin max-Uin)/ Uin.
If the inequality is not met, you need:
use a more powerful zener diode;
set smaller values ΔUin n and ΔUin in;
reduce In max or increase In min.
The rated voltage Uin, which the rectifier must provide, is calculated by the formula:
Uin \u003d Ust [(Ist r max + I n min) - (Ist r min + I n max)] / [(Ist r max + I n min) (1- ΔUin n) - (Ist r min + I n max) (1+ΔUin c)].
Ballast resistor resistance:
R 0 \u003d Uin (ΔUin in + ΔUin n) / [(Ist r max + In min) - (Ist r min + In max)].
We also calculate the power of the resistor with a double margin:
Po=2(Uin(1+ ΔUin n)- Ust) 2 /R 0 .
According to the formulas given in the first version of the calculation, we find Kst, efficiency and Kf.
Calculation example No. 3
Let's calculate a parametric voltage stabilizer with the following characteristics: stabilized voltage at the load Un=9 V; current In min =0, In max =10 mA; change in input ΔUin n=10%, ΔUin in=15%.We choose a zener diode of type D814B, for which Ust \u003d Un; rd=10 Ohm; Ist max=36 mA, Ist min=3 mA.
After entering the initial data in the sheet of the table “Second calculation option”, we obtain the following results (Fig. 4):
Uin \u003d 14 V, R 0 \u003d 221 Ohm, Po \u003d 0.45 W, Kst \u003d 14.2.

Rice. 4. Screenshot of the parametric stabilizer idle
We select a resistor with a resistance of 220 ohms with a power of 0.5 watts.
Analysis of the operation of a parametric stabilizer
The initial data of the analysis are as follows: Un, In, ΔIn, ΔUin, R 0 .Also, the analysis requires the parameters of the zener diode: Ust \u003d Un, rd, Ist max and Ist min.
The analysis is reduced to calculating the operating current of the zener diode Ist p \u003d (Uin-Ust) / R 0 -In; transmission coefficient Nst = Uin/Ust; power Po of the ballast resistor, stabilization factor Kst, efficiency and filtering factor Kph.
It is important to check the operating mode of the zener diode in the stabilizer circuit, which is performed using formulas similar to those given in the first calculation option.
Analysis Example #1
Let's analyze the ratings of the ballast resistors R3 and R4 of the compensation voltage stabilizers of the Lanzar amplifier, depending on the supply voltage used.The range of supply voltages of the amplifier is declared from Up \u003d ± 30 V to ± 65 V, while the resistance of the ballast resistors R 0 \u003d R3 \u003d R4 \u003d 2.2 kOhm (1 W) is indicated on the circuit diagram.
In another publication, it is recommended to choose the resistance value of the ballast resistors depending on the amplifier supply voltage according to the formula R 0 = (Up-15) / I, where I = 8 ... 10 mA. In table 1, the calculation is made according to the indicated formula for the range of supply voltages of the amplifier with a step of 5 V.

Initial data for analysis: stabilized load voltage Un=15 V, load current In=(15-0.5)/R5=14.5/6.8=2.13 mA, ΔIn=0.213 mA, change in input voltage ΔUin=10%.
We choose a zener diode 1N4744A, which has the following parameters: Ust \u003d Un \u003d 15 V; rd=14 Ohm; Ist max=61 mA; Ist min=5 mA.
An analysis of the operation of parametric stabilizers in the Lanzar amplifier showed that the minimum stabilizer current Istr min was selected at the limit with a margin of only 3 ... 14% instead of the required 20% (Fig. 5).

Rice. Fig. 5. Operating modes of stabilizers in the Lanzar amplifier, depending on the selected supply voltage
Using the data analysis tool of the Microsoft Excel spreadsheet "Parameter Selection", we will specify the resistance of the ballast resistors. To do this, go to the cell with the formula for Ist p min (cell C26) and choose from the menu Data -> « What-if analysis»-> Parameter selection.
Set in cell C26 value 6.0 (margin 20% of Ist min), changing the value of the cell in which the resistance of the ballast resistor is entered ( $C$15).
We get R 0 \u003d 1.438 kOhm. Let's put in this cell the nearest resistance value from the standard series R 0 =1.3 kOhm.
Having carried out the indicated operation in the table for all values of the supply voltages, we obtain the following result (Fig. 6).

Rice. 6. Refinement of the operating modes of the parametric stabilizers of the Lanzar amplifier
The results of the analysis are also summarized in Table 2.

The power of resistors for amplifier supply voltages from ±30 V to ±40 V is 0.5 W, for other voltages it is 1 W.
Outcome
It is necessary to calculate even such a simple device as a parametric voltage stabilizer. The choice of the value of the resistance of the ballast resistor "by eye" can cause design errors that will not be immediately noticed.Before assembling the design you like, it is advisable to analyze and, if necessary, clarify the operation mode of the zener diode of the parametric stabilizer using the proposed spreadsheets in Microsoft Excel.
As you know, no electronic device works without a suitable power source. In the simplest case, a conventional transformer and a diode bridge (rectifier) with a smoothing capacitor can act as a power source. However, it is not always at hand to have a transformer for the desired voltage. And even more so, such a power supply cannot be called stabilized, because the voltage at its output will depend on the voltage in the network.
A solution to these two problems is to use ready-made stabilizers, for example,. They are convenient to use, but again, they are not always at hand. Another option is to use a parametric stabilizer on a zener diode and a transistor. Its diagram is shown below.
Stabilizer circuit on 1 transistor
VD1-VD4 in this circuit is a conventional diode bridge that converts AC voltage from a transformer to DC. Capacitor C1 smooths out voltage ripples, turning the voltage from pulsating to constant. In parallel with this capacitor, it is worth putting a small film or ceramic capacitor to filter high-frequency ripples, because. at high frequency, the electrolytic capacitor does not do its job well. The electrolytic capacitors C2 and C3 in this circuit are for the same purpose - smoothing out any ripples.
The chain R1 - VD5 serves to form a stabilized voltage, the resistor R1 in it sets the stabilization current of the zener diode. Resistor R2 is load. The transistor in this circuit absorbs the entire difference between the input and output voltage, so a decent amount of heat is dissipated on it. This circuit is not designed to connect a powerful load, but, nevertheless, the transistor should be screwed to the radiator using heat-conducting paste.
The voltage at the output of the circuit depends on the choice of the zener diode and the value of the resistors. The table below shows the values of the elements for obtaining 5, 6, 9, 12, 15 volts at the output.

Instead of the KT829A transistor, you can use imported analogues, for example, TIP41 or BDX53. It is permissible to install a diode bridge any suitable for current and voltage. In addition, you can assemble it from individual diodes. Thus, when using a minimum of parts, a workable voltage regulator is obtained, from which other electronic devices that consume a small current can be powered. Photo of the stabilizer I assembled.
So, on the right is a diagram of a simple transistor voltage regulator.
Designations:
- I to - collector current of the transistor
- I n - load current
- I b - transistor base current
- I R - current through the ballast resistor
- U in - input voltage
- U out - output voltage (voltage drop across the load)
- U st - voltage drop across the zener diode
- U be - voltage drop at the p-n junction of the base-emitter of the transistor
How does such a stabilizer work and how does its work differ from work? Yes, their work is almost the same - the voltage at the output of the circuit remains stable as a result of the presence of sections on the current-voltage characteristics (zener diode and p-n junction of the base-emitter of the transistor) in which the voltage drop weakly depends on the current. That is, like all parametric stabilizers, stability is achieved by the internal properties of the components.
Indeed, as can be seen from the figure, the voltage drop across the load is equal to the difference in voltage drops across the zener diode and at the p-n junction of the BE transistor. Since the voltage drop across the zener diode weakly depends on the current (in the working area it is equal to the stabilization voltage), the voltage drop at the forward-biased p-n junction also weakly depends on the current (for a silicon transistor, it can be taken approximately the same as for a conventional silicon diode - approximately 0, 6 volts), it turns out that the output voltage is also constant.
Now let's add some math.
With the voltage at the load (output voltage), everything is already clear: U out \u003d U st -U be, let's calculate R 0 and the area of normal operation of the stabilizer. But first, let's draw two pictures side by side - a piece of our stabilizer circuit and a piece of the simplest parametric stabilizer on a zener diode:

It looks like it, doesn't it? Moreover, the reasoning and the relationships derived from them for calculating R 0 and the area of normal operation are also very similar.
An equation describing currents and voltages for the piece of our stabilizer circuit torn out above:
U in \u003d U st + I R R 0, given that I R \u003d I st + I b, we get
U in \u003d U st + (I st + I b) R 0 (1)
For normal operation of the stabilizer (so that the voltage on the zener diode is always in the range from U st min to U st max), it is necessary that the current through the zener diode is always in the range from I st min to I st max. The minimum current through the zener diode will flow at the minimum input voltage and maximum base current of the transistor. Knowing this, we find ballast resistor resistance:
R 0 \u003d (U in min -U st min) / (I b max + I st min) (2)
Considering that in our case, when the transistor is connected according to a common collector circuit, the base current is related to the emitter current by the ratio I e \u003d I b (h 21E + 1), the emitter current is equal to the load current (because we have the load is on), and the voltage on the zener diode in the operating mode changes slightly (instead of U st min, we just take U st), we get that
R 0 \u003d (U in min -U st) / (I n max / (h 21E +1) + I st min) (3)
h 21E +1 is the current gain for a circuit with a common collector (h 21K), but since h 21E is usually quite large, the “+1” term is often thrown out and it is believed that h 21K \u003d h 21E, then the formula (3 ) becomes a little easier:
R 0 \u003d (U in min -U st) / (I n max / h 21E + I st min)
The maximum current through the zener diode will flow at the minimum base current of the transistor and the maximum input voltage. Considering this and what was said above regarding the minimum current through the zener diode, using equation (1) you can find the area of \u200b\u200bnormal operation of the stabilizer:
Rearranging this expression, we get:
Or, in other words:
If we assume that the minimum and maximum stabilization voltage (U st min and U st max) differ slightly (the first term on the right side can be considered equal to zero), and also that I n \u003d I e \u003d I b h 21E ("+ 1 "- throw out), then equation describing the area of normal operation of the stabilizer, takes the following form:
This formula clearly shows the advantage of such a transistor stabilizer over a parametric stabilizer on a zener diode - other things being equal, the output current of a transistor stabilizer can vary over a wider range.
For example, let's take the KS147A zener diode again (I st \u003d 3..53mA), and estimate what maximum current we can count on when the voltage drops from 6..10V to 5V, provided that the output current can vary from zero to I max. Take the transistor KT815A (h 21E \u003d 40). Having jointly solved the system of equations (3), (4), we obtain R 0 about 110 Ohm and the maximum current is about 550 mA.
However, it is worth noting that the instability of the output voltage in this case will be even worse, since now the instability of the voltage drop at the p-n junction of the transistor will be added to the instability of the voltage at the zener diode. Plus, we have not yet taken into account that the output voltage will be less than on the zener diode by the amount of voltage drop at the p-n junction, so for good we should have taken the zener diode not by 4.7V, but by 5.1 or even 5.6 Volt (I specifically took for example the same zener diode as in, so that you can see more clearly how much the load current will differ with the same zener diode).
Actually, the methods of dealing with instability are completely similar here - you need to somehow reduce the voltage instability at the zener diode. To do this, you can, like last time, take a narrower working section of the CVC of the zener diode. This will naturally also lead to a narrowing of the area of normal operation (because the range of change in the operating current of the zener diode will decrease), but in this case, when the area of normal operation is already wider than that of the parametric stabilizer on the zener diode (by about h 21E times), we are quite we can afford to give up part of the output current range and / or part of the input voltage range in order to increase the stability of the output voltage.

You can further increase the area of \u200b\u200bnormal operation if you use two transistors connected according to the Darlington or Shiklai circuit (figure on the left). In this case, h 21E will be much larger.
Well, the very squeak is to do it, since the gain of the op-amp is not just larger, but significantly, much, many - many times greater than that of any transistor (respectively, we will be able to change the current through the zener diode in an even narrower range, we will get an even smaller change voltage on it and, as a result, an even more stable output voltage).
There is another option - instead of the usual zener diode, you can take an integral zener diode, for example, TL431. In this case, in addition to much less instability, we also get the ability to control the output voltage.
For a snack, I’ll say that with a slight movement of the hand, such a voltage stabilizer can be turned into a current stabilizer (you just need to stabilize the voltage not on the load, but on a special current-measuring resistor).
Until recently, parametric voltage stabilizers were used to power low-power cascades of electronic equipment. It is now much cheaper and more efficient to use low-noise compensation regulators like the ADP3330 or ADM7154. Nevertheless, parametric stabilizers are already used in a number of equipment already being produced, so it is necessary to be able to calculate them. The most common parametric stabilizer circuit is shown in Figure 1.
Figure 1. Scheme of a parametric stabilizer
This figure shows a positive voltage regulator circuit. If you want to stabilize the negative voltage, then the zener diode is placed in the opposite direction. The stabilization voltage is completely determined by the type of zener diode.
The calculation of the stabilizer in this way is reduced to the calculation of the resistor R 0 . Before starting its calculation, it is necessary to determine the main destabilizing factor:
- input voltage;
- consumption current.
Unstable input voltage at a stable current consumption is usually present in voltage reference sources for analog-to-digital and digital-to-analog converters. For a parametric stabilizer that feeds a certain piece of equipment, it is necessary to take into account the change in the output current. In the circuit shown in Figure 1, with a constant input voltage, the current I will always be stable. If the load consumes less current, then its excess will go into the zener diode.
I = I st + I n (1)Therefore, the maximum load current cannot exceed the maximum current of the zener diode. If the input voltage is not constant (and this situation is very common), then the allowable range of load current variation is further reduced. Resistor resistance R 0 is calculated according to Ohm's law. The calculation uses the minimum value of the input voltage.
The maximum input voltage range can be determined by Kirchhoff's law. After slight transformations, it can be reduced to the following formula:
(3)
Thus, the calculation of the parametric stabilizer is quite simple. This is what makes it attractive. However, when choosing the type of stabilizer, one should keep in mind the fact that the zener diode (but not the stabistor) is a source of noise. Therefore, the described stabilizer should not be used in critical units of radio equipment. I emphasize once again that when designing new equipment, small-sized low-noise compensation stabilizers, such as the ADP7142, are better suited as a secondary power source.
Literature:
- Sazhnev A.M., Rogulina L.G., Abramov S.S. “Power supply of devices and communication systems”: Textbook / GOU VPO SibGUTI. Novosibirsk, 2008 - 112 p.
- Aliev I.I. Electrotechnical reference book. - 4th ed. correct - M.: IP Radio Soft, 2006. - 384 p.
- Geytenko E.N. Sources of secondary power supply. Circuitry and calculation. Tutorial. - M., 2008. - 448 p.
- Power supply of devices and telecommunications systems: Textbook for universities / V.M. Bushuev, V.A. Deminsky, L.F. Zakharov and others - M., 2009. – 384 p.
- Parametric voltage stabilizers. Calculation of the simplest parametric stabilizer on a zener diode (http://www.radiohlam.ru/)
Stabilizers are used to smooth out voltage ripples and constant current at the output of the power supply. As a rule, the stabilizer is based on a zener diode. A zener diode is a semiconductor device that has the property of voltage stabilization. Unlike a conventional diode, it works in reverse polarity (plus is applied to the cathode), in the avalanche breakdown mode. Due to this property of the zener diode, the voltage on it, and therefore on the load, practically does not change. The figure below shows a diagram of a simple stabilizer.
Such a stabilizer is suitable for powering low-power devices.
The principle of operation of the stabilizer on the zener diode
A capacitor is needed to smooth out voltage ripples, it is called a filtering capacitor. A resistor is needed to smooth out current ripples and is called a quenching resistor. The zener diode stabilizes the voltage across the load. For normal operation of this circuit, the supply voltage must be more than 40 ... 50%. The zener diode should be selected for the voltage and current we need.
Stabilizer on one transistor
To power a load of greater power, a transistor is added to the circuit. An example circuit is shown below.

The principle of operation of the stabilizer on a single transistor
The chain of R1 and VT1 is already familiar to us from the previous circuit, this is the simplest stabilizer, it sets the stabilized voltage based on the transistor VT2. The transistor, in turn, acts as a current amplifier and is the control element in this circuit. For example, when the input voltage increases, the output voltage will tend to increase. This leads to a decrease in voltage at the emitter junction of the transistor VT2, which leads to its closure. In this case, the voltage drop in the emitter-collector section increases so much that the voltage across the zener diode decreases to its original level. When the voltage drops, the stabilizer reacts in the reverse order.
Transistor stabilizer with short circuit protection
In the practice of a radio amateur, there are mistakes and a short circuit occurs. To reduce the consequences as a result of a short circuit, consider a stabilizer circuit for two fixed voltages and with short circuit protection.

As you can see, transistor V4, diodes V6 and V7 are added to this circuit, and a parametric stabilizer consisting of resistor R1, diodes V2, V3 is equipped with switch S2.
The principle of operation of the stabilizer protection
This circuit is designed for a short circuit operation current of 250 ... 300 mA, until it is exceeded, the current will pass through a voltage divider consisting of a V7 diode and a resistor R3. By selecting this resistor, you can adjust the protection threshold. Diode V6 will be closed and will not have any effect on work. When the protection is triggered, diode V7 will close, and diode V6 will open and shunt the zener diode connections, while transistors V4 and V5 will close. The load current will drop to 20…30 mA. Transistor V5 should be installed on the heat sink.
Stabilizer with adjustable output voltage
In the repair or adjustment of electronic devices, it is necessary to have a power supply with adjustable output voltage. Schematic diagram of voltage regulated stabilizers is presented below.

The principle of operation of the stabilizer with voltage regulation
Parametric stabilizer consisting of R2 and V2 stabilize the voltage across the variable resistor R3. The voltage from this resistor is supplied to the control transistor. This transistor is connected according to the emitter follower circuit, the load of which is the resistor R4. The voltage from the resistor R4 is supplied to the regulating transistor V4, the load of which is already our powered device. Voltage regulation is carried out by a variable resistor R3, if the resistor slider is in the minimum position according to the circuit, then the voltage to open transistors V3 and V4 is not enough and the output will have a minimum voltage. When the engine rotates, the transistors begin to open, which increases the voltage on the load. With an increase in load current, the voltage drop across the resistor R1 and the lamp H1 starts to light up, at a current of 250 mA a dim glow is observed, and at a current of 500 mA and above it is bright. Transistor V4 should be installed on the heat sink. With an increased load of more than 500 mA, you should turn off the power supply as soon as possible, since with a long maximum load, the diodes in the rectifier bridge and the V4 transistor fail.
These circuits, when properly assembled, do not need to be adjusted. They can also be upgraded to higher current and voltage. By selecting radio elements with the parameters we need.
That's all. If you have any comments or suggestions on this article, please write to the site administrator.