is differentiable on the interval (a, c). Then there is a tangent to the graph of the function at any point 
this graph ( 
), and the tangent is not parallel to the OY axis, since its slope equal to 
, of course.
definition
on (a, c) has a release pointing down (up) if it is located not below (not above) any tangent to the graph of the function on (a, c). 
(
) at all points of this interval, then the curve that is the graph of the function is convex (concave) on this interval.
is called the inflection point of the function graph, if at the point 
the graph has a tangent, and there is such a neighborhood of the point 
, within which the graph of the function on the left and right of the point has different directions of convexity.
it is obvious that at the inflection point the tangent crosses the graph of the function, since on one side of this point the graph lies above the tangent, and on the other - under it, i.e., in the vicinity of the inflection point, the graph of the function passes geometrically from one side of the tangent to the other and "bends" through it. This is where the name "inflection point" comes from.
continuous second derivative. Then 
.
has no inflection point at (0, 0), although 
at 
. Therefore, the equality of the second derivative to zero is only a necessary condition for the inflection. 
has different signs to the left and right of the point , then the graph has an inflection at the point . 
has a second derivative in some neighborhood of the point , except for the point itself, and there is a tangent to the graph of the function at the point 
. Then, if within the indicated neighborhood it has different signs to the left and to the right of the point , then the graph of the function has an inflection at the point . 
convexity, concavity, inflection points. 
, 
=
does not exist at 
)
)
or near discontinuity points of the 2nd kind, it often turns out that the graph of a function approaches one or another straight line as close as one likes. Such lines are called.
definition 1.
is called an asymptote of the curve L if the distance from the point of the curve to this line tends to zero as the point moves away along the curve to infinity. There are three types of asymptotes: vertical, horizontal, oblique. 
is called the vertical asymptote of the function graph if at least one of the one-sided limits is equal to 
, i.e., or 
has a vertical asymptote 
, because 
, a 
.
if 
.
.
(
) is called the oblique asymptote of the graph of the function for 
if 
; 
.
; x=0 – vertical asymptote
.
is the oblique asymptote. 
and plot it. 
function neither even nor odd-
-
+
+
y
-4
t r.
0
Conclusion.
An important feature of the considered method is that it is based primarily on the detection and study of characteristic features in the behavior of the curve. Places where the function changes smoothly are not studied in particular detail, and there is no need for such a study. But those places where the function has any peculiarities in behavior are subject to full research and the most accurate graphic representation. These features are the points of maximum, minimum, points of discontinuity of the function, etc.
Determination of the direction of concavity and inflections, as well as the indicated method of finding asymptotes, make it possible to study functions in even more detail and get a more accurate idea of their graphs.
Function Graph y=f(x) called convex on the interval (a;b), if it is located below any of its tangents on this interval.
Function Graph y=f(x) called concave on the interval (a;b), if it is located above any of its tangents in this interval.
The figure shows a curve convex on (a;b) and concave to (b;c).
Examples.
Consider a sufficient sign that allows you to determine whether the graph of a function in a given interval will be convex or concave.
Theorem. Let be y=f(x) differentiable by (a;b). If at all points of the interval (a;b) second derivative of the function y = f(x) negative, i.e. f ""(x) < 0, то график функции на этом интервале выпуклый, если же f""(x) > 0 is concave.
Proof. Assume for definiteness that f""(x) < 0 и докажем, что график функции будет выпуклым.
Take on the function graph y = f(x) arbitrary point M0 with abscissa x0 Î ( a; b) and draw through the point M0 tangent. Her equation. We must show that the graph of the function on (a;b) lies below this tangent, i.e. with the same value x curve ordinate y = f(x) will be less than the ordinate of the tangent.
So the equation of the curve is y = f(x). Let us denote the tangent ordinate corresponding to the abscissa x. Then . Therefore, the difference between the ordinates of the curve and the tangent at the same value x will .
Difference f(x) – f(x0) transform according to the Lagrange theorem, where c between x and x0.
Thus,
We again apply the Lagrange theorem to the expression in square brackets: , where c 1 between c 0 and x0. According to the theorem f ""(x) < 0. Определим знак произведения второго и третьего сомножителей.
Thus, any point of the curve lies below the tangent to the curve for all values x and x0 Î ( a; b), which means that the curve is convex. The second part of the theorem is proved similarly.
Examples.
The point on the graph of a continuous function that separates its convex part from the concave part is called inflection point.
Obviously, at the inflection point, the tangent, if it exists, intersects the curve, because on one side of this point, the curve lies under the tangent, and on the other side, above it.
Let us define sufficient conditions for a given point of the curve to be an inflection point.
Theorem. Let the curve be defined by the equation y = f(x). If a f ""(x 0) = 0 or f ""(x 0) does not exist and when passing through the value x = x0 derivative f ""(x) changes sign, then the point of the graph of the function with the abscissa x = x0 there is an inflection point.
Proof. Let be f ""(x) < 0 при x < x0 and f ""(x) > 0 at x > x0. Then at x < x0 the curve is convex, and x > x0- concave. Hence the point A, lying on the curve, with abscissa x0 there is an inflection point. Similarly, we can consider the second case, when f ""(x) > 0 at x < x0 and f ""(x) < 0 при x > x0.
Thus, inflection points should be sought only among those points where the second derivative vanishes or does not exist.
Examples. Find the inflection points and determine the intervals of convexity and concavity of the curves.
ASYMPTOTS OF THE GRAPH OF A FUNCTION
When investigating a function, it is important to establish the shape of its graph with an unlimited removal of the graph point from the origin.
Of particular interest is the case when the graph of a function, when its variable point is removed to infinity, indefinitely approaches a certain straight line.
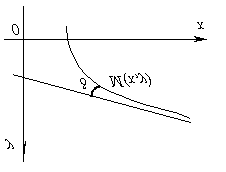
Direct called asymptote function graph y = f(x) if the distance from the variable point M graph to this line when the point is removed M to infinity tends to zero, i.e. the point of the graph of the function, as it tends to infinity, must approach the asymptote indefinitely.
The curve can approach its asymptote, remaining on one side of it or on different sides, intersecting the asymptote an infinite number of times and moving from one side to the other.
If we denote by d the distance from the point M curve to the asymptote, it is clear that d tends to zero as the point is removed M to infinity.
We will further distinguish between vertical and oblique asymptotes.
VERTICAL ASYMPTOTS
Let at x→ x0 either side of the function y = f(x) indefinitely increases in absolute value, i.e. or or 
. Then it follows from the definition of the asymptote that the line x = x0 is an asymptote. The converse is also obvious if the line x = x0 is an asymptote, so .
Thus, the vertical asymptote of the graph of the function y = f(x) is called a line if f(x)→ ∞ under at least one of the conditions x→ x0– 0 or x → x0 + 0, x = x0
Therefore, to find the vertical asymptotes of the graph of the function y = f(x) need to find those values x = x0, at which the function goes to infinity (suffers an infinite discontinuity). Then the vertical asymptote has the equation x = x0.
Examples.
SLANT ASYMPTOTS
Since the asymptote is a straight line, then if the curve y = f(x) has an oblique asymptote, then its equation will be y = kx + b. Our task is to find the coefficients k and b.
Theorem. Straight y = kx + b serves as an oblique asymptote at x→ +∞ for the graph of the function y
= f(x) if and only if 
. A similar statement is true for x → –∞.
Proof. Let be MP- the length of the segment equal to the distance from the point M to the asymptote. By condition . Denote by φ the angle of inclination of the asymptote to the axis Ox. Then from ΔMNP follows that . Since φ is a constant angle (φ ≠ π/2), then , but
Instruction
The inflection points of the function must belong to the domain of its definition, which must be found first. A function graph is a line that can be continuous or have breaks, decrease or increase monotonically, have minimum or maximum points (asymptotes), be convex or concave. A sharp change in the last two states is called an inflection.
A necessary condition for the existence of an inflection of the function is that the second is equal to zero. Thus, having differentiated the function twice and equating the resulting expression to zero, one can find the abscissas of possible inflection points.
This condition follows from the definition of the properties of convexity and concavity of the function graph, i.e. negative and positive values of the second derivative. At the inflection point, there is a sharp change in these properties, which means that the derivative passes the zero mark. However, equality to zero is still not enough to indicate an inflection point.
There are two sufficient conditions that the abscissa found at the previous stage belongs to the inflection point: Through this point, you can draw a tangent to the function. The second derivative has different signs to the right and left of the supposed inflection point. Thus, its existence at the point itself is not necessary, it is enough to determine that it changes sign at it. The second derivative of the function is zero, but the third one is not.
The first sufficient condition is universal and is used more often than others. Consider an illustrative example: y = (3 x + 3) ∛ (x - 5).
Solution.Find the domain of definition. In this case, there are no restrictions, therefore, it is the entire space of real numbers. Calculate the first derivative: y' = 3 ∛ (x - 5) + (3 x + 3) / ∛ (x - 5)².
Pay attention to the appearance of the fraction. It follows from this that the domain of definition of the derivative is limited. The point x = 5 is punctured, which means that a tangent can pass through it, which partly corresponds to the first criterion for the sufficiency of the inflection.
Determine one-sided limits for the resulting expression at x → 5 - 0 and x → 5 + 0. They are equal to -∞ and +∞. You proved that a vertical tangent passes through the point x=5. This point may be an inflection point, but first calculate the second derivative: - 5)^5 = (2 x - 22)/∛(x - 5)^5.
Omit the denominator, because you have already taken into account the point x = 5. Solve the equation 2 x - 22 = 0. It has a single root x = 11. The last step is to confirm that the points x = 5 and x = 11 are inflection points. Analyze the behavior of the second derivative in their vicinity. Obviously, at the point x = 5, it changes sign from “+” to “-”, and at the point x = 11, vice versa. Conclusion: both points are inflection points. The first sufficient condition is satisfied.
With an online calculator, you can find inflection points and convexity intervals of a function graph with the design of the solution in Word. Whether a function of two variables f(x1,x2) is convex is decided using the Hessian matrix.
Function entry rules:
The direction of the convexity of the graph of the function. Inflection points
Definition: A curve y=f(x) is called downward convex in the interval (a; b) if it lies above the tangent at any point of this interval.Definition: Curve y=f(x) is called upward convex in the interval (a; b) if it lies below the tangent at any point of this interval. 
Definition: The intervals in which the graph of the function is convex up or down are called the intervals of the convexity of the graph of the function.
Convexity downwards or upwards of the curve, which is the graph of the function y=f(x) , is characterized by the sign of its second derivative: if in some interval f’’(x) > 0, then the curve is convex downwards on this interval; if f''(x)< 0, то кривая выпукла вверх на этом промежутке.
Definition: The point of the graph of the function y=f(x) that separates the convexity intervals of the opposite directions of this graph is called the inflection point. 
Only critical points of the second kind can serve as inflection points; points belonging to the domain of the function y = f(x) , at which the second derivative f''(x) vanishes or breaks.
The rule for finding inflection points of the function graph y = f(x)
- Find the second derivative f''(x) .
- Find critical points of the second kind of the function y=f(x) , i.e. the point at which f''(x) vanishes or breaks.
- Investigate the sign of the second derivative f''(x) in the intervals into which the found critical points divide the domain of the function f(x) . If, in this case, the critical point x 0 separates the convexity intervals of opposite directions, then x 0 is the abscissa of the inflection point of the function graph.
- Compute function values at inflection points.
Example 1 . Find the convexity gaps and inflection points of the following curve: f(x) = 6x 2 –x 3 .
Solution: Find f '(x) = 12x - 3x 2 , f ''(x) = 12 - 6x.
Let's find the critical points by the second derivative by solving the equation 12-6x=0 . x=2 . 
f(2) = 6*2 2 - 2 3 = 16
Answer: The function is upward convex for x∈(2; +∞) ; the function is downward convex for x∈(-∞; 2) ; inflection point (2;16) .
Example 2 . Does the function have inflection points: f(x)=x 3 -6x 2 +2x-1
Example 3 . Find the intervals where the function graph is convex and convex: f(x)=x 3 -6x 2 +12x+4
To determine the convexity (concavity) of a function on a certain interval, the following theorems can be used.
Theorem 1. Let the function be defined and continuous on the interval and have a finite derivative . For a function to be convex (concave) in , it is necessary and sufficient that its derivative decreases (increases) on this interval.
Theorem 2. Let the function be defined and continuous together with its derivative on and have a continuous second derivative inside . For the convexity (concavity) of the function in it is necessary and sufficient that inside
Let us prove Theorem 2 for the case of convexity of the function .
Need. Let's take an arbitrary point. We expand the function near the point in a Taylor series
The equation of a tangent to a curve at a point having an abscissa:
Then the excess of the curve over the tangent to it at the point is equal to
Thus, the remainder is equal to the excess of the curve over the tangent to it at the point . Due to continuity, if 
, then also for , belonging to a sufficiently small neighborhood of the point , and therefore, obviously, for any different from the value of , belonging to the indicated neighborhood.
This means that the graph of the function lies above the tangent and the curve is convex at an arbitrary point.
Adequacy. Let the curve be convex on the interval . Let's take an arbitrary point.
Similarly to the previous one, we expand the function near the point in a Taylor series
The excess of the curve over the tangent to it at the point having the abscissa , defined by the expression is equal to
Since the excess is positive for a sufficiently small neighborhood of the point , the second derivative is also positive. As we strive, we obtain that for an arbitrary point .
Example. Investigate for convexity (concavity) function .
Its derivative 
increases on the entire real axis, so by Theorem 1 the function is concave on .
Its second derivative 
, therefore, by Theorem 2, the function is concave on .
3.4.2.2 Inflection points
Definition. inflection point graph of a continuous function is called the point separating the intervals in which the function is convex and concave.
It follows from this definition that the inflection points are the points of the extremum point of the first derivative. This implies the following assertions for the necessary and sufficient inflection conditions.
Theorem (necessary inflection condition). In order for a point to be an inflection point of a twice differentiable function, it is necessary that its second derivative at this point be equal to zero ( 
) or did not exist.
Theorem (sufficient condition for inflection). If the second derivative of a twice differentiable function changes sign when passing through a certain point, then there is an inflection point.
Note that the second derivative may not exist at the point itself.
The geometric interpretation of the inflection points is illustrated in fig. 3.9
In a neighborhood of a point, the function is convex and its graph lies below the tangent drawn at this point. In the neighborhood of a point, the function is concave and its graph lies above the tangent drawn at this point. At the inflection point, the tangent divides the graph of the function into regions of convexity and concavity.
3.4.2.3 Examining a function for convexity and the presence of inflection points
1. Find the second derivative.
2. Find points at which the second derivative or does not exist.
Rice. 3.9.
3. Examine the sign of the second derivative to the left and right of the found points and draw a conclusion about the intervals of convexity or concavity and the presence of inflection points.
Example. Investigate the function for convexity and the presence of inflection points.
2. The second derivative is equal to zero at .
3. The second derivative changes sign at , so the point is the inflection point.
On the interval , then the function is convex on this interval.
On the interval , then the function is concave on this interval.
3.4.2.4 General scheme for the study of functions and plotting
When studying a function and plotting its graph, it is recommended to use the following scheme:
- Find the scope of the function.
- Investigate the function for even - odd. Recall that the graph of an even function is symmetrical about the y-axis, and the graph of an odd function is symmetrical about the origin.
- Find vertical asymptotes.
- Explore the behavior of a function at infinity, find horizontal or oblique asymptotes.
- Find extrema and intervals of monotonicity of the function.
- Find the convexity intervals of the function and the inflection points.
- Find points of intersection with coordinate axes.
The study of the function is carried out simultaneously with the construction of its graph.
Example. Explore Function 
and plot it.
1. Function scope - .
2. The function under study is even 
, so its graph is symmetrical about the y-axis.
3. The denominator of the function vanishes at , so the graph of the function has vertical asymptotes and .
The points are discontinuity points of the second kind, since the limits on the left and right at these points tend to .
4. Behavior of the function at infinity.
Therefore, the graph of the function has a horizontal asymptote.
5. Extremes and intervals of monotonicity. Finding the first derivative
For , therefore, the function decreases in these intervals.
For , therefore, the function increases in these intervals.
For , therefore, the point is a critical point.
Finding the second derivative
Since , then the point is the minimum point of the function .
6. Convexity intervals and inflection points.
Function at 
, so the function is concave on this interval.
The function at , means that the function is convex on these intervals.
The function never vanishes, so there are no inflection points.
7. Points of intersection with the coordinate axes.
The equation , has a solution , which means the point of intersection of the graph of the function with the y-axis (0, 1).
The equation has no solution, which means there are no points of intersection with the abscissa axis.
Taking into account the conducted research, it is possible to build a graph of the function
Schematic graph of a function 
shown in fig. 3.10.
Rice. 3.10.
3.4.2.5 Asymptotes of the graph of a function
Definition. Asymptote the graph of the function is called a straight line, which has the property that the distance from the point () to this straight line tends to 0 with an unlimited removal of the graph point from the origin.
