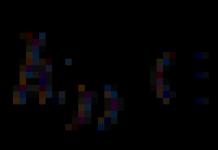U slučaju poprečnog savijanja u dijelovima grede ne nastaje samo moment savijanja, već i poprečna sila. Posljedično, u ovom slučaju nastaju ne samo normalni, već i tangencijalni naponi u poprečnim presjecima grede.
Budući da su tangencijalni naponi općenito neravnomjerno raspoređeni po presjeku, tada, strogo govoreći, presjeci grede ne ostaju ravni tijekom poprečnog savijanja. Međutim, na (gdje h- visina poprečnog presjeka, l je duljina grede) pokazuje se da ta izobličenja ne utječu osjetno na rad grede pri savijanju. U ovom slučaju, hipoteza o ravnim presjecima također je prihvatljiva s dovoljnom točnošću u slučaju čistog savijanja. Stoga se ista formula (6.4) koristi za izračunavanje normalnih naprezanja s.
Razmotrite izvođenje formula za izračun posmičnih naprezanja. Izdvojimo iz šipke koja doživljava poprečno savijanje element s dužinom dx(Sl. 6.6 A).

| A |
| b |
| V |
| G |
| A * |

Uzdužni horizontalni presjek nacrtan na daljinu z od neutralne osi, element dijelimo na dva dijela (sl. 6.6 V) i razmotrite ravnotežu gornjeg dijela, koji ima bazu širine b. Istodobno, uzimajući u obzir zakon uparivanja tangencijalnih naprezanja, dobivamo da su tangencijalni naponi u presjeku jednaki tangencijalnim naprezanjima koja se javljaju u uzdužnim presjecima (slika 6.6 b). Uzimajući u obzir ovu okolnost i iz pretpostavke da posmična naprezanja po području b× dx ravnomjerno raspoređeni, koristeći uvjet åx = 0, dobivamo:
N * - N * - dN* + t× b× dx = 0 ,
 . (6.5)
. (6.5)
Gdje N* - rezultanta normalnih sila s× dA u lijevom presjeku
element dx unutar područja A* (Sl. 6.6 G):
 . (6.6)
. (6.6)
Uzimajući u obzir (6.4), zadnji izraz se može prikazati kao
 , (6.7)
, (6.7)
Gdje  - statički moment dijela presjeka koji se nalazi iznad koordinate g(na sl. 6.6 b ovo područje je zasjenjeno).
- statički moment dijela presjeka koji se nalazi iznad koordinate g(na sl. 6.6 b ovo područje je zasjenjeno).
Stoga se (6.7) može prepisati kao  , gdje
, gdje
 . (6.8)
. (6.8)
Kao rezultat zajedničkog razmatranja (6.7) i (6.8), dobivamo
 ,
,
ili konačno
 . (6.9)
. (6.9)
Formula (6.9) je nazvana po ruskom znanstveniku D.I. Zhuravsky.
Za proučavanje stanja naprezanja u proizvoljnoj točki grede koja doživljava poprečno savijanje, odabiremo elementarnu prizmu iz sastava grede oko točke koja se proučava (slika 6.6). G), tako da je okomita platforma dio presjeka grede, a nagnuta platforma čini proizvoljan kut a u odnosu na horizont. Prihvaćamo da odabrani element ima sljedeće dimenzije duž koordinatnih osi: duž uzdužne osi - dx, tj. duž osi x; po okomitoj osi - dz, tj. duž osi z; duž osi g- jednaka širini grede.
Budući da okomito područje odabranog elementa pripada poprečnom presjeku grede koja doživljava poprečno savijanje, normalna naprezanja s na ovom mjestu određuju se formulom (6.4), a posmična naprezanja t- prema formuli D.I. Žuravski (6,9). Uzimajući u obzir zakon sparivanja posmičnih naprezanja, lako je ustanoviti da su posmična naprezanja na horizontalnoj platformi također jednaka t. Normalna naprezanja na ovom mjestu jednaka su nuli, prema hipotezi nama već poznate teorije savijanja da uzdužni slojevi ne vrše pritisak jedni na druge.
Označimo vrijednosti normalnih i posmičnih naprezanja na nagnutom području kroz s a I ta, odnosno. Uzimajući područje nagiba dA, za vertikalne i horizontalne platforme ćemo imati dA grijeh a i dA cos a odnosno.
Sastavljanje jednadžbi ravnoteže za elementarnu prizmu (sl. 6.6 G), dobivamo:

 ,
,
odakle ćemo imati:
Stoga konačni izrazi za naprezanja na nagnutoj platformi imaju oblik:

Odredimo orijentaciju mjesta, tj. vrijednost a = a 0 , pri kojoj napon s a poprima ekstremnu vrijednost. Prema pravilu za određivanje ekstrema funkcija iz matematičke analize uzimamo derivaciju funkcije s a iz a i izjednačavamo je s nulom:
 .
.
Pretpostavljajući a = a 0, dobivamo:  .
.
Odakle ćemo konačno imati:  .
.
Prema posljednjem izrazu, ekstremna naprezanja nastaju na dva međusobno okomita područja, tzv glavni, i sami stresovi - glavna naprezanja.
Uspoređujući izraze t a i  , imamo:
, imamo:  , odakle slijedi da su tangencijalni naponi na glavnim područjima uvijek jednaki nuli.
, odakle slijedi da su tangencijalni naponi na glavnim područjima uvijek jednaki nuli.
Zaključno, uzimajući u obzir dobro poznate trigonometrijske identitete:

i formule  , određujemo glavna naprezanja, izražavajući iz u smislu s i t.
, određujemo glavna naprezanja, izražavajući iz u smislu s i t.
Vidjeli smo da kod čistog savijanja u poprečnim presjecima štapa nastaju samo normalna naprezanja. Odgovarajuće unutarnje sile svode se na moment savijanja u presjeku. U slučaju poprečnog savijanja u presjeku štapa ne nastaje samo moment savijanja, već i poprečna sila, koja je rezultanta elementarno raspodijeljenih sila koje leže u ravnini presjeka (slika 4.23). Posljedično, u ovom slučaju, u poprečnim presjecima nastaju ne samo normalni, već i posmični naponi.

Pojava tangencijalnih naprezanja praćena je pojavom kutnih deformacija. Stoga, pored osnovnih pomaka svojstvenih čistom savijanju, svako elementarno područje presjeka dobiva neke dodatne kutne pomake zbog smicanja. Posmična naprezanja su neravnomjerno raspoređena po presjeku, pa će i kutni pomaci biti neravnomjerno raspoređeni. To znači da kod poprečnog savijanja, za razliku od čistog izpb a, presjeci ne ostaju ravni. Na sl. 4.24 prikazuje tipičnu sliku zakrivljenosti poprečnih presjeka.


Međutim, iskrivljenje ravnine presjeka ne utječe značajno na vrijednost normalnih naprezanja. Konkretno, ako se poprečna sila ne mijenja po duljini štapa, formule (4.6) i (4.8), izvedene za slučaj čistog savijanja, dat će potpuno točne rezultate u slučaju poprečnog savijanja. Doista, kada se zakrivljenost svih sekcija događa na isti način (slika 4.25). Dakle, uz međusobnu rotaciju dvaju susjednih odsječaka, produljenje uzdužnog vlakna AB bit će isto, bez obzira da li odsjek ostaje ravan ili ne.
S poprečnom silom koja varira duž osi štapa, formule za čisto savijanje daju određenu pogrešku za a. Jednostavnom analizom može se pokazati da je ta pogreška reda veličine u usporedbi s jedinicom, gdje je veličina presjeka u ravnini savijanja; - duljina šipke. Prema definiciji danoj u § B2, karakteristična značajka štapa je da su dimenzije njegovog presjeka mnogo manje od njegove duljine. Posljedično, omjer je relativno malen i navedena pogreška se pokazuje odgovarajuće malom.
Sve navedeno daje razlog za prihvaćanje hipoteze ravnih presjeka. Nadalje ćemo pretpostaviti da skup točaka koje tvore ravninu presjeka prije savijanja također tvori ravninu rotiranu u prostoru nakon savijanja. Ova pretpostavka je prihvatljiva do te mjere da se kutne deformacije 7 u presjeku mogu smatrati znatno manjim od kutnih pomaka zbog promjene zakrivljenosti.
Značajka poprečnog savijanja također je prisutnost normalnih naprezanja koja nastaju u uzdužnim presjecima grede, tj. naprezanja između slojeva. Ova naprezanja nastaju samo s promjenjivom poprečnom silom i vrlo su mala.
Dakle, u okviru navedenih pretpostavki, formule (4.6) i (4.8), izvedene za određivanje normalnih naprezanja, vrijede ne samo za čisto savijanje, već i za poprečno savijanje. Jednako je primjenjiva formula (4.5) koja daje ovisnost zakrivljenosti štapa o momentu savijanja.
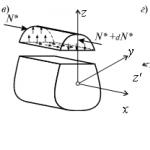
Sada približno odredimo tangencijalna naprezanja pri poprečnom savijanju. Najlakši način za izračunavanje ovih naprezanja je preko uparenih posmičnih naprezanja koja nastaju u uzdužnim presjecima štapa. Odaberimo element duljine iz grede (slika 4.26, a). U slučaju poprečnog savijanja, momenti koji nastaju u lijevom i desnom dijelu elementa nisu isti i razlikuju se u uzdužnom vodoravnom presjeku nacrtanom na udaljenosti y od neutralnog sloja (sl. 4.26, b), dijelimo element na dva dijela i razmotrite uvjete ravnoteže gornjeg dijela. Rezultanta normalnih sila u lijevom dijelu unutar osjenčanog područja je, očito,

ili, prema formuli (4.6),


gdje, za razliku od y, označava trenutnu ordinatu mjesta (vidi sl. 4.26, b). Rezultirajući integral je statički moment oko x-osi dijela područja koji se nalazi iznad uzdužnog presjeka (iznad razine Označimo ovaj statički moment sa Tada

U desnom dijelu, normalna sila će biti drugačija:

Razlika između tih sila

mora biti uravnotežen tangencijalnim silama koje nastaju u uzdužnom presjeku elementa (vidi sl. 4.26, b i c).
Kao prvu aproksimaciju pretpostavljamo da su posmična naprezanja ravnomjerno raspoređena po širini presjeka. Zatim
![]()
Rezultirajuća formula naziva se formula Žuravskog, prema ruskom znanstveniku iz prošlog stoljeća, koji je prvi proveo opću studiju posmičnih naprezanja pri poprečnom savijanju.
Izraz (4.12) omogućuje izračunavanje posmičnih naprezanja koja nastaju u uzdužnim presjecima šipke. Naprezanja nastala u poprečnim presjecima štapa jednaka su im, kao paru. Ovisnost o y u presjeku određena je statičkim momentom 5. Pri približavanju gornjem rubu presjeka, površina njegovog zasjenjenog dijela (vidi sl. 4.26, b) smanjuje se na nulu. Ovdje, dakle, kada se približi donjem rubu, osjenčani dio pokriva cijeli dio. Budući da je os središnja, i ovdje su posmična naprezanja, kako slijedi iz formule (4.12), u gornjoj i donjoj točki presjeka jednaka nuli.

Za pravokutnu šipku sa stranama i (slika 4.27, a) imamo
Stoga,

a dijagram tangencijalnih naprezanja po visini presjeka prikazuje se kvadratnom parabolom. Najveći stres javlja se kod
![]()
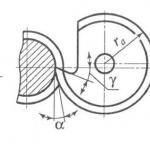
Za kružni štap (sl. 4.27, b), jednostavnom operacijom integracije, možete pronaći

Osim,
![]()
![]()
Za štap koji ima presjek u obliku trokuta s bazom c i visinom (slika 4.27, c),

Maksimalno naprezanje javlja se na udaljenosti od neutralne osi:
![]()
Posljednja dva primjera jasno pokazuju približnu prirodu izvedenih operacija. To se vidi iz činjenice da u presjeku posmična naprezanja imaju komponente ne samo duž y osi, već i duž x osi. Doista, pretpostavimo, kao što je učinjeno gore, da je za točke A koje se nalaze u blizini konture presjeka (slika 4.28), smično naprezanje usmjereno duž osi y. Rastavimo vektor na dvije komponente - po normali na konturu i po tangenti.Prema uvjetima opterećenja vanjska površina štapa je oslobođena tangencijalnih sila. Stoga nema naponskih parova. Dakle, dok je ukupni smični napon u blizini konture usmjeren tangencijalno na konturu, a pretpostavka da je usmjeren duž osi y pokazuje se netočnom. Tako se detektira prisutnost komponenata duž x-osi. Za određivanje ovih komponenti treba pribjeći složenijim metodama od


pregledan ranije. Korištenjem metoda teorije elastičnosti može se pokazati da u većini slučajeva komponente duž x-osi imaju znatno manju ulogu nego duž y-osi.
Iz gore razmotrenih primjera možemo općenito zaključiti da se zona maksimalnih posmičnih naprezanja nalazi približno u sredini visine presjeka, a za presjeke bez tankih stijenki ima vrijednost reda
Moguće je usporediti apsolutne vrijednosti maksimalnih normalnih i maksimalnih posmičnih naprezanja koja nastaju u poprečnim presjecima šipke. Na primjer, za pravokutnu konzolu (sl. 4.29) imamo

To znači da su maksimalni posmični naponi u presjeku povezani s najvećim normalnim naprezanjima približno kao što je visina presjeka u odnosu na duljinu štapa, tj. smična naprezanja su znatno manja od normalnih. Navedena procjena, uz nekoliko iznimaka, sačuvana je za sve netankostijene šipke. Što se tiče šipki s tankim stijenkama, to je posebna tema.
Zbog malenosti τmax, proračun čvrstoće pri poprečnom savijanju izvodi se samo za normalna naprezanja, kao kod čistog savijanja. Posmična naprezanja se ne uzimaju u obzir. To je tim prirodnije što u točkama presjeka koje su najudaljenije od neutralne crte, t.j. kod najopasnijih su posmična naprezanja u presjeku jednaka nuli.
S obzirom na kvalitativnu stranu pojave, treba imati na umu da posmična naprezanja u poprečnim presjecima i njihova uparena naprezanja u uzdužnim presjecima, unatoč svojoj malenosti, mogu u nekim slučajevima značajno utjecati na ocjenu čvrstoće štapa. Na primjer, kod poprečnog savijanja kratke drvene grede moguće je uništenje ne duž poprečnog presjeka u ugradnji, već smicanje duž uzdužne ravnine blizu neutralnog sloja, tj. gdje su posmični naponi maksimalni (slika 4.30).

Posmična naprezanja u uzdužnim presjecima izraz su postojeće veze između slojeva štapa pri poprečnom savijanju. Ako se ta veza u nekim slojevima prekine, priroda savijanja štapa se mijenja. Na primjer, u šipki sastavljenoj od listova (slika 4.31, a), svaki list se savija neovisno u nedostatku sila trenja. Vanjska sila na lim jednaka je a najveći normalni napon u presjeku lima jednak je
U slučaju poprečnog savijanja u presjecima grede ne javlja se samo moment savijanja, već i poprečna sila. Posljedično, u ovom slučaju nastaju ne samo normalni, već i tangencijalni naponi u poprečnim presjecima grede.
Budući da su tangencijalni naponi općenito neravnomjerno raspoređeni po presjeku, tada, strogo govoreći, presjeci grede ne ostaju ravni tijekom poprečnog savijanja. Međutim, na (gdje h- visina poprečnog presjeka, l- duljina grede) pokazuje se da ta izobličenja ne utječu osjetno na rad grede pri savijanju. U ovom slučaju, hipoteza o ravnim presjecima također je prihvatljiva s dovoljnom točnošću u slučaju čistog savijanja. Stoga se ista formula (5) koristi za izračunavanje normalnih naprezanja.
Razmotrite izvođenje formula za izračun posmičnih naprezanja. Izdvojimo iz šipke koja doživljava poprečno savijanje element s duljinom (Sl. 6.28, A).
Riža. 6.28
S uzdužnim horizontalnim presjekom nacrtanim na udaljenosti y od neutralne osi, dijelimo element na dva dijela (sl. 6.28, V) i razmotrite ravnotežu gornjeg dijela, koji ima bazu širine b. Istodobno, uzimajući u obzir zakon uparivanja tangencijalnih naprezanja, dobivamo da su tangencijalni naponi u presjeku jednaki tangencijalnim naprezanjima koja nastaju u uzdužnim presjecima (sl. 6.28, b). Uzimajući u obzir ovu okolnost i iz pretpostavke da su posmična naprezanja ravnomjerno raspoređena po površini, korištenjem uvjeta dobivamo:
gdje je rezultanta normalnih sila u lijevom presjeku elementa unutar osjenčanog područja:
Uzimajući u obzir (5), zadnji izraz se može prikazati kao
gdje je statički moment dijela poprečnog presjeka koji se nalazi iznad y koordinate (na slici 6.28, b ovo područje je zasjenjeno). Stoga se (15) može prepisati kao
Kao rezultat zajedničkog razmatranja (13) i (16), dobivamo
ili konačno
Dobivena formula (17) nazvana je po ruskom znanstveniku DI. Zhuravsky.
Uvjeti čvrstoće za posmična naprezanja:
gdje je najveća vrijednost poprečne sile u presjeku; - dopušteni smični napon, obično je jednak polovici.
Za proučavanje stanja naprezanja u proizvoljnoj točki grede koja doživljava poprečno savijanje, odabiremo elementarnu prizmu iz sastava grede oko točke koja se proučava (slika 6.28, G), tako da je okomita platforma dio presjeka grede, a nagnuta platforma čini proizvoljan kut u odnosu na horizont. Prihvaćamo da odabrani element ima sljedeće dimenzije duž koordinatnih osi: duž uzdužne osi - dz, tj. duž osi z; po okomitoj osi - dy, tj. duž osi na; duž osi x- jednaka širini grede.
Budući da okomito područje odabranog elementa pripada poprečnom presjeku grede koja doživljava poprečno savijanje, normalna naprezanja na ovom području određena su formulom (5), a posmična naprezanja određena su D.I. Žuravski (17). Uzimajući u obzir zakon sparivanja posmičnih naprezanja, lako je ustanoviti da su posmična naprezanja na horizontalnoj platformi također jednaka. Normalna naprezanja na ovom mjestu jednaka su nuli, prema hipotezi nama već poznate teorije savijanja da uzdužni slojevi ne vrše pritisak jedni na druge.
Označimo vrijednosti normalnih i tangencijalnih naprezanja na nagnutom području kroz i , respektivno. Uzimajući područje nagnute platforme, za okomite i vodoravne platforme imat ćemo i , respektivno.
Sastavljanje jednadžbi ravnoteže za elementarnu presječenu prizmu (Sl. 6.28, G), dobivamo:
odakle ćemo imati:
Posljedično, konačni izrazi za naprezanja na nagnutoj platformi imaju oblik:
Odredimo orijentaciju mjesta, tj. vrijednost pri kojoj napon doseže svoju ekstremnu vrijednost. Prema pravilu za određivanje ekstrema funkcija iz matematičke analize uzimamo derivaciju funkcije iz i izjednačavamo je s nulom:
Pod pretpostavkom da dobijemo:
Odakle ćemo konačno imati:
Prema posljednjem izrazu, ekstremna naprezanja nastaju na dva međusobno okomita područja, tzv glavni , i sami stresovi - glavna naprezanja.
Uspoređujući izraze i , imamo:
odakle slijedi da su tangencijalni naponi na glavnim područjima uvijek jednaki nuli.
Zaključno, uzimajući u obzir dobro poznate trigonometrijske identitete:
i formule,
određujemo glavna naprezanja, izražavajući kroz i:
Iz grede smo izrezali u blizini određene točke elementarni paralelopiped 1-2-3-4 (sl. 45.7, a) čije su bočne strane 1-2 i 3-4 smještene u poprečnim presjecima grede, a bočna lica 2-3 i 1-4 su paralelni neutralni sloj. Duljina kutije (u smjeru okomitom na crtež) jednaka je širini grede. Naponi koji djeluju na stranama paralelepipeda razmatraju se u § 7.7 i 8.7; prikazani su na sl. 45.7b. Na plohama 1-2 i 3-4 djeluju normalna naprezanja a i tangencijalna naprezanja, a na plohama 2-3 i 1-4 samo tangencijalna naprezanja. Smjerovi ovih napona, prikazani na si. 45.7, b, odgovaraju slučaju kada pozitivni moment savijanja i poprečna sila djeluju u presjecima razmatranog presjeka grede.

Vrijednosti naprezanja određene su formulama (17.7) i (28.7).
Prednja i stražnja strana elementarnog paralelopipeda podudaraju se s bočnim površinama grede, slobodnim od opterećenja, pa su naprezanja na tim stranama jednaka nuli. Prema tome, paralelopiped je u ravnom stanju naprezanja.
U područjima nagnutim pod različitim kutovima prema bočnim stranama elementarnog paralelopipeda djeluju normalni i tangencijalni naponi, čije se vrijednosti mogu odrediti formulama (6.3) i (7.3). Postoje dva međusobno okomita područja duž kojih su posmična naprezanja jednaka nuli. Ta se područja, kao što je poznato, nazivaju glavnim područjima, a normalna naprezanja koja u njima djeluju nazivaju se glavnim naprezanjima (vidi § 3.3). U područjima koja su nagnuta pod kutom od 45° u odnosu na glavna područja, djeluju ekstremna posmična naprezanja; ta se područja nazivaju područjima smicanja (vidi § 4.3).
Određivanje glavnih normalnih i ekstremnih posmičnih naprezanja u općem slučaju ravnog stanja naprezanja vrši se, kao što je poznato, prema formulama (12.3) i (15.3):

Zamijenite vrijednosti u ovim formulama

Ovdje - normalni i tangencijalni naponi u točki koja se razmatra, djeluju na mjestu, podudaraju se s presjekom grede i određuju se formulama (17.7) i (28.7).
Iz formule (32.7) se vidi da je napon otax uvijek pozitivan, a uvijek negativan. Stoga, u skladu s pravilom, prema kojem treba označiti napon otaks i označiti naprezanje Srednje glavno naprezanje javlja se u glavnim područjima paralelnim s ravninom crteža (sl. 45.7).
Kut nagiba glavnih platformi prema bočnim stranama elementarnog paralelopipeda može se odrediti metodom navedenom u § 3.3.
Vrijednosti glavnih normalnih i ekstremnih posmičnih naprezanja i položaji mjesta na kojima djeluju također se mogu odrediti pomoću Mohrovog kruga (vidi § 5.3).
Razmotrimo sada detaljnije stanje naprezanja u točkama pravokutnog presjeka grede. Pretpostavimo da su moment savijanja M i poprečna sila Q u ovom presjeku pozitivni.
U presjeku, u točkama koje su najudaljenije od neutralne osi, posmična naprezanja su nula, a normalna naprezanja a su jednaka (u točki a na slici 46.7, a) i (u točki a na slici 46.7, a). Dakle, za svaku od ovih točaka jedno od glavnih područja podudara se s presjekom grede, a druga dva su okomita na presjek (normalni naponi u njima jednaki su nuli). U tim točkama postoji jednoosno stanje naprezanja.
Na sl. 46.7, ali prikazani su elementarni paralelopipedi čije su bočne strane paralelne s dvije glavne platforme; treća glavna platforma je paralelna s ravninom crteža. Ekstremna posmična naprezanja u točkama a do a određena su formulom
U presjeku u točkama koje se nalaze na neutralnoj osi (točka b na slici 46.7, a), normalni napon o je nula, a napon smicanja. U tim točkama stanje naprezanja je čisto smicanje s ekstremnim posmičnim naprezanjima
Dvije glavne platforme na svakoj od ovih točaka nagnute su pod kutom od ± 45 ° u odnosu na os grede (vidi sl. 46.7, a), a glavni naponi u njima.
Treća glavna platforma je paralelna s ravninom crteža; naponi u njemu jednaki su nuli.
U presjeku u ostalim točkama naprezanja a i različita su od nule. Na različitim udaljenostima od neutralne osi, omjeri između vrijednosti a i su različiti, pa su stoga kutovi nagiba glavnih platformi prema osi grede također različiti. U svakoj od ovih točaka glavna naprezanja koja nisu jednaka nuli imaju suprotne predznake, tj. stanje naprezanja je i napetost i pritisak u dva međusobno okomita smjera.

Određivanjem vrijednosti glavnih naprezanja za niz točaka koje se nalaze u istom presjeku grede na različitim udaljenostima od neutralne osi, tada je moguće konstruirati dijagrame glavnih naprezanja iz tih vrijednosti. Ovi dijagrami karakteriziraju promjenu glavnih naprezanja po visini grede.
Slično tome, moguće je izračunati vrijednosti ekstremnih posmičnih naprezanja i izgraditi dijagrame tih naprezanja. Na sl. 46.7, b za pravokutni presjek grede, u kojem djeluju pozitivni moment savijanja M i poprečna sila Q, dijagrami naprezanja koji se pojavljuju u područjima koja se podudaraju s presjekom, dijagrami glavnih naprezanja i ekstremnih smičnih naprezanja.
Odredimo za neku točku grede smjer jednog od glavnih naprezanja, a zatim uzmimo drugu točku u tom smjeru, dovoljno blizu prvoj. Nakon što smo pronašli smjer glavnog naprezanja za drugu točku, na sličan način označavamo treću točku itd.
Spajanjem tako pronađenih točaka dobivamo tzv. putanju glavnih naprezanja. Dvije takve putanje prolaze kroz svaku točku, okomite jedna na drugu; jedan od njih predstavlja putanju glavnih vlačnih naprezanja, a drugi - glavnih tlačnih. Putanje glavnih vlačnih naprezanja čine jednu obitelj krivulja, a putanje glavnih tlačnih naprezanja drugu obitelj. Tangenta na putanju u bilo kojoj točki daje smjer odgovarajućeg (vlačnog ili tlačnog) glavnog naprezanja u toj točki.

Na sl. 47.7 prikazuje dio pročelja grede s primijenjenim putanjama glavnih naprezanja. Sve one sijeku os grede pod kutovima od ±45° i približavaju se gornjoj i donjoj plohi grede pod kutovima od 0 i 90°; to odgovara smjerovima glavnih područja (i glavnih naprezanja) prikazanih na sl. 46.7, a.

Uzdužna sila 
![]()
![]()
Pri izvođenju proračunskih formula za određivanje normalnog naprezanja uzima se sljedeća pretpostavka: uzdužna os ne mijenja svoju duljinu pri savijanju, uzdužne linije se savijaju duž polumjera. Obrisi poprečnih presjeka su ravni prije opterećenja i ostaju ravni nakon opterećenja; konturne linije presjeka posvuda su okomite na uzdužnu os.
Postoji sloj koji ne mijenja svoju duljinu kada se savija - naziva se neutralni sloj.
Pri križanju neutralnog sloja poprečnim presjekom dobivamo neutralnu liniju.
S ravnim zavojem, neutralni sloj ispada da je okomit na ravninu sile i, prema tome, neutralna linija je okomita na liniju sile presjeka.
Odaberimo sada gredni element duljine dx s dva presjeka.

Relativna deformacija vlakana jednaka je razlici duljina vlakana ![]()
![]()
Razmotrimo vlakno a 0 b 0 koje pripada normalnom sloju, njegova duljina je jednaka segmentu dx, nakon deformacije, segment se pretvara u luk a 0 ’b 0 ’=
Vlakno neutralnog sloja ne mijenja svoju duljinu tijekom deformacije => dx=, zamjenjujući ovaj izraz u formulu za relativnu deformaciju
prema Hookeovom zakonu, uspoređujući ove izraze =>, ovdje je y udaljenost od neutralne linije do točke u kojoj je ovaj napon određen, zamjenjujući ovaj izraz u izraz za trenutak: ![]()


![]()
U slučajevima poprečnog savijanja, proračun normalnih naprezanja provodi se prema istoj formuli kao i za čisto savijanje, budući da je razlika u rezultatima praktički jednaka nuli, a rezultirajuće posmično naprezanje može doseći velike vrijednosti, a određuje se tijekom savijanja pomoću formule Žuravskog. 
Određivanje posmičnog naprezanja pri poprečnom savijanju
S poprečnim presjekom, poprečnim silama Q i momentima savijanja nastaje ne samo normalno, već i posmično naprezanje
Razmotrite izvođenje formule za određivanje posmičnih naprezanja na gredi s poprečnim presjekom
![]()

Ove pretpostavke vrijede ako je širina presjeka b mnogo manja od h.
Dio grednog elementa označavamo povlačenjem horizontalne ravnine mm na udaljenosti y od neutralne linije
Na plohama A 1 A 2 m 2 m 1, C 1 C 2 n 2 n 1 i A 1 A 2 C 2 C 1 nema naprezanja jer ta su lica dio vanjske površine grede.
Potrebno je izračunati rezultantu normalnih naprezanja raspoređenih po površini A 1 C 1 m 1 n 1 na elementarnu površinu dF=bd, povučenu paralelno s osi z, na udaljenosti od nje djeluje normalna aksijalna sila. ![]()
![]()

Statistički moment površine zatvorene između razine Y i vanjskog ruba grede
![]()
Slično, na površini A 2 C 2 n 2 m 2, rezultanta normalnih naprezanja bit će jednaka: ![]()
vrijednost statičkog momenta odsječene ravnine bit će ista kao u prethodnom izrazu.
U čeonici n 1 n 2 m 1 m 2 djeluje normalno naprezanje, budući da se vlakna pri poprečnom savijanju pritišću jedno na drugo, ali se ta naprezanja zanemaruju kao beznačajna za proračun čvrstoće.
Osim toga, prema zakonu sparivanja posmičnih naprezanja, posmična naprezanja nastaju u okomitom smjeru duž ZPKN
Jer duljina lica n 1 n 2 m 1 m 2 je mala, tj. jednak dx, možemo pretpostaviti da su ravnomjerno raspoređeni po ovoj površini.
![]()
Uvjet ravnoteže paralelopipeda: a 1 a 2 c 2 c 1 n 1 n 2 m 2 m 1

![]()
Ako dobivenu jednakost podijelimo s bdx, tada je: ![]() - formula Žuravskog,
- formula Žuravskog,
Što vam omogućuje određivanje količine posmičnih naprezanja tijekom poprečnog savijanja na bilo kojoj razini poprečnog presjeka
![]()