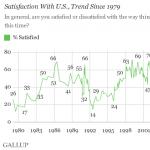
10x − 5y − 3z = − 9,
6 x + 4 y − 5 z = − 1.3 x − 4 y − 6 z = − 23.
Let's equalize the coefficients for x in the first and second equations; to do this, multiply both sides of the first equation by 6, and of the second equation by 10, we get:
60x − 30 y − 18z = − 54.60x + 40 y − 50z = − 10.
We subtract the first equation from the second equation of the resulting system.
Therefore, we get: 70 y − 32 z = 44, 35 y − 16 z = 22.
From the second equation of the original system we subtract the third equation multiplied by 2, we get: 4 y + 8 y − 5 z + 12 z = − 1 + 46,
12 y + 7z = 45.
Now we solve a new system of equations:
35y − 16z = 22.12y + 7z = 45.
To the first equation of the new system, multiplied by 7, we add the second equation, multiplied by 16, we get:
35 7 y + 12 16y = 22 7 + 45 16,
Now we substitute y = 2, z = 3 into the first equation of the original system
topics, we get: 10x − 5 2 − 3 3 = − 9, 10x − 10 − 9 = − 9, 10x = 10, x = 1.
Answer: (1; 2;3). ▲
§ 3. Solution of systems with parameters and with modules
ax + 4 y = 2 a,
Consider the system of equations
x + ay = a.

2010-2011 academic year year., No. 3, 8th grade. Mathematics. Systems of equations.
There are actually three variables in this system, namely: a, x, y. x and y are considered unknown, a is called a parameter. It is required to find solutions (x, y) of this system for each value of the parameter a.
Let us show how such systems solve. Let us express the variable x from the second equation of the system: x = a − ay. We substitute this value for x into the first equation of the system, we get:
a (a − ay) + 4 y = 2 a,
(2 − a )(2 + a ) y = a (2 − a ) .
If a = 2, then we get the equation 0 y = 0. This equation is satisfied by any number y, and then x = 2 − 2 y, i.e., for a = 2, the pair of numbers (2 − 2 y; y) is a solution to the system . Since y can be
any number, then the system with a = 2 has infinitely many solutions.
If a = − 2, then we get the equation 0 y = 8. This equation has no solution.
If now a ≠ ± 2, |
then y = |
a (2 − a) |
|||||||
(2 − a )(2 + a ) |
2+a |
||||||||
x = a − ay = a − |
|||||||||
2+a |
|||||||||
Answer: For a = 2, the system has infinitely many solutions of the form (2 − 2 y; y), where y is any number;
for a = − 2 the system has no solutions; |
||||||
for a ≠ ± 2, the system has a unique solution |
. ▲ |
|||||
2+a |
2+a |
We solved this system and established for what values of the parameter a the system has one solution, when it has infinitely many solutions, and for what values of the parameter a it has no solutions.
Example 1: Solve the system of equations
© 2010, FZFTSH at MIPT. Compiled by: Yakovleva Tamara Kharitonovna

2010-2011 academic year year., No. 3, 8th grade. Mathematics. Systems of equations.
−3 |
y − 1 |
|||||||||||
3x − 2 y = 5. |
||||||||||||
From the second equation of the system we express x through y, we get |
||||||||||||
2 y + 5 |
we substitute this value for x into the first equation of the system |
|||||||||||
topics, we get: |
2y + 5 |
−3 |
y − 1 |
−3 |
−1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5 = 0 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Expression |
y = − |
y > − |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
; If |
−5 |
= −y |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Expression y − 1 = 0, |
if y = 1. If |
y > 1, then |
y − 1 |
Y − 1, and es- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
whether y< 1, то |
y − 1 |
1 − y . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If y ≥ 1, then |
y − 1 |
Y−1 and |
we get the equation: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
−3(y |
− 1) = 3, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
−3 y |
3, − |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(2 2 + |
5 ) = 3. The number 2 > 1, so the pair (3;2) is re- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
changing the system. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Let it now |
5 ≤ y<1, |
y − 1 |
− y ; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
finding |
we get |
equation |
3y−3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4 y + 10 |
3 y = 6, |
13 y = 8 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
© 2010, FZFTSH at MIPT. Compiled by: Yakovleva Tamara Kharitonovna

2010-2011 academic year year., No. 3, 8th grade. Mathematics. Systems of equations.
(2 y + 5) = |
||||||||||||||||||||||||||||||
But less than |
so a couple of numbers |
|||||||||||||||||||||||||||||
is a solution to the system. |
||||||||||||||||||||||||||||||
y< − |
then we get the equation: |
3y−3 |
||||||||||||||||||||||||||||
4 y − |
3y = 6, |
5 y = |
28, y = 28. |
meaning |
||||||||||||||||||||||||||
so there are no solutions. |
||||||||||||||||||||||||||||||
Thus, the system has two solutions (3;2) and 13 27 ; 13 8 . ▲
§ 4. Solving problems using systems of equations
Example 1. A car travels from a city to a village in 2.5 hours. If he increases his speed by 20 km/h, then in 2 hours he will cover a distance of 15 km greater than the distance from the city to the village. Find this distance.
Let us denote by S the distance between the city and the village and by V the speed of the car. Then to find S we obtain a system of two equations
2.5V = S,
(V + 20) 2 = S + 15.
© 2010, FZFTSH at MIPT. Compiled by: Yakovleva Tamara Kharitonovna

2010-2011 academic year year., No. 3, 8th grade. Mathematics. Systems of equations.
into the second equation: |
S + 20 2 |
S +15, |
S = 25, |
S = 125. |
||
Answer: 125 km. ▲
Example 2. The sum of the digits of a two-digit number is 15. If these digits are swapped, you get a number that is 27 more than the original. Find these numbers.
Let the given number ab, i.e. the number of tens is a, and the number of ones is b. From the first condition of the problem we have: a + b = 15. If we subtract the number ab from the number ba, we get 27, hence we get the second equation: 10 b + a − (10 a + b) = 27. x
2010-2011 academic year year., No. 3, 8th grade. Mathematics. Systems of equations.
Let's multiply both sides of the equation by 20, we get: x + 8 y = 840. To find x and y we get a system of equations
Answer: 40 t, 100 t. ▲
Example 4. A computer operator, working with a student, processes a task in 2 hours 24 minutes. If the operator works for 2 hours, and the student for 1 hour, then
children completed 2 3 of the entire work. How long will it take to operate
ru and the student separately to process the task?
Let's denote all work by 1, operator productivity by x, and student productivity by y. We take into account that
2 hours 24 minutes = 2 5 2 hours = 12 5 hours.
From the first condition of the problem it follows that (x+y) 12 5 = 1. From the second condition of the problem it follows that 2 x + y = 2 3. We received a system of equations
(x+y) |
|||||||||||||||||||||||||||
2 x + y = |
|||||||||||||||||||||||||||
We solve this system using the substitution method: |
|||||||||||||||||||||||||||
− 2 x ; |
|||||||||||||||||||||||||||
−2x |
−x |
− 1; |
|||||||||||||||||||||||||
; x = |
; y = |
||||||||||||||||||||||||||
© 2010, FZFTSH at MIPT. Compiled by: Yakovleva Tamara Kharitonovna
Back Forward
Attention! Slide previews are for informational purposes only and may not represent all of the presentation's features. If you are interested in this work, please download the full version.
Purpose of the lesson. Solving equations with parameters and modules, applying the properties of functions in unexpected situations and mastering geometric techniques for solving problems. Non-standard equations.
Tasks:
- Educational: teach how to solve some types of equations using modules and parameters;
- Developmental: develop a culture of thought, a culture of speech and the ability to work with a notebook and blackboard.
- Educational: cultivate independence and the ability to overcome difficulties.
Equipment: visual material for oral calculation and explanation of a new topic. Interactive whiteboard, multimedia lesson equipment.
Lesson structure:
- Repetition of studied material (oral counting).
- Learning new material.
- Consolidation of the studied material.
- Lesson summary.
- Homework.
PROGRESS OF THE LESSON
1. Repetition of the most important theoretical material on topics: “Equations containing a modulus”, “Solving equations with parameters”
1) “Equations containing a modulus”
The absolute value or modulus of a number a is the number a, If a> 0, number – a, If a < 0, нуль, если a= 0. Or
From the definition it follows that | a | >
0 and | a | >
a for everyone a€ R .
Inequality | x | < a, (If a> 0) is equivalent to a double inequality – a <
X < a.
Inequality | x | < a, (If a < 0)
не имеет смысла, так как | х | >0.
Inequality | x | > a, (If a> 0) is equivalent to two inequalities
Inequality | x | > a, (If a < 0)
справедливо для любого X€ R
2) “Solving equations with parameters”
To solve an equation with parameters means to indicate at what values of the parameters solutions exist and what they are.
a) determine the set of acceptable values of the unknown and parameters;
b) for each admissible system of parameter values, find the corresponding sets of solutions to the equation.
2. Oral exercises
1. Solve the equation | x– 2 | = 5; Answer: 7; – 3
| x– 2 | = – 5; Answer: no solution
| x– 2 | = x + 5; Answer: no solution; 1.5
| x– 2 | = | x+ 5 |; Answer: no solution; – 1.5; there is no solution; – 1.5;
2. Solve the equation: | x+ 3 | + | y– 2 | = 4;
Let's consider four cases
| { | x + 3 > 0 | { | x > – 3 |
| y – 2 > 0 | y > 2 | ||
| x + 3 + y – 2 = 4 | y = – x + 3 |
| { | x + 3 > 0 | { | x > – 3 |
| y – 2 < 0 | y < 2 | ||
| x + 3 – y + 2 = 4 | y = x + 1 |
| { | x + 3 < 0 | { | x < – 3 |
| y + 2 > 0 | y > – 2 | ||
| – x – 3 – y – 2 = 4 | y = x + 9 |
| { | x + 3 < 0 | { | x < – 3 |
| y + 2 < 0 | y < – 2 | ||
| – x – 3 – y – 2 = 4 | y = – x – 9 |

As a result, we get a square whose center is (–3; 2), and the length of the diagonal is 8, and the diagonals are parallel to the coordinate axes.
From visual considerations we can conclude: that an equation of the form | X + a | + | at + b | = With; defines a square on the plane with center at point (– A; – b), diagonals parallel to the OX and OU axes, and the length of each diagonal is 2 With. Answer: (– 3; 2).
2. Solve the equation aх = 1
Answer: if a = 0, then there is no solution; If a= 0, then X = 1/ a
3. Solve the equation ( A 2 – 1) X = A + 1.
Solution.
It is not difficult to realize that when solving this equation it is enough to consider the following cases:
1) A= 1; then the equation takes the form OX = 2 and has no solution
2) A= – 1; we get OX = O, and obviously X– any.
1
3) if A = +
1, then X = –––
A
– 1
Answer:
If A= – 1, then X– any;
If A= 1, then there is no solution;
1
If A = +
1, then X = –––
A
– 1

3. Solutions to examples(from options C)
1. At what value of the parameter p does the equation | X 2 – 5X + 6 | + | X 2 – 5X + 4 | = r has four roots.
Consider the function y = | X 2 – 5X + 6 | + | X 2 – 5X + 4 |
Because X 2 – 5X + 6 = (X – 2)(X– 3) and X 2 – 5X + 4 = (X – 1)(X– 4), then y = | (X – 2)(X – 3) | + | (X – 1)(X– 4) |, we mark the roots of square trinomials on the number line
1 2 3 4 X
The number line is divided into 5 intervals
| { | x < 1 | { | x < 1 |
| y = x 2 – 5x + 6 + x 2 – 5x + 4 | y = 2x 2 – 10x + 10 |
| { | 1 < x < 2 | { | 1 < x < 2 |
| y = x 2 – 5x+ 6 – x 2 + 5x – 4 | y = 2 |
| { | 2 < x < 3 | { | 2 < x <3 |
| y = – 2x 2 + 10x – 10 | y = – x 2 + 5x – 6 – x 2 + 5x – 4 |
| { | 3 < x < 4 | { | 3 < x < 4 |
| y = 2 | y = x 2 – 5x + 6 – x 2 + 5x – 4 |
| { | x > 4 | { | x > 4 |
| y = 2x 2 – 10x + 10 | y= x 2 – 5x + 6 + x 2 –5x + 4 |
For case 3) X 0 = – b | 2a = 2, y 0 = 25: 2 + 25 – 10 = 2,5
So, (2.5; 2.5) are the coordinates of the vertex of the parabola y = – 2x 2 + 10x – 10.
Let's construct a graph of the function given by the equality

As can be seen from the figure, the original equation has four roots if 2 < A < 2,5
Answer: at 2 < A < 2,5
4. Independent work on levels
Level 1
1. Solve the equation X 2 – | x| = 6
2. For what integer values of a does the equation have a unique solution? Oh 2 – (A + 1) + A 2
+ A = 0?
Level 2
1. Solve the equation: | x – 5 | – | 2x + 3 | = 10
A –12) X 2 + 2 =
2(12 – A) has two different roots?
Level 3
1. Solve the equation | x – 5 | – | 2x + 3| = 10
2. Find all values of the parameter a for which the equation ( A – 12) X 2 + 2 = 2(12
– A) has two different roots?
5. Lesson summary
1. Definition of a module.
2. What does it mean to solve an equation with a parameter?
6. Homework assignment. C5 option No. 11 F.F. Lysenko. Mathematics, 2012
1. Systems of linear equations with a parameter
Systems of linear equations with a parameter are solved by the same basic methods as ordinary systems of equations: the substitution method, the method of adding equations, and the graphical method. Knowledge of the graphical interpretation of linear systems makes it easy to answer the question about the number of roots and their existence.
Example 1.
Find all values for parameter a for which the system of equations has no solutions.
(x + (a 2 – 3)y = a,
(x + y = 2.
Solution.
Let's look at several ways to solve this task.
1 way. We use the property: the system has no solutions if the ratio of the coefficients in front of x is equal to the ratio of the coefficients in front of y, but not equal to the ratio of the free terms (a/a 1 = b/b 1 ≠ c/c 1). Then we have:
1/1 = (a 2 – 3)/1 ≠ a/2 or system
(and 2 – 3 = 1,
(a ≠ 2.
From the first equation a 2 = 4, therefore, taking into account the condition that a ≠ 2, we get the answer.
Answer: a = -2.
Method 2. We solve by substitution method.
(2 – y + (a 2 – 3)y = a,
(x = 2 – y,
((a 2 – 3)y – y = a – 2,
(x = 2 – y.
After taking the common factor y out of brackets in the first equation, we get:
((a 2 – 4)y = a – 2,
(x = 2 – y.
The system has no solutions if the first equation has no solutions, that is
(and 2 – 4 = 0,
(a – 2 ≠ 0.
Obviously, a = ±2, but taking into account the second condition, the answer only comes with a minus answer.
Answer: a = -2.
Example 2.
Find all values for parameter a for which the system of equations has an infinite number of solutions.
(8x + ay = 2,
(ax + 2y = 1.
Solution.
According to the property, if the ratio of the coefficients of x and y is the same, and is equal to the ratio of the free members of the system, then it has an infinite number of solutions (i.e. a/a 1 = b/b 1 = c/c 1). Therefore 8/a = a/2 = 2/1. Solving each of the resulting equations, we find that a = 4 is the answer in this example.
Answer: a = 4.
2. Systems of rational equations with a parameter
Example 3.
(3|x| + y = 2,
(|x| + 2y = a.
Solution.
Let's multiply the first equation of the system by 2:
(6|x| + 2y = 4,
(|x| + 2y = a.
Subtracting the second equation from the first, we get 5|x| = 4 – a. This equation will have a unique solution for a = 4. In other cases, this equation will have two solutions (for a< 4) или ни одного (при а > 4).
Answer: a = 4.
Example 4.
Find all values of the parameter a for which the system of equations has a unique solution.
(x + y = a,
(y – x 2 = 1.
Solution.
We will solve this system using the graphical method. Thus, the graph of the second equation of the system is a parabola raised along the Oy axis upward by one unit segment. The first equation specifies the set of lines parallel to the line y = -x (Figure 1). It is clearly seen from the figure that the system has a solution if the straight line y = -x + a is tangent to the parabola at a point with coordinates (-0.5, 1.25). Substituting these coordinates into the straight line equation instead of x and y, we find the value of parameter a: 
1.25 = 0.5 + a;
Answer: a = 0.75.
Example 5.
Using the substitution method, find out at what value of the parameter a, the system has a unique solution.
(ax – y = a + 1,
(ax + (a + 2)y = 2.
Solution.
From the first equation we express y and substitute it into the second:
(y = ax – a – 1,
(ax + (a + 2)(ax – a – 1) = 2.
Let us reduce the second equation to the form kx = b, which will have a unique solution for k ≠ 0. We have:
ax + a 2 x – a 2 – a + 2ax – 2a – 2 = 2;
a 2 x + 3ax = 2 + a 2 + 3a + 2.
We represent the square trinomial a 2 + 3a + 2 as a product of brackets
(a + 2)(a + 1), and on the left we take x out of brackets:
(a 2 + 3a)x = 2 + (a + 2)(a + 1).
Obviously, a 2 + 3a should not be equal to zero, therefore,
a 2 + 3a ≠ 0, a(a + 3) ≠ 0, which means a ≠ 0 and ≠ -3.
Answer: a ≠ 0; ≠ -3.
Example 6.
Using the graphical solution method, determine at what value of parameter a the system has a unique solution.
(x 2 + y 2 = 9,
(y – |x| = a.
Solution.
Based on the condition, we construct a circle with a center at the origin and a radius of 3 unit segments, this is what is specified by the first equation of the system
x 2 + y 2 = 9. The second equation of the system (y = |x| + a) is a broken line. By using figure 2 We consider all possible cases of its location relative to the circle. It is easy to see that a = 3. 
Answer: a = 3.
Still have questions? Don't know how to solve systems of equations?
To get help from a tutor -.
The first lesson is free!
blog.site, when copying material in full or in part, a link to the original source is required.
“Linear Equation in Two Variables” - An equation containing two variables is called an equation in two variables. -What is an equation with two variables called? Give examples. -Which equation with two variables is called linear? Linear equation with two variables. Definition: An algorithm for proving that a given pair of numbers is a solution to the equation:
“Solving exponential equations” - Reducing to one base. Bracketing. T. Vieta. Graphic method. An exponential equation is an equation containing a variable with an exponent. Solving exponential equations. Oral work. ab+ac=a(b+c). Degrees. 2.Solve the equation: Property. Types and methods of solving exponential equations.
“Graphical method for solving equations” - Answer: one root, x = -1. Two roots. Solve graphically the equation (x+1)/(x-2)=2. Draw a graph of the function y=x?+6x+8. Workshop on solving equations graphically. Preparation for the test. Construct graphs of functions. Graph the function y=(x+1)/(x-2). 1. Move 8 to the right side of the equation. There are no roots.
“Solving entire equations” - “Equations in which there are roots, degrees, and an abyss of inequalities. Three great mathematicians. Good luck in further learning methods for solving equations. Axial symmetry is inherent in most species of plants and animals. Central. There are 2 types of symmetry in the animal world. Dictation. Axial. Identify methods for solving equations.
“Equations with logarithms” - Logarithmic equations. Solve equations orally. Formulas for converting logarithms. Equation. Definition. Logarithm tables. Definition of logarithm. Definition and properties of the logarithm. Slide rule. Function. Headphones or speakers. Scope of definition. Approaches to solution. Solve the equation. Gymnasium.
“Irrational equations” - For control purposes, the following were completed: No. 419 (c, d) Safiullina, No. 418 (c, d) Kulmukhametov, No. 420 (c, d) Shageev. Lesson 2 Solving systems of equations. Lesson 1 Topic: Solving irrational equations. 1.Which of the following equations are irrational: Objectives: To introduce students to solutions to some types of irrational equations.
There are 49 presentations in total
Maintaining your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please review our privacy practices and let us know if you have any questions.
Collection and use of personal information
Personal information refers to data that can be used to identify or contact a specific person.
You may be asked to provide your personal information at any time when you contact us.
Below are some examples of the types of personal information we may collect and how we may use such information.
What personal information do we collect:
- When you submit an application on the site, we may collect various information, including your name, phone number, email address, etc.
How we use your personal information:
- The personal information we collect allows us to contact you with unique offers, promotions and other events and upcoming events.
- From time to time, we may use your personal information to send important notices and communications.
- We may also use personal information for internal purposes, such as conducting audits, data analysis and various research in order to improve the services we provide and provide you with recommendations regarding our services.
- If you participate in a prize draw, contest or similar promotion, we may use the information you provide to administer such programs.
Disclosure of information to third parties
We do not disclose the information received from you to third parties.
Exceptions:
- If necessary - in accordance with the law, judicial procedure, in legal proceedings, and/or on the basis of public requests or requests from government authorities in the territory of the Russian Federation - to disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public importance purposes.
- In the event of a reorganization, merger, or sale, we may transfer the personal information we collect to the applicable successor third party.
Protection of personal information
We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as unauthorized access, disclosure, alteration and destruction.
Respecting your privacy at the company level
To ensure that your personal information is secure, we communicate privacy and security standards to our employees and strictly enforce privacy practices.