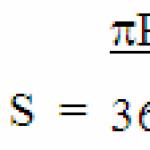Adjacent and vertical angles. Perpendicular lines. What are adjacent angles? Adjacent angles are always equal

1. Adjacent angles.

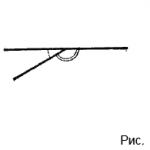
If we extend the side of any angle beyond its vertex, we get two angles (Fig. 72): ∠ABC and ∠CBD, in which one side BC is common, and the other two, AB and BD, form a straight line.

Two angles in which one side is common and the other two form a straight line are called adjacent angles.

Adjacent angles can also be obtained in this way: if we draw a ray from some point on a line (not lying on a given line), we will obtain adjacent angles.

For example, ∠ADF and ∠FDB are adjacent angles (Fig. 73).

Adjacent angles can have a wide variety of positions (Fig. 74).

Adjacent angles add up to a straight angle, so the sum of two adjacent angles is 180°

Hence, a right angle can be defined as an angle equal to its adjacent angle.

Knowing the size of one of the adjacent angles, we can find the size of the other angle adjacent to it.

For example, if one of the adjacent angles is 54°, then the second angle will be equal to:

180° - 54° = l26°.

2. Vertical angles.

If we extend the sides of the angle beyond its vertex, we get vertical angles. In Figure 75, the angles EOF and AOC are vertical; angles AOE and COF are also vertical.

Two angles are called vertical if the sides of one angle are continuations of the sides of the other angle.

Let ∠1 = \(\frac(7)(8)\) ⋅ 90°(Fig. 76). ∠2 adjacent to it will be equal to 180° - \(\frac(7)(8)\) ⋅ 90°, i.e. 1\(\frac(1)(8)\) ⋅ 90°.

In the same way, you can calculate what ∠3 and ∠4 are equal to.

∠3 = 180° - 1\(\frac(1)(8)\) ⋅ 90° = \(\frac(7)(8)\) ⋅ 90°;

∠4 = 180° - \(\frac(7)(8)\) ⋅ 90° = 1\(\frac(1)(8)\) ⋅ 90° (Fig. 77).

We see that ∠1 = ∠3 and ∠2 = ∠4.

You can solve several more of the same problems, and each time you will get the same result: the vertical angles are equal to each other.

However, to make sure that vertical angles are always equal to each other, it is not enough to consider individual numerical examples, since conclusions drawn from particular examples can sometimes be erroneous.

It is necessary to verify the validity of the properties of vertical angles by proof.

The proof can be carried out as follows (Fig. 78):

∠a+∠c= 180°;

∠b+∠c= 180°;

(since the sum of adjacent angles is 180°).

∠a+∠c = ∠b+∠c

(since the left side of this equality is equal to 180°, and its right side is also equal to 180°).

This equality includes the same angle With.

If we subtract equal amounts from equal quantities, then equal amounts will remain. The result will be: ∠a = ∠b, i.e. the vertical angles are equal to each other.

3. The sum of angles that have a common vertex.

In drawing 79, ∠1, ∠2, ∠3 and ∠4 are located on one side of a line and have a common vertex on this line. In sum, these angles make up a straight angle, i.e.

∠1 + ∠2 + ∠3 + ∠4 = 180°.

In Figure 80, ∠1, ∠2, ∠3, ∠4 and ∠5 have a common vertex. These angles add up to a full angle, i.e. ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 360°.

Other materials

Two angles placed on the same straight line and having the same vertex are called adjacent.

Otherwise, if the sum of two angles on one straight line is equal to 180 degrees and they have one side in common, then these are adjacent angles.

1 adjacent angle + 1 adjacent angle = 180 degrees.

Adjacent angles are two angles in which one side is common, and the other two sides generally form a straight line.

The sum of two adjacent angles is always 180 degrees. For example, if one angle is 60 degrees, then the second will necessarily be equal to 120 degrees (180-60).

Angles AOC and BOC are adjacent angles because all conditions for the characteristics of adjacent angles are met:

1.OS - common side of two corners

2.AO - side of the corner AOS, OB - side of the corner BOS. Together these sides form a straight line AOB.

3. There are two angles and their sum is 180 degrees.

Remembering the school geometry course, we can say the following about adjacent angles:

adjacent angles have one side in common, and the other two sides belong to the same straight line, that is, they are on the same straight line. If according to the figure, then the angles SOB and BOA are adjacent angles, the sum of which is always equal to 180, since they divide a straight angle, and a straight angle is always equal to 180.

Adjacent angles are an easy concept in geometry. Adjacent angles, an angle plus an angle, add up to 180 degrees.

Two adjacent angles will be one unfolded angle.

There are several more properties. With adjacent angles, problems are easy to solve and theorems to prove.

Adjacent angles are formed by drawing a ray from an arbitrary point on a straight line. Then this arbitrary point turns out to be the vertex of the angle, the ray turns out to be the common side of adjacent angles, and the straight line from which the ray is drawn turns out to be the two remaining sides of adjacent angles. Adjacent angles can be the same in the case of a perpendicular, or different in the case of an inclined beam. It is easy to understand that the sum of adjacent angles is equal to 180 degrees or simply a straight line. In another way, this angle can be explained by a simple example - you first walked in one direction in a straight line, then changed your mind, decided to go back and, turning 180 degrees, set off along the same straight line in the opposite direction.

So what is an adjacent angle? Definition:

Two angles with a common vertex and one common side are called adjacent, and the other two sides of these angles lie on the same straight line.

And a short video lesson that sensibly shows about adjacent angles, vertical angles, plus about perpendicular lines, which are a special case of adjacent and vertical angles

Adjacent angles are angles in which one side is common and the other is one line.

Adjacent angles are angles that depend on each other. That is, if the common side is slightly rotated, then one angle will decrease by several degrees and automatically the second angle will increase by the same number of degrees. This property of adjacent angles allows one to solve various problems in Geometry and carry out proofs of various theorems.

The total sum of adjacent angles is always 180 degrees.

From the geometry course, (as far as I remember in the 6th grade), two angles are called adjacent, in which one side is common, and the other sides are additional rays, the sum of adjacent angles is 180. Each of the two adjacent angles complements the other to an expanded angle. Example of adjacent angles:

Adjacent angles are two angles with a common vertex, one of whose sides is common, and the remaining sides lie on the same straight line (not coinciding). The sum of adjacent angles is one hundred and eighty degrees. In general, all this is very easy to find in Google or a geometry textbook.

Two angles are called adjacent if they have a common vertex and one side, and the other two sides form a straight line. The sum of adjacent angles is 180 degrees.

In the figure, angles AOB and BOC are adjacent.

Adjacent angles are those that have a common vertex, one common side, and the other sides are continuations of each other and form an extended angle. A remarkable property of adjacent angles is that the sum of these angles is always equal to 180 degrees.

Angles with a common vertex and one common side in geometry are called adjacent

The sum of adjacent angles is 180 degrees

It should be noted that adjacent angles have equal sines

To learn more about adjacent angles, read here

Each angle, depending on its size, has its own name:

Angle type	Size in degrees	Example
Spicy	Less than 90°
Straight	Equal to 90°. In a drawing, a right angle is usually denoted by a symbol drawn from one side of the angle to the other.
Blunt	More than 90° but less than 180°
Expanded	Equal to 180° A straight angle is equal to the sum of two right angles, and a right angle is half of a straight angle.
Convex	More than 180° but less than 360°
Full	Equal to 360°

The two angles are called adjacent, if they have one side in common, and the other two sides form a straight line:

Angles MOP And PON adjacent, since the beam OP- the common side, and the other two sides - OM And ON make up a straight line.

The common side of adjacent angles is called oblique to straight, on which the other two sides lie, only in the case when adjacent angles are not equal to each other. If adjacent angles are equal, then their common side will be perpendicular.

The sum of adjacent angles is 180°.

The two angles are called vertical, if the sides of one angle complement the sides of the other angle to straight lines:

Angles 1 and 3, as well as angles 2 and 4, are vertical.

Vertical angles are equal.

Let us prove that the vertical angles are equal:

The sum of ∠1 and ∠2 is a straight angle. And the sum of ∠3 and ∠2 is a straight angle. So these two amounts are equal:

∠1 + ∠2 = ∠3 + ∠2.

In this equality, there is an identical term on the left and right - ∠2. Equality will not be violated if this term on the left and right is omitted. Then we get it.

How to find an adjacent angle?

Mathematics is the oldest exact science, which is compulsorily studied in schools, colleges, institutes and universities. However, basic knowledge is always laid at school. Sometimes, the child is given quite complex tasks, but the parents are unable to help, because they simply forgot some things from mathematics. For example, how to find an adjacent angle based on the size of the main angle, etc. The problem is simple, but can cause difficulties in solving due to ignorance of which angles are called adjacent and how to find them.

Let's take a closer look at the definition and properties of adjacent angles, as well as how to calculate them from the data in the problem.

Definition and properties of adjacent angles

Two rays emanating from one point form a figure called a “plane angle”. In this case, this point is called the vertex of the angle, and the rays are its sides. If you continue one of the rays beyond the starting point in a straight line, then another angle is formed, which is called adjacent. Each angle in this case has two adjacent angles, since the sides of the angle are equivalent. That is, there is always an adjacent angle of 180 degrees.

The main properties of adjacent angles include

Adjacent angles have a common vertex and one side;
The sum of adjacent angles is always equal to 180 degrees or the number Pi if the calculation is carried out in radians;
The sines of adjacent angles are always equal;
The cosines and tangents of adjacent angles are equal but have opposite signs.

How to find adjacent angles

Usually three variations of problems are given to find the magnitude of adjacent angles

The value of the main angle is given;
The ratio of the main and adjacent angle is given;
The value of the vertical angle is given.

Each version of the problem has its own solution. Let's look at them.

The value of the main angle is given

If the problem specifies the value of the main angle, then finding the adjacent angle is very simple. To do this, just subtract the value of the main angle from 180 degrees, and you will get the value of the adjacent angle. This solution is based on the property of an adjacent angle - the sum of adjacent angles is always equal to 180 degrees.

If the value of the main angle is given in radians and the problem requires finding the adjacent angle in radians, then it is necessary to subtract the value of the main angle from the number Pi, since the value of the full unfolded angle of 180 degrees is equal to the number Pi.

The ratio of the main and adjacent angle is given

The problem may give the ratio of the main and adjacent angles instead of the degrees and radians of the main angle. In this case, the solution will look like a proportion equation:

We denote the proportion of the main angle as the variable “Y”.
The fraction related to the adjacent angle is denoted as the variable “X”.
The number of degrees that fall on each proportion will be denoted, for example, by “a”.
The general formula will look like this - a*X+a*Y=180 or a*(X+Y)=180.
We find the common factor of the equation “a” using the formula a=180/(X+Y).
Then we multiply the resulting value of the common factor “a” by the fraction of the angle that needs to be determined.

This way we can find the value of the adjacent angle in degrees. However, if you need to find a value in radians, then you simply need to convert the degrees to radians. To do this, multiply the angle in degrees by Pi and divide everything by 180 degrees. The resulting value will be in radians.

The value of the vertical angle is given

If the problem does not give the value of the main angle, but the value of the vertical angle is given, then the adjacent angle can be calculated using the same formula as in the first paragraph, where the value of the main angle is given.

A vertical angle is an angle that originates from the same point as the main one, but is directed in exactly the opposite direction. This results in a mirror image. This means that the vertical angle is equal in magnitude to the main one. In turn, the adjacent angle of the vertical angle is equal to the adjacent angle of the main angle. Thanks to this, the adjacent angle of the main angle can be calculated. To do this, simply subtract the vertical value from 180 degrees and get the value of the adjacent angle of the main angle in degrees.

If the value is given in radians, then it is necessary to subtract the value of the vertical angle from the number Pi, since the value of the full unfolded angle of 180 degrees is equal to the number Pi.

You can also read our useful articles and.

In the process of studying a geometry course, the concepts of “angle”, “vertical angles”, “adjacent angles” come up quite often. Understanding each of the terms will help you understand the problem and solve it correctly. What are adjacent angles and how to determine them?

Adjacent angles - definition of the concept

The term “adjacent angles” characterizes two angles formed by a common ray and two additional half-lines lying on the same straight line. All three rays come out from the same point. A common half-line is simultaneously a side of both one and the other angle.

Adjacent angles - basic properties

1. Based on the formulation of adjacent angles, it is easy to notice that the sum of such angles always forms a reverse angle, the degree measure of which is 180°:

If μ and η are adjacent angles, then μ + η = 180°.
Knowing the magnitude of one of the adjacent angles (for example, μ), you can easily calculate the degree measure of the second angle (η) using the expression η = 180° – μ.

2. This property of angles allows us to draw the following conclusion: an angle that is adjacent to a right angle will also be right.

3. Considering the trigonometric functions (sin, cos, tg, ctg), based on the reduction formulas for adjacent angles μ and η, the following is true:

sinη = sin(180° – μ) = sinμ,
cosη = cos(180° – μ) = -cosμ,
tgη = tg(180° – μ) = -tgμ,
ctgη = ctg(180° – μ) = -ctgμ.

Adjacent angles - examples

Example 1

Given a triangle with vertices M, P, Q – ΔMPQ. Find the angles adjacent to the angles ∠QMP, ∠MPQ, ∠PQM.

Let's extend each side of the triangle with a straight line.
Knowing that adjacent angles complement each other up to a reversed angle, we find out that:

adjacent to the angle ∠QMP is ∠LMP,

adjacent to the angle ∠MPQ is ∠SPQ,

adjacent to the angle ∠PQM is ∠HQP.

Example 2

The value of one adjacent angle is 35°. What is the degree measure of the second adjacent angle?

Two adjacent angles add up to 180°.
If ∠μ = 35°, then adjacent to it ∠η = 180° – 35° = 145°.

Example 3

Determine the values of adjacent angles if it is known that the degree measure of one of them is three times greater than the degree measure of the other angle.

Let us denote the magnitude of one (smaller) angle by – ∠μ = λ.
Then, according to the conditions of the problem, the value of the second angle will be equal to ∠η = 3λ.
Based on the basic property of adjacent angles, μ + η = 180° follows

λ + 3λ = μ + η = 180°,

λ = 180°/4 = 45°.

This means that the first angle is ∠μ = λ = 45°, and the second angle is ∠η = 3λ = 135°.