Important!
A function of the form “y = kx + b” is called a linear function.
The letter factors "k" and "b" are called numerical coefficients.
Instead of “k” and “b” there can be any numbers (positive, negative or fractions).
In other words, we can say that “y = kx + b” is a family of all possible functions, where instead of “k” and “b” there are numbers.
Examples of functions like “y = kx + b”.
- y = 5x + 3
- y = −x + 1
- y = x − 2
k = 2 3 b = −2 y = 0.5x k = 0.5 b = 0 Pay special attention to the "y = 0.5x" function in the table. They often make the mistake of looking for the numerical coefficient “b”.
When considering the function “y = 0.5x”, it is incorrect to say that there is no numerical coefficient “b” in the function.
The numerical coefficient "b" is always present in a function like "y = kx + b" always. In the function “y = 0.5x” the numerical coefficient “b” is zero.
How to graph a linear function
"y = kx + b"Remember!
The graph of the linear function “y = kx + b” is a straight line.
Since the graph of the function “y = kx + b” is a straight line, the function is called linear function.
From geometry, let us recall the axiom (a statement that does not require proof) that through any two points you can draw a straight line and, moreover, only one.
Based on the axiom above, it follows that in order to plot a function of the form
“y = kx + b” it will be enough for us to find only two points.For example let's build a graph of the function"y = −2x + 1".
Let's find the value of the function "y" for two arbitrary values "x". Let us substitute, for example, instead of “x” the numbers “0” and “1”.
Important!
When choosing arbitrary numeric values instead of “x”, it is better to take the numbers “0” and “1”. It's easy to do calculations with these numbers.
The resulting values “x” and “y” are the coordinates of the points on the function graph.
Let's write the obtained coordinates of the points “y = −2x + 1” into the table.
Let us mark the obtained points on the coordinate system.

Now let's draw a straight line through the marked points. This line will be the graph of the function “y = −2x + 1”.

How to solve problems on
linear function “y = kx + b”Let's consider the problem.
Graph the function “y = 2x + 3”. Find by graph:
- the value “y” corresponding to the value “x” equal to −1; 2; 3; 5 ;
- the value of "x" if the value of "y" is 1; 4; 0; −1.
First, let's plot the function “y = 2x + 3”.
We use the rules by which we are superior. To graph the function “y = 2x + 3” it is enough to find only two points.
Let's choose two arbitrary numeric values for “x”. For convenience of calculations, we will choose the numbers “0” and “1”.
Let's carry out the calculations and write their results in the table.
Let us mark the obtained points on the rectangular coordinate system.

Let's connect the resulting points with a straight line. The drawn straight line will be a graph of the function “y = 2x + 3”.

Now we work with the constructed graph of the function “y = 2x + 3”.
You need to find the value “y” corresponding to the value “x”,
which is equal to −1; 2; 3; 5 .- Ox" to zero (x = 0) ;
- substitute zero for “x” in the function formula and find the value “y”;
- Oy".
Instead of “x” in the formula of the function “y = −1.5x + 3”, let’s substitute the number zero.
Y(0) = −1.5 0 + 3 = 3
(0; 3) - coordinates of the point of intersection of the graph of the function “y = −1.5x + 3” with the axis “Oy”.Remember!
To find the coordinates of the intersection point of the graph of a function
with axis " Ox"(x axis) you need:- equate the coordinate of a point along the "" axis Oy" to zero (y = 0) ;
- substitute zero instead of “y” in the function formula and find the value of “x”;
- write down the obtained coordinates of the point of intersection with the axis " Oy".
Instead of “y” in the formula of the function “y = −1.5x + 3”, let’s substitute the number zero.
0 = −1.5x + 3
1.5x = 3 | :(1.5)
x = 3: 1.5
x = 2
(2; 0) - coordinates of the point of intersection of the graph of the function “y = −1.5x + 3” with the “Ox” axis.To make it easier to remember which coordinate of a point should be equated to zero, remember the “rule of opposites.”
Important!
If you need to find the coordinates of the point of intersection of the graph with the axis " Ox", then we equate “y” to zero.
And vice versa. If you need to find the coordinates of the point of intersection of the graph with the "" axis Oy", then we equate “x” to zero.
Schoolchildren are faced with the task of constructing a graph of a function at the very beginning of studying algebra and continue to build them year after year. Starting from the graph of a linear function, for which you need to know only two points, to a parabola, which already requires 6 points, a hyperbola and a sine wave. Every year the functions become more and more complex and it is no longer possible to construct their graphs using a template; it is necessary to carry out more complex studies using derivatives and limits.
Let's figure out how to find the graph of a function? To do this, let's start with the simplest functions, the graphs of which are plotted point by point, and then consider a plan for constructing more complex functions.
Graphing a Linear Function
To construct the simplest graphs, use a table of function values. The graph of a linear function is a straight line. Let's try to find the points on the graph of the function y=4x+5.
- To do this, let’s take two arbitrary values of the variable x, substitute them one by one into the function, find the value of the variable y and enter everything into the table.
- Take the value x=0 and substitute it into the function instead of x - 0. We get: y=4*0+5, that is, y=5, write this value in the table under 0. Similarly, take x=0, we get y=4*1+5 , y=9.
- Now, to build a graph of the function, you need to plot these points on the coordinate plane. Then you need to draw a straight line.
Graphing a Quadratic Function
A quadratic function is a function of the form y=ax 2 +bx +c, where x is a variable, a,b,c are numbers (a is not equal to 0). For example: y=x 2, y=x 2 +5, y=(x-3) 2, y=2x 2 +3x+5.
To construct the simplest quadratic function y=x 2, 5-7 points are usually taken. Let's take the values for the variable x: -2, -1, 0, 1, 2 and find the values of y in the same way as when constructing the first graph.
The graph of a quadratic function is called a parabola. After constructing graphs of functions, students have new tasks related to the graph.
Example 1: find the abscissa of the graph point of the function y=x 2 if the ordinate is 9. To solve the problem, you need to substitute its value 9 into the function instead of y. We get 9=x 2 and solve this equation. x=3 and x=-3. This can also be seen on the graph of the function.
Researching a function and plotting it
To plot graphs of more complex functions, you need to perform several steps aimed at studying it. To do this you need:
- Find the domain of definition of the function. The domain of definition is all the values that the variable x can take. Those points at which the denominator becomes 0 or the radical expression becomes negative should be excluded from the definition domain.
- Set whether the function is even or odd. Recall that an even function is one that meets the condition f(-x)=f(x). Its graph is symmetrical with respect to Oy. A function will be odd if it meets the condition f(-x)=-f(x). In this case, the graph is symmetrical about the origin.
- Find the points of intersection with the coordinate axes. In order to find the abscissa of the point of intersection with the Ox axis, it is necessary to solve the equation f(x) = 0 (the ordinate is equal to 0). To find the ordinate of the point of intersection with the Oy axis, it is necessary to substitute 0 in the function instead of the variable x (the abscissa is 0).
- Find the asymptotes of the function. An asyptote is a straight line that the graph approaches indefinitely, but never crosses. Let's figure out how to find the asymptotes of the graph of a function.
- Vertical asymptote of the straight line x=a
- Horizontal asymptote - straight line y=a
- Oblique asymptote - straight line of the form y=kx+b
- Find the extremum points of the function, the intervals of increase and decrease of the function. Let's find the extremum points of the function. To do this, you need to find the first derivative and equate it to 0. It is at these points that the function can change from increasing to decreasing. Let us determine the sign of the derivative on each interval. If the derivative is positive, then the graph of the function increases; if it is negative, it decreases.
- Find the inflection points of the function graph, the upward and downward convexity intervals.
Finding inflection points is now easier than ever. You just need to find the second derivative, then equate it to zero. Next we find the sign of the second derivative on each interval. If it is positive, then the graph of the function is convex downward, if it is negative, it is convex upward.
Function is one of the most important mathematical concepts. Function - variable dependency at from variable x, if each value X matches a single value at. Variable X called the independent variable or argument. Variable at called the dependent variable. All values of the independent variable (variable x) form the domain of definition of the function. All values that the dependent variable takes (variable y), form the range of values of the function.
Function graph call the set of all points of the coordinate plane, the abscissas of which are equal to the values of the argument, and the ordinates are equal to the corresponding values of the function, that is, the values of the variable are plotted along the abscissa axis x, and the values of the variable are plotted along the ordinate axis y. To do this, you need to know the properties of the function. The main properties of the function will be discussed below!
To plot a function graph, we recommend using our program -. If you have any questions while studying the material on this page, you can always ask them on ours. Also on the forum they will help you solve problems in mathematics, chemistry, and many other subjects!
Basic properties of functions.
1) Function domain and function range.
The domain of a function is the set of all valid valid argument values x(variable x), for which the function y = f(x) determined.
The range of a function is the set of all real values y, which the function accepts.
In elementary mathematics, functions are studied only on the set of real numbers.
2) Function zeros.
Function zero is the value of the argument at which the value of the function is equal to zero.
3) Intervals of constant sign of a function.
Intervals of constant sign of a function are sets of argument values on which the function values are only positive or only negative.
4) Monotonicity of the function.
An increasing function (in a certain interval) is a function in which a larger value of the argument from this interval corresponds to a larger value of the function.
A decreasing function (in a certain interval) is a function in which a larger value of the argument from this interval corresponds to a smaller value of the function.
5) Even (odd) function.
An even function is a function whose domain of definition is symmetrical with respect to the origin and for any X from the domain of definition the equality f(-x) = f(x). The graph of an even function is symmetrical about the ordinate.
An odd function is a function whose domain of definition is symmetrical with respect to the origin and for any X from the domain of definition the equality is true f(-x) = - f(x). The graph of an odd function is symmetrical about the origin.
6) Limited and unlimited functions.
A function is called bounded if there is a positive number M such that |f(x)| ≤ M for all values of x. If such a number does not exist, then the function is unlimited.
7) Periodicity of the function.
A function f(x) is periodic if there is a non-zero number T such that for any x from the domain of definition of the function the following holds: f(x+T) = f(x). This smallest number is called the period of the function. All trigonometric functions are periodic. (
The length of the segment on the coordinate axis is determined by the formula:
The length of a segment on the coordinate plane is found using the formula:
To find the length of a segment in a three-dimensional coordinate system, use the following formula:
The coordinates of the middle of the segment (for the coordinate axis only the first formula is used, for the coordinate plane - the first two formulas, for a three-dimensional coordinate system - all three formulas) are calculated using the formulas:
Function– this is a correspondence of the form y= f(x) between variable quantities, due to which each considered value of some variable quantity x(argument or independent variable) corresponds to a certain value of another variable, y(dependent variable, sometimes this value is simply called the value of the function). Note that the function assumes that one argument value X only one value of the dependent variable can correspond at. However, the same value at can be obtained with different X.
Function Domain– these are all the values of the independent variable (function argument, usually this X), for which the function is defined, i.e. its meaning exists. The area of definition is indicated D(y). By and large, you are already familiar with this concept. The domain of definition of a function is otherwise called the domain of permissible values, or VA, which you have long been able to find.
Function Range are all possible values of the dependent variable of a given function. Designated E(at).
Function increases on the interval in which a larger value of the argument corresponds to a larger value of the function. The function is decreasing on the interval in which a larger value of the argument corresponds to a smaller value of the function.
Intervals of constant sign of a function- these are the intervals of the independent variable over which the dependent variable retains its positive or negative sign.
Function zeros– these are the values of the argument at which the value of the function is equal to zero. At these points, the function graph intersects the abscissa axis (OX axis). Very often, the need to find the zeros of a function means the need to simply solve the equation. Also, often the need to find intervals of constancy of sign means the need to simply solve the inequality.
Function y = f(x) are called even X
![]()
This means that for any opposite values of the argument, the values of the even function are equal. The graph of an even function is always symmetrical with respect to the ordinate axis of the op-amp.
Function y = f(x) are called odd, if it is defined on a symmetric set and for any X from the domain of definition the equality holds:
![]()
This means that for any opposite values of the argument, the values of the odd function are also opposite. The graph of an odd function is always symmetrical about the origin.
The sum of the roots of even and odd functions (the points of intersection of the x-axis OX) is always equal to zero, because for every positive root X has a negative root - X.
It is important to note: some function does not have to be even or odd. There are many functions that are neither even nor odd. Such functions are called general functions, and for them none of the equalities or properties given above is satisfied.
Linear function is a function that can be given by the formula:
The graph of a linear function is a straight line and in the general case looks like this (an example is given for the case when k> 0, in this case the function is increasing; for the occasion k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону - слева направо):

Graph of a quadratic function (Parabola)
The graph of a parabola is given by a quadratic function:
A quadratic function, like any other function, intersects the OX axis at the points that are its roots: ( x 1 ; 0) and ( x 2 ; 0). If there are no roots, then the quadratic function does not intersect the OX axis; if there is only one root, then at this point ( x 0 ; 0) the quadratic function only touches the OX axis, but does not intersect it. The quadratic function always intersects the OY axis at the point with coordinates: (0; c). The graph of a quadratic function (parabola) may look like this (the figure shows examples that do not exhaust all possible types of parabolas):

Wherein:
- if the coefficient a> 0, in function y = ax 2 + bx + c, then the branches of the parabola are directed upward;
- if a < 0, то ветви параболы направлены вниз.
The coordinates of the vertex of a parabola can be calculated using the following formulas. X tops (p- in the pictures above) parabolas (or the point at which the quadratic trinomial reaches its largest or smallest value):
Igrek tops (q- in the figures above) parabolas or the maximum if the branches of the parabola are directed downwards ( a < 0), либо минимальное, если ветви параболы направлены вверх (a> 0), the value of the quadratic trinomial:
Graphs of other functions
Power function
Here are some examples of graphs of power functions:

Inversely proportional is a function given by the formula:
Depending on the sign of the number k An inversely proportional dependence graph can have two fundamental options:

Asymptote is a line that the graph of a function approaches infinitely close to but does not intersect. The asymptotes for the inverse proportionality graphs shown in the figure above are the coordinate axes to which the graph of the function approaches infinitely close, but does not intersect them.
Exponential function with base A is a function given by the formula:
a The graph of an exponential function can have two fundamental options (we also give examples, see below):

Logarithmic function is a function given by the formula:
Depending on whether the number is greater or less than one a The graph of a logarithmic function can have two fundamental options:

Graph of a function y = |x| as follows:

Graphs of periodic (trigonometric) functions
Function at = f(x) is called periodic, if there is such a non-zero number T, What f(x + T) = f(x), for anyone X from the domain of the function f(x). If the function f(x) is periodic with period T, then the function:
Where: A, k, b are constant numbers, and k not equal to zero, also periodic with period T 1, which is determined by the formula:
Most examples of periodic functions are trigonometric functions. We present graphs of the main trigonometric functions. The following figure shows part of the graph of the function y= sin x(the entire graph continues indefinitely left and right), graph of the function y= sin x called sinusoid:

Graph of a function y=cos x called cosine. This graph is shown in the following figure. Since the sine graph continues indefinitely along the OX axis to the left and right:

Graph of a function y= tg x called tangentoid. This graph is shown in the following figure. Like the graphs of other periodic functions, this graph repeats indefinitely along the OX axis to the left and right.

And finally, the graph of the function y=ctg x called cotangentoid. This graph is shown in the following figure. Like the graphs of other periodic and trigonometric functions, this graph repeats indefinitely along the OX axis to the left and right.

Successful, diligent and responsible implementation of these three points will allow you to show an excellent result at the CT, the maximum of what you are capable of.
Found a mistake?
If you think you have found an error in the training materials, please write about it by email. You can also report an error on the social network (). In the letter, indicate the subject (physics or mathematics), the name or number of the topic or test, the number of the problem, or the place in the text (page) where, in your opinion, there is an error. Also describe what the suspected error is. Your letter will not go unnoticed, the error will either be corrected, or you will be explained why it is not an error.
What do the words mean? "set a function"? They mean: explain to everyone who wants to know what specific function we are talking. Moreover, explain clearly and unambiguously!
How can I do that? How set a function?
You can write a formula. You can draw a graph. You can make a table. Any way is some rule by which we can find out the value of the i for the x value we have chosen. Those. "set function", this means to show the law, the rule by which an x turns into a y.
Usually, in a variety of tasks there are already ready functions. They give us have already been set. Decide for yourself, yes, decide.) But... Most often, schoolchildren (and even students) work with formulas. They get used to it, you know... They get so used to it that any elementary question related to a different way of specifying a function immediately upsets the person...)
To avoid such cases, it makes sense to understand different ways of specifying functions. And, of course, apply this knowledge to “tricky” questions. It's quite simple. If you know what a function is...)
Go?)
Analytical method of specifying a function.
The most universal and powerful way. A function defined analytically this is the function that is given formulas. Actually, this is the whole explanation.) Functions that are familiar to everyone (I want to believe!), for example: y = 2x, or y = x 2 etc. and so on. are specified analytically.
By the way, not every formula can define a function. Not every formula meets the strict condition from the definition of a function. Namely - for every X there can only be one igrek. For example, in the formula y = ±x, For one values x=2, it turns out two y values: +2 and -2. This formula cannot define a unique function. As a rule, they don’t work with multi-valued functions in this branch of mathematics, in calculus.
What is good about the analytical way of specifying a function? Because if you have a formula, you know about the function All! You can make a sign. Build a graph. Explore this feature in full. Predict exactly where and how this function will behave. All mathematical analysis is based on this method of specifying functions. Let's say, taking a derivative of a table is extremely difficult...)
The analytical method is quite familiar and does not create problems. Perhaps there are some variations of this method that students encounter. I'm talking about parametric and implicit functions.) But such functions are in a special lesson.
Let's move on to less familiar ways of specifying a function.
Tabular method of specifying a function.
As the name suggests, this method is a simple sign. In this table, each x corresponds to ( is put in accordance) some meaning of the game. The first line contains the values of the argument. The second line contains the corresponding function values, for example:
Table 1.
| x | - 3 | - 1 | 0 | 2 | 3 | 4 |
| y | 5 | 2 | - 4 | - 1 | 6 | 5 |
Please pay attention! In this example, the game depends on X anyhow. I came up with this on purpose.) There is no pattern. It's okay, it happens. Means, exactly I have specified this specific function. Exactly I established a rule according to which an X turns into a Y.
You can make up another a plate containing a pattern. This sign will indicate other function, for example:
Table 2.
| x | - 3 | - 1 | 0 | 2 | 3 | 4 |
| y | - 6 | - 2 | 0 | 4 | 6 | 8 |
Did you catch the pattern? Here all the values of the game are obtained by multiplying x by two. Here is the first “tricky” question: can a function defined using Table 2 be considered a function y = 2x? Think for now, the answer will be below, in a graphical way. It's all very clear there.)
What's good tabular method of specifying a function? Yes, because you don’t need to count anything. Everything has already been calculated and written in the table.) But there is nothing more good. We don't know the value of the function for X's, which are not in the table. In this method, such x values are simply does not exist. By the way, this is a hint to a tricky question.) We cannot find out how the function behaves outside the table. We can't do anything. And the clarity of this method leaves much to be desired... The graphical method is good for clarity.
Graphical way to specify a function.
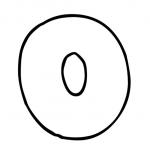
In this method, the function is represented by a graph. The argument (x) is plotted along the abscissa axis, and the function value (y) is plotted along the ordinate axis. According to the schedule, you can also choose any X and find the corresponding value at. The graph can be any, but... not just any one.) We work only with unambiguous functions. The definition of such a function clearly states: each X is put in accordance the only one at. One one game, not two, or three... For example, let's look at the circle graph:
A circle is like a circle... Why shouldn't it be the graph of a function? Let's find which game will correspond to the value of X, for example, 6? We move the cursor over the graph (or touch the drawing on the tablet), and... we see that this x corresponds two game meanings: y=2 and y=6.
Two and six! Therefore, such a graph will not be a graphical assignment of the function. On one x accounts for two game. This graph does not correspond to the definition of a function.
But if the unambiguity condition is met, the graph can be absolutely anything. For example:
This same crookedness is the law by which an X can be converted into a Y. Unambiguous. We wanted to know the meaning of the function for x = 4, For example. We need to find the four on the x-axis and see which game corresponds to this x. We move the mouse over the figure and see that the function value at For x=4 equals five. We don’t know what formula determines this transformation of an X into a Y. And it is not necessary. Everything is set by the schedule.
Now we can return to the “tricky” question about y=2x. Let's plot this function. Here he is:
Of course, when drawing this graph we did not take an infinite number of values X. We took several values and calculated y, made a sign - and everything is ready! The most literate people took only two values of X! And rightly so. For a straight line you don’t need more. Why the extra work?
But we knew for sure what x could be anyone. Integer, fractional, negative... Any. This is according to the formula y=2x it is seen. Therefore, we boldly connected the points on the graph with a solid line.
If the function is given to us by Table 2, then we will have to take the values of x only from the table. Because other X's (and Y's) are not given to us, and there is nowhere to get them. These values are not present in this function. The schedule will work out from points. We move the mouse over the figure and see the graph of the function specified in Table 2. I didn’t write the x-y values on the axes, you’ll figure it out, cell by cell?)
Here is the answer to the “tricky” question. Function specified by Table 2 and function y=2x - different.
The graphical method is good for its clarity. You can immediately see how the function behaves, where it increases. where it decreases. From the graph you can immediately find out some important characteristics of the function. And in the topic with derivatives, tasks with graphs are all over the place!
In general, analytical and graphical methods of defining a function go hand in hand. Working with the formula helps to build a graph. And the graph often suggests solutions that you wouldn’t even notice in the formula... We will be friends with graphs.)
Almost any student knows the three ways to define a function that we just looked at. But to the question: “And the fourth!?” - freezes thoroughly.)
There is such a way.
Verbal description of the function.
Yes Yes! The function can be quite unambiguously specified in words. The great and mighty Russian language is capable of a lot!) Let's say the function y=2x can be specified with the following verbal description: Each real value of the argument x is associated with its double value. Like this! The rule is established, the function is specified.
Moreover, you can verbally specify a function that is extremely difficult, if not impossible, to define using a formula. For example: Each value of the natural argument x is associated with the sum of the digits that make up the value of x. For example, if x=3, That y=3. If x=257, That y=2+5+7=14. And so on. It is problematic to write this down in a formula. But the sign is easy to make. And build a schedule. By the way, the graph looks funny...) Try it.
The method of verbal description is quite exotic. But sometimes it does. I brought it here to give you confidence in unexpected and unusual situations. You just need to understand the meaning of the words "function specified..." Here it is, this meaning:
If there is a law of one-to-one correspondence between X And at- that means there is a function. What law, in what form it is expressed - a formula, a tablet, a graph, words, songs, dances - does not change the essence of the matter. This law allows you to determine the corresponding value of the Y from the value of X. All.
Now we will apply this deep knowledge to some non-standard tasks.) As promised at the beginning of the lesson.
Exercise 1:
The function y = f(x) is given by Table 1:
Table 1.
Find the value of the function p(4), if p(x)= f(x) - g(x)
If you can’t understand what’s what at all, read the previous lesson “What is a function?” It is written very clearly about such letters and brackets.) And if only the tabular form confuses you, then we’ll sort it out here.
From the previous lesson it is clear that if, p(x) = f(x) - g(x), That p(4) = f(4) - g(4). Letters f And g means the rules according to which each X is assigned its own game. For each letter ( f And g) - yours rule. Which is given by the corresponding table.
Function value f(4) determined from Table 1. This will be 5. Function value g(4) determined according to Table 2. This will be 8. The most difficult thing remains.)
p(4) = 5 - 8 = -3
This is the correct answer.
Solve the inequality f(x) > 2
That's it! It is necessary to solve the inequality, which (in the usual form) is brilliantly absent! All that remains is to either give up the task or turn on your head. We choose the second and discuss.)
What does it mean to solve inequality? This means finding all the values of x at which the condition given to us is satisfied f(x) > 2. Those. all function values ( at) must be greater than two. And on our chart we have every game... And there are more twos, and less... And let’s, for clarity, draw a border along this two! We move the cursor over the drawing and see this border.
Strictly speaking, this boundary is the graph of the function y=2, but that's not the point. The important thing is that now the graph shows very clearly where, at what X's, function values, i.e. y, more than two. They are more X > 3. At X > 3 our whole function passes higher borders y=2. That's the solution. But it’s too early to turn off your head!) I still need to write down the answer...
The graph shows that our function does not extend left and right to infinity. The points at the ends of the graph indicate this. The function ends there. Therefore, in our inequality, all the X’s that go beyond the limits of the function have no meaning. For the function of these X's does not exist. And we, in fact, solve the inequality for the function...
The correct answer will be:
3 < X ≤ 6
Or, in another form:
X ∈ (3; 6]
Now everything is as it should be. Three is not included in the answer, because the original inequality is strict. And the six turns on, because and the function at six exists, and the inequality condition is satisfied. We have successfully solved an inequality that (in the usual form) does not exist...
This is how some knowledge and elementary logic saves you in non-standard cases.)