projeksioni vektori në një bosht quhet vektor, i cili fitohet duke shumëzuar projeksionin skalar të një vektori në këtë bosht dhe vektorin njësi të këtij boshti. Për shembull, nëse një x është projeksion skalar vektoriale a në boshtin x, pastaj një x i- projeksioni i tij vektorial në këtë bosht.
Shënoni projeksion vektorial ashtu si vetë vektori, por me indeksin e boshtit mbi të cilin projektohet vektori. Pra, projeksioni vektorial i vektorit a në boshtin x shënojmë a x ( me vaj një shkronjë që tregon një vektor dhe një nënshkrim të emrit të boshtit) ose (një shkronjë jo e trashë që tregon një vektor, por me një shigjetë në krye (!) dhe një nënshkrim të emrit të boshtit).
Projeksion skalar vektor për bosht quhet numri, vlera absolute e së cilës është e barabartë me gjatësinë e segmentit të boshtit (në shkallën e zgjedhur) të mbyllur midis projeksioneve të pikës fillestare dhe pikës fundore të vektorit. Zakonisht në vend të shprehjes projeksion skalar thjesht thuaj - projeksioni. Projeksioni shënohet me të njëjtën shkronjë si vektori i projektuar (në shkrimin normal, jo të trashë), me një nënshkrim (zakonisht) të emrit të boshtit në të cilin projektohet ky vektor. Për shembull, nëse një vektor projektohet në boshtin x a, atëherë projeksioni i tij shënohet x. Kur projektoni të njëjtin vektor në një bosht tjetër, nëse boshti është Y, projeksioni i tij do të shënohet si y.
Për të llogaritur projeksionin vektoriale në një bosht (për shembull, boshti X) është e nevojshme të zbritet koordinata e pikës së fillimit nga koordinata e pikës fundore të saj, d.m.th.
dhe x \u003d x k - x n.
Projeksioni i një vektori në një bosht është një numër. Për më tepër, projeksioni mund të jetë pozitiv nëse vlera e x k është më e madhe se vlera e x n,
negative nëse vlera e x k është më e vogël se vlera e x n
dhe e barabartë me zero nëse x k është e barabartë me x n.
Projeksioni i një vektori mbi një bosht mund të gjendet gjithashtu duke ditur modulin e vektorit dhe këndin që ai bën me atë bosht.
Nga figura mund të shihet se a x = a Cos α
domethënë, projeksioni i vektorit në bosht është i barabartë me produktin e modulit të vektorit dhe kosinusit të këndit ndërmjet drejtimit të boshtit dhe drejtimi i vektorit. Nëse këndi është akut, atëherë
Cos α > 0 dhe a x > 0, dhe nëse është i mpirë, atëherë kosinusi i një këndi të mpirë është negativ, dhe projeksioni i vektorit në bosht do të jetë gjithashtu negativ.
Këndet e numëruara nga boshti në drejtim të kundërt të akrepave të orës konsiderohen pozitive, dhe në drejtim - negative. Sidoqoftë, meqenëse kosinusi është një funksion çift, domethënë Cos α = Cos (− α), kur llogariten projeksionet, këndet mund të numërohen si në drejtim të akrepave të orës ashtu edhe në të kundërt.
Për të gjetur projeksionin e një vektori në një bosht, moduli i këtij vektori duhet të shumëzohet me kosinusin e këndit midis drejtimit të boshtit dhe drejtimit të vektorit.
Koordinatat vektoriale janë koeficientët e kombinimit të vetëm linear të mundshëm të vektorëve bazë në sistemin e zgjedhur koordinativ të barabartë me vektorin e dhënë.
ku janë koordinatat e vektorit.
Prodhimi me pika i vektorëve
PRODUKTI I SHKOLLIT TË VEKTORËVE[- në dimensione të fundme hapësirë vektoriale përkufizohet si shuma e produkteve të përbërësve të njëjtë të shumëzuarit vektorët.
Për shembull, S. p. a = (a 1 , ..., a n) dhe b = (b 1 , ..., b n):
(a , b ) = a 1 b 1 + a 2 b 2 + ... + a n b n
Boshti është drejtimi. Prandaj, projeksioni në një bosht ose në një vijë të drejtuar konsiderohet i njëjtë. Projeksioni mund të jetë algjebrik ose gjeometrik. Në terma gjeometrikë, projeksioni i një vektori në një bosht kuptohet si një vektor, dhe në terma algjebrikë, është një numër. Kjo do të thotë, përdoren konceptet e projeksionit të një vektori në një bosht dhe projeksioni numerik i një vektori në një bosht.
Nëse kemi një bosht L dhe një vektor jozero A B → , atëherë mund të ndërtojmë një vektor A 1 B 1 ⇀ , duke treguar projeksionet e pikave të tij A 1 dhe B 1 .
A 1 B → 1 do të jetë projeksioni i vektorit A B → në L .
Përkufizimi 1
Projeksioni i vektorit në bosht quhet një vektor, fillimi dhe fundi i të cilit janë projeksionet e fillimit dhe të fundit të vektorit të dhënë. n p L A B → → është zakon të shënohet projeksioni i A B → në L . Për të ndërtuar një projeksion në L, hidhni pingulet në L.
Shembulli 1
Një shembull i projeksionit të një vektori në një bosht.
Në planin koordinativ O x y, specifikohet një pikë M 1 (x 1, y 1). Është e nevojshme të ndërtohen projeksione në O x dhe O y për imazhin e vektorit të rrezes së pikës M 1 . Le të marrim koordinatat e vektorëve (x 1 , 0) dhe (0 , y 1) .

Nëse bëhet fjalë për projeksionin e a → mbi një b jozero → ose për projeksionin e a → në drejtimin b → , atëherë nënkuptojmë projeksionin e a → në boshtin me të cilin drejtimi b → përkon. Projeksioni a → në vijën e përcaktuar me b → shënohet n p b → a → → . Dihet se kur këndi është ndërmjet a → dhe b → , mund të konsiderojmë n p b → a → → dhe b → bashkëdrejtues. Në rastin kur këndi është i mpirë, n p b → a → → dhe b → kanë drejtim të kundërt. Në situatën e pingulitetit a → dhe b → , dhe a → është zero, projeksioni i a → përgjatë drejtimit b → është një vektor zero.
Karakteristika numerike e projeksionit të një vektori në një bosht është projeksioni numerik i një vektori në një bosht të caktuar.
Përkufizimi 2
Projeksioni numerik i vektorit mbi bosht thirrni një numër që është i barabartë me prodhimin e gjatësisë së një vektori të caktuar dhe kosinusit të këndit ndërmjet vektorit të dhënë dhe vektorit që përcakton drejtimin e boshtit.
Projeksioni numerik i A B → në L shënohet n p L A B → , dhe a → në b → - n p b → a → .
Bazuar në formulën, marrim n p b → a → = a → · cos a → , b → ^ , nga ku a → është gjatësia e vektorit a → , a ⇀ , b → ^ është këndi ndërmjet vektorëve a → dhe b → .
Marrim formulën për llogaritjen e projeksionit numerik: n p b → a → = a → · cos a → , b → ^ . Është i zbatueshëm për gjatësitë e njohura a → dhe b → dhe këndin ndërmjet tyre. Formula është e zbatueshme për koordinatat e njohura a → dhe b → , por ekziston një version i thjeshtuar i saj.
Shembulli 2
Gjeni projeksionin numerik a → në një vijë të drejtë në drejtimin b → me gjatësi a → të barabartë me 8 dhe këndi ndërmjet tyre është 60 gradë. Me kusht kemi një ⇀ = 8 , a ⇀ , b → ^ = 60 ° . Pra, ne i zëvendësojmë vlerat numerike në formulën n p b ⇀ a → = a → · cos a → , b → ^ = 8 · cos 60 ° = 8 · 1 2 = 4.
Përgjigje: 4.
Me cos të njohur (a → , b → ^) = a ⇀ , b → a → · b → , kemi a → , b → si prodhim skalar të a → dhe b → . Duke ndjekur formulën n p b → a → = a → · cos a ⇀ , b → ^ , mund të gjejmë projeksionin numerik a → të drejtuar përgjatë vektorit b → dhe të marrim n p b → a → = a → , b → b → . Formula është ekuivalente me përkufizimin e dhënë në fillim të klauzolës.
Përkufizimi 3
Projeksioni numerik i vektorit a → në boshtin që përkon në drejtim me b → është raporti i prodhimit skalar të vektorëve a → dhe b → me gjatësinë b → . Formula n p b → a → = a → , b → b → është e zbatueshme për gjetjen e projeksionit numerik të a → në një vijë të drejtë që përkon në drejtim me b → , me koordinata të njohura a → dhe b →.
Shembulli 3
Jepet b → = (- 3 , 4) . Gjeni projeksionin numerik a → = (1 , 7) në L .
Zgjidhje
Në planin koordinativ n p b → a → = a → , b → b → ka formën n p b → a → = a → , b → b → = a x b x + a y b y b x 2 + b y 2 , me a → = (a x , a y ) dhe b → = b x, b y. Për të gjetur projeksionin numerik të vektorit a → në boshtin L, ju nevojiten: n p L a → = n p b → a → = a → , b → b → = a x b x + a y b y b x 2 + b y 2 = 1 (- 3) + 7 4 (- 3) 2 + 4 2 = 5 .
Përgjigje: 5.
Shembulli 4
Gjeni projeksionin a → në L , që përkon me drejtimin b → , ku janë a → = - 2 , 3 , 1 dhe b → = (3 , - 2 , 6) . Jepet një hapësirë tredimensionale.
Zgjidhje
Jepet a → = a x , a y , a z dhe b → = b x , b y , b z njehso produktin skalar: a ⇀ , b → = a x b x + a y b y + a z b z . Ne gjejmë gjatësinë b → me formulën b → = b x 2 + b y 2 + b z 2. Nga kjo rrjedh se formula për përcaktimin e projeksionit numerik a → do të jetë: n p b → a ⇀ = a → , b → b → = a x b x + a y b y + a z b z b x 2 + b y 2 + b z 2 .
Zëvendësojmë vlerat numerike: n p L a → = n p b → a → = (- 2) 3 + 3 (- 2) + 1 6 3 2 + (- 2) 2 + 6 2 = - 6 49 = - 6 7 .
Përgjigje: - 6 7 .
Le të shohim lidhjen midis a → në L dhe gjatësisë së projeksionit të a → në L . Vizatoni një bosht L duke shtuar a → dhe b → nga një pikë në L , pas së cilës vizatojmë një vijë pingule nga fundi i a → në L dhe projektojmë në L . Ekzistojnë 5 variacione të imazhit:

E para rasti kur a → = n p b → a → → do të thotë a → = n p b → a → → , pra n p b → a → = a → cos (a , → b → ^) = a → cos 0 ° = a → = n p b → a → → .
Së dyti rasti nënkupton përdorimin e n p b → a → ⇀ = a → cos a → , b → , pra n p b → a → = a → cos (a → , b →) ^ = n p b → a → → .
Së treti rasti shpjegon se kur n p b → a → → = 0 → marrim n p b ⇀ a → = a → cos (a → , b → ^) = a → cos 90 ° = 0, atëherë n p b → a → → = 0 dhe n p b → a → = 0 = n p b → a → → .
Së katërti rasti tregon n p b → a → → = a → cos (180 ° - a → , b → ^) = - a → cos (a → , b → ^) , vijon n p b → a → = a → cos (a → , b → ^) = - n p b → a → → .
E pesta rasti tregon a → = n p b → a → → , që do të thotë a → = n p b → a → → , pra kemi n p b → a → = a → cos a → , b → ^ = a → cos 180 ° = - a → = - n p b → a → .
Përkufizimi 4
Projeksioni numerik i vektorit a → në boshtin L , i cili drejtohet si b → , ka kuptimin:
- gjatësia e projeksionit të vektorit a → në L me kusht që këndi ndërmjet a → dhe b → të jetë më i vogël se 90 gradë ose i barabartë me 0: n p b → a → = n p b → a → → me kushtin 0 ≤ (a → , b →) ^< 90 ° ;
- zero nën kushtin e pingulitetit a → dhe b → : n p b → a → = 0 kur (a → , b → ^) = 90 ° ;
- gjatësia e projeksionit a → në L, herë -1 kur ka një kënd të mpirë ose të rrafshuar të vektorëve a → dhe b → : n p b → a → = - n p b → a → → me kushtin 90°< a → , b → ^ ≤ 180 ° .
Shembulli 5
Jepet gjatësia e projeksionit a → mbi L , e barabartë me 2 . Gjeni projeksionin numerik a → duke pasur parasysh se këndi është 5 π 6 radian.
Zgjidhje
Mund të shihet nga kushti që ky kënd të jetë i mpirë: π 2< 5 π 6 < π . Тогда можем найти числовую проекцию a → на L: n p L a → = - n p L a → → = - 2 .
Përgjigje: - 2.
Shembulli 6
Jepet një rrafsh O x y z me gjatësi të vektorit a → i barabartë me 6 3 , b → (- 2 , 1 , 2) me kënd 30 gradë. Gjeni koordinatat e projeksionit a → në boshtin L.
Zgjidhje
Së pari, ne llogarisim projeksionin numerik të vektorit a → : n p L a → = n p b → a → = a → cos (a → , b →) ^ = 6 3 cos 30 ° = 6 3 3 2 = 9 .
Sipas kushtit, këndi është i mprehtë, atëherë projeksioni numerik a → = është gjatësia e projeksionit të vektorit a → : n p L a → = n p L a → → = 9 . Ky rast tregon se vektorët n p L a → → dhe b → janë të bashkëdrejtuar, që do të thotë se ekziston një numër t për të cilin barazia është e vërtetë: n p L a → → = t · b → . Nga këtu shohim se n p L a → → = t b → , kështu që mund të gjejmë vlerën e parametrit t: t = n p L a → → b → = 9 (- 2) 2 + 1 2 + 2 2 = 9 9 = 3.
Atëherë n p L a → → = 3 b → me koordinatat e projeksionit të vektorit a → në boshtin L janë b → = (- 2, 1, 2), ku është e nevojshme të shumëzohen vlerat me 3 Kemi n p L a → → = (- 6 , 3 , 6). Përgjigje: (- 6 , 3 , 6) .
Është e nevojshme të përsëriten informacionet e studiuara më parë në lidhje me gjendjen e kolinearitetit të vektorit.
Nëse vëreni një gabim në tekst, ju lutemi theksoni atë dhe shtypni Ctrl+Enter
Zgjidhja e problemeve mbi ekuilibrin e forcave konvergjente duke ndërtuar poligone me forcë të mbyllur shoqërohet me ndërtime të rënda. Një metodë universale për zgjidhjen e problemeve të tilla është kalimi në përcaktimin e projeksioneve të forcave të dhëna në akset koordinative dhe funksionimin me këto projeksione. Boshti quhet një vijë e drejtë, së cilës i caktohet një drejtim i caktuar.
Projeksioni i një vektori mbi një bosht është një vlerë skalare, e cila përcaktohet nga segmenti i boshtit të prerë nga pingulët e rënë mbi të nga fillimi dhe fundi i vektorit.
Projeksioni i një vektori konsiderohet pozitiv nëse drejtimi nga fillimi i projeksionit deri në fund të tij përkon me drejtimin pozitiv të boshtit. Projeksioni i një vektori konsiderohet negativ nëse drejtimi nga fillimi i projeksionit deri në fund të tij është i kundërt me drejtimin pozitiv të boshtit.
Kështu, projeksioni i forcës në boshtin koordinativ është i barabartë me produktin e modulit të forcës dhe kosinusit të këndit midis vektorit të forcës dhe drejtimit pozitiv të boshtit.
Konsideroni një numër rastesh të projektimit të forcave në një bosht:
Vektori i forcës F(Fig. 15) bën një kënd akut me drejtimin pozitiv të boshtit x.

Për të gjetur projeksionin, nga fillimi dhe fundi i vektorit të forcës i ulim pingulet në bosht. oh; marrim
1. Fx = F cosα
Projeksioni i vektorit në këtë rast është pozitiv
Forcë F(Fig. 16) është me drejtim pozitiv të boshtit X këndi i mpirë α.

Pastaj F x= F cos α, por meqenëse α = 180 0 - φ,
F x= F cosα = F cos180 0 - φ =- F cos phi.
Projeksioni i forcës F për bosht oh në këtë rast është negative.
Forcë F(Fig. 17) pingul me boshtin oh.

Projeksioni i forcës F në bosht X zero
F x= F cos 90° = 0.
Forca e vendosur në një aeroplan si(Fig. 18), mund të projektohet në dy akse koordinative oh dhe OU.

Forcë F mund të ndahet në komponentë: F x dhe F y . Moduli vektorial F x është e barabartë me projeksionin vektorial F për bosht kau, dhe moduli i vektorit F y është i barabartë me projeksionin e vektorit F për bosht o.
Nga Δ OAB: F x= F cosα, F x= F siνα.
Nga Δ SLA: F x= F cos phi, F x= F sin phi.
Moduli i forcës mund të gjendet duke përdorur teoremën e Pitagorës:
![]()
Projeksioni i shumës vektoriale ose rezultantes në çdo bosht është i barabartë me shumën algjebrike të projeksioneve të termave të vektorëve në të njëjtin bosht.
Merrni parasysh forcat konverguese F 1 , F 2 , F 3, dhe F 4, (Fig. 19, a). Shuma gjeometrike, ose rezultante, e këtyre forcave F përcaktohet nga ana mbyllëse e poligonit të forcës


Bie nga kulmet e poligonit të forcës në bosht x pingulet.
Duke marrë parasysh projeksionet e marra të forcave direkt nga ndërtimi i përfunduar, kemi
F= F 1x+ F 2x+ F 3x+ F 4x
ku n është numri i termave të vektorëve. Projeksionet e tyre hyjnë në ekuacionin e mësipërm me shenjën përkatëse.
Në një plan, shuma gjeometrike e forcave mund të projektohet në dy akse koordinative, dhe në hapësirë, përkatësisht, në tre.
Do të ketë edhe detyra për një zgjidhje të pavarur, për të cilat mund të shihni përgjigjet.
Koncepti i vektorit
Përpara se të mësoni gjithçka rreth vektorëve dhe veprimeve mbi to, akordoni për të zgjidhur një problem të thjeshtë. Ekziston një vektor i ndërmarrjes suaj dhe një vektor i aftësive tuaja inovative. Vektori i sipërmarrjes të çon te qëllimi 1, dhe vektori i aftësive inovative - te qëllimi 2. Rregullat e lojës janë të tilla që nuk mund të lëvizësh në drejtimet e këtyre dy vektorëve njëherësh dhe të arrish dy qëllime njëherësh. Vektorët ndërveprojnë, ose, duke folur matematikisht, disa operacione kryhen në vektorë. Rezultati i këtij operacioni është vektori "Rezultati", i cili ju çon te Objektivi 3.
Tani më thuaj: rezultati i cilit operacion në vektorët "Ndërmarrja" dhe "Aftësitë inovative" është vektori "Rezultati"? Nëse nuk mund ta thoni menjëherë, mos u dekurajoni. Ndërsa studioni këtë mësim, do të jeni në gjendje t'i përgjigjeni kësaj pyetjeje.
Siç e kemi parë më lart, vektori domosdoshmërisht vjen nga një pikë A në një vijë të drejtë deri në një pikë B. Rrjedhimisht, çdo vektor ka jo vetëm një vlerë numerike - gjatësi, por edhe një drejtim fizik dhe gjeometrik. Nga kjo rrjedh përkufizimi i parë, më i thjeshtë i një vektori. Pra, një vektor është një segment i drejtuar që shkon nga një pikë A drejt e në temë B. Është shënuar kështu:

Dhe për të filluar ndryshe operacionet vektoriale , duhet të njihemi me një përkufizim tjetër të vektorit.
Një vektor është një lloj paraqitjeje e një pike që arrihet nga një pikënisje. Për shembull, një vektor tredimensional zakonisht shkruhet si (x, y, z) . E thënë thjesht, këta numra përfaqësojnë sa larg duhet të shkoni në tre drejtime të ndryshme për të arritur në pikën.
Le të jepet një vektor. ku x = 3 (dora e djathtë tregon djathtas) y = 1 (dora e majtë tregon përpara) z = 5 (nën pikën ka një shkallë që çon lart). Nga këto të dhëna, pikën do ta gjeni duke ecur 3 metra në drejtimin e treguar nga dora e djathtë, më pas 1 metër në drejtimin e treguar nga dora e majtë dhe më pas ju pret një shkallë dhe, duke u ngjitur 5 metra, më në fund do të gjeni veten në pikën e fundit.
Të gjithë termat e tjerë janë përsosje të shpjegimit të paraqitur më sipër, të nevojshme për veprime të ndryshme në vektorë, domethënë për zgjidhjen e problemeve praktike. Le të kalojmë nëpër këto përkufizime më rigoroze, duke u ndalur në problemet tipike vektoriale.
Shembuj fizikë Madhësitë vektoriale mund të jenë zhvendosja e një pike materiale që lëviz në hapësirë, shpejtësia dhe nxitimi i kësaj pike, si dhe forca që vepron në të.

vektor gjeometrik të përfaqësuar në hapësirë dydimensionale dhe tredimensionale në formë segment i drejtuar. Ky është një segment që ka një fillim dhe një fund.
Nese nje Aështë fillimi i vektorit, dhe Bështë fundi i tij, atëherë vektori shënohet me simbolin ose një shkronjë të vetme të vogël. Në figurë, fundi i vektorit tregohet me një shigjetë (Fig. 1)
Gjatësia(ose modul) e një vektori gjeometrik është gjatësia e segmentit që e gjeneron atë
Të dy vektorët quhen të barabartë , nëse mund të kombinohen (kur drejtimet përkojnë) me përkthim paralel, d.m.th. nëse janë paralele, drejtojeni në të njëjtin drejtim dhe kanë gjatësi të barabarta.
Në fizikë, shpesh konsiderohet vektorë të fiksuar, dhënë nga pika e aplikimit, gjatësia dhe drejtimi. Nëse pika e aplikimit të vektorit nuk ka rëndësi, atëherë ai mund të transferohet, duke mbajtur gjatësinë dhe drejtimin në çdo pikë të hapësirës. Në këtë rast, vektori quhet falas. Ne pranojmë të marrim parasysh vetëm vektorë të lirë.
Veprime lineare në vektorë gjeometrikë

Shumëzoni një vektor me një numër
Produkt vektorial për numër Një vektor quhet një vektor që përftohet nga një vektor duke u shtrirë (në ) ose duke u tkurrur (në ) herë, dhe drejtimi i vektorit ruhet nëse , dhe kthehet i kundërt nëse . (Fig. 2)
Nga përkufizimi del se vektorët dhe = janë gjithmonë të vendosur në një ose paralele. Vektorë të tillë quhen kolineare. (Mund të thuash gjithashtu se këta vektorë janë paralelë, por në algjebër vektoriale është zakon të thuhet "kolinear".) E kundërta është gjithashtu e vërtetë: nëse vektorët dhe janë kolinear, atëherë ato lidhen me relacionin
Prandaj, barazia (1) shpreh kushtin e kolinearitetit të dy vektorëve.

Mbledhja dhe zbritja e vektorit
Kur shtoni vektorë, duhet ta dini këtë shuma vektorë dhe quhet vektor, fillimi i të cilit përkon me fillimin e vektorit, dhe fundi - me fundin e vektorit, me kusht që fillimi i vektorit t'i bashkëngjitet fundit të vektorit. (Fig. 3)

Ky përkufizim mund të shpërndahet mbi çdo numër të kufizuar vektorësh. Lëreni në hapësirën e dhënë n vektorë të lirë. Kur mblidhen disa vektorë, shuma e tyre merret si vektor mbyllës, fillimi i të cilit përkon me fillimin e vektorit të parë dhe fundi me fundin e vektorit të fundit. Kjo do të thotë, nëse fillimi i vektorit është i bashkangjitur në fund të vektorit, dhe fillimi i vektorit në fund të vektorit, etj. dhe, së fundi, deri në fund të vektorit - fillimi i vektorit, atëherë shuma e këtyre vektorëve është vektori mbyllës ![]() , fillimi i të cilit përkon me fillimin e vektorit të parë dhe fundi i të cilit përkon me fundin e vektorit të fundit . (Fig. 4)
, fillimi i të cilit përkon me fillimin e vektorit të parë dhe fundi i të cilit përkon me fundin e vektorit të fundit . (Fig. 4)
Termat quhen komponentë të vektorit, dhe rregulli i formuluar është rregulli i shumëkëndëshit. Ky shumëkëndësh mund të mos jetë i sheshtë.
Kur një vektor shumëzohet me numrin -1, fitohet vektori i kundërt. Vektorët dhe kanë të njëjtën gjatësi dhe drejtime të kundërta. Shuma e tyre jep vektor zero, gjatësia e të cilit është zero. Drejtimi i vektorit null nuk është i përcaktuar.
Në algjebrën vektoriale, nuk ka nevojë të merret parasysh veçmas veprimi i zbritjes: të zbresësh një vektor nga një vektor do të thotë të shtosh vektorin e kundërt në vektor, d.m.th. ![]()
Shembulli 1 Thjeshtoni shprehjen:
![]() .
.
 ,
,
domethënë, vektorët mund të shtohen dhe të shumëzohen me numra në të njëjtën mënyrë si polinomet (në veçanti, edhe problemet për thjeshtimin e shprehjeve). Zakonisht, nevoja për të thjeshtuar shprehjet lineare të ngjashme me vektorë lind para llogaritjes së produkteve të vektorëve.
Shembulli 2 Vektorët dhe shërbejnë si diagonale të paralelogramit ABCD (Fig. 4a). Shprehni në terma dhe vektorët , , dhe , të cilët janë brinjët e këtij paralelogrami.

Zgjidhje. Pika e kryqëzimit të diagonaleve të një paralelogrami përgjysmon secilën diagonale. Gjatësitë e vektorëve që kërkohen në kushtin e problemit gjenden ose si gjysma e shumave të vektorëve që formojnë një trekëndësh me ata të dëshiruar, ose sa gjysma e diferencave (në varësi të drejtimit të vektorit që shërben si diagonale). ose, si në rastin e fundit, gjysma e shumës së marrë me shenjën minus. Rezultati janë vektorët e kërkuar në gjendjen e problemit:

Ka çdo arsye për të besuar se ju tani i jeni përgjigjur saktë pyetjes në lidhje me vektorët "Ndërmarrja" dhe "Aftësitë inovative" në fillim të këtij mësimi. Përgjigja e saktë: këta vektorë i nënshtrohen një operacioni të mbledhjes.
Zgjidhini vetë problemet në vektorë dhe më pas shikoni zgjidhjet
Si të gjeni gjatësinë e shumës së vektorëve?
Ky problem zë një vend të veçantë në veprimet me vektorë, pasi përfshin përdorimin e vetive trigonometrike. Le të themi se keni një detyrë si më poshtë:
Duke pasur parasysh gjatësinë e vektorëve ![]() dhe gjatësia e shumës së këtyre vektorëve . Gjeni gjatësinë e diferencës së këtyre vektorëve.
dhe gjatësia e shumës së këtyre vektorëve . Gjeni gjatësinë e diferencës së këtyre vektorëve.
Zgjidhje për këtë dhe probleme të tjera të ngjashme dhe shpjegime se si t'i zgjidhni ato - në mësim " Mbledhja e vektorit: gjatësia e shumës së vektorëve dhe teorema e kosinusit ".
Dhe ju mund të kontrolloni zgjidhjen e problemeve të tilla në Llogaritësi në internet "Ana e panjohur e një trekëndëshi (mbledhja e vektorit dhe teorema e kosinusit)" .
Ku janë prodhimet e vektorëve?
Prodhimet e një vektori nga një vektor nuk janë operacione lineare dhe konsiderohen veçmas. Dhe ne kemi mësimet "Produkti me pika i vektorëve" dhe "Produkti vektorial dhe i përzier i vektorëve".
Projeksioni i një vektori mbi një bosht
Projeksioni i një vektori në një bosht është i barabartë me produktin e gjatësisë së vektorit të projektuar dhe kosinusit të këndit midis vektorit dhe boshtit:
![]()
Siç dihet, projeksioni i një pike A në vijë (rrafsh) është baza e pingulit të rënë nga kjo pikë në vijë (rrafsh).

Le të - një vektor arbitrar (Fig. 5), dhe dhe - projeksionet e fillimit të tij (pikat A) dhe fundi (pikat B) për bosht l. (Për të ndërtuar projeksionin e një pike A) vizatoni drejt përmes pikës A rrafshi pingul me drejtëzën. Kryqëzimi i një linje dhe një rrafshi do të përcaktojë projeksionin e kërkuar.
Komponenti i vektorit në boshtin l quhet një vektor i tillë që shtrihet në këtë bosht, fillimi i të cilit përkon me projeksionin e fillimit, dhe fundi - me projeksionin e fundit të vektorit.
Projeksioni i vektorit në bosht l thirri një numër
![]() ,
,
e barabartë me gjatësinë e vektorit përbërës në këtë bosht, marrë me një shenjë plus nëse drejtimi i komponentit përkon me drejtimin e boshtit l, dhe me shenjën minus nëse këto drejtime janë të kundërta.
Karakteristikat kryesore të projeksioneve vektoriale në bosht:
1. Projeksionet e vektorëve të barabartë në të njëjtin bosht janë të barabartë me njëri-tjetrin.
2. Kur një vektor shumëzohet me një numër, projeksioni i tij shumëzohet me të njëjtin numër.
3. Projeksioni i shumës së vektorëve në çdo bosht është i barabartë me shumën e projeksioneve në të njëjtin bosht të termave të vektorëve.
4. Projeksioni i një vektori mbi një bosht është i barabartë me produktin e gjatësisë së vektorit të projektuar dhe kosinusit të këndit midis vektorit dhe boshtit:
![]()
 .
.

Zgjidhje. Le të projektojmë vektorët në bosht l siç përcaktohet në referencën teorike të mësipërme. Nga Fig.5a shihet qartë se projeksioni i shumës së vektorëve është i barabartë me shumën e projeksioneve të vektorëve. Ne llogarisim këto parashikime:

Gjejmë projeksionin përfundimtar të shumës së vektorëve:
Marrëdhënia e një vektori me një sistem koordinativ kartezian drejtkëndor në hapësirë
Njohja me Sistemi i koordinatave karteziane drejtkëndëshe në hapësirë u zhvillua në mësimin përkatës, mundësisht hapeni në një dritare të re.
Në një sistem të renditur të boshteve koordinative 0xyz boshti kau thirrur boshti x, boshti 0v – boshti y, dhe boshti 0z – boshti i aplikimit.

me pikë arbitrare M vektori i lidhjes hapësinore
thirrur vektori i rrezes pikë M dhe projektojeni atë në secilin prej boshteve koordinative. Le të shënojmë vlerat e projeksioneve përkatëse:
Numrat x, y, z thirrur koordinatat e pikës M, respektivisht abshissa, ordinator dhe aplikim, dhe shkruhen si një pikë e renditur numrash: M(x; y; z)(Fig. 6).
Një vektor me gjatësi njësi, drejtimi i të cilit përkon me drejtimin e boshtit quhet vektor njësi(ose ortom) sëpata. Shënoni me
Prandaj, vektorët njësi të boshteve të koordinatave kau, Oy, Oz
![]()
Teorema.Çdo vektor mund të zbërthehet në vektorët njësi të boshteve të koordinatave:

![]() (2)
(2)
Barazia (2) quhet zgjerimi i vektorit përgjatë boshteve koordinative. Koeficientët e këtij zgjerimi janë projeksionet e vektorit mbi boshtet koordinative. Kështu, koeficientët e zgjerimit (2) të vektorit përgjatë boshteve të koordinatave janë koordinatat e vektorit.
Pas zgjedhjes së një sistemi të caktuar koordinativ në hapësirë, vektori dhe trefishi i koordinatave të tij përcaktojnë në mënyrë unike njëri-tjetrin, kështu që vektori mund të shkruhet në formën
Paraqitjet vektoriale në formën (2) dhe (3) janë identike.
Gjendja e vektorëve kolinearë në koordinata
Siç e kemi vërejtur tashmë, vektorët quhen kolinearë nëse janë të lidhur nga relacioni
Le të vektorëve ![]() . Këta vektorë janë kolinearë nëse koordinatat e vektorëve lidhen me relacionin
. Këta vektorë janë kolinearë nëse koordinatat e vektorëve lidhen me relacionin
![]() ,
,
pra koordinatat e vektorëve janë proporcionale.
Shembulli 6 Vektorët e dhënë ![]() . A janë këta vektorë kolinear?
. A janë këta vektorë kolinear?
Zgjidhje. Le të zbulojmë raportin e koordinatave të këtyre vektorëve:
![]() .
.
Koordinatat e vektorëve janë proporcionale, prandaj, vektorët janë kolinearë, ose, çfarë është e njëjta, paralele.
Kosinuset e gjatësisë dhe drejtimit të vektorit
Për shkak të pingulitetit të ndërsjellë të boshteve të koordinatave, gjatësia e vektorit
![]()
është e barabartë me gjatësinë e diagonales së një paralelepipedi drejtkëndor të ndërtuar mbi vektorët
dhe shprehet me barazinë
![]() (4)
(4)
Një vektor përcaktohet plotësisht duke specifikuar dy pika (fillimi dhe fundi), kështu që koordinatat e vektorit mund të shprehen në terma të koordinatave të këtyre pikave.
Le të jetë fillimi i vektorit në sistemin e dhënë të koordinatave në pikën
dhe fundi është në pikën


Nga barazia
E ndjek atë
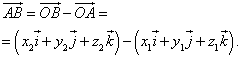
ose në formë koordinative
Rrjedhimisht, koordinatat e vektorit janë të barabarta me ndryshimet e koordinatave me të njëjtin emër të fundit dhe fillimit të vektorit . Formula (4) në këtë rast merr formën
Përcaktohet drejtimi i vektorit kosinuset e drejtimit . Këto janë kosinuset e këndeve që vektori bën me boshtet kau, Oy dhe Oz. Le t'i caktojmë këto kënde përkatësisht α , β dhe γ . Pastaj kosinuset e këtyre këndeve mund të gjenden me formula
Kosinuset e drejtimit të një vektori janë gjithashtu koordinatat e vektorit të vektorit dhe kështu vektori i vektorit

![]() .
.
Duke marrë parasysh se gjatësia e vektorit vektor është e barabartë me një njësi, d.m.th.
![]() ,
,
marrim barazinë e mëposhtme për kosinuset e drejtimit:
Shembulli 7 Gjeni gjatësinë e një vektori x = (3; 0; 4).
Zgjidhje. Gjatësia e vektorit është
![]()
Shembulli 8 Pikat e dhëna:
Zbuloni nëse trekëndëshi i ndërtuar në këto pika është dykëndësh.
Zgjidhje. Duke përdorur formulën e gjatësisë së vektorit (6), gjejmë gjatësitë e brinjëve dhe zbulojmë nëse dy prej tyre janë të barabarta:

Janë gjetur dy brinjë të barabarta, kështu që nuk ka nevojë të kërkohet gjatësia e brinjës së tretë dhe trekëndëshi i dhënë është dykëndësh.
Shembulli 9 Gjeni gjatësinë e një vektori dhe kosinuset e drejtimit të tij nëse ![]() .
.
Zgjidhje. Jepen koordinatat e vektorit:
![]() .
.
Gjatësia e vektorit është e barabartë me rrënjën katrore të shumës së katrorëve të koordinatave të vektorit:
![]() .
.
Gjetja e kosinuseve të drejtimit:

Zgjidheni vetë problemin e vektorëve dhe më pas shikoni zgjidhjen
Veprimet mbi vektorët e dhënë në formë koordinative
Le të jepen dy vektorë dhe të dhënë nga projeksionet e tyre:
![]()
![]()
Le të tregojmë veprimet në këta vektorë.
§ 3. Projeksionet vektoriale në boshtet koordinative1. Gjetja e projeksioneve gjeometrikisht.
Vektor
- projeksioni i vektorit mbi bosht OK
- projeksioni i vektorit mbi bosht OY
Përkufizimi 1. Projeksioni vektorial në çdo bosht koordinativ quhet një numër i marrë me shenjën "plus" ose "minus", që i përgjigjet gjatësisë së segmentit që ndodhet midis bazave të pinguleve, i ulur nga fillimi dhe fundi i vektorit deri në boshtin koordinativ.
Shenja e projeksionit përcaktohet si më poshtë. Nëse, kur lëvizni përgjatë boshtit të koordinatave, ka një lëvizje nga pika e projektimit të fillimit të vektorit në pikën e projektimit të fundit të vektorit në drejtimin pozitiv të boshtit, atëherë projeksioni i vektorit konsiderohet pozitiv. . Nëse - është e kundërt me boshtin, atëherë projeksioni konsiderohet negativ.

Figura tregon se nëse vektori është disi i orientuar përballë boshtit koordinativ, atëherë projeksioni i tij në këtë bosht është negativ. Nëse vektori është i orientuar disi në drejtimin pozitiv të boshtit të koordinatave, atëherë projeksioni i tij në këtë bosht është pozitiv.

Nëse vektori është pingul me boshtin koordinativ, atëherë projeksioni i tij në këtë bosht është i barabartë me zero.
Nëse një vektor është i bashkëdrejtuar me një bosht, atëherë projeksioni i tij në këtë bosht është i barabartë me modulin e vektorit.
Nëse vektori është i kundërt me boshtin koordinativ, atëherë projeksioni i tij në këtë bosht është i barabartë në vlerë absolute me modulin e vektorit, i marrë me shenjën minus.
2. Përkufizimi më i përgjithshëm i një projeksioni.

Nga një trekëndësh kënddrejtë ABD:.
Përkufizimi 2. Projeksioni vektorial në çdo bosht koordinativ quhet një numër i barabartë me prodhimin e modulit të vektorit dhe kosinusit të këndit të formuar nga vektori me drejtim pozitiv të boshtit koordinativ.

Shenja e projeksionit përcaktohet nga shenja e kosinusit të këndit të formuar nga vektori me drejtim pozitiv të boshtit.
Nëse këndi është akut, atëherë kosinusi ka një shenjë pozitive, dhe projeksionet janë pozitive. Për këndet e mpirë, kosinusi ka një shenjë negative, kështu që në raste të tilla projeksionet në bosht janë negative. ![]() - pra për vektorët pingul me boshtin, projeksioni është zero.
- pra për vektorët pingul me boshtin, projeksioni është zero.