është i diferencueshëm në intervalin (a, b). Pastaj ka një tangjente me grafikun e funksionit në çdo pikë 
kjo grafik ( 
), dhe tangjentja nuk është paralele me boshtin OY, pasi koeficienti këndor i saj është i barabartë me 
, sigurisht.
vendosmëri
në (a, b) ka një lëshim të drejtuar poshtë (lart) nëse ndodhet jo më e ulët (jo më e lartë) se çdo tangjente ndaj grafikut të funksionit në (a, b). 
(
) në të gjitha pikat e këtij intervali, atëherë kurba që është grafiku i funksionit është konveks (konkave) në këtë interval.
quhet pika e lakimit të grafikut të një funksioni nëse në pikë 
grafiku ka një tangjente, dhe ka një fqinjësi të tillë të pikës 
, brenda të cilit grafiku i funksionit majtas dhe djathtas të pikës ka drejtime të ndryshme konveksiteti.
Është e qartë se në pikën e lakimit tangjentja kryqëzon grafikun e funksionit, pasi në njërën anë të kësaj pike grafiku shtrihet mbi tangjenten, dhe nga ana tjetër - nën të, d.m.th., në afërsi të pikës së lakimit grafiku i funksionit kalon gjeometrikisht nga njëra anë e tangjentes në tjetrën dhe "përkulet" mbi të. Nga këtu vjen emri "pika e përkuljes".
derivat i dytë i vazhdueshëm. Pastaj 
.
nuk ka një pikë lakimi në (0, 0), megjithëse 
në 
. Prandaj, barazia e derivatit të dytë me zero është vetëm një kusht i domosdoshëm për lakimin. 
ka shenja të ndryshme majtas dhe djathtas të pikës, atëherë grafiku ka një lakim në pikë. 
ka një derivat të dytë në një lagje të pikës, me përjashtim të vetë pikës, dhe ka një tangjente me grafikun e funksionit në pikën 
. Pastaj, nëse brenda lagjes së specifikuar ka shenja të ndryshme majtas dhe djathtas të pikës, atëherë grafiku i funksionit ka një lakim në pikë. 
për konveksitetin, konkavitetin, pikat e lakimit. 
, 
=
nuk ekziston kur 
)
)
ose pranë pikave të ndërprerjes së llojit të 2-të, shpesh rezulton se grafiku i një funksioni i afrohet çdo linje të caktuar aq afër sa të dëshirohet. Këto quhen vija të drejta.
përkufizimi 1.
quhet asimptotë e një lakore L nëse distanca nga një pikë e kurbës në këtë drejtëz tenton në zero ndërsa pika largohet përgjatë kurbës deri në pafundësi. Ekzistojnë tre lloje asimptotash: vertikale, horizontale, të zhdrejtë. 
quhet asimptotë vertikale e grafikut të një funksioni nëse të paktën njëri nga kufijtë e njëanshëm është i barabartë me 
, dmth ose 
ka një asimptotë vertikale 
, sepse 
, A 
.
Nëse 
.
.
(
) quhet asimptota e pjerrët e grafikut të funksionit në 
Nëse 
; 
.
; x=0 – asimptotë vertikale
.
- asimptotë e zhdrejtë. 
dhe komplotoni atë. 
funksioni nuk është as çift dhe as tek-
-
+
+
y
-4
t r.
0
konkluzioni.
Një tipar i rëndësishëm i metodës së konsideruar është se ajo bazohet kryesisht në zbulimin dhe studimin e veçorive karakteristike në sjelljen e kurbës. Vendet ku funksioni ndryshon pa probleme nuk studiohen në detaje dhe nuk ka nevojë për një studim të tillë. Por ato vende ku funksioni ka ndonjë veçori në sjellje i nënshtrohen hulumtimit të plotë dhe paraqitjes më të saktë grafike. Këto veçori janë pikat maksimale, minimale, pikat e ndërprerjes së funksionit etj.
Përcaktimi i drejtimit të konkavitetit dhe lakimeve, si dhe metoda e specifikuar e gjetjes së asimptotave, bëjnë të mundur studimin e funksioneve edhe më në detaje dhe marrjen e një ideje më të saktë të grafikëve të tyre.
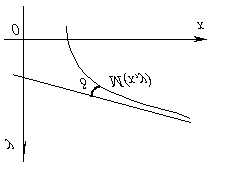
Grafiku i një funksioni y=f(x) thirrur konveks në intervalin (a; b), nëse ndodhet poshtë ndonjë tangjente të tij në këtë interval.
Grafiku i një funksioni y=f(x) thirrur konkave në intervalin (a; b), nëse ndodhet mbi ndonjë nga tangjentet e tij në këtë interval.
Figura tregon një kurbë që është konveks në (a; b) dhe konkave në (b;c).
Shembuj.
Le të shqyrtojmë një kriter të mjaftueshëm që na lejon të përcaktojmë nëse grafiku i një funksioni në një interval të caktuar do të jetë konveks ose konkav.
Teorema. Le y=f(x) i diferencueshëm nga (a; b). Nëse në të gjitha pikat e intervalit (a; b) derivati i dytë i funksionit y = f(x) negative, d.m.th. f ""(x) < 0, то график функции на этом интервале выпуклый, если же f""(x) > 0 – konkave.
Dëshmi. Le të supozojmë për saktësi se f""(x) < 0 и докажем, что график функции будет выпуклым.
Le të marrim funksionet në grafik y = f(x) pikë arbitrare M0 me abshisë x 0 Î ( a; b) dhe vizatoni pikën M0 tangjente. Ekuacioni i saj. Duhet të tregojmë se grafiku i funksionit në (a; b) shtrihet poshtë kësaj tangjente, d.m.th. me të njëjtën vlerë x ordinata e kurbës y = f(x) do të jetë më e vogël se ordinata e tangjentes.
Pra, ekuacioni i kurbës është y = f(x). Le të shënojmë ordinatën e tangjentes që i përgjigjet abshisë x. Pastaj . Rrjedhimisht, ndryshimi midis ordinatave të kurbës dhe tangjentes për të njëjtën vlerë x do .
Diferenca f(x) – f(x 0) transformimi sipas teoremës së Lagranzhit, ku c ndërmjet x Dhe x 0.
Kështu,
Zbatojmë përsëri teoremën e Lagranzhit për shprehjen në kllapa katrore: , ku c 1 ndërmjet c 0 Dhe x 0. Sipas kushteve të teoremës f ""(x) < 0. Определим знак произведения второго и третьего сомножителей.
Kështu, çdo pikë në kurbë shtrihet nën tangjenten e kurbës për të gjitha vlerat x Dhe x 0 Î ( a; b), që do të thotë se kurba është konvekse. Pjesa e dytë e teoremës vërtetohet në mënyrë të ngjashme.
Shembuj.
Pika në grafikun e një funksioni të vazhdueshëm që ndan pjesën e tij konveks nga pjesa konkave quhet pika e lakimit.
Natyrisht, në pikën e lakimit, tangjentja, nëse ekziston, e pret kurbën, sepse në njërën anë të kësaj pike kurba shtrihet nën tangjenten, dhe në anën tjetër - mbi të.
Le të përcaktojmë kushte të mjaftueshme për faktin se një pikë e caktuar e lakores është një pikë lakimi.
Teorema. Lëreni kurbën të përcaktohet nga ekuacioni y = f(x). Nëse f ""(x 0) = 0 ose f ""(x 0) nuk ekziston edhe kur kalon nëpër vlerë x = x 0 derivatore f ""(x) ndryshon shenjën, pastaj pikën në grafikun e funksionit me abshisën x = x 0 ka një pikë përkuljeje.
Dëshmi. Le f ""(x) < 0 при x < x 0 Dhe f ""(x) > 0 në x > x 0. Pastaj në x < x 0 kurba është konvekse, dhe kur x > x 0– konkave. Prandaj, pika A, i shtrirë në kurbë, me abshisë x 0 ka një pikë përkuljeje. Rasti i dytë mund të konsiderohet në mënyrë të ngjashme, kur f ""(x) > 0 në x < x 0 Dhe f ""(x) < 0 при x > x 0.
Kështu, pikat e lakimit duhet të kërkohen vetëm midis atyre pikave ku derivati i dytë zhduket ose nuk ekziston.
Shembuj. Gjeni pikat e lakimit dhe përcaktoni intervalet e konveksitetit dhe konkavitetit të kthesave.
ASIMPTOTAT E GRAFIT TË FUNKSIONIT
Kur studioni një funksion, është e rëndësishme të vendosni formën e grafikut të tij në një distancë të pakufizuar të pikës së grafikut nga origjina.
Me interes të veçantë është rasti kur grafiku i një funksioni, kur pika e tij e ndryshueshme hiqet në pafundësi, i afrohet pafundësisht një drejtëze të caktuar.
Vija e drejtë quhet asimptotë grafika e funksionit y = f(x), nëse distanca nga pika e ndryshueshme M grafika në këtë linjë kur hiqni një pikë M në pafundësi priret në zero, d.m.th. një pikë në grafikun e një funksioni, meqë priret drejt pafundësisë, duhet t'i afrohet pafundësisht asimptotës.
Një kurbë mund t'i afrohet asimptotës së saj, duke qëndruar në njërën anë të saj ose në anët e ndryshme, duke kaluar asimptotën një numër të pafundëm herë dhe duke lëvizur nga njëra anë në tjetrën.
Nëse shënojmë me d largësinë nga pika M kurbës në asimptotë, atëherë është e qartë se d tenton në zero ndërsa pika largohet M deri në pafundësi.
Më tej do të dallojmë asimptotën vertikale dhe atë të zhdrejtë.
ASIMPTOTA VERTIKALE
Le në x→ x 0 nga çdo funksion anësor y = f(x) rritet pafundësisht në vlerë absolute, d.m.th. ose ose 
. Pastaj nga përkufizimi i një asimptote del se drejtëza x = x 0është një asimptotë. E kundërta është gjithashtu e dukshme, nëse linja x = x 0është një asimptotë, d.m.th. .
Kështu, asimptota vertikale e grafikut të funksionit y = f(x) quhet drejtëz nëse f(x)→ ∞ në të paktën një nga kushtet x→ x 0- 0 ose x → x 0 + 0, x = x 0
Prandaj, për të gjetur asimptotat vertikale të grafikut të funksionit y = f(x) duhet gjetur ato vlera x = x 0, në të cilën funksioni shkon në pafundësi (pëson një ndërprerje të pafundme). Atëherë asimptota vertikale ka ekuacionin x = x 0.
Shembuj.
ASIMPTOTAT E PJERRËSISË
Meqenëse asimptota është një vijë e drejtë, atëherë nëse kurba y = f(x) ka një asimptotë të zhdrejtë, atëherë ekuacioni i tij do të jetë y = kx + b. Detyra jonë është të gjejmë koeficientët k Dhe b.
Teorema. Drejt y = kx + b shërben si asimptotë e zhdrejtë në x→ +∞ për grafikun e funksionit y
= f(x) atëherë dhe vetëm kur 
. Një deklaratë e ngjashme është e vërtetë për x → –∞.
Dëshmi. Le deputet– gjatësia e një segmenti të barabartë me distancën nga pika M për të asimptotuar. Sipas kushtit. Le të shënojmë me φ këndin e prirjes së asimptotës ndaj boshtit kau. Pastaj nga ΔMNP rrjedh se . Meqenëse φ është një kënd konstant (φ ≠ π/2), atëherë, por
Udhëzimet
Pikat e lakimit të një funksioni duhet t'i përkasin domenit të përkufizimit të tij, i cili duhet të gjendet së pari. Grafiku i një funksioni është një vijë që mund të jetë e vazhdueshme ose të ketë ndërprerje, të ulet ose rritet në mënyrë monotone, të ketë pika minimale ose maksimale (asimptota), të jetë konveks ose konkave. Një ndryshim i mprehtë në dy gjendjet e fundit quhet pikë e përkuljes.
Një kusht i domosdoshëm për ekzistencën e një lakimi të një funksioni është që i dyti të jetë i barabartë me zero. Kështu, duke e diferencuar funksionin dy herë dhe duke barazuar shprehjen që rezulton me zero, mund të gjejmë abshisën e pikave të mundshme të lakimit.
Ky kusht rrjedh nga përcaktimi i vetive të konveksitetit dhe konkavitetit të grafikut të një funksioni, d.m.th. vlerat negative dhe pozitive të derivatit të dytë. Në pikën e lakimit ka një ndryshim të mprehtë në këto veti, që do të thotë se derivati kalon shenjën zero. Megjithatë, e barabartë me zero nuk është ende e mjaftueshme për të treguar një lakim.
Ka dy kushte të mjaftueshme për faktin që abshisa e gjetur në fazën e mëparshme i përket pikës së lakimit: Nëpërmjet kësaj pike mund të vizatohet një tangjente me funksionin. Derivati i dytë ka shenja të ndryshme në të djathtë dhe në të majtë të pikës së supozuar të lakimit. Pra, ekzistenca e tij në pikën në vetvete nuk është e nevojshme, mjafton të përcaktohet se në të ajo ndryshon shenjën. Derivati i dytë i funksionit është i barabartë me zero, por i treti nuk është.
Kushti i parë i mjaftueshëm është universal dhe përdoret më shpesh se të tjerët. Shqyrtoni një shembull ilustrues: y = (3 x + 3) ∛(x - 5).
Zgjidhja: Gjeni domenin e përkufizimit. Në këtë rast nuk ka kufizime, prandaj është e gjithë hapësira e numrave realë. Llogaritni derivatin e parë: y’ = 3 ∛(x - 5) + (3 x + 3)/∛(x - 5)².
Vini re pamjen e thyesës. Nga kjo rezulton se fusha e përkufizimit të derivatit është e kufizuar. Pika x = 5 është e shpuar, që do të thotë se një tangjente mund të kalojë nëpër të, e cila pjesërisht i përgjigjet shenjës së parë të lakimit të mjaftueshëm.
Përcaktoni kufijtë e njëanshëm për shprehjen që rezulton për x → 5 – 0 dhe x → 5 + 0. Ata janë -∞ dhe +∞. Ju keni vërtetuar se një tangjente vertikale kalon në pikën x=5. Kjo pikë mund të jetë një pikë lakimi, por së pari llogaritni derivatin e dytë: Y'' = 1/∛(x - 5)² + 3/∛(x - 5)² – 2/3 (3 x + 3)/∛ (x - 5)^5 = (2 x – 22)/∛(x - 5)^5.
Hiqni emëruesin pasi tashmë keni marrë parasysh pikën x = 5. Zgjidheni ekuacionin 2 x – 22 = 0. Ai ka një rrënjë të vetme x = 11. Hapi i fundit është të konfirmoni që pikat x = 5 dhe x = 11 janë pika lakimi. Analizoni sjelljen e derivatit të dytë në afërsi të tyre. Natyrisht, në pikën x = 5 ndryshon shenjën nga "+" në "-", dhe në pikën x = 11 - anasjelltas. Përfundim: të dyja pikat janë pika lakimi. Kushti i parë i mjaftueshëm plotësohet.
Duke përdorur një kalkulator në internet mund të gjeni pikat e lakimit dhe intervalet e konveksitetit të grafikut të funksionit me hartimin e zgjidhjes në Word. Nëse një funksion i dy ndryshoreve f(x1,x2) është konveks, vendoset duke përdorur matricën Hessian.
Rregullat për futjen e funksioneve:
Drejtimi i konveksitetit të grafikut të një funksioni. Pikat e lakimit
Përkufizim: Lakorja y=f(x) quhet konvekse poshtë në intervalin (a; b) nëse shtrihet mbi tangjenten në çdo pikë të këtij intervali.Përkufizimi: Lakorja y=f(x) thuhet se është konvekse lart në intervalin (a; b) nëse shtrihet nën tangjenten në çdo pikë të këtij intervali. 
Përkufizim: Intervalet në të cilat grafiku i një funksioni është konveks lart ose poshtë quhen intervale të konveksitetit të grafikut të funksionit.
Konveksiteti poshtë ose lart i një lakore që është grafik i funksionit y=f(x) karakterizohet nga shenja e derivatit të dytë të saj: nëse në një interval të caktuar f''(x) > 0, atëherë kurba është konvekse. në rënie në këtë interval; nëse f''(x)< 0, то кривая выпукла вверх на этом промежутке.
Përkufizim: Pika në grafikun e funksionit y=f(x) që ndan intervalet e konveksitetit të drejtimeve të kundërta të këtij grafiku quhet pika e lakimit. 
Vetëm pikat kritike të llojit të dytë mund të shërbejnë si pika lakimi, d.m.th. pikat që i përkasin fushës së përkufizimit të funksionit y = f(x) në të cilin derivati i dytë f’’(x) zhduket ose ka një ndërprerje.
Rregulli për gjetjen e pikave të lakimit në grafikun e një funksioni y = f(x)
- Gjeni derivatin e dytë f’’(x) .
- Gjeni pikat kritike të llojit të dytë të funksionit y=f(x), d.m.th. pika në të cilën f''(x) zhduket ose përjeton një ndërprerje.
- Hulumtoni shenjën e derivatit të dytë f’’(x) në intervalin në të cilin pikat kritike të gjetura ndajnë domenin e përkufizimit të funksionit f(x). Nëse pika kritike x 0 ndan intervalet e konveksitetit të drejtimeve të kundërta, atëherë x 0 është abshisa e pikës së lakimit të grafikut të funksionit.
- Llogaritni vlerat e funksionit në pikat e lakimit.
Shembulli 1. Gjeni intervalet e konveksitetit dhe pikat e lakimit të lakores së mëposhtme: f(x) = 6x 2 –x 3.
Zgjidhje: Gjeni f ‘(x) = 12x – 3x 2 , f ‘’(x) = 12 – 6x.
Le të gjejmë pikat kritike të derivatit të dytë duke zgjidhur ekuacionin 12-6x=0. x=2. 
f(2) = 6*2 2 – 2 3 = 16
Përgjigje: Funksioni është konveks lart për x∈(2; +∞) ; funksioni është konveks poshtë në x∈(-∞; 2) ; pika e lakimit (2;16) .
Shembulli 2. A ka funksioni pika lakimi: f(x)=x 3 -6x 2 +2x-1
Shembulli 3. Gjeni intervalet ku grafiku i funksionit është konveks dhe i lakuar: f(x)=x 3 -6x 2 +12x+4
Për të përcaktuar konveksitetin (konkavitetin) e një funksioni në një interval të caktuar, mund të përdorni teoremat e mëposhtme.
Teorema 1. Le të jetë funksioni i përcaktuar dhe i vazhdueshëm në interval dhe të ketë një derivat të fundëm. Që një funksion të jetë konveks (konkav) në , është e nevojshme dhe e mjaftueshme që derivati i tij të zvogëlohet (rritet) në këtë interval.
Teorema 2. Le të jetë funksioni i përcaktuar dhe i vazhdueshëm së bashku me derivatin e tij në dhe të ketë një derivat të dytë të vazhdueshëm brenda. Për konveksitetin (konkavitetin) e një funksioni në të është e nevojshme dhe e mjaftueshme që brenda
Le të vërtetojmë teoremën 2 për rastin e funksionit konveks.
Domosdoshmëri. Le të marrim një pikë arbitrare. Le ta zgjerojmë funksionin rreth një pike në një seri Taylor
Ekuacioni i një tangjente me një kurbë në një pikë që ka një abshisë:
Atëherë teprica e kurbës mbi tangjenten me të në pikë është e barabartë me
Kështu, pjesa e mbetur është e barabartë me sasinë e tepricës së kurbës mbi tangjenten me të në pikën . Për shkak të vazhdimësisë, nëse 
, pastaj edhe për , që i përket një lagjeje mjaft të vogël të pikës , dhe për rrjedhojë, padyshim, për çdo vlerë të ndryshme nga , që i përket lagjes së treguar.
Kjo do të thotë që grafiku i funksionit qëndron mbi tangjenten dhe kurba është konvekse në një pikë arbitrare.
Përshtatshmëria. Lëreni kurbën të jetë konvekse në interval. Le të marrim një pikë arbitrare.
Ngjashëm me atë të mëparshëm, ne zgjerojmë funksionin rreth një pike në një seri Taylor
Teprica e kurbës mbi tangjenten me të në një pikë që ka një abshisë të përcaktuar nga shprehja është e barabartë me
Meqenëse teprica është pozitive për një lagje mjaftueshëm të vogël të pikës, derivati i dytë është gjithashtu pozitiv. Ndërsa përpiqemi, e gjejmë atë për një pikë arbitrare .
Shembull. Shqyrtoni funksionin për konveksitet (konkavitet).
Derivati i tij 
rritet në të gjithë vijën numerike, që do të thotë, nga teorema 1, funksioni është konkav në .
Derivati i dytë i tij 
, pra, nga teorema 2, funksioni është konkav në .
3.4.2.2 Pikat e lakimit
Përkufizimi. Pika e lakimit Grafiku i një funksioni të vazhdueshëm është pika që ndan intervalet në të cilat funksioni është konveks dhe konkav.
Nga ky përkufizim del se pikat e lakimit janë pikat ekstreme të derivatit të parë. Kjo nënkupton pohimet e mëposhtme për kushtet e nevojshme dhe të mjaftueshme për lakim.
Teorema (kushti i domosdoshëm për lakimin). Në mënyrë që një pikë të jetë një pikë lakimi e një funksioni dy herë të diferencueshëm, është e nevojshme që derivati i dytë i saj në këtë pikë të jetë i barabartë me zero ( 
) ose nuk ekzistonte.
Teorema (kusht i mjaftueshëm për lakim). Nëse derivati i dytë i një funksioni dy herë të diferencueshëm ndryshon shenjën kur kalon nëpër një pikë të caktuar, atëherë ka një pikë lakimi.
Vini re se në vetë pikën derivati i dytë mund të mos ekzistojë.
Interpretimi gjeometrik i pikave të përkuljes është ilustruar në Fig. 3.9
Në afërsi të një pike, funksioni është konveks dhe grafiku i tij shtrihet nën tangjentën e vizatuar në këtë pikë. Në afërsi të një pike, funksioni është konkav dhe grafiku i tij qëndron mbi tangjentën e vizatuar në këtë pikë. Në pikën e lakimit, tangjentja e ndan grafikun e funksionit në rajone konvekse dhe konkave.
3.4.2.3 Ekzaminimi i funksionit për konveksitetin dhe praninë e pikave të lakimit
1. Gjeni derivatin e dytë.
2. Gjeni pikat në të cilat derivati i dytë ose nuk ekziston.
Oriz. 3.9.
3. Hulumtoni shenjën e derivatit të dytë majtas dhe djathtas të pikave të gjetura dhe nxirrni një përfundim për intervalet e konveksitetit ose konkavitetit dhe pranisë së pikave të lakimit.
Shembull. Shqyrtoni funksionin për konveksitetin dhe praninë e pikave të lakimit.
2. Derivati i dytë është i barabartë me zero në .
3. Derivati i dytë ndryshon shenjën në , që do të thotë se pika është një pikë lakimi.
Në interval, atëherë funksioni është konveks në këtë interval.
Në intervalin , që do të thotë se funksioni është konkav në këtë interval.
3.4.2.4 Skema e përgjithshme për studimin e funksioneve dhe vizatimin e grafikut
Kur studioni një funksion dhe vizatoni grafikun e tij, rekomandohet të përdorni skemën e mëposhtme:
- Gjeni domenin e përkufizimit të funksionit.
- Hulumtoni funksionin për barazi - çuditshmëri. Kujtojmë se grafiku i një funksioni çift është simetrik në lidhje me boshtin e ordinatave, dhe grafiku i një funksioni tek është simetrik në lidhje me origjinën.
- Gjeni asimptota vertikale.
- Hetoni sjelljen e një funksioni në pafundësi, gjeni asimptota horizontale ose të zhdrejta.
- Gjeni ekstremet dhe intervalet e monotonitetit të funksionit.
- Gjeni intervalet e konveksitetit të funksionit dhe pikave të lakimit.
- Gjeni pikat e kryqëzimit me boshtet e koordinatave.
Studimi i funksionit kryhet njëkohësisht me ndërtimin e grafikut të tij.
Shembull. Funksioni i eksplorimit 
dhe komplotoni atë.
1. Domeni i funksionit është .
2. Funksioni në studim është i barabartë 
, prandaj grafiku i tij është simetrik ndaj ordinatës.
3. Emëruesi i funksionit shkon në zero në , kështu që grafiku i funksionit ka asimptota vertikale dhe .
Pikat janë pika ndërprerjeje të llojit të dytë, pasi kufijtë majtas dhe djathtas në këto pika priren të .
4. Sjellja e funksionit në pafundësi.
Prandaj, grafiku i funksionit ka një asimptotë horizontale.
5. Intervalet ekstreme dhe monotonike. Gjetja e derivatit të parë
Kur , pra, në këto intervale funksioni zvogëlohet.
Në , pra, në këto intervale funksioni rritet.
Në , prandaj pika është një pikë kritike.
Gjetja e derivatit të dytë
Meqenëse , atëherë pika është pika minimale e funksionit.
6. Intervalet e konveksitetit dhe pikat e lakimit.
Funksioni në 
, që do të thotë se funksioni është konkav në këtë interval.
Funksioni për , që do të thotë se funksioni është konveks në këto intervale.
Funksioni nuk zhduket askund, që do të thotë se nuk ka pika përkuljeje.
7. Pikat e kryqëzimit me boshtet koordinative.
Ekuacioni ka një zgjidhje, që nënkupton pikën e prerjes së grafikut të funksionit me boshtin e ordinatës (0, 1).
Ekuacioni nuk ka zgjidhje, që do të thotë se nuk ka pika të kryqëzimit me boshtin x.
Duke marrë parasysh hulumtimin e kryer, është e mundur të vizatohet funksioni
Grafiku skematik i një funksioni 
treguar në Fig. 3.10.
Oriz. 3.10.
3.4.2.5 Asimptotat e grafikut të një funksioni
Përkufizimi. Asimptotë Grafiku i një funksioni quhet një drejtëz që ka vetinë që distanca nga pika () në këtë drejtëz të priret në 0 ndërsa pika e grafikut lëviz pafundësisht nga origjina.
