10x − 5y − 3z = − 9,
6 x + 4 y − 5 z = − 1,3 x − 4 y − 6 z = − 23.
Le të barazojmë koeficientët për x në ekuacionin e parë dhe të dytë për ta bërë këtë, shumëzojmë të dy anët e ekuacionit të parë me 6, dhe të ekuacionit të dytë me 10, marrim:
60x − 30 y − 18z = − 54,60x + 40 y − 50z = − 10.
Ne zbresim ekuacionin e parë nga ekuacioni i dytë i sistemit që rezulton.
Prandaj, marrim: 70 y − 32 z = 44, 35 y − 16 z = 22.
Nga ekuacioni i dytë i sistemit origjinal zbresim ekuacionin e tretë të shumëzuar me 2, marrim: 4 y + 8 y − 5 z + 12 z = − 1 + 46,
12 y + 7z = 45.
Tani zgjidhim një sistem të ri ekuacionesh:
35y − 16z = 22.12y + 7z = 45.
Në ekuacionin e parë të sistemit të ri, shumëzuar me 7, shtojmë ekuacionin e dytë, shumëzuar me 16, marrim:
35 7 y + 12 16y = 22 7 + 45 16,
Tani ne zëvendësojmë y = 2, z = 3 në ekuacionin e parë të sistemit origjinal
tema, marrim: 10x − 5 2 − 3 3 = − 9, 10x − 10 − 9 = − 9, 10x = 10, x = 1.
Përgjigje: (1; 2; 3). ▲
§ 3. Zgjidhje sistemesh me parametra dhe me module
sëpatë + 4 y = 2 a,
Konsideroni sistemin e ekuacioneve
x + ay = a.

Viti akademik 2010-2011 viti, nr.3, klasa e 8-të. Matematika. Sistemet e ekuacioneve.
Në të vërtetë ekzistojnë tre variabla në këtë sistem, përkatësisht: a, x, y. x dhe y konsiderohen të panjohura, a quhet parametër. Kërkohet gjetja e zgjidhjeve (x, y) të këtij sistemi për çdo vlerë të parametrit a.
Le të tregojmë se si zgjidhen sisteme të tilla. Të shprehim ndryshoren x nga ekuacioni i dytë i sistemit: x = a − ay. Ne e zëvendësojmë këtë vlerë për x në ekuacionin e parë të sistemit, marrim:
a (a − ay) + 4 y = 2 a,
(2 − a )(2 + a ) y = a (2 − a ) .
Nëse a = 2, atëherë marrim ekuacionin 0 y = 0. Ky ekuacion plotësohet nga çdo numër y, dhe pastaj x = 2 − 2 y, d.m.th., për a = 2, çifti i numrave (2 − 2 y; y) është një zgjidhje për sistemin . Meqenëse mund të jeni
çdo numër, atëherë sistemi me a = 2 ka pafundësisht shumë zgjidhje.
Nëse a = − 2, atëherë marrim ekuacionin 0 y = 8. Ky ekuacion nuk ka zgjidhje.
Nëse tani një ≠ ± 2, |
atëherë y = |
a (2 − a) |
|||||||
(2 − a )(2 + a ) |
2+a |
||||||||
x = a − ay = a − |
|||||||||
2+a |
|||||||||
Përgjigje: Për a = 2, sistemi ka pafundësisht shumë zgjidhje të formës (2 − 2 y; y), ku y është çdo numër;
për a = − 2 sistemi nuk ka zgjidhje; |
||||||
për një ≠ ± 2, sistemi ka një zgjidhje unike |
. ▲ |
|||||
2+a |
2+a |
Ne e zgjidhëm këtë sistem dhe vendosëm se për cilat vlera të parametrit sistemi ka një zgjidhje, kur ka pafundësisht shumë zgjidhje dhe për cilat vlera të parametrit a nuk ka zgjidhje.
Shembulli 1: Zgjidheni sistemin e ekuacioneve
© 2010, FZFTSH në MIPT. Përpiluar nga: Yakovleva Tamara Kharitonovna

Viti akademik 2010-2011 viti, nr.3, klasa e 8-të. Matematika. Sistemet e ekuacioneve.
−3 |
y − 1 |
|||||||||||
3x − 2 y = 5. |
||||||||||||
Nga ekuacioni i dytë i sistemit që shprehim x me y, marrim |
||||||||||||
2 vj + 5 |
ne e zëvendësojmë këtë vlerë për x në ekuacionin e parë të sistemit |
|||||||||||
tema, marrim: |
2v + 5 |
−3 |
y − 1 |
−3 |
−1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5 = 0 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Shprehje |
y = − |
y > − |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
; Nëse |
−5 |
= −y |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Shprehja y − 1 = 0, |
nëse y = 1. Nëse |
y > 1, atëherë |
y − 1 |
Y − 1, dhe es- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
nëse y< 1, то |
y − 1 |
1 − y. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Nëse y ≥ 1, atëherë |
y − 1 |
Y−1 dhe |
marrim ekuacionin: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
−3 (v |
− 1) = 3, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
−3 y |
3, − |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(2 2 + |
5 ) = 3. Numri 2 > 1, pra çifti (3;2) është ri- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ndryshimi i sistemit. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lëreni tani |
5 ≤ y<1, |
y − 1 |
− y ; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
gjetjen |
marrim |
ekuacioni |
3y−3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4 vjeç + 10 |
3 y = 6, |
13 y = 8 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
© 2010, FZFTSH në MIPT. Përpiluar nga: Yakovleva Tamara Kharitonovna

Viti akademik 2010-2011 viti, nr.3, klasa e 8-të. Matematika. Sistemet e ekuacioneve.
(2 y + 5) = |
||||||||||||||||||||||||||||||
Por më pak se |
pra nja dy numra |
|||||||||||||||||||||||||||||
është një zgjidhje për sistemin. |
||||||||||||||||||||||||||||||
y< − |
atëherë marrim ekuacionin: |
3y−3 |
||||||||||||||||||||||||||||
4 y − |
3y = 6, |
5 y = |
28, y = 28. |
kuptimi |
||||||||||||||||||||||||||
pra nuk ka zgjidhje. |
||||||||||||||||||||||||||||||
Kështu, sistemi ka dy zgjidhje (3;2) dhe 13 27 ; 13 8 . ▲
§ 4. Zgjidhja e problemave duke përdorur sisteme ekuacionesh
Shembulli 1. Një makinë udhëton nga qyteti në fshat për 2,5 orë. Nëse e rrit shpejtësinë me 20 km/h, atëherë për 2 orë do të përshkojë një distancë prej 15 km më të madhe se distanca nga qyteti në fshat. Gjeni këtë distancë.
Le të shënojmë me S distancën midis qytetit dhe fshatit dhe me V shpejtësinë e makinës. Pastaj për të gjetur S fitojmë një sistem prej dy ekuacionesh
2.5V = S,
(V + 20) 2 = S + 15.
© 2010, FZFTSH në MIPT. Përpiluar nga: Yakovleva Tamara Kharitonovna

Viti akademik 2010-2011 viti, nr.3, klasa e 8-të. Matematika. Sistemet e ekuacioneve.
në ekuacionin e dytë: |
S + 20 2 |
S +15, |
S = 25, |
S = 125. |
||
Përgjigje: 125 km. ▲
Shembulli 2. Shuma e shifrave të një numri dyshifror është 15. Nëse këto shifra ndërrohen, ju merrni një numër që është 27 më shumë se origjinali. Gjeni këta numra.
Le të jetë numri i dhënë ab, d.m.th. numri i dhjetësheve është a, dhe numri i njësheve është b. Nga kushti i parë i problemës kemi: a + b = 15. Nëse e zbresim numrin ab nga numri ba, fitojmë 27, pra marrim ekuacionin e dytë: 10 b + a − (10 a + b) = 27. x
Viti akademik 2010-2011 viti, nr.3, klasa e 8-të. Matematika. Sistemet e ekuacioneve.
Le të shumëzojmë të dyja anët e ekuacionit me 20, marrim: x + 8 y = 840. Për të gjetur x dhe y marrim një sistem ekuacionesh
Përgjigje: 40 t, 100 t ▲
Shembulli 4. Një operator kompjuteri, duke punuar me një student, përpunon një detyrë në 2 orë 24 minuta. Nëse operatori punon për 2 orë, dhe studenti për 1 orë, atëherë
fëmijët përfunduan 2 3 të gjithë punës. Sa kohë do të duhet për të vepruar
ru dhe nxënësi veçmas për të përpunuar detyrën?
Le të shënojmë të gjithë punën me 1, produktivitetin e operatorit me x dhe produktivitetin e studentit me y. Ne e kemi parasysh atë
2 orë 24 minuta = 2 5 2 orë = 12 5 orë.
Nga kushti i parë i problemës del se (x+y) 12 5 = 1. Nga kushti i dytë i problemës del se 2 x + y = 2 3. Ne morëm një sistem ekuacionesh
(x+y) |
|||||||||||||||||||||||||||
2 x + y = |
|||||||||||||||||||||||||||
Ne e zgjidhim këtë sistem duke përdorur metodën e zëvendësimit: |
|||||||||||||||||||||||||||
− 2 x ; |
|||||||||||||||||||||||||||
−2x |
−x |
− 1; |
|||||||||||||||||||||||||
; x = |
; y = |
||||||||||||||||||||||||||
© 2010, FZFTSH në MIPT. Përpiluar nga: Yakovleva Tamara Kharitonovna
Prapa Përpara
Kujdes! Pamjet paraprake të diapozitivëve janë vetëm për qëllime informative dhe mund të mos përfaqësojnë të gjitha veçoritë e prezantimit. Nëse jeni të interesuar për këtë punë, ju lutemi shkarkoni versionin e plotë.
Qëllimi i mësimit. Zgjidhja e ekuacioneve me parametra dhe module, aplikimi i vetive të funksioneve në situata të papritura dhe zotërimi i teknikave gjeometrike për zgjidhjen e problemeve. Ekuacione jo standarde.
Detyrat:
- arsimore: të mësojë se si zgjidhen disa lloje ekuacionesh duke përdorur module dhe parametra;
- Zhvillimore: zhvilloni kulturën e të menduarit, kulturën e të folurit dhe aftësinë për të punuar me fletore dhe dërrasë të zezë.
- arsimore: kultivoni pavarësinë dhe aftësinë për të kapërcyer vështirësitë.
Pajisjet: material pamor për llogaritjen gojore dhe shpjegimin e një teme të re. Tabela e bardhë interaktive, pajisje multimediale mësimore.
Struktura e mësimit:
- Përsëritja e materialit të studiuar (numërimi me gojë).
- Mësimi i materialit të ri.
- Konsolidimi i materialit të studiuar.
- Përmbledhja e mësimit.
- Detyrë shtëpie.
PËRPARIMI I ORËS MËSIMORE
1. Përsëritja e materialit më të rëndësishëm teorik me temat: “Ekuacionet që përmbajnë një modul”, “Zgjidhja e ekuacioneve me parametra”
1) "Ekuacionet që përmbajnë një modul"
Vlera absolute ose moduli i një numri a është numri a, Nëse a> 0, numri - a, Nëse a < 0, нуль, если a= 0. Ose
Nga përkufizimi del se | a | >
0 dhe | a | >
a për të gjithë a€ R.
Pabarazia | x | < a, (Nëse a> 0) është ekuivalente me një pabarazi të dyfishtë - a <
X < a.
Pabarazia | x | < a, (Nëse a < 0)
не имеет смысла, так как | х | >0.
Pabarazia | x | > a, (Nëse a> 0) është ekuivalente me dy pabarazi
Pabarazia | x | > a, (Nëse a < 0)
справедливо для любого X€ R
2) "Zgjidhja e ekuacioneve me parametra"
Të zgjidhësh një ekuacion me parametra do të thotë të tregosh se në cilat vlera të parametrave ekzistojnë zgjidhjet dhe cilat janë ato.
a) të përcaktojë grupin e vlerave të pranueshme të të panjohurës dhe parametrave;
b) për çdo sistem të pranueshëm të vlerave të parametrave, gjeni grupet përkatëse të zgjidhjeve të ekuacionit.
2. Ushtrime me gojë
1. Zgjidh barazimin | x– 2 | = 5; Përgjigju: 7; – 3
| x– 2 | = – 5; Përgjigju: nuk ka zgjidhje
| x– 2 | = x + 5; Përgjigju: pa zgjidhje; 1.5
| x– 2 | = | x+ 5 |; Përgjigju: pa zgjidhje; – 1,5; nuk ka zgjidhje; – 1,5;
2. Zgjidh barazimin: | x+ 3 | + | y– 2 | = 4;
Le të shqyrtojmë katër raste
| { | x + 3 > 0 | { | x > – 3 |
| y – 2 > 0 | y > 2 | ||
| x + 3 + y – 2 = 4 | y = – x + 3 |
| { | x + 3 > 0 | { | x > – 3 |
| y – 2 < 0 | y < 2 | ||
| x + 3 – y + 2 = 4 | y = x + 1 |
| { | x + 3 < 0 | { | x < – 3 |
| y + 2 > 0 | y > – 2 | ||
| – x – 3 – y – 2 = 4 | y = x + 9 |
| { | x + 3 < 0 | { | x < – 3 |
| y + 2 < 0 | y < – 2 | ||
| – x – 3 – y – 2 = 4 | y = – x – 9 |

Si rezultat, marrim një katror, qendra e të cilit është (–3; 2), dhe gjatësia e diagonales është 8, dhe diagonalet janë paralele me boshtet e koordinatave.
Nga konsideratat vizuale mund të konkludojmë: se një ekuacion i formës | X + a | + | në + b | = Me; përcakton një katror në rrafsh me qendër në pikën (- A; – b), diagonalet paralele me boshtet OX dhe OU, dhe gjatësia e secilës diagonale është 2 Me. Përgjigju: (– 3; 2).
2. Zgjidheni ekuacionin aх = 1
Përgjigju: nëse a = 0, atëherë nuk ka zgjidhje; Nëse a= 0, atëherë X = 1/ a
3. Zgjidheni ekuacionin ( A 2 – 1) X = A + 1.
Zgjidhje.
Nuk është e vështirë të kuptohet se gjatë zgjidhjes së këtij ekuacioni mjafton të merren parasysh rastet e mëposhtme:
1) A= 1; atëherë ekuacioni merr formën OX = 2 dhe nuk ka zgjidhje
2) A= – 1; marrim OX = O, dhe padyshim X- ndonjë.
1
3) nëse A = +
1, atëherë X = –––
A
– 1
Përgjigje:
Nëse A= – 1, atëherë X- çdo;
Nëse A= 1, atëherë nuk ka zgjidhje;
1
Nëse A = +
1, atëherë X = –––
A
– 1

3. Zgjidhje për shembuj(nga opsionet C)
1. Në çfarë vlere të parametrit p bën ekuacioni | X 2 – 5X + 6 | + | X 2 – 5X + 4 | = r ka katër rrënjë.
Konsideroni funksionin y = | X 2 – 5X + 6 | + | X 2 – 5X + 4 |
Sepse X 2 – 5X + 6 = (X – 2)(X– 3) dhe X 2 – 5X + 4 = (X – 1)(X– 4), atëherë y = | (X – 2)(X – 3) | + | (X – 1)(X– 4) |, shënojmë rrënjët e trinomeve katrore në vijën numerike
1 2 3 4 X
Linja numerike është e ndarë në 5 intervale
| { | x < 1 | { | x < 1 |
| y = x 2 – 5x + 6 + x 2 – 5x + 4 | y = 2x 2 – 10x + 10 |
| { | 1 < x < 2 | { | 1 < x < 2 |
| y = x 2 – 5x+ 6 – x 2 + 5x – 4 | y = 2 |
| { | 2 < x < 3 | { | 2 < x <3 |
| y = – 2x 2 + 10x – 10 | y = – x 2 + 5x – 6 – x 2 + 5x – 4 |
| { | 3 < x < 4 | { | 3 < x < 4 |
| y = 2 | y = x 2 – 5x + 6 – x 2 + 5x – 4 |
| { | x > 4 | { | x > 4 |
| y = 2x 2 – 10x + 10 | y= x 2 – 5x + 6 + x 2 –5x + 4 |
Për rastin 3) X 0 = – b | 2a = 2, y 0 = 25: 2 + 25 – 10 = 2,5
Pra, (2.5; 2.5) janë koordinatat e kulmit të parabolës y = – 2x 2 + 10x – 10.
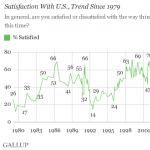
Le të ndërtojmë një grafik të funksionit të dhënë nga barazia

Siç shihet nga figura, ekuacioni origjinal ka katër rrënjë nëse 2 < A < 2,5
Përgjigju: në 2 < A < 2,5
4. Punë e pavarur në nivele
Niveli 1
1. Zgjidheni ekuacionin X 2 – | x| = 6
2. Për cilat vlera të plota të a-së ka një zgjidhje unike ekuacioni? Oh 2 – (A + 1) + A 2
+ A = 0?
Niveli 2
1. Zgjidh barazimin: | x – 5 | – | 2x + 3 | = 10
A –12) X 2 + 2 =
2(12 – A) ka dy rrënjë të ndryshme?
Niveli 3
1. Zgjidh barazimin | x – 5 | – | 2x + 3| = 10
2. Gjeni të gjitha vlerat e parametrit a për të cilin ekuacioni ( A – 12) X 2 + 2 = 2(12
– A) ka dy rrënjë të ndryshme?
5. Përmbledhje e mësimit
1. Përkufizimi i një moduli.
2. Çfarë do të thotë të zgjidhësh një ekuacion me një parametër?
6. Detyrë shtëpie. Opsioni C5 nr 11 F.F. Lysenko. Matematikë, 2012
1. Sistemet e ekuacioneve lineare me një parametër
Sistemet e ekuacioneve lineare me një parametër zgjidhen me të njëjtat metoda bazë si sistemet e zakonshme të ekuacioneve: metoda e zëvendësimit, metoda e shtimit të ekuacioneve dhe metoda grafike. Njohja e interpretimit grafik të sistemeve lineare e bën të lehtë përgjigjen e pyetjes për numrin e rrënjëve dhe ekzistencën e tyre.
Shembulli 1.
Gjeni të gjitha vlerat për parametrin a për të cilin sistemi i ekuacioneve nuk ka zgjidhje.
(x + (a 2 – 3)y = a,
(x + y = 2.
Zgjidhje.
Le të shohim disa mënyra për të zgjidhur këtë detyrë.
1 mënyrë. Ne përdorim vetinë: sistemi nuk ka zgjidhje nëse raporti i koeficientëve përballë x është i barabartë me raportin e koeficientëve përballë y, por jo i barabartë me raportin e termave të lirë (a/a 1 = b /b 1 ≠ c/c 1). Atëherë kemi:
1/1 = (a 2 – 3)/1 ≠ a/2 ose sistem
(dhe 2 - 3 = 1,
(a ≠ 2.
Nga ekuacioni i parë a 2 = 4, pra, duke marrë parasysh kushtin që a ≠ 2, marrim përgjigjen.
Përgjigje: a = -2.
Metoda 2. Ne zgjidhim me metodën e zëvendësimit.
(2 – y + (a 2 – 3) y = a,
(x = 2 - y,
((a 2 – 3) y – y = a – 2,
(x = 2 - y.
Pasi nxjerrim faktorin e përbashkët y nga kllapat në ekuacionin e parë, marrim:
((a 2 – 4)y = a – 2,
(x = 2 - y.
Sistemi nuk ka zgjidhje nëse ekuacioni i parë nuk ka zgjidhje, d.m.th
(dhe 2 - 4 = 0,
(a – 2 ≠ 0.
Natyrisht, a = ±2, por duke marrë parasysh kushtin e dytë, përgjigja vjen vetëm me një përgjigje minus.
Përgjigje: a = -2.
Shembulli 2.
Gjeni të gjitha vlerat për parametrin a për të cilin sistemi i ekuacioneve ka një numër të pafund zgjidhjesh.
(8x + ay = 2,
(sëpatë + 2y = 1.
Zgjidhje.
Sipas vetive, nëse raporti i koeficientëve të x dhe y është i njëjtë dhe është i barabartë me raportin e anëtarëve të lirë të sistemit, atëherë ai ka një numër të pafund zgjidhjesh (d.m.th. a/a 1 = b/ b 1 = c/c 1). Prandaj 8/a = a/2 = 2/1. Duke zgjidhur secilin prej ekuacioneve që rezultojnë, gjejmë se a = 4 është përgjigja në këtë shembull.
Përgjigje: a = 4.
2. Sistemet e ekuacioneve racionale me një parametër
Shembulli 3.
(3|x| + y = 2,
(|x| + 2y = a.
Zgjidhje.
Le të shumëzojmë ekuacionin e parë të sistemit me 2:
(6|x| + 2y = 4,
(|x| + 2y = a.
Duke zbritur ekuacionin e dytë nga i pari, marrim 5|x| = 4 – a. Ky ekuacion do të ketë një zgjidhje unike për a = 4. Në raste të tjera, ky ekuacion do të ketë dy zgjidhje (për një< 4) или ни одного (при а > 4).
Përgjigje: a = 4.
Shembulli 4.
Gjeni të gjitha vlerat e parametrit a për të cilat sistemi i ekuacioneve ka një zgjidhje unike.
(x + y = a,
(y – x 2 = 1.
Zgjidhje.
Ne do ta zgjidhim këtë sistem duke përdorur metodën grafike. Kështu, grafiku i ekuacionit të dytë të sistemit është një parabolë e ngritur përgjatë boshtit Oy lart me një segment njësi. Ekuacioni i parë specifikon një grup vijash paralele me drejtëzën y = -x (Figura 1). Nga figura shihet qartë se sistemi ka zgjidhje nëse drejtëza y = -x + a është tangjente me parabolën në një pikë me koordinata (-0.5, 1.25). Duke i zëvendësuar këto koordinata në ekuacionin e vijës së drejtë në vend të x dhe y, gjejmë vlerën e parametrit a: 
1,25 = 0,5 + a;
Përgjigje: a = 0,75.
Shembulli 5.
Duke përdorur metodën e zëvendësimit, zbuloni se në cilën vlerë të parametrit a, sistemi ka një zgjidhje unike.
(ax – y = a + 1,
(ax + (a + 2)y = 2.
Zgjidhje.
Nga ekuacioni i parë shprehim y dhe e zëvendësojmë me të dytin:
(y = sëpatë – a – 1,
(sëpatë + (a + 2) (sëpatë – a – 1) = 2.
Le ta reduktojmë ekuacionin e dytë në formën kx = b, i cili do të ketë një zgjidhje unike për k ≠ 0. Kemi:
sëpatë + a 2 x – a 2 – a + 2ax – 2a – 2 = 2;
a 2 x + 3ax = 2 + a 2 + 3a + 2.
Ne përfaqësojmë trinomin katror a 2 + 3a + 2 si produkt i kllapave
(a + 2) (a + 1), dhe në të majtë nxjerrim x nga kllapat:
(a 2 + 3a)x = 2 + (a + 2)(a + 1).
Natyrisht, një 2 + 3a nuk duhet të jetë e barabartë me zero, prandaj,
a 2 + 3a ≠ 0, a(a + 3) ≠ 0, që do të thotë a ≠ 0 dhe ≠ -3.
Përgjigje: a ≠ 0; ≠ -3.
Shembulli 6.
Duke përdorur metodën e zgjidhjes grafike, përcaktoni se në cilën vlerë të parametrit a sistemi ka një zgjidhje unike.
(x 2 + y 2 = 9,
(y – |x| = a.
Zgjidhje.
Në bazë të kushtit, ne ndërtojmë një rreth me qendër në origjinë dhe një rreze prej 3 segmentesh njësi, kjo është ajo që specifikohet nga ekuacioni i parë i sistemit
x 2 + y 2 = 9. Ekuacioni i dytë i sistemit (y = |x| + a) është një vijë e thyer. Duke përdorur figura 2 Ne i konsiderojmë të gjitha rastet e mundshme të vendndodhjes së tij në lidhje me rrethin. Është e lehtë të shihet se a = 3. 
Përgjigje: a = 3.
Ende keni pyetje? Nuk dini si të zgjidhni sistemet e ekuacioneve?
Për të marrë ndihmë nga një mësues -.
Mësimi i parë është falas!
blog.site, kur kopjoni materialin plotësisht ose pjesërisht, kërkohet një lidhje me burimin origjinal.
“Ekuacioni linear në dy variabla” - Një ekuacion që përmban dy ndryshore quhet ekuacion në dy ndryshore. -Si quhet një ekuacion me dy ndryshore? Jepni shembuj. -Cili ekuacion me dy ndryshore quhet linear? Ekuacion linear me dy ndryshore. Përkufizimi: Një algoritëm për të vërtetuar se një çift i caktuar numrash është një zgjidhje e ekuacionit:
"Zgjidhja e ekuacioneve eksponenciale" - Reduktimi në një bazë. Kllapa. T. Vieta. Metoda grafike. Një ekuacion eksponencial është një ekuacion që përmban një ndryshore me një eksponent. Zgjidhja e ekuacioneve eksponenciale. Punë gojore. ab+ac=a(b+c). Diplomat. 2.Zgjidhni ekuacionin: Veti. Llojet dhe metodat e zgjidhjes së ekuacioneve eksponenciale.
“Metodë grafike për zgjidhjen e ekuacioneve” - Përgjigje: një rrënjë, x = -1. Dy rrënjë. Të zgjidhet grafikisht ekuacioni (x+1)/(x-2)=2. Vizatoni një grafik të funksionit y=x?+6x+8. Punëtori për zgjidhjen grafike të ekuacioneve Përgatitja për testin. Ndërtoni grafikët e funksioneve. Grafikoni funksionin y=(x+1)/(x-2). 1. Zhvendoseni 8 në anën e djathtë të ekuacionit. Nuk ka rrënjë.
"Zgjidhja e ekuacioneve të tëra" - "Ekuacionet në të cilat ka rrënjë, shkallë dhe një humnerë pabarazish. Tre matematikanë të mëdhenj. Suksese në mësimin e mëtejshëm të metodave për zgjidhjen e ekuacioneve. Simetria boshtore është e natyrshme në shumicën e llojeve të bimëve dhe kafshëve. Qendrore. Ekzistojnë 2 lloje simetrie në botën e kafshëve. Diktim. Aksiale. Identifikoni metodat për zgjidhjen e ekuacioneve.
"Ekuacionet me logaritme" - Ekuacione logaritmike. Të zgjidhin ekuacionet me gojë. Formulat për konvertimin e logaritmeve. Ekuacioni. Përkufizimi. Tabelat e logaritmit. Përkufizimi i logaritmit. Përkufizimi dhe vetitë e logaritmit. Rregulli i rrëshqitjes. Funksioni. Kufje ose altoparlantë. Fusha e përkufizimit. Qasjet ndaj zgjidhjes. Zgjidhe ekuacionin. Gjimnazi.
“Ekuacionet irracionale” - Për qëllime kontrolli u plotësuan: Nr. 419 (c, d) Safiullina, Nr. 418 (c, d) Kulmukhametov, Nr. 420 (c, d) Shageev. Mësimi 2 Zgjidhja e sistemeve të ekuacioneve. Mësimi 1 Tema: Zgjidhja e ekuacioneve irracionale. 1.Cilët nga ekuacionet e mëposhtme janë irracionale: Objektivat: Të njohin nxënësit me zgjidhjet e disa llojeve të ekuacioneve irracionale.
Janë 49 prezantime gjithsej
Ruajtja e privatësisë suaj është e rëndësishme për ne. Për këtë arsye, ne kemi zhvilluar një politikë të privatësisë që përshkruan se si ne përdorim dhe ruajmë informacionin tuaj. Ju lutemi rishikoni praktikat tona të privatësisë dhe na tregoni nëse keni ndonjë pyetje.
Mbledhja dhe përdorimi i informacionit personal
Informacioni personal i referohet të dhënave që mund të përdoren për të identifikuar ose kontaktuar një person specifik.
Mund t'ju kërkohet të jepni informacionin tuaj personal në çdo kohë kur na kontaktoni.
Më poshtë janë disa shembuj të llojeve të informacionit personal që mund të mbledhim dhe se si mund ta përdorim këtë informacion.
Çfarë informacioni personal mbledhim:
- Kur dorëzoni një aplikim në sajt, ne mund të mbledhim informacione të ndryshme, duke përfshirë emrin tuaj, numrin e telefonit, adresën e emailit, etj.
Si i përdorim të dhënat tuaja personale:
- Informacioni personal që mbledhim na lejon t'ju kontaktojmë me oferta unike, promovime dhe ngjarje të tjera dhe ngjarje të ardhshme.
- Herë pas here, ne mund të përdorim të dhënat tuaja personale për të dërguar njoftime dhe komunikime të rëndësishme.
- Ne gjithashtu mund të përdorim të dhënat personale për qëllime të brendshme, si kryerja e auditimeve, analizave të të dhënave dhe kërkimeve të ndryshme, me qëllim që të përmirësojmë shërbimet që ofrojmë dhe t'ju ofrojmë rekomandime në lidhje me shërbimet tona.
- Nëse merrni pjesë në një tërheqje çmimesh, konkurs ose promovim të ngjashëm, ne mund të përdorim informacionin që ju jepni për të administruar programe të tilla.
Zbulimi i informacionit palëve të treta
Ne nuk ua zbulojmë informacionin e marrë nga ju palëve të treta.
Përjashtimet:
- Nëse është e nevojshme - në përputhje me ligjin, procedurën gjyqësore, në procedurat ligjore dhe/ose në bazë të kërkesave publike ose kërkesave nga autoritetet qeveritare në territorin e Federatës Ruse - për të zbuluar informacionin tuaj personal. Ne gjithashtu mund të zbulojmë informacione rreth jush nëse përcaktojmë se një zbulim i tillë është i nevojshëm ose i përshtatshëm për qëllime sigurie, zbatimi të ligjit ose qëllime të tjera me rëndësi publike.
- Në rast të një riorganizimi, bashkimi ose shitjeje, ne mund t'i transferojmë informacionet personale që mbledhim te pala e tretë pasardhëse e aplikueshme.
Mbrojtja e informacionit personal
Ne marrim masa paraprake - duke përfshirë administrative, teknike dhe fizike - për të mbrojtur informacionin tuaj personal nga humbja, vjedhja dhe keqpërdorimi, si dhe qasja, zbulimi, ndryshimi dhe shkatërrimi i paautorizuar.
Respektimi i privatësisë suaj në nivel kompanie
Për t'u siguruar që informacioni juaj personal është i sigurt, ne i komunikojmë punonjësve tanë standardet e privatësisë dhe sigurisë dhe zbatojmë në mënyrë rigoroze praktikat e privatësisë.