TEKSTI TRANSKRIPT I MËSIMIT:
Ideja e një aeroplani në hapësirë na lejon të marrim, për shembull, sipërfaqen e një tavoline ose muri. Megjithatë, një tavolinë ose mur ka përmasa të fundme, dhe rrafshi shtrihet përtej kufijve të tij deri në pafundësi.
Konsideroni dy plane të kryqëzuara. Kur kryqëzohen, formojnë katër kënde dykëndëshe me një skaj të përbashkët.
Le të kujtojmë se çfarë është një kënd dihedral.
Në realitet, hasim objekte që kanë formën e një këndi dykëndor: për shembull, një derë pak e hapur ose një dosje gjysmë të hapur.
Kur dy rrafshe alfa dhe beta ndërpriten, marrim katër kënde dykëndëshe. Le të jetë një nga këndet dihedral të barabartë me (phi), atëherë i dyti është i barabartë me (1800 -), i treti, i katërti (1800 -).
Shqyrtoni rastin kur njëri nga këndet dihedral është 900.
Atëherë, të gjitha këndet dihedrale në këtë rast janë të barabarta me 900.
Le të prezantojmë përkufizimin e rrafsheve pingule:
Dy plane quhen pingul nëse këndi dihedral ndërmjet tyre është 90°.
Këndi midis planeve sigma dhe epsilon është 90 gradë, që do të thotë se rrafshet janë pingul
Le të japim shembuj të planeve pingul.
Muri dhe tavani.

Muri anësor dhe pjesa e sipërme e tavolinës.
Le të formulojmë një shenjë të pingulitetit të dy planeve:
TEOREMA: Nëse njëri prej dy rrafsheve kalon nëpër një drejtëz pingul me rrafshin tjetër, atëherë këto plane janë pingul.
Le ta vërtetojmë këtë shenjë.
Sipas kushtit, dihet që drejtëza AM shtrihet në rrafshin α, drejtëza AM është pingul me rrafshin β,
Vërtetoni: rrafshet α dhe β janë pingul.
Dëshmi:
1) Planet α dhe β kryqëzohen përgjatë vijës së drejtë AR, ndërsa AM është AR, pasi AM është β sipas kushtit, domethënë AM është pingul me çdo vijë të drejtë që shtrihet në planin β.
2) Le të vizatojmë një vijë të drejtë AT pingul me AP në rrafshin β.
Marrim këndin TAM - këndin linear të këndit dihedral. Por këndi TAM = 90°, pasi MA është β. Pra α β.

Q.E.D.
Nga shenja e pingulitetit të dy rrafsheve kemi një përfundim të rëndësishëm:
KORROLLA: Një rrafsh pingul me një vijë përgjatë së cilës kryqëzohen dy rrafshe është pingul me secilin prej këtyre rrafsheve.
Kjo është: nëse α∩β=с dhe γ с, atëherë γ α dhe γ β.
Le të vërtetojmë këtë përfundim: nëse rrafshi i gama është pingul me drejtëzën c, atëherë, bazuar në paralelizmin e dy planeve, gama është pingul me alfa. Po kështu, gama është pingul me beta
Le ta riformulojmë këtë përfundim për një kënd dihedral:
Rrafshi që kalon nëpër këndin linear të një këndi dykëndor është pingul me skajin dhe faqet e këtij këndi dihedral. Me fjalë të tjera, nëse kemi ndërtuar një kënd linear të një këndi dykëndor, atëherë rrafshi që kalon nëpër të është pingul me skajin dhe faqet e këtij këndi dihedral.
Jepet: ΔABC, C = 90°, AC shtrihet në rrafshin α, këndi ndërmjet planeve α dhe ABC = 60°, AC = 5 cm, AB = 13 cm.
Gjeni: distancën nga pika B në rrafshin α.

1) Le të ndërtojmë VC α. Atëherë KS është projeksioni i diellit në këtë plan.
2) BC AC (sipas kushtit), që do të thotë, sipas teoremës së tre pingulave (TPP), KS AC. Prandaj, VSK është këndi linear i këndit dihedral ndërmjet rrafshit α dhe rrafshit të trekëndëshit ABC. Kjo është, VSK = 60 °.
3) Nga ΔBCA sipas teoremës së Pitagorës:
Përgjigja VK është e barabartë me 6 rrënjë prej tre cm
Përdorimi praktik (natyra e aplikuar) e pingulitetit të dy rrafsheve.
Dy drejtëza në hapësirë quhen pingul nëse këndi ndërmjet tyre është 90 o.
oriz. 37 |
Vijat pingule mund të kryqëzohen dhe mund të jenë të zhdrejtë. Lemë. Nëse njëra prej dy drejtëzave paralele është pingul me drejtëzën e tretë, atëherë drejtëza tjetër është pingul me këtë drejtëz. Përkufizimi. Një drejtëz quhet pingul me një rrafsh nëse është pingul me çdo drejtëz që shtrihet në rrafsh. Ata gjithashtu thonë se rrafshi është pingul me drejtëzën a. |
oriz. 38 |
Nëse drejtëza a është pingul me rrafshin, atëherë padyshim që e pret këtë rrafsh. Në fakt, nëse drejtëza a nuk e pret rrafshin, atëherë ajo do të shtrihej në këtë rrafsh ose do të ishte paralele me të. Por në të dyja rastet do të kishte drejtëza në rrafsh që nuk janë pingul me drejtëzën a, për shembull, drejtëza paralele me të, gjë që është e pamundur. Kjo do të thotë se drejtëza a e pret rrafshin. |
Marrëdhënia ndërmjet paralelizmit të drejtëzave dhe pingulitetit të tyre me rrafshin.
Shenja e pingulitetit të një drejtëze dhe një rrafshi.
Shënime.
- Përmes çdo pike të hapësirës kalon një plan pingul me një vijë të caktuar, dhe për më tepër, i vetmi.
- Përmes çdo pike të hapësirës kalon një vijë e drejtë pingul me një plan të caktuar, dhe vetëm një.
- Nëse dy plane janë pingul me një drejtëz, atëherë ato janë paralele.
Problema dhe teste me temën “Tema 5. “Perpendikulariteti i drejtëzës dhe rrafshit”.
- Perpendikulariteti i drejtëzës dhe rrafshit
- Këndi dihedral. Perpendikulariteti i planeve - Perpendikulariteti i vijave dhe planeve, shkalla 10
Mësime: 1 Detyra: 10 Teste: 1
- pingul dhe i zhdrejtë. Këndi ndërmjet vijës së drejtë dhe rrafshit - Perpendikulariteti i vijave dhe planeve, shkalla 10
Mësime: 2 Detyra: 10 Teste: 1
- Paralelizmi i drejtëzave, vijës dhe rrafshit - Paralelizmi i drejtëzave dhe planeve, klasa 10
Mësime: 1 Detyra: 9 Teste: 1
- Vija pingule - Informacion bazë gjeometrik klasa e 7-të
Mësime: 1 Detyra: 17 Teste: 1
Materiali mbi temën përmbledh dhe sistematizon informacionin që dini nga planimetria për pingulitetin e drejtëzave. Këshillohet që të kombinohet studimi i teoremave për marrëdhëniet ndërmjet paralelizmit dhe pingulitetit të drejtëzave dhe rrafsheve në hapësirë, si dhe materialit në pingul dhe të pjerrët, me një përsëritje sistematike të materialit përkatës nga planimetria.
Zgjidhjet për pothuajse të gjitha problemet e llogaritjes vijnë në zbatimin e teoremës së Pitagorës dhe pasojat e saj. Në shumë probleme, mundësia e përdorimit të teoremës së Pitagorës ose pasojave të saj justifikohet nga teorema e tre pingulave ose vetitë e paralelizmit dhe pingulitetit të planeve.
Koncepti i rrafsheve pingul
Kur dy plane kryqëzohen, marrim kënde dykëndëshe prej $4$. Dy kënde janë të barabarta me $\varphi $, dhe dy të tjerët janë të barabartë me $(180)^0-\varphi $.
Përkufizimi 1
Këndi ndërmjet rrafsheve është minimumi i këndeve dihedrale të formuara nga këto plane.
Përkufizimi 2
Dy plane të kryqëzuara quhen pingul nëse këndi ndërmjet këtyre planeve është $90^\circ$ (Fig. 1).
Figura 1. Planet pingul
Shenja e pingulitetit të dy planeve
Teorema 1
Nëse një vijë e drejtë e një rrafshi është pingul me një rrafsh tjetër, atëherë këto plane janë pingul me njëri-tjetrin.
Dëshmi.
Le të na jepen aeroplanët $\alpha $ dhe $\beta $, të cilët kryqëzohen përgjatë vijës së drejtë $AC$. Lëreni drejtëzën $AB$ që shtrihet në rrafshin $\alpha $ të jetë pingul me rrafshin $\beta $ (Fig. 2).

Figura 2.
Meqenëse drejtëza $AB$ është pingul me rrafshin $\beta$, ajo është gjithashtu pingul me vijën $AC$. Le të vizatojmë gjithashtu një vijë $AD$ në rrafshin $\beta$, pingul me vijën $AC$.
Ne gjejmë se këndi $BAD$ është këndi linear i këndit dihedral, i barabartë me $90^\circ$. Kjo do të thotë, sipas përkufizimit 1, këndi ndërmjet planeve është $90^\circ$, që do të thotë se këto plane janë pingul.
Teorema është vërtetuar.
Nga kjo teoremë rrjedh teorema e mëposhtme.
Teorema 2
Nëse një rrafsh është pingul me vijën përgjatë së cilës kryqëzohen dy plane të tjera, atëherë ai është gjithashtu pingul me këto plane.
Dëshmi.
Le të na jepen dy rrafshe $\alpha $ dhe $\beta $ që kryqëzohen përgjatë vijës së drejtë $c$. Rrafshi $\gamma $ është pingul me vijën e drejtë $c$ (Fig. 3)

Figura 3.
Meqenëse rreshti $c$ i përket rrafshit $\alpha $ dhe rrafshi $\gamma $ është pingul me vijën $c$, atëherë, sipas Teoremës 1, rrafshit $\alpha $ dhe $\gamma $ janë pingul.
Meqenëse rreshti $c$ i përket rrafshit $\beta $ dhe rrafshi $\gamma $ është pingul me vijën $c$, atëherë, sipas Teoremës 1, rrafshit $\beta $ dhe $\gamma $ janë pingul.
Teorema është vërtetuar.
Për secilën nga këto teorema, pohimet e kundërta janë gjithashtu të vërteta.
Shembuj të problemeve
Shembulli 1
Le të na jepet një paralelipiped drejtkëndor $ABCDA_1B_1C_1D_1$. Gjeni të gjitha çiftet e rrafsheve pingul (Fig. 5).
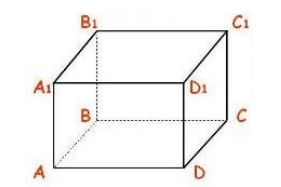
Figura 4.
Zgjidhje.
Sipas përcaktimit të një plani drejtkëndor paralelipiped dhe pingul, ne shohim tetë çiftet e mëposhtme të planeve pingul me njëri-tjetrin: $(ABB_1)$ dhe $(ADD_1)$, $(ABB_1)$ dhe $(A_1B_1C_1)$, $( ABB_1)$ dhe $(BCC_1) $, $(ABB_1)$ dhe $(ABC)$, $(DCC_1)$ dhe $(ADD_1)$, $(DCC_1)$ dhe $(A_1B_1C_1)$, $(DCC_1) $ dhe $(BCC_1)$, $(DCC_1)$ dhe $(ABC)$.
Shembulli 2
Le të na jepen dy rrafshe pingul reciprokisht. Nga një pikë në një rrafsh tërhiqet një pingul në një plan tjetër. Vërtetoni se kjo vijë shtrihet në rrafshin e dhënë.
Dëshmi.
Le të na jepen plane pingul $\alpha $ dhe $\beta $ që kryqëzohen përgjatë vijës së drejtë $c$. Nga pika $A$ e rrafshit $\beta $ një pingul $AC$ tërhiqet në rrafshin $\alfa $. Le të supozojmë se $AC$ nuk qëndron në rrafshin $\beta$ (Fig. 6).
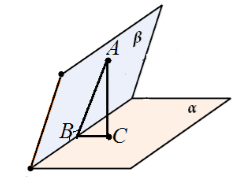
Figura 5.
Merrni parasysh trekëndëshin $ABC$. Është drejtkëndëshe me kënd të drejtë $ACB$. Prandaj, $\këndi ABC\ne (90)^0$.
Por nga ana tjetër, $\këndi ABC$ është këndi linear i këndit dihedral të formuar nga këto plane. Kjo do të thotë, këndi dihedral i formuar nga këto plane nuk është i barabartë me 90 gradë. Konstatojmë se këndi ndërmjet planeve nuk është i barabartë me 90$^\circ$. Kontradikta. Prandaj, $AC$ qëndron në planin $\beta$.
Ky mësim do t'i ndihmojë ata që dëshirojnë të kuptojnë temën "Shenja e pingulitetit të dy planeve". Në fillim të tij, ne do të përsërisim përkufizimin e këndeve dihedral dhe linear. Pastaj do të shqyrtojmë se cilët rrafshe quhen pingul dhe do të vërtetojmë shenjën e pingulitetit të dy rrafsheve.
Tema: Perpendikulariteti i drejtëzave dhe planeve
Mësimi: Shenja e pingulitetit të dy planeve
Përkufizimi. Një kënd dihedral është një figurë e formuar nga dy gjysmërrafshe që nuk i përkasin të njëjtit rrafsh dhe drejtëza e tyre e përbashkët a (a është një skaj).
Oriz. 1
Le të shqyrtojmë dy gjysmërrafshe α dhe β (Fig. 1). Kufiri i tyre i përbashkët është l. Kjo shifër quhet një kënd dihedral. Dy plane të kryqëzuara formojnë katër kënde dihedrale me një skaj të përbashkët.
Një kënd dihedral matet me këndin e tij linear. Ne zgjedhim një pikë arbitrare në skajin e përbashkët l të këndit dihedral. Në gjysmërrafshet α dhe β, nga kjo pikë vizatojmë pingulat a dhe b në drejtëzën l dhe fitojmë këndin linear të këndit dykëndor.
Vijat e drejta a dhe b formojnë katër kënde të barabarta me φ, 180° - φ, φ, 180° - φ. Kujtojmë se këndi ndërmjet vijave të drejta është më i vogli nga këto kënde.
Përkufizimi. Këndi ndërmjet rrafsheve është më i vogli nga këndet dihedrale të formuara nga këto rrafshe. φ është këndi ndërmjet planeve α dhe β, nëse
Përkufizimi. Dy plane të kryqëzuara quhen pingul (reciprokisht pingul) nëse këndi ndërmjet tyre është 90°.

Oriz. 2
Një pikë arbitrare M zgjidhet në skajin l (Fig. 2). Le të vizatojmë dy drejtëza pingule MA = a dhe MB = b në skajin l në rrafshin α dhe në rrafshin β, përkatësisht. Ne morëm këndin AMB. Këndi AMB është këndi linear i një këndi dihedral. Nëse këndi AMB është 90°, atëherë rrafshet α dhe β quhen pingul.
Drejtëza b është pingul me drejtëzën l nga ndërtimi. Drejtëza b është pingul me drejtëzën a, pasi këndi ndërmjet planeve α dhe β është 90°. Konstatojmë se drejtëza b është pingul me dy drejtëza a dhe l që ndërpriten nga rrafshi α. Kjo do të thotë se drejtëza b është pingul me rrafshin α.
Në mënyrë të ngjashme, mund të vërtetojmë se drejtëza a është pingul me rrafshin β. Drejtëza a është pingul me drejtëzën l nga ndërtimi. Drejtëza a është pingul me drejtëzën b, pasi këndi ndërmjet rrafsheve α dhe β është 90°. Konstatojmë se drejtëza a është pingul me dy drejtëza të prera b dhe l nga rrafshi β. Kjo do të thotë se drejtëza a është pingul me rrafshin β.
Nëse njëri prej dy rrafsheve kalon nëpër një drejtëz pingul me rrafshin tjetër, atëherë rrafshe të tillë janë pingul.
Provoni:

Oriz. 3
Dëshmi:
Le të ndërpriten rrafshet α dhe β përgjatë vijës së drejtë AC (Fig. 3). Për të vërtetuar se rrafshet janë pingul reciprokisht, duhet të ndërtoni një kënd linear midis tyre dhe të tregoni se ky kënd është 90°.
Drejtëza AB është pingul me rrafshin β, dhe për rrjedhojë me drejtëzën AC që shtrihet në rrafshin β.
Le të vizatojmë një drejtëz AD pingul me një drejtëz AC në rrafshin β. Atëherë BAD është këndi linear i këndit dihedral.
Drejtëza AB është pingul me rrafshin β, dhe për rrjedhojë me drejtëzën AD që shtrihet në rrafshin β. Kjo do të thotë se këndi linear BAD është 90°. Kjo do të thotë që rrafshet α dhe β janë pingul, gjë që duhej vërtetuar.
Rrafshi pingul me drejtëzën përgjatë së cilës kryqëzohen dy plane të dhëna është pingul me secilin prej këtyre rrafsheve (Fig. 4).
Provoni:

Oriz. 4
Dëshmi:
Drejtëza l është pingul me rrafshin γ, dhe rrafshi α kalon nëpër drejtëzën l. Kjo do të thotë se sipas pingulitetit të rrafsheve, rrafshet α dhe γ janë pingul.
Drejtëza l është pingul me rrafshin γ, dhe rrafshi β kalon nëpër drejtëzën l. Kjo do të thotë se sipas pingulitetit të planeve, rrafshet β dhe γ janë pingul.
Ligjëratë me temën “Testi i pingulitetit të dy planeve”
Ideja e një aeroplani në hapësirë na lejon të marrim, për shembull, sipërfaqen e një tavoline ose muri. Megjithatë, një tavolinë ose mur ka përmasa të fundme, dhe rrafshi shtrihet përtej kufijve të tij deri në pafundësi.Konsideroni dy plane të kryqëzuara. Kur kryqëzohen, formojnë katër kënde dykëndëshe me një skaj të përbashkët.
Le të kujtojmë se çfarë është një kënd dihedral.
Në realitet, hasim objekte që kanë formën e një këndi dykëndor: për shembull, një derë pak e hapur ose një dosje gjysmë të hapur.

Kur dy rrafshe alfa dhe beta ndërpriten, marrim katër kënde dykëndëshe. Le të jetë një nga këndet dihedral të barabartë me (phi), atëherë i dyti është i barabartë me (180 0 –), e treta, e katërta (180 0 -).

α Dheβ, 0°< 90 °
Shqyrtoni rastin kur një nga këndet dihedral është 90 0 .
Atëherë, të gjitha këndet dihedrale në këtë rast janë të barabarta me 90 0 .
këndi dihedral ndërmjet planeveα Dheβ,
90º
Le të prezantojmë përkufizimin e rrafsheve pingule:
Dy plane quhen pingul nëse këndi dihedral ndërmjet tyre është 90°.
Këndi midis planeve sigma dhe epsilon është 90 gradë, që do të thotë se rrafshet janë pingul
Sepse =90°
Le të japim shembuj të planeve pingul.
Muri dhe tavani.
Muri anësor dhe pjesa e sipërme e tavolinës.

Mur dhe tavan
Le të formulojmë një shenjë të pingulitetit të dy planeve:
TEOREMA:Nëse njëri prej dy rrafsheve kalon nëpër një drejtëz pingul me rrafshin tjetër, atëherë këto plane janë pingul.
Le ta vërtetojmë këtë shenjë.
Me kusht dihet se drejtëzaAM shtrihet në rrafshin α, drejtëza AM është pingul me rrafshin β,
Vërtetoni: rrafshet α dhe β janë pingul.
Dëshmi:
1) Planet α dheβ kryqëzohen përgjatë vijës së drejtë AR dhe AM AR, pasi AM β sipas kushtit, domethënë AM është pingul me çdo vijë të drejtë që shtrihet në rrafshin β.
2) Le të vizatojmë një vijë të drejtë në rrafshin βAT pingulAR.
Marrim këndin TAM është këndi linear i këndit dihedral. Por këndi TAM = 90°, pasi MA është β. Pra α β.
Q.E.D.
TEOREMA:Nëse një rrafsh kalon nëpër një drejtëz pingul me një rrafsh tjetër, atëherë këto plane janë pingul.

E dhënë:α, β, AM α, AMβ, AM∩=A
Vërtetoni: αβ.
Dëshmi:
1) α∩β = AR, ndërsa AM AR, pasi AM β sipas kushtit, domethënë AM është pingul me çdo vijë të drejtë që shtrihet në rrafshin β.
2) ATβ,ATAR.
TAM është këndi linear i këndit dihedral. TAM = 90°, sepse MA β. Pra α β.
Q.E.D
Nga shenja e pingulitetit të dy rrafsheve kemi një përfundim të rëndësishëm:
NDIKIMI:Një rrafsh pingul me një vijë përgjatë së cilës kryqëzohen dy plane është pingul me secilin prej këtyre rrafsheve.
Le të vërtetojmë këtë përfundim: nëse rrafshi i gama është pingul me drejtëzën c, atëherë, bazuar në paralelizmin e dy planeve, gama është pingul me alfa. Po kështu, gama është pingul me beta

Kjo është: nëse α∩β=с dhe γс, atëherë γα dhe γβ.
sepseγс dhe σα nga shenja e pingulitetit γα.
Ngjashëm me γ β
Le ta riformulojmë këtë përfundim për një kënd dihedral:
Rrafshi që kalon nëpër këndin linear të një këndi dykëndor është pingul me skajin dhe faqet e këtij këndi dihedral. Me fjalë të tjera, nëse kemi ndërtuar një kënd linear të një këndi dykëndor, atëherë rrafshi që kalon nëpër të është pingul me skajin dhe faqet e këtij këndi dihedral.

Detyrë.
Jepet: ΔАВС, С = 90°, АС shtrihet në rrafshin α, këndi ndërmjet rrafsheve α dheABC= 60°, AC = 5 cm, AB = 13 cm.
Gjeni: distancën nga pika B në rrafshin α.
Zgjidhja:
1) Le të ndërtojmë VC α. Atëherë KS është projeksioni i diellit në këtë plan.
2) BC AC (sipas kushtit), që do të thotë, sipas teoremës së tre pingulave (TPP), KS AC. Prandaj, VSK është këndi linear i këndit dihedral ndërmjet rrafshit α dhe rrafshit të trekëndëshit ABC. Kjo është, VSK = 60 °.
3) Nga ΔBCA sipas teoremës së Pitagorës:
Nga ΔVKS: ![]()