수직면의 표시 및 속성. "두 평면의 직각 기호"라는 주제로 수학을 강의합니다. 주제: 선과 평면의 수직성

수업 내용:

공간에 평면이 있다는 아이디어를 통해 예를 들어 테이블이나 벽의 표면을 얻을 수 있습니다. 그러나 테이블이나 벽은 유한한 크기를 가지며 평면은 경계를 넘어 무한대로 확장됩니다.

두 개의 교차 평면을 고려하십시오. 교차할 때 공통 모서리를 갖는 4개의 2면체 각도를 형성합니다.

2면각이 무엇인지 기억해 봅시다.

실제로 우리는 약간 열린 문이나 반쯤 열린 폴더와 같이 2면체 모양의 물체를 접하게 됩니다.

두 평면 알파와 베타가 교차하면 4개의 2면각을 얻습니다. 2면체 각도 중 하나를 (phi)와 같게 하고, 두 번째는 (1800-), 세 번째, 네 번째는 (1800-)과 같습니다.

2면각 중 하나가 900인 경우를 생각해 보세요.

그러면 이 경우 모든 2면각은 900과 같습니다.

수직 평면의 정의를 소개하겠습니다.

두 평면 사이의 이면각이 90°인 경우 두 평면을 수직이라고 합니다.

시그마 평면과 엡실론 평면 사이의 각도는 90도입니다. 이는 평면이 수직임을 의미합니다.

수직면의 예를 들어 보겠습니다.

벽과 천장.

측벽과 테이블 상판.

두 평면의 수직성 기호를 공식화해 보겠습니다.

정리: 두 평면 중 하나가 다른 평면에 수직인 선을 통과하면 두 평면은 수직입니다.

이 표시를 증명해 봅시다.

조건에 따라 직선 AM은 평면 α에 있고 직선 AM은 평면 β에 수직이라는 것이 알려져 있습니다.

증명: 평면 α와 β는 수직입니다.

증거:

1) 평면 α와 β는 직선 AR을 따라 교차하는 반면 AM은 조건에 따라 AM이 β이기 때문에 AM은 AR입니다. 즉, AM은 β 평면에 있는 모든 직선에 수직입니다.

2) β 평면에서 AP에 수직인 직선 AT를 그리자.

우리는 2면체 각도의 선형 각도인 TAM 각도를 얻습니다. 그러나 MA는 β이므로 각도 TAM = 90°입니다. 그러니까 αβ.

Q.E.D.

두 평면의 수직성의 부호로부터 우리는 중요한 결과를 얻습니다:

결과: 두 평면이 교차하는 선에 수직인 평면은 이들 평면 각각에 수직입니다.

즉, α∩β=с이고 γ с이면 γ α 및 γ β입니다.

이 결과를 증명해 보겠습니다. 감마 평면이 선 c에 수직이면 두 평면의 평행성에 기초하여 감마는 알파에 수직입니다. 마찬가지로 감마는 베타와 수직이다.

2면각에 대한 이 결과를 다시 공식화해 보겠습니다.

2면각의 선형 각도를 통과하는 평면은 이 2면각의 모서리와 면에 수직입니다. 즉, 2면각의 선형 각도를 구성한 경우 이를 통과하는 평면은 이 2면각의 모서리 및 면에 수직입니다.

주어진 값: ΔABC, C = 90°, AC는 α 평면에 있고, α 평면과 ABC 평면 사이의 각도 = 60°, AC = 5cm, AB = 13cm.

찾기: 점 B에서 평면 α까지의 거리.

1) VCα를 구성해보자. 그러면 KS는 이 평면에 태양을 투영하는 것입니다.

2) BC AC(조건별), 이는 세 수직의 정리(TPP)에 따라 KS AC를 의미합니다. 따라서 VSK는 평면 α와 삼각형 ABC의 평면 사이의 2면각의 선형 각도입니다. 즉, VSK = 60°입니다.

3) 피타고라스 정리에 따른 ΔBCA로부터:

답 VK는 3cm의 6뿌리와 같습니다.

두 평면의 직각도의 실제 사용(응용 특성)입니다.

공간에 있는 두 직선 사이의 각도가 90°이면 수직이라고 합니다.

쌀. 37

수직선은 교차할 수도 있고 기울어질 수도 있습니다.

보조정리.두 평행선 중 하나가 세 번째 선에 수직이면 다른 선도 이 선에 수직입니다.

정의.평면에 있는 임의의 선에 수직인 선을 평면에 수직이라고 합니다.

그들은 또한 평면이 선 a에 수직이라고 말합니다.

쌀. 38

선 a가 평면에 수직이면 분명히 이 평면과 교차합니다. 실제로 선 a가 평면과 교차하지 않으면 이 평면에 놓이거나 평행하게 됩니다.

그러나 두 경우 모두 평면에 선 a에 수직이 아닌 선, 예를 들어 a에 평행한 선이 있을 수 있으며 이는 불가능합니다. 이는 직선 a가 평면과 교차한다는 것을 의미합니다.

선의 평행성과 평면에 대한 수직성 사이의 관계.

선과 평면의 수직성을 나타내는 기호입니다.

메모.

공간의 모든 지점을 통과하면 주어진 선에 수직인 평면, 게다가 유일한 평면이 통과합니다.
공간의 모든 지점을 통과하면 주어진 평면에 수직인 직선이 하나만 통과합니다.
두 평면이 선에 수직이면 평행합니다.

"주제 5. "선과 평면의 수직성" 주제에 대한 문제 및 테스트입니다.

선과 평면의 수직성
이면체 각도. 평면의 직각성 - 선과 평면의 수직성, 10급
수업: 1 과제: 10 시험: 1
수직 및 비스듬함. 직선과 평면 사이의 각도 - 선과 평면의 수직성, 10급
수업: 2 과제: 10 시험: 1
직선, 선, 평면의 평행성 - 선과 평면의 평행성, 10급
수업: 1 과제: 9 시험: 1
수직선 - 기초기하정보 7급
수업: 1 과제: 17 시험: 1

주제에 대한 자료는 직선의 직각성에 대해 면적 측정을 통해 알고 있는 정보를 요약하고 체계화합니다. 공간의 직선과 평면, 수직 및 경사면의 재료의 평행성과 직각도 사이의 관계에 대한 정리 연구를 면적계의 해당 재료를 체계적으로 반복하는 것과 결합하는 것이 좋습니다.

거의 모든 계산 문제에 대한 해결책은 피타고라스 정리의 적용과 그 결과로 귀결됩니다. 많은 문제에서 피타고라스 정리 또는 그 결과를 사용할 가능성은 세 수직의 정리 또는 평면의 평행성과 수직성의 특성에 의해 정당화됩니다.

수직면의 개념

두 평면이 교차하면 $4$의 2면각을 얻습니다. 두 각도는 $\varphi $와 같고, 나머지 두 각도는 $(180)^0-\varphi $와 같습니다.

정의 1

평면 사이의 각도는 이들 평면에 의해 형성된 2면체 각도의 최소값입니다.

정의 2

두 평면 사이의 각도가 $90^\circ$이면 교차하는 두 평면을 수직이라고 합니다(그림 1).

그림 1. 수직면

두 평면의 직각도 표시

정리 1

한 평면의 직선이 다른 평면에 수직이면 두 평면도 서로 수직입니다.

증거.

직선 $AC$를 따라 교차하는 평면 $\alpha $와 $\beta $가 있다고 가정하겠습니다. $\alpha $ 평면에 있는 직선 $\beta $ 평면이 $\beta $ 평면에 수직이 되도록 합니다(그림 2).

그림 2.

$AB$ 선은 $\beta$ 평면에 수직이므로 $AC$ 선에도 수직입니다. $\beta$ 평면에 $AC$ 선에 수직인 $AD$ 선을 추가로 그려 보겠습니다.

우리는 각도 $BAD$가 $90^\circ$와 동일한 2면체 각도의 선형 각도라는 것을 알았습니다. 즉, 정의 1에 따르면 평면 사이의 각도는 $90^\circ$입니다. 이는 두 평면이 수직임을 의미합니다.

정리가 입증되었습니다.

이 정리에서 다음 정리가 나옵니다.

정리 2

한 평면이 다른 두 평면이 교차하는 선에 수직인 경우 해당 평면도 해당 평면에 수직입니다.

증거.

직선 $c$를 따라 교차하는 두 평면 $\alpha $ 및 $\beta $가 있다고 가정하겠습니다. 평면 $\gamma $는 직선 $c$에 수직입니다(그림 3).

그림 3.

$c$ 선은 $\alpha $ 평면에 속하고 $\gamma $ 평면은 $c$ 선에 수직이므로, 정리 1에 따르면 $\alpha $ 평면과 $\gamma $ 평면은 수직입니다.

$c$ 선은 $\beta $ 평면에 속하고 $\gamma $ 평면은 $c$ 선에 수직이므로, 정리 1에 따르면 $\beta $ 평면과 $\gamma $ 평면은 수직입니다.

정리가 입증되었습니다.

이러한 각 정리에 대해 반대의 진술도 참입니다.

샘플 문제

실시예 1

직육면체 $ABCDA_1B_1C_1D_1$가 있다고 가정하겠습니다. 수직면의 모든 쌍을 찾으십시오 (그림 5).

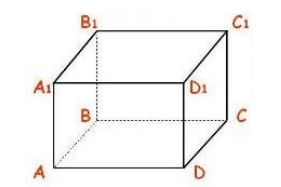
그림 4.

해결책.

직육면체 및 수직 평면의 정의에 따라 서로 수직인 다음 8쌍의 평면을 볼 수 있습니다: $(ABB_1)$ 및 $(ADD_1)$, $(ABB_1)$ 및 $(A_1B_1C_1)$, $( ABB_1)$ 및 $(BCC_1) $, $(ABB_1)$ 및 $(ABC)$, $(DCC_1)$ 및 $(ADD_1)$, $(DCC_1)$ 및 $(A_1B_1C_1)$, $(DCC_1) $ 및 $(BCC_1)$, $(DCC_1)$ 및 $(ABC)$.

실시예 2

서로 수직인 두 개의 평면이 있다고 가정해 보겠습니다. 한 평면의 한 점에서 다른 평면에 수직선이 그려집니다. 이 직선이 주어진 평면에 있음을 증명하십시오.

증거.

직선 $c$를 따라 교차하는 수직 평면 $\alpha $ 및 $\beta $가 있다고 가정하겠습니다. $\beta $ 평면의 $A$ 점에서 $\alpha $ 평면에 수직인 $AC$가 그려집니다. $AC$가 $\beta$ 평면에 있지 않다고 가정해 보겠습니다(그림 6).

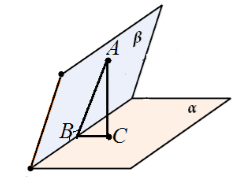
그림 5.

삼각형 $ABC$를 생각해 보세요. $ACB$가 직각인 직사각형입니다. 따라서 $\angle ABC\ne (90)^0$입니다.

그러나 반면 $\angle ABC$는 이들 평면에 의해 형성된 2면각의 선형 각도입니다. 즉, 이들 평면에 의해 형성된 이면각은 90도와 같지 않습니다. 우리는 평면 사이의 각도가 $90^\circ$와 같지 않다는 것을 발견했습니다. 모순. 따라서 $AC$는 $\beta$ 평면에 있습니다.

이 수업은 "두 평면의 수직 기호"라는 주제를 이해하려는 사람들에게 도움이 될 것입니다. 처음에는 2면체 각도와 선형 각도의 정의를 반복합니다. 그런 다음 어떤 평면을 수직이라고 부르는지 고려하고 두 평면의 직각 기호를 증명합니다.

주제: 선과 평면의 수직성

교훈: 두 평면의 직각 표시

정의. 2면각은 동일한 평면에 속하지 않는 두 개의 반평면과 공통 직선 a(a는 모서리)로 구성된 도형입니다.

쌀. 1

두 개의 반평면 α와 β를 고려해 보겠습니다(그림 1). 그들의 공통 경계는 l입니다. 이 그림을 2면각이라고 합니다. 두 개의 교차 평면은 공통 모서리를 갖는 4개의 2면체 각도를 형성합니다.

2면각은 선형 각도로 측정됩니다. 2면각의 공통 모서리 l에서 임의의 점을 선택합니다. 반면 α와 β에서, 이 지점에서 직선 l에 수직인 a와 b를 그리고 2면각의 선형 각도를 얻습니다.

직선 a와 b는 Ø, 180° - Ø, Ø, 180° - Ø와 같은 네 개의 각도를 형성합니다. 직선 사이의 각도는 이러한 각도 중 가장 작다는 것을 기억하십시오.

정의. 평면 사이의 각도는 이들 평면에 의해 형성된 2면체 각도 중 가장 작습니다. Φ는 평면 α와 β 사이의 각도입니다.

정의. 두 개의 교차하는 평면 사이의 각도가 90°인 경우 수직(상호 수직)이라고 합니다.

쌀. 2

임의의 점 M이 모서리 l에서 선택됩니다(그림 2). α 평면과 β 평면에서 모서리 l에 각각 두 개의 수직 직선 MA = a 및 MB = b를 그립니다. 우리는 AMB 각도를 얻었습니다. 각도 AMB는 2면각의 선형 각도입니다. 각도 AMB가 90°이면 평면 α와 β를 수직이라고 합니다.

선 b는 구조적으로 선 l에 수직입니다. 평면 α와 β 사이의 각도가 90°이므로 선 b는 선 a에 수직입니다. 우리는 선 b가 평면 α에서 교차하는 두 선 a와 l에 수직임을 알 수 있습니다. 이는 직선 b가 평면 α에 수직임을 의미합니다.

마찬가지로 직선 a가 평면 β에 수직임을 증명할 수 있습니다. 선 a는 구조적으로 선 l에 수직입니다. 평면 α와 β 사이의 각도가 90°이므로 선 a는 선 b에 수직입니다. 우리는 선 a가 평면 β에서 교차하는 두 선 b와 l에 수직임을 알 수 있습니다. 이는 직선 a가 평면 β에 수직이라는 것을 의미합니다.

두 평면 중 하나가 다른 평면에 수직인 선을 통과하면 해당 평면은 수직입니다.

입증하다: