je diferencibilan na intervalu (a, c). Tada postoji tangenta na graf funkcije u bilo kojoj točki 
ovaj graf ( 
), a tangenta nije paralelna s osi OY, budući da je njezin nagib jednak 
, naravno.
definicija
na (a, c) ima otpuštanje usmjereno prema dolje (gore) ako se ne nalazi ispod (ne iznad) bilo koje tangente na graf funkcije na (a, c). 
(
) u svim točkama ovog intervala, tada je krivulja koja je graf funkcije konveksna (konkavna) na tom intervalu.
naziva se točka pregiba grafa funkcije, ako je u točki 
graf ima tangentu i postoji takvo susjedstvo točke 
, unutar kojega graf funkcije lijevo i desno od točke ima različite smjerove konveksnosti.
očito je da u prijevojnoj točki tangenta prelazi preko grafa funkcije, budući da s jedne strane ove točke graf leži iznad tangente, a s druge - ispod nje, tj. u blizini točke pregiba, graf funkcije prolazi geometrijski s jedne strane tangente na drugu i "savija se" kroz nju. Odatle dolazi naziv "točka pregiba".
kontinuirani drugi izvod. Zatim 
.
iako nema točku pregiba na (0, 0). 
na 
. Stoga je jednakost druge derivacije nuli samo nužan uvjet za fleksiju. 
ima različite predznake lijevo i desno od točke, tada graf ima fleksiju u točki. 
ima drugu derivaciju u nekom susjedstvu točke, osim same točke, i postoji tangenta na graf funkcije u točki 
. Zatim, ako unutar naznačenog susjedstva ima različite predznake lijevo i desno od točke , tada graf funkcije ima infleksiju u točki . 
konveksnost, konkavnost, pregibne točke. 
, 
=
ne postoji kod 
)
)
ili blizu točaka diskontinuiteta 2. vrste, često se pokaže da se graf funkcije približava jednoj ili drugoj ravnoj liniji koliko god netko želi. Takve linije nazivaju se.
definicija 1.
naziva se asimptotom krivulje L ako udaljenost od točke krivulje do ove linije teži nuli dok se točka udaljava duž krivulje u beskonačnost. Postoje tri vrste asimptota: okomite, horizontalne, kose. 
naziva se vertikalna asimptota grafa funkcije ako je barem jedna od jednostranih granica jednaka 
, tj. ili 
ima vertikalnu asimptotu 
, jer 
, a 
.
ako 
.
.
(
) naziva se kosa asimptota grafa funkcije za 
ako 
; 
.
; x=0 – vertikalna asimptota
.
je kosa asimptota. 
i zacrtaj ga. 
ne funkcioniraju ni parne ni neparne-
-
+
+
y
-4
t r.
0
Zaključak.
Važna značajka razmatrane metode je da se temelji prvenstveno na otkrivanju i proučavanju karakterističnih značajki u ponašanju krivulje. Mjesta na kojima se funkcija glatko mijenja ne proučavaju se posebno detaljno i nema potrebe za takvim proučavanjem. Ali ona mjesta gdje funkcija ima bilo kakve osobitosti u ponašanju podliježu potpunom istraživanju i najtočnijem grafičkom prikazu. Ove značajke su točke maksimuma, minimuma, točke diskontinuiteta funkcije itd.
Određivanje smjera udubljenja i pregiba, kao i naznačena metoda pronalaženja asimptota, omogućuju još detaljnije proučavanje funkcija i točniju predodžbu o njihovim grafovima.
Grafikon funkcije y=f(x) pozvao konveksan na intervalu (a; b), ako se nalazi ispod bilo koje svoje tangente na ovom intervalu.
Grafikon funkcije y=f(x) pozvao konkavna na intervalu (a; b), ako se nalazi iznad bilo koje svoje tangente u ovom intervalu.
Slika prikazuje krivulju konveksnu na (a; b) i konkavno na (prije Krista).
Primjeri.
Uzmite u obzir dovoljan znak koji vam omogućuje da odredite hoće li graf funkcije u danom intervalu biti konveksan ili konkavan.
Teorema. Neka bude y=f(x) diferenciran po (a; b). Ako u svim točkama intervala (a; b) drugi izvod funkcije y = f(x) negativan, tj. f ""(x) < 0, то график функции на этом интервале выпуклый, если же f""(x) > 0 je konkavan.
Dokaz. Pretpostavimo za određenost da f""(x) < 0 и докажем, что график функции будет выпуклым.
Uzmite graf funkcije y = f(x) proizvoljna točka M0 s apscisom x0 Î ( a; b) i povucite kroz točku M0 tangens. Njezina jednadžba. Moramo pokazati da je graf funkcije na (a; b) leži ispod ove tangente, t.j. s istom vrijednošću x krivulja ordinata y = f(x) bit će manji od ordinate tangente.
Dakle, jednadžba krivulje je y = f(x). Označimo tangentnu ordinatu koja odgovara apscisi x. Zatim . Dakle, razlika između ordinata krivulje i tangente na istoj vrijednosti xće .
Razlika f(x) – f(x0) transformirati prema Lagrangeovom teoremu, gdje je c između x i x0.
Tako,
Ponovno primjenjujemo Lagrangeov teorem na izraz u uglastim zagradama: , gdje c 1 između c 0 i x0. Prema teoremu f ""(x) < 0. Определим знак произведения второго и третьего сомножителей.
Dakle, bilo koja točka krivulje leži ispod tangente na krivulju za sve vrijednosti x i x0 Î ( a; b), što znači da je krivulja konveksna. Slično se dokazuje i drugi dio teorema.
Primjeri.
Točka na grafu kontinuirane funkcije koja odvaja njezin konveksni dio od konkavnog naziva se prevojna točka.
Očito, u točki pregiba, tangenta, ako postoji, siječe krivulju, jer s jedne strane ove točke, krivulja leži ispod tangente, a s druge strane, iznad nje.
Definirajmo dovoljne uvjete da zadana točka krivulje bude točka pregiba.
Teorema. Neka je krivulja definirana jednadžbom y = f(x). Ako je a f ""(x 0) = 0 ili f ""(x 0) ne postoji i prilikom prolaska kroz vrijednost x = x0 izvedenica f ""(x) mijenja predznak, zatim točka grafa funkcije s apscisom x = x0 postoji prijelomna točka.
Dokaz. Neka bude f ""(x) < 0 при x < x0 i f ""(x) > 0 at x > x0. Zatim kod x < x0 krivulja je konveksna, i x > x0- konkavna. Otuda poanta A, koji leži na krivulji, s apscisom x0 postoji prijelomna točka. Slično, možemo razmotriti i drugi slučaj, kada f ""(x) > 0 at x < x0 i f ""(x) < 0 при x > x0.
Dakle, točke pregiba treba tražiti samo među onim točkama u kojima druga derivacija nestaje ili ne postoji.
Primjeri. Odrediti točke pregiba i odrediti intervale konveksnosti i konkavnosti krivulja.
ASIMPTOTE GRAFA FUNKCIJE
Kada istražujete funkciju, važno je utvrditi oblik njezina grafa s neograničenim uklanjanjem točke grafa iz ishodišta.
Posebno je zanimljiv slučaj kada se graf funkcije, kada se njezina varijabla točka udalji u beskonačnost, neograničeno približava određenoj ravnoj crti.
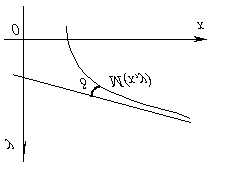
Izravno pozvan asimptota graf funkcije y = f(x) ako je udaljenost od promjenjive točke M graf do ove linije kada se točka ukloni M ka beskonačnosti teži nuli, t.j. točka grafa funkcije, budući da teži beskonačnosti, mora se neograničeno približavati asimptoti.
Krivulja se može približiti svojoj asimptoti, ostajući na jednoj njezinoj strani ili na različitim stranama, sijekući asimptotu beskonačan broj puta i kretajući se s jedne strane na drugu.
Označimo li s d udaljenost od točke M krivulje na asimptotu, jasno je da d teži nuli kako se točka ukloni M do beskonačnosti.
Nadalje ćemo razlikovati vertikalne i kose asimptote.
VERTIKALNE ASIMPTOTE
Neka na x→ x0 obje strane funkcije y = f(x) neograničeno raste u apsolutnoj vrijednosti, t.j. ili ili 
. Tada iz definicije asimptote slijedi da je pravac x = x0 je asimptota. Obrnuto je također očito ako je linija x = x0 je asimptota, dakle .
Dakle, vertikalna asimptota grafa funkcije y = f(x) naziva se linija ako f(x)→ ∞ pod barem jednim od uvjeta x→ x0– 0 ili x → x0 + 0, x = x0
Stoga, pronaći vertikalne asimptote grafa funkcije y = f(x) potrebno je pronaći te vrijednosti x = x0, pri čemu funkcija ide u beskonačnost (trpi beskonačan diskontinuitet). Tada vertikalna asimptota ima jednadžbu x = x0.
Primjeri.
KOSE ASIMPTOTE
Budući da je asimptota ravna linija, onda ako je krivulja y = f(x) ima kosu asimptotu, tada će njena jednadžba biti y = kx + b. Naš zadatak je pronaći koeficijente k i b.
Teorema. Ravno y = kx + b služi kao kosa asimptota pri x→ +∞ za graf funkcije y
= f(x) ako i samo ako 
. Slična izjava vrijedi za x → –∞.
Dokaz. Neka bude MP- duljina segmenta jednaka udaljenosti od točke M na asimptotu. Po uvjetu. Označimo s φ kut nagiba asimptote prema osi Vol. Zatim od ΔMNP slijedi da . Budući da je φ konstantan kut (φ ≠ π/2), onda , ali
Uputa
Točke pregiba funkcije moraju pripadati domeni njezine definicije, koja se mora prvo pronaći. Funkcijski graf je linija koja može biti kontinuirana ili imati lomove, monotono se smanjivati ili povećavati, imati minimalne ili maksimalne točke (asimptote), biti konveksna ili konkavna. Oštra promjena u posljednja dva stanja naziva se infleksija.
Nužan uvjet za postojanje fleksije funkcije je da je sekunda jednaka nuli. Dakle, diferenciranjem funkcije dvaput i izjednačavanjem rezultirajućeg izraza s nulom, može se pronaći apscisa mogućih točaka fleksije.
Ovaj uvjet proizlazi iz definicije svojstava konveksnosti i konkavnosti grafa funkcije, t.j. negativne i pozitivne vrijednosti druge derivacije. U točki pregiba dolazi do nagle promjene ovih svojstava, što znači da derivacija prelazi nultu oznaku. Međutim, jednakost nuli još uvijek nije dovoljna za označavanje točke infleksije.
Postoje dva dovoljna uvjeta da apscisa pronađena u prethodnoj fazi pripada točki pregiba: Kroz ovu točku možete povući tangentu na funkciju. Druga derivacija ima različite predznake desno i lijevo od navodne točke pregiba. Dakle, njeno postojanje u samoj točki nije nužno, dovoljno je utvrditi da u njoj mijenja predznak.Drugi izvod funkcije je nula, a treći nije.
Prvi dovoljan uvjet je univerzalan i koristi se češće od ostalih. Razmotrimo ilustrativni primjer: y = (3 x + 3) ∛ (x - 5).
Rješenje. Pronađite domenu definicije. U ovom slučaju nema ograničenja, dakle, to je cijeli prostor realnih brojeva. Izračunajte prvi izvod: y' = 3 ∛ (x - 5) + (3 x + 3) / ∛ (x - 5)².
Obratite pažnju na izgled razlomka. Iz ovoga proizlazi da je područje definicije izvedenice ograničeno. Točka x = 5 je probušena, što znači da kroz nju može proći tangenta, što dijelom odgovara prvom kriteriju za dovoljnost infleksije.
Odredite jednostrane granice za rezultirajući izraz pri x → 5 - 0 i x → 5 + 0. One su jednake -∞ i +∞. Dokazali ste da okomita tangenta prolazi točkom x=5. Ova točka može biti točka pregiba, ali prvo izračunajte drugi izvod: - 5)^5 = (2 x - 22)/∛(x - 5)^5.
Izostavite nazivnik, jer ste već uzeli u obzir točku x = 5. Riješite jednadžbu 2 x - 22 = 0. Ima jedan korijen x = 11. Posljednji korak je potvrditi da su točke x = 5 i x = 11 prevojne točke. Analizirati ponašanje druge derivacije u njihovoj blizini. Očito, u točki x = 5 mijenja predznak iz “+” u “-”, au točki x = 11, obrnuto. Zaključak: obje točke su točke pregiba. Prvi dovoljan uvjet je zadovoljen.
Pomoću online kalkulatora možete pronaći točke pregiba i intervali konveksnosti funkcijskog grafa s dizajnom rješenja u Wordu. Je li funkcija dviju varijabli f(x1,x2) konveksna odlučuje se pomoću Hessian matrice.
Pravila unosa funkcije:
Smjer konveksnosti grafa funkcije. Pregibne točke
Definicija: Krivulja y=f(x) naziva se prema dolje konveksna u intervalu (a; b) ako leži iznad tangente u bilo kojoj točki ovog intervala.Definicija: Krivulja y=f(x) naziva se konveksna prema gore u intervalu (a; b) ako leži ispod tangente u bilo kojoj točki ovog intervala. 
Definicija: Intervali u kojima je graf funkcije konveksan prema gore ili prema dolje nazivaju se intervali konveksnosti grafa funkcije.
Konveksnost prema dolje ili prema gore krivulje, koja je graf funkcije y=f(x) , karakterizira predznak njezine druge derivacije: ako je u nekom intervalu f''(x) > 0, tada je krivulja konveksna prema dolje na ovom intervalu; ako je f''(x)< 0, то кривая выпукла вверх на этом промежутке.
Definicija: Točka grafa funkcije y=f(x) koja razdvaja intervale konveksnosti suprotnih smjerova ovog grafa naziva se točka pregiba. 
Samo kritične točke druge vrste mogu poslužiti kao prelomne točke; točke koje pripadaju domeni funkcije y = f(x) , na kojima drugi izvod f''(x) nestaje ili se prekida.
Pravilo za pronalaženje prevojnih točaka grafa funkcije y = f(x)
- Pronađite drugi izvod f''(x) .
- Pronađite kritične točke druge vrste funkcije y=f(x) , tj. točka u kojoj f''(x) nestaje ili se prekida.
- Istražite predznak druge derivacije f''(x) u intervalima na koje pronađene kritične točke dijele domenu funkcije f(x) . Ako, u ovom slučaju, kritična točka x 0 odvaja intervale konveksnosti suprotnih smjerova, tada je x 0 apscisa točke infleksije grafa funkcije.
- Izračunajte vrijednosti funkcije u točkama pregiba.
Primjer 1 . Nađite konveksne praznine i točke pregiba sljedeće krivulje: f(x) = 6x 2 –x 3 .
Rješenje: Pronađite f '(x) = 12x - 3x 2 , f ''(x) = 12 - 6x.
Nađimo kritične točke po drugom izvodu rješavanjem jednadžbe 12-6x=0 . x=2 . 
f(2) = 6*2 2 - 2 3 = 16
Odgovor: Funkcija je konveksna prema gore za x∈(2; +∞) ; funkcija je konveksna prema dolje za x∈(-∞; 2) ; točka pregiba (2;16) .
Primjer 2 . Ima li funkcija točke pregiba: f(x)=x 3 -6x 2 +2x-1
Primjer 3 . Pronađite intervale u kojima je graf funkcije konveksan i konveksan: f(x)=x 3 -6x 2 +12x+4
Za određivanje konveksnosti (konkavnosti) funkcije na određenom intervalu mogu se koristiti sljedeći teoremi.
Teorem 1. Neka je funkcija definirana i kontinuirana na intervalu i ima konačan izvod . Da bi funkcija bila konveksna (konkavna) u , potrebno je i dovoljno da se njezina derivacija smanjuje (povećava) na ovom intervalu.
Teorem 2. Neka funkcija biti definirana i kontinuirana zajedno sa svojim derivacijom na i imati kontinuirani drugi izvod unutar . Za konveksnost (konkavnost) funkcije u potrebno je i dovoljno da unutra
Dokažimo teorem 2 za slučaj konveksnosti funkcije.
Potreba. Uzmimo proizvoljnu točku. Proširujemo funkciju blizu točke u Taylorov niz
Jednadžba tangente na krivulju u točki koja ima apscisu:
Tada je višak krivulje nad tangentom na nju u točki jednak
Dakle, ostatak je jednak višku krivulje nad tangentom na nju u točki . Zbog kontinuiteta, ako 
, Zatim i za , Pripada dovoljno malom susjedstvu točke , i stoga, očito, za bilo koji različit od vrijednosti , Pripada naznačenom susjedstvu.
To znači da graf funkcije leži iznad tangente i da je krivulja konveksna u proizvoljnoj točki.
Adekvatnost. Neka je krivulja konveksna na intervalu . Uzmimo proizvoljnu točku.
Slično prethodnom, proširujemo funkciju blizu točke u Taylorov niz
Višak krivulje nad tangentom na nju u točki koja ima apscisu, definiran izrazom, jednak je
Budući da je višak pozitivan za dovoljno malo susjedstvo točke , druga derivacija je također pozitivna. Dok težimo, dobivamo to za proizvoljnu točku .
Primjer. Istražite funkciju konveksnosti (konkavnosti) .
Njegov derivat 
raste na cijeloj realnoj osi, pa je po teoremu 1 funkcija konkavna na .
Njegov drugi derivat 
, dakle, prema teoremu 2, funkcija je konkavna na .
3.4.2.2 Prevojne točke
Definicija. prevojna točka graf neprekidne funkcije naziva se točka koja razdvaja intervale u kojima je funkcija konveksna i konkavna.
Iz ove definicije proizlazi da su točke pregiba točke ekstremne točke prve derivacije. To podrazumijeva sljedeće tvrdnje za potrebne i dovoljne uvjete pregiba.
Teorem (nužni uvjet pregiba). Da bi točka bila prijelomna točka dvostruko diferencibilne funkcije, potrebno je da njezina druga derivacija u ovoj točki bude jednaka nuli ( 
) ili nije postojao.
Teorem (dovoljan uvjet za fleksiju). Ako drugi izvod dvostruko diferencibilne funkcije promijeni predznak kada prolazi kroz određenu točku, tada postoji točka pregiba.
Imajte na umu da druga derivacija možda ne postoji u samoj točki.
Geometrijska interpretacija točaka pregiba ilustrirana je na sl. 3.9
U susjedstvu točke, funkcija je konveksna i njezin graf leži ispod tangente nacrtane u ovoj točki. U susjedstvu točke, funkcija je konkavna i njezin graf leži iznad tangente nacrtane u ovoj točki. U točki pregiba tangenta dijeli graf funkcije na područja konveksnosti i konkavnosti.
3.4.2.3 Ispitivanje funkcije za konveksnost i prisutnost točaka pregiba
1. Pronađite drugu izvedenicu.
2. Pronađite točke u kojima druga derivacija ili ne postoji.
Riža. 3.9.
3. Ispitati predznak druge derivacije lijevo i desno od pronađenih točaka i zaključiti o intervalima konveksnosti ili konkavnosti i prisutnosti prevojnih točaka.
Primjer. Istražite funkciju za konveksnost i prisutnost točaka pregiba.
2. Drugi izvod jednak je nuli na .
3. Druga derivacija mijenja predznak na , tako da je točka točka pregiba.
Na intervalu , tada je funkcija konveksna na ovom intervalu.
Na intervalu , tada je funkcija konkavna na ovom intervalu.
3.4.2.4 Opća shema za proučavanje funkcija i crtanje
Prilikom proučavanja funkcije i crtanja njezina grafa, preporuča se koristiti sljedeću shemu:
- Pronađite opseg funkcije.
- Istražite funkciju za paran - neparan. Podsjetimo da je graf parne funkcije simetričan oko y-osi, a graf neparne funkcije simetričan je u odnosu na ishodište.
- Pronađite vertikalne asimptote.
- Istražite ponašanje funkcije u beskonačnosti, pronađite horizontalne ili kose asimptote.
- Naći ekstreme i intervale monotonosti funkcije.
- Nađite intervale konveksnosti funkcije i točke pregiba.
- Pronađite točke presjeka s koordinatnim osi.
Proučavanje funkcije provodi se istodobno s konstrukcijom njezina grafa.
Primjer. Istražite funkciju 
i zacrtaj ga.
1. Opseg funkcije - .
2. Funkcija koja se proučava je parna 
, pa je njegov graf simetričan u odnosu na y-os.
3. Nazivnik funkcije nestaje na , Tako da graf funkcije ima vertikalne asimptote i .
Točke su točke diskontinuiteta druge vrste, budući da granice s lijeve i desne strane na tim točkama teže .
4. Ponašanje funkcije u beskonačnosti.
Stoga graf funkcije ima horizontalnu asimptotu.
5. Ekstremi i intervali monotonosti. Pronalaženje prve izvedenice
Za , Dakle, funkcija opada u tim intervalima.
Za , Dakle, funkcija raste u tim intervalima.
Za , Dakle, točka je kritična točka.
Pronalaženje druge derivacije
Budući da je , tada je točka minimalna točka funkcije .
6. Intervali konveksnosti i točke pregiba.
Funkcija na 
, pa je funkcija konkavna na ovom intervalu.
Funkcija na , znači da je funkcija konveksna na tim intervalima.
Funkcija nikada ne nestaje, tako da nema infleksnih točaka.
7. Točke sjecišta s koordinatnim osovinama.
Jednadžba , ima rješenje , što znači točku presjeka grafa funkcije s y-osi (0, 1).
Jednadžba nema rješenja, što znači da nema točaka presjeka s osi apscise.
Uzimajući u obzir provedeno istraživanje, moguće je izgraditi graf funkcije
Shematski graf funkcije 
prikazano na sl. 3.10.
Riža. 3.10.
3.4.2.5 Asimptote grafa funkcije
Definicija. Asimptota graf funkcije naziva se ravna linija, koja ima svojstvo da udaljenost od točke () do ove ravne crte teži 0 uz neograničeno uklanjanje točke grafa od ishodišta.
